Веснина А.А., Стругова Т.М. Методические указания и контрольные задания (с примерами решения) Часть 1
Подождите немного. Документ загружается.


1. а)
2
1
3
yx
zyx
zyx
б)
6133
34
053
332
zyx
zyx
zyx
zyx
в)
1
1
3
yx
zyx
zyx
г)
2749
42253
6372
tzyx
tzyx
tzyx
2. а)
510114
3432
2
zyx
zyx
zyx
б)
1151132
23264
17532
tzyx
tzyx
tzyx
в)
2963
3642
132
zyx
zyx
zyx
г)
1278
7532
9934
8852
zyx
zyx
zyx
zyx
3. а)
3963
2642
132
zyx
zyx
zyx
б)
6563
52
32
6
zyx
zyx
zyx
zyx
в)
13
3642
432
zyx
zyx
zyx
г)
2255
123
132
zyx
tzyx
tzyx
4. а)
7233
32
432
zyx
zyx
zyx
б)
13103129
75286
3243
tzyx
tzyx
tzyx
в)
75
2
1
zyx
zyx
zyx
г)
14332
75
53
22
zyx
zyx
zyx
zyx
5. а)
114
332
42
zyx
zyx
zyx
б)
0343
23
0
232
zyx
zyx
zyx
zyx
в)
10233
32
432
zyx
zyx
zyx
г)
1
5432
tzyx
tzyx
6. а)
6133
053
332
zyx
zyx
zyx
б)
42369
33446
24523
tzyx
tzyx
tzyx
в)
3171211
243
12
zyx
zyx
zyx
г)
1278
7532
9934
8852
zyx
zyx
zyx
zyx
7. а)
81555
732
562
zyx
zyx
zyx
б)
6563
52
32
6
zyx
zyx
zyx
zyx
в)
574
453
932
zyx
zyx
zyx
г)
1
5432
tzyx
tzyx
8.а)
510114
3432
2
zyx
zyx
zyx
б)
1343132
0532
13961711
uzyx
uzyx
uzyx
в)
36475
5347
24253
tzyx
tyx
tzyx
г)
12
15423
133
02
zyx
zyx
zyx
zyx
9. а)
543
13
32
zyx
zyx
zyx
б)
552
12
12
tzyx
tzyx
tzyx
в)
36475
5347
24253
tzyx
tzyx
tzyx
г)
12
15423
02
133
zyx
zyx
zyx
zyx
10.а)
8155
162
732
zyx
zyx
zyx
б)
14332
75
53
22
zyx
zyx
zyx
zyx
в)
1875
743
523
zyx
zyx
zyx
г)
18311424
7436
5732
tzyx
tzyx
tzyx
11.а)
4225
2423
132
zyx
zyx
zyx
б)
1278
7532
9934
8852
zyx
zyx
zyx
zyx
в)
15102
13411
1
zyx
zyx
zyx
г)
81433
5326
46539
tzyx
tzyx
tzyx
11

12. а)
1252
523
732
zyx
zyx
zyx
б)
138
123
71112
467
zyx
zyx
zyx
zyx
в)
0343
62
143
zyx
zyx
zyx
г)
6393
284
262
423
zyx
zyx
zyx
zyx
13. а)
7233
32
432
zyx
zyx
zyx
б)
42369
33446
24523
tzyx
tzyx
tzyx
в)
153
432
522
zyx
zyx
zyx
г)
0343
23
0
232
zyx
zyx
zyx
zyx
14.а)
2345
5567
123
zyx
zyx
zyx
б)
1151132
23264
17532
tzyx
tzyx
tzyx
в)
5883
1572
03
zyx
zyx
zyx
г)
1
5432
tzyx
tzyx
15. а)
1252
523
732
zyx
zyx
zyx
б)
2255
123
132
zyx
tzyx
tzyx
в)
143
122
122
zyx
zyx
zyx
г)
6563
52
32
6
zyx
zyx
zyx
zyx
16. а)
543
13
32
zyx
zyx
zyx
б)
14332
75
53
22
zyx
zyx
zyx
zyx
в)
143
422
222
zyx
zyx
zyx
г)
81433
5326
46539
tzyx
tzyx
tzyx
Задание № 3. Решить системы однородных уравнений:
1. а).
01025
04
0243
zyx
zyx
zyx
б).
034
0352
023
0
yx
zyx
zyx
zyx
2. а).
0963
0642
032
zyx
zyx
zyx
б).
0572
0222
03
tzyx
tzyx
tzyx
3. а).
0983
0552
02
tzyx
tzyx
tzyx
б).
0
032
023
zyx
zyx
zyx
4. а).
03
023
0
yx
zyx
zyx
б).
0225
03
0322
02
zyx
zx
zyx
zyx
5.а).
0555
0444
0
zyx
zyx
zyx
б).
043
023
0
tzyx
tzyx
tzyx
6. а).
0
0532
023
zyx
zyx
zyx
б).
0322
0532
034
tzyx
tzyx
tzyx
7.а).
010114
0432
0
zyx
zyx
zyx
б).
0232
0423
0453
022
zyx
zyx
zyx
zyx
8. а).
0875
0432
0
zyx
zyx
zyx
б).
02369
03446
04523
tzyx
tzyx
tzyx
9.а).
032
0
023
zyx
zyx
zyx
б).
06539
0326
01433
tzyx
tzyx
tzyx
10. а).
0223
0
032
zyx
zyx
zyx
б).
0353
02412
02
tzyx
tzyx
tzyx
11.а).
023
052
032
zyx
zyx
zyx
б).
022
02
02
tzyx
tzyx
tzyx
12. а).
02
092
023
zyx
zyx
zyx
б).
0422
03
022
0
zyx
zyx
zyx
zyx
13.а).
02
025
02
zyx
zyx
zyx
б).
0835
022
0345
tzyx
tzyx
tzyx
14.
а).
0654
0753
042
zyx
zyx
zyx
б).
063
0385
0232
042
zyx
zyx
zyx
zyx
12

15.а).
0692
04
0574
0253
zyx
zyx
zyx
zyx
б).
01055
0422
02
zyx
zyx
zyx
16.а).
0111784
02463
03542
tzyx
tzyx
tzyx
б).
0243
0352
023
zyx
zyx
zyx
Тема 3. ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
Задачи для контрольной работы
ЗАДАНИЕ № 1.Построить графики функций путем сдвигов и деформаций:
1.
3
2
1
x
y
2.
7)1(
3
xy
3.
1)1(
3
2
xy
4.
x
y
2
1
3
5.
228
x
y
6.
2
1
)2lg( xy
7.
1)2(log
3
xy
8.
2)lg( xy
9.
xy 2cos2
10.
xarctgy 22
11.
3
arcsin
xy
12.
1)3sin( xy
13.
1)1( xtgy
14.
2
1
1
x
y
15.
3)1(
3
xy
16.
12
3
x
y
ЗАДАНИЕ № 2. Построение графика функции, заданной несколькими
аналитическими выражениями:
1.
хпри
хприx
xf
,0
,sin
)(
2.
1,2
21,1
2,0
)(
2
хприx
хпри
xпри
xf
3.
41,
1
10,2
0,cos
)(
хесли
x
xесли
хеслиx
xf
4.
2,
21,
10,
)(
xеслие
хеслиe
хеслие
xf
x
ч
5.
2,2
20,0
0,1
)(
хеслих
хесли
хеслиx
xf
6.
1,
1
2
1,
)(
хесли
х
хеслих
xf
7.
4,3
40,1
0,3
)(
хеслих
хеслих
хеслих
xf
8.
3,2
31,2
1,1
)(
2
хеслих
хеслих
хеслих
xf
9.
2,1
20,
0,
)(
2
хеслих
хеслих
хеслих
xf
10.
32,4
21,2
13,
)(
3
хеслих
хеслих
хеслих
xf
11.
2
,
2
2
0,sin
0,
3
)(
хеслиx
хеслиx
хесли
х
xf
12.
4
,1
4
0,
0,1
)(
хесли
хеслиtgx
хеслих
xf
13

13.
2
,
2
2
0,cos
0,2
)(
2
хеслиx
хеслиx
хеслих
xf
14.
1,
1
1,52
)(
хесли
х
хеслих
xf
15.
2,22
20,
0,1
)(
2
хеслих
хеслих
хеслих
xf
16.
1,
10,2
0,sin
)(
хеслих
хеслих
хеслиx
xf
ЗАДАНИЕ № 3. Построить графики функций заданных параметрически:
1.
22
3
at
a
y
tх
2.
20,
sin2
cos3
3
2
t
ty
tx
3.
t
tay
tax
0,
2sin
cos2
2
4.
t
tay
tax
0,
sin2
2sin
2
5.
2
3
4 ty
tx
6.
4
2
6
4
6
t
y
t
x
7.
20,
cos3
sin2
2
3
t
t
tx
8.
1
12
2
ty
ttx
9.
3
2
1
ty
tx
10.
3
2
3
ty
tx
11.
54
2
2
tty
tx
12.
22
,
sin
sin1
2
t
ty
tx
13.
22
,
sin2
sin42
2
t
ty
tx
14.
1
3
ty
tx
15.
2
3
2 ty
tx
16.
3
1
ty
tx
ЗАДАНИЕ № 4. Построить графики функций в полярных координатах:
1.
2sin
2.
3cosa
3.
3sina
4.
)cos1(
a
5.
)sin1(
a
6.
)sin1(
а
7.
a
8.
9.
a
10.
11.
2cos1
12.
2sin2
2
13.
2cos3
2
14.
cossin
15.
sin2
3
16.
cos2
1
Тема 4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИЙ
Задачи для контрольной работы
ЗАДАНИЕ № 1. Вычислить пределы функций:
1. 1)
5
152
2
1
lim
x
xx
x
2)
12
12
2
1
lim
хx
хх
x
3)
3
1
2
3
lim
х
хx
x
4)
2
2
02
)2(
2
lim
х
хx
x
5)
143
23
2
2
1
lim
хх
хx
x
6)
13
32
2
2
lim
хх
хx
x
7)
52
12
3
2
lim
хх
хx
x
8)
ххх
x
3
2
lim
14
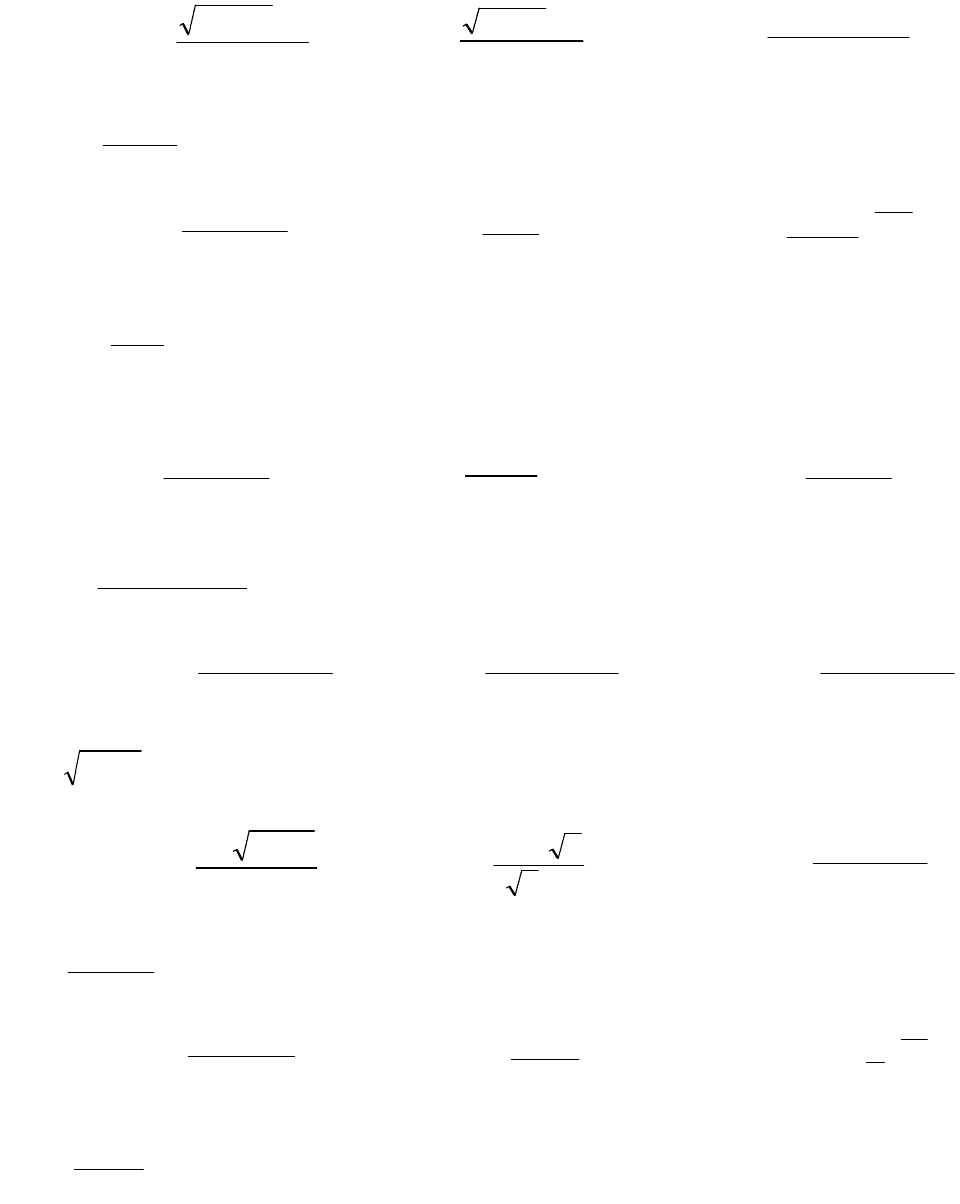
9)
32
2
0
131
lim
хх
х
x
10)
х
х
x
3
116
lim
0
11)
2
3
0
)cos1(4
sin
lim
x
xх
x
12)
xtg
x
x
3
2sin
lim
0
13)
x
x
x
2sin
5arcsin
lim
0
14)
3
1
3
lim
x
x
x
x
15)
5
32
53
43
lim
x
x
x
x
16)
4
1
lim
x
x
x
x
2. 1)
12
5
3
1
lim
х
хx
x
2)
12
2
lim
2
x
x
x
3)
1
3
2
1
lim
х
хx
x
4)
932
2154
2
2
3
lim
хх
хx
x
5)
23
143
2
2
1
lim
хх
хx
x
6)
37
132
2
2
lim
х
хx
x
7)
хх
хx
x
23
172
3
2
lim
8)
24
1
lim
хх
x
9)
2
2
0
11
lim
х
х
x
10)
1
2
1
lim
х
хx
x
11)
3
0
sin
lim
x
xtgx
x
12)
x
xtg
x
15sin
2
lim
0
13)
x
x
x
2arcsin
sin
lim
0
14)
x
x
x
x
2
12
12
lim
15)
3
1
2
1
lim
x
x
x
16)
1
12
32
lim
x
x
x
x
15

3. 1)
3
152
2
1
lim
x
xx
x
2)
1
)2(
2
2
2
lim
хx
x
x
3)
3
2
3
lim
х
хx
x
4)
20
492
2
2
4
lim
хх
хx
x
5)
1572
152
2
2
5
lim
хх
хx
x
6)
52
237
2
2
lim
хх
хx
x
7)
хх
хx
x
2
3
2
12
lim
8)
8
12
2
1
3
2
lim
х
х
x
9)
5
5
lim
5
х
хх
x
10)
2
16
2
4
lim
x
x
x
11)
2
3
0
coscos
lim
x
xx
x
12)
x
xtg
x
7sin
2
lim
0
13)
x
x
x
3
2arcsin
lim
0
14)
x
x
x
10
1
lim
15)
2
34
14
lim
x
x
x
x
16)
x
x
x
x
23
43
lim
4. 1)
32
125
2
1
lim
x
xx
x
2)
22
2
2
2
lim
хx
x
x
3)
2
2
3
)3(
32
lim
х
хx
x
4)
82
12
2
2
4
lim
хх
хx
x
5)
65
12
2
2
3
lim
хх
хx
x
6)
хх
хx
x
3
3
4
138
lim
7)
12
13
2
3
lim
х
хx
x
8)
131
lim
0
х
х
x
9)
22
2
0
11
lim
хх
х
x
10)
1
2
1
1
2
1
lim
x
x
x
11)
tgx
x
x
2cos1
lim
0
12)
x
x
x
3sin
4sin
lim
0
16

13)
x
x
x
2
3arcsin
lim
0
14)
x
x
x
2
1
lim
15)
4
1
lim
x
x
x
x
16)
12
2
1
lim
x
x
x
x
5. 1)
12
53
2
2
1
lim
xx
xx
x
2)
25
)2(
2
2
lim
x
x
x
3)
3
1
2
3
lim
х
хx
x
4)
232
65
2
2
2
lim
хх
хx
x
5)
2
2
1
23
2
lim
хх
хx
x
6)
2
17
3
3
lim
х
хx
x
7)
13
12
3
2
lim
хх
x
x
8)
4
4
2
1
2
02
lim
х
х
x
9)
х
хх
x
11
lim
0
10)
33
9
2
3
lim
x
x
x
11)
2
2
0
4
sin
lim
x
x
x
12)
x
x
x
5
cos1
lim
0
13)
x
xtg
x
3
2
lim
0
14)
x
x
x
2
1
1
lim
15)
12
2
5
lim
x
x
x
x
16)
1
52
32
lim
x
x
x
x
6. 1)
32
2
3
1
lim
x
xx
x
2)
1
2
2
2
lim
хx
x
x
3)
3
33
lim
3
х
х
x
4)
14
352
2
2
2
1
lim
х
хx
x
17
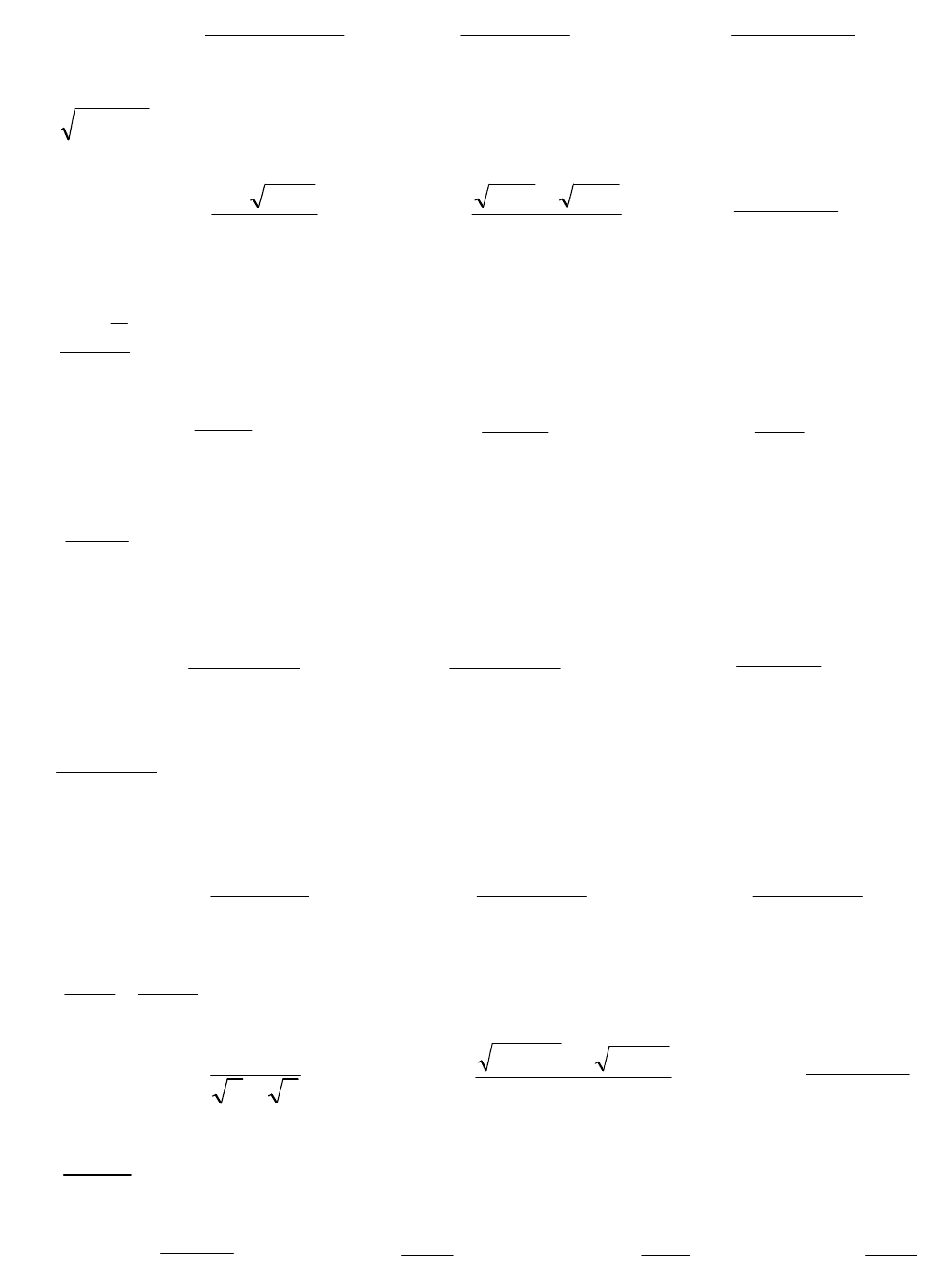
5)
1252
4495
2
2
4
lim
хх
хx
x
6)
53
15
2
2
lim
х
хx
x
7)
32
753
3
2
lim
хх
хx
x
8)
ххх
x
3
2
lim
9)
49
32
2
7
lim
х
х
x
10)
x
xx
x
11
lim
0
11)
2
0
3cos1
lim
x
x
x
12)
2
2
0
2
sin
lim
x
x
x
13)
x
xtg
x
5
3
lim
0
14)
х
x
x
x
32
22
lim
15)
x
x
x
x
1
1
lim
16)
2
2
1
2
2
lim
x
x
x
x
7. 1)
42
35
2
2
1
lim
x
xx
x
2)
22
)2(
2
2
2
lim
хx
x
x
3)
2
2
3
)3(
1
lim
х
x
x
4)
1
2
3
2
1
lim
х
хx
x
5)
хх
хx
x
2
2
2
2
2
lim
6)
52
14
2
2
lim
х
хx
x
7)
65
13
2
3
lim
хх
x
x
8)
8
12
2
1
3
2
lim
х
х
x
9)
2
16
4
2
lim
х
х
x
10)
3
92318
2
3
lim
x
xx
x
11)
xx
x
x
sin
2cos1
lim
0
12)
x
x
x
3sin
lim
0
13)
x
arctgx
x
lim
0
14)
x
x
x
x
4
lim
15)
x
x
x
x
1
lim
16)
x
x
x
x
3
6
lim
18
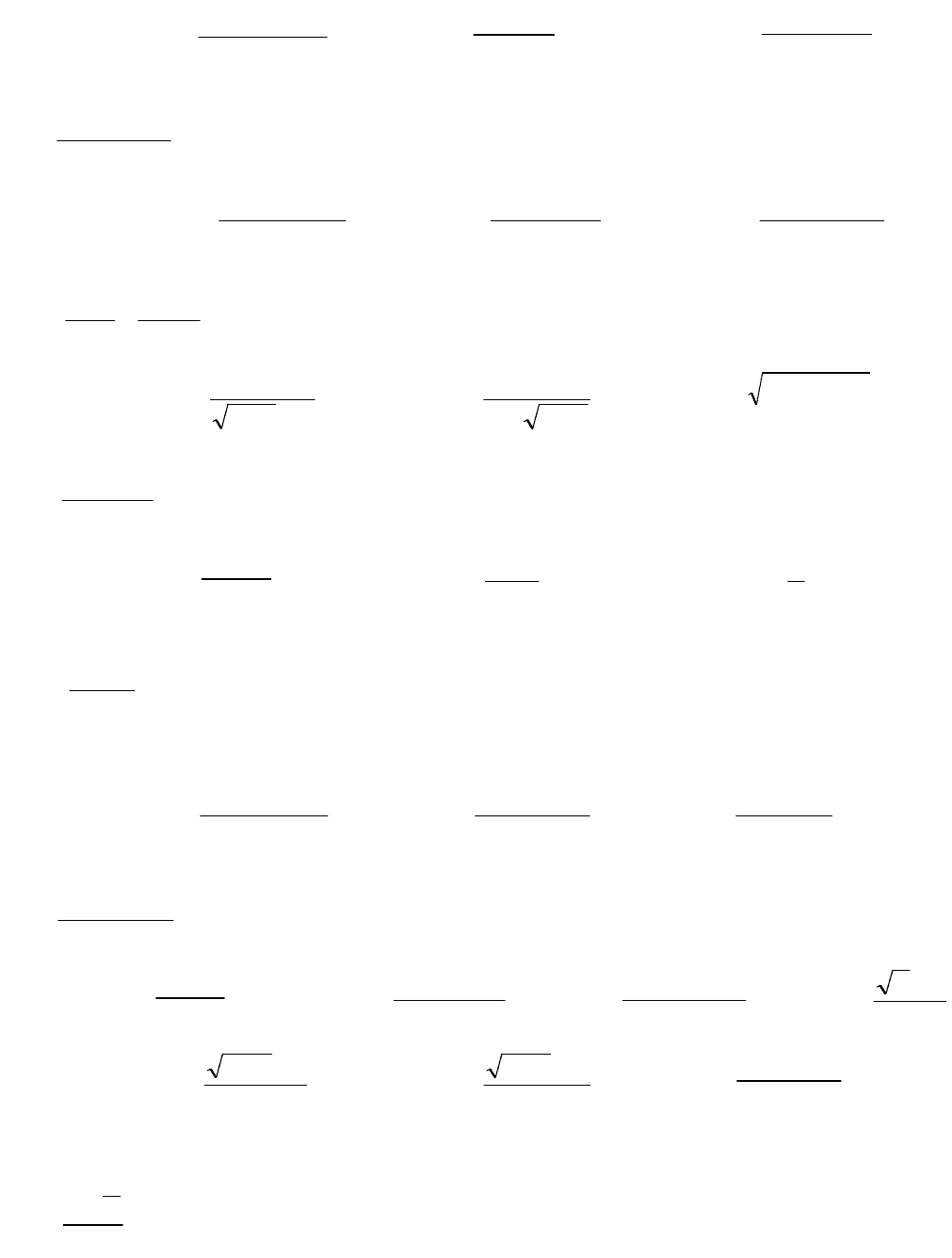
8. 1)
652
743
2
2
2
lim
xx
xx
x
2)
хx
x
x
7
2
2
2
lim
3)
2
2
3
)3(
12
lim
х
хx
x
4)
4
86
2
4
lim
х
хx
x
5)
154
23
2
2
1
lim
хх
хx
x
6)
12
7
2
2
lim
хх
хx
x
7)
1
123
2
4
lim
хх
хx
x
8)
9
6
3
1
2
3
lim
х
х
x
9)
21
9
2
3
lim
х
х
x
10)
12
25
2
5
lim
x
x
x
11)
ххх
x
56
2
lim
12)
x
xarctg
x
5
3
lim
0
13)
x
x
x
2sin
3sin
lim
0
14)
x
x
x
x
3
2
lim
15)
х
x
х
3
1
lim
16)
2
43
12
lim
х
x
x
x
9. 1)
463
254
2
2
2
lim
xx
xx
x
2)
67
45
2
2
4
lim
хx
хx
x
3)
3
1
2
3
lim
х
хx
x
4)
32
9
2
2
3
lim
хх
x
x
5)
8
63
3
2
lim
х
х
x
6)
75
32
2
2
4
lim
хх
хx
x
7)
хх
хx
x
53
178
2
3
lim
8)
1
1
lim
1
х
х
x
9)
2
0
11
lim
х
х
x
10)
5
21
lim
5
x
x
x
11)
xxtg
x
x
2
13cos
lim
0
12)
x
x
x
5
sin
lim
0
19
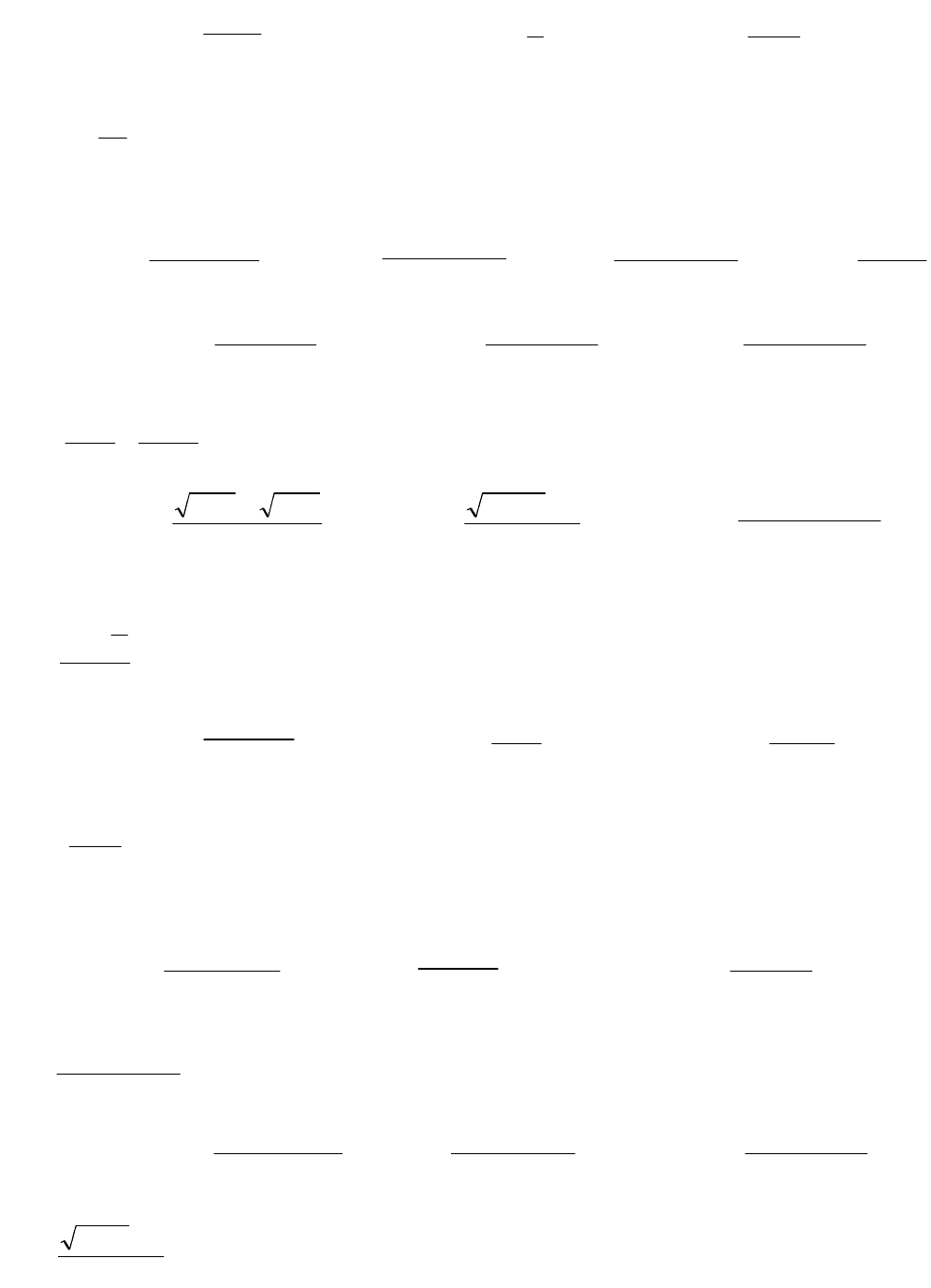
13)
x
xtg
x
2
lim
0
14)
x
x
x
2
1
lim
15)
x
x
x
x
3
1
lim
16)
x
x
x
2
1
1
lim
10. 1)
12
83
2
1
lim
x
xx
x
2)
853
2
2
2
lim
хx
x
x
3)
56
127
2
2
5
lim
хх
хx
x
4)
2
4
2
2
lim
x
x
x
5)
8
2
3
2
2
lim
х
хx
x
6)
7
47
2
2
lim
хх
хx
x
7)
187
1
3
2
lim
хх
хx
x
8)
8
12
2
1
3
2
lim
х
х
x
9)
х
хх
x
11
lim
0
10)
x
x
x
5
117
lim
0
11)
2
0
2coscos
lim
x
xx
x
12)
2
2
0
3
sin
lim
x
x
x
13)
xarctg
x
x
3
lim
0
14)
x
x
x
x
1
1
lim
15)
1
12
32
lim
x
x
x
x
16)
2
3
1
lim
x
x
x
x
11. 1)
32
47
2
1
lim
x
xx
x
2)
хx
x
x
3
2
2
2
lim
3)
3
7
2
3
lim
х
хx
x
4)
67
128
2
2
6
lim
хх
хx
x
5)
654
273
2
2
2
lim
хх
хx
x
6)
хх
хx
x
3
3
4
438
lim
7)
хх
хx
x
7
152
2
3
lim
8)
3
12
lim
3
х
х
x
20
