Васильев В.Г. Критерии качества систем автоматического управления
Подождите немного. Документ загружается.

вычислительная сторона поиска оптимальных настроек регулятора сводится к
следующим основным шагам:
1. Находим передаточную функцию замкнутой системы как функцию
настроечных параметров ПИД- регулятора, т.е поиск минимума
критерия ведем в пространстве трех переменных.
2. По передаточной функции составляем систему дифференциальных
уравнений, описывающих процесс регулирования / управления.
3. Решаем систему дифференциальных уравнений одним из известных нам
методов.
4. Находим значение критерия
J
эт
=
∫
∞
0
δ
2
(t)dt =
∫
∞
0
[ у
эт
(t) – y(t)]
2
dt
5. Сравниваем величину J
эт
со значением критерия, полученным при
выбранных параметрах ПИД- регулятора - K
p,
K
i
K
d.
на предыдущем шаге.
6. Если значение критерия окажется меньше, то параметры Kp, Ki K
d
запоминаются как потенциально оптимальные по выбранному критерию. В
противном случае меняем настройки регулятора и вычислительный процесс
повторяем с шага 3.
В рассмотренном алгоритме можно выделить три ключевых и сложных с
вычислительной стороны пункта:
1) расчет переходного процесса в системе;
2) оценка ее устойчивости;
3) и оптимизации критерия.
Рассмотрим подробно последний пункт. Будем полагать, что предельные
настроечные параметры регулятора известны и определяются либо его
конструктивным исполнением, либо исходя из устойчивости системы при этих
значениях. Тогда математически задачу поиска оптимальных настроек
регулятора можно записать виде :
11
-требуется найти
J
эт
=
∫
∞
0
δ
2
(t)dt =
∫
∞
0
[ у
эт
(t) – y(t)]
2
dt -> min
при ограничениях:
0 <= K
p
<= K
p_max
0 <= K
i
<= K
i_max
0 <= K
d
<= K
d_max
где K
p_max ,
K
i_max,
K
d_max
- предельные значения введения в закон
регулирования пропорциональной, интегральной и дифференциальной
составляющих.
Существует большое число эффективных методов поиска экстремума
функции нескольких переменных. Эффективность методов, в основном,
определяется, двумя факторами: временем, затрачиваемым на поиск
экстремума, и обеспечивает ли метод поиск глобального оптимума. Время,
затрачиваемое на решение задачи, имеет критичное значение, если, к примеру,
система управления требует частых перенастроек. Для большинства
технологических процессов этого не требуется. С точки зрения поиска
глобального оптимума самым надежным, но и одновременно самым
медленным, остается метод полного перебора всех переменных с малым шагом.
Для современной вычислительной техники поиск экстремума функции в
пространстве трех переменных с ограничениями типа “ящик” задача вполне
решаема и в обозримое время.
5. Решение контрольных – тестовых примеров
Нами была написана специальная программа в среде C++ Builder, на
которую получено свидетельство об официальной регистрации программы для
ЭВМ. Основное окно программы представляет собой монтажный стол, на
котором конструируется система. В панели «инструментов» программы в
12
представлены основные звенья ТАУ и регулятор. Пользователь стаскивает
звенья с панели и помещает их либо в прямую, либо в обратную связь системы
(рис. 2). Ввод параметров звеньев осуществляется непосредственно на схеме.
При этом автоматически определяется передаточная функция системы.
Одновременно можно исследовать замкнутую и разомкнутую системы.
Рис 2. Структурная схема системы автоматического управления
Работу программы настройки регулятора продемонстрируем на
следующих контрольных примерах.
Система 1. Структурная схема системы представлена на рис. 2. В цепи прямой
связи последовательно включены регулятор и два апериодических звена
первого порядка. Потребуем, чтобы переходный процесс имел апериодический
характер и берем в качестве эталонной кривой зависимость вида
y
эт
(t) = [1 – exp ( - t / T) ] для t >0
где T - постоянная времени, равная 2 с. На рис. 3 эталонная кривая
переходного процесса показана зеленым цветом. В результате моделирования
получено, что при параметрах настройки регулятора: K
p
= 1.0, K
i
= 0.15 и K
d
=2.19 переходный процесс будут протекать по кривой, представленной на рис.
3 красным цветом. Две кривых переходного процесса практически совпали.
13

Рис. 3. Эталонная и расчетная кривая переходного
процесса для системы 1
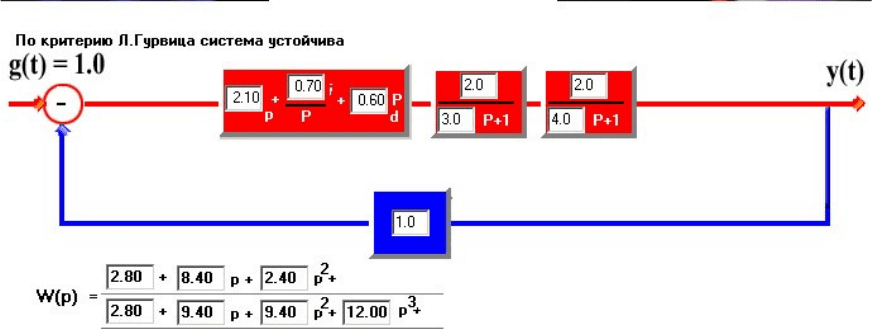
Система 2. Структурная схема системы представлена на рис. 4. В цепи прямой
связи последовательно включены регулятор, колебательное звено и звено
запаздывания. Потребуем, чтобы переходный процесс имел апериодический
вид и выберем в качестве эталонной кривой экспоненту c постоянной времени
1.9 c.
Рис. 4 Структурная схема системы 2
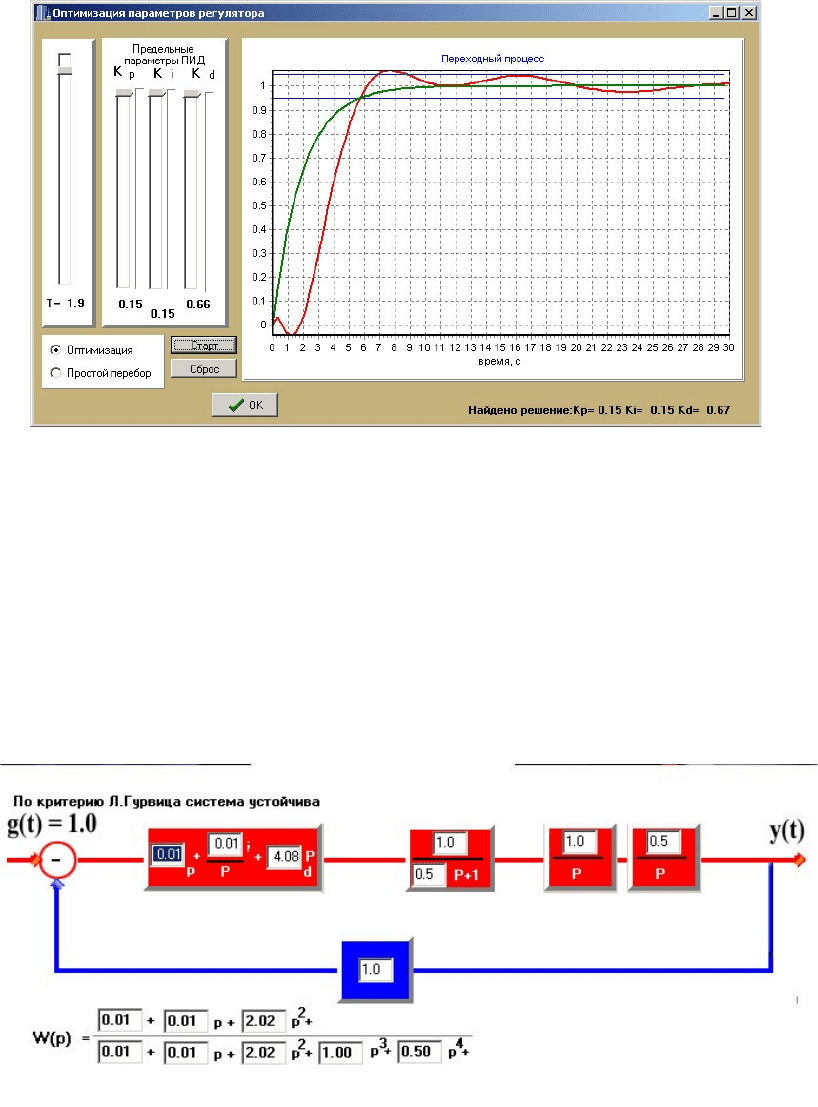
На рис. 5 эталонная кривая переходного процесса показана зеленым цветом. В
результате моделирования получено, что при параметрах настройки
регулятора: K
p
= 0.15, K
i
= 0.15 и K
d
=0.67 переходный процесс будут
протекать по кривой, представленной на рис. 4 красным цветом.
14
Проектируемая система, таким образом, будет иметь переходный процесс по
качеству практически не уступающий эталону ( одинаковое время переходного
процесса и отсутствие перерегулирования).
Рис. 5. Эталонная и расчетная кривая переходного
процесса для системы 2
Система 3. Структурная схема системы представлена на рис. 6.. В цепи прямой
связи последовательно включены регулятор, апериодическое звено и и два
интегрирующих звена. Берем в качестве эталонной кривой экспоненту c
постоянной времени 1 c.
Рис. 6 Структурная схема системы 3
В результате моделирования получено, что при параметрах настройки
регулятора: K
p
= 0.01, K
i
= 0.01 и K
d
=4.0 переходный процесс будут протекать
15
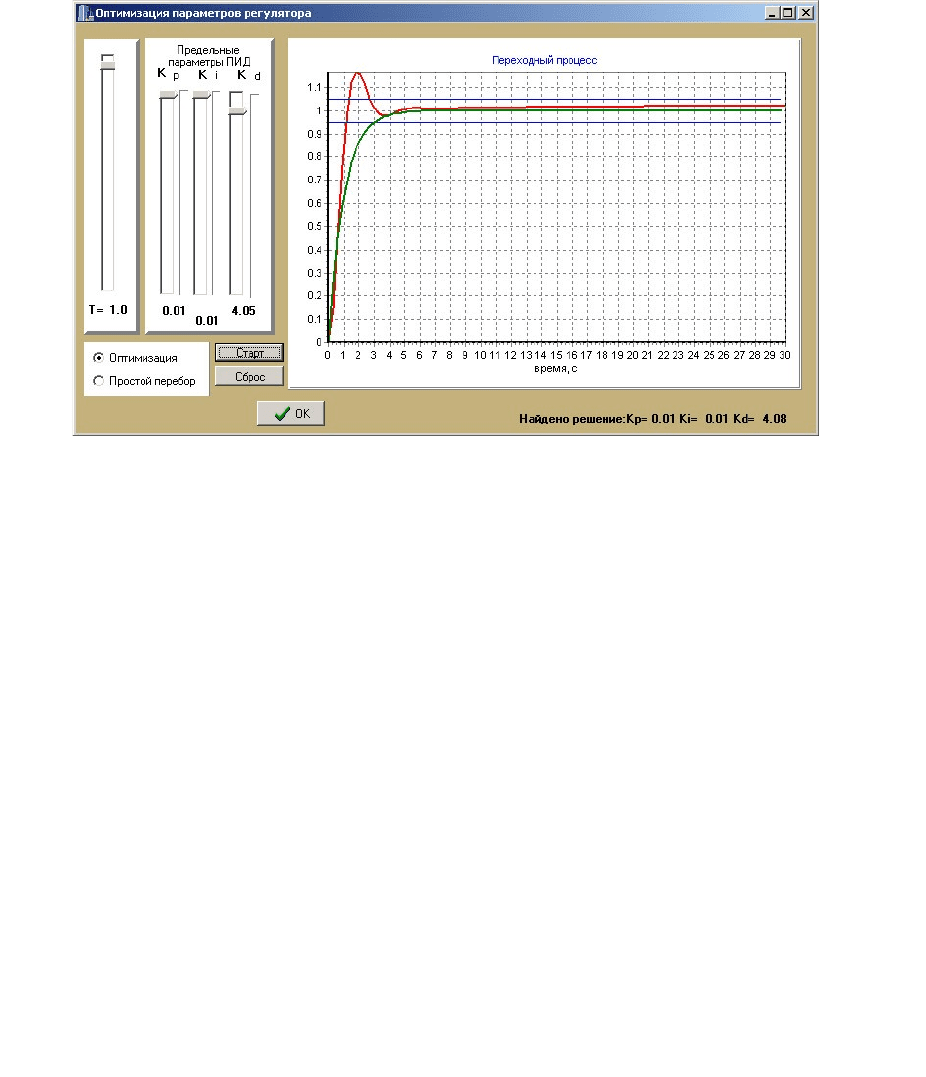
по кривой, представленной на рис. 7 красным цветом. Проектируемая
система, таким образом, будет обеспечивать то же самое время переходного
процесса, но c некоторым перерегулированием.
Рис. 6. Эталонная и расчетная кривая переходного
процесса для системы 1
Таким образом, расчет параметров настройки регулятора по критерию
минимума квадрата отклонения переходного процесса от эталона дает
хорошие результаты для рассмотренных нами систем управления.
Использованная литература
1. Егоров К.В. Основы теории автоматического управления. М.: Энергия,
1967, 648 с.
2. Филлипс Ч., Харбор Р. Системы управления с обратной связью. М.:
Лаборатория базовых знаний, 2001, 615 с.
3. Попов Е.П. Теория линейных систем автоматического регулирования и
управления. - М.: Наука, 1979, 249 с.
4. Г. К. Гудвин , С. Ф. Гребе, М. Э. Сальгадо. Проектирование систем
автоматизации М. «Бином», 2004г.
16

КРИТЕРИИ КАЧЕСТВА СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
для студентов 3 курса спец. 1905500
"Биотехнические и медицинские аппараты и системы"
и для студентов 3 курса спец. 1906600
"Инженерное дело в медико-биологической практике "
по курсу “Управление в медико-биологических системах ”
Составитель В. Г. Васильев
Технический редактор Г.В. Комарова
Подписано в печать 20.12.07
Формат 60 х 84/16 Бумага писчая
Физ.печ.л 1,0 Усл.-печ.л. 0,93 Уч.-изд. л. 0,87
Редакционно-издательский центр
Тверского государственного технического университета
170026, г. Тверь, наб. А. Никитина, 22
17
