Van Kreveld M., Nievergelt J., Roos T., Widmayer P. (eds.) Algorithmic Foundations of Geographic Information Systems

Подождите немного. Документ загружается.

x-queue t

y-table

y 6

1 t

t,i !1

"I I I

-I

t ltl '

III '_

discarded active

tail current

t I

! I

t 1

future

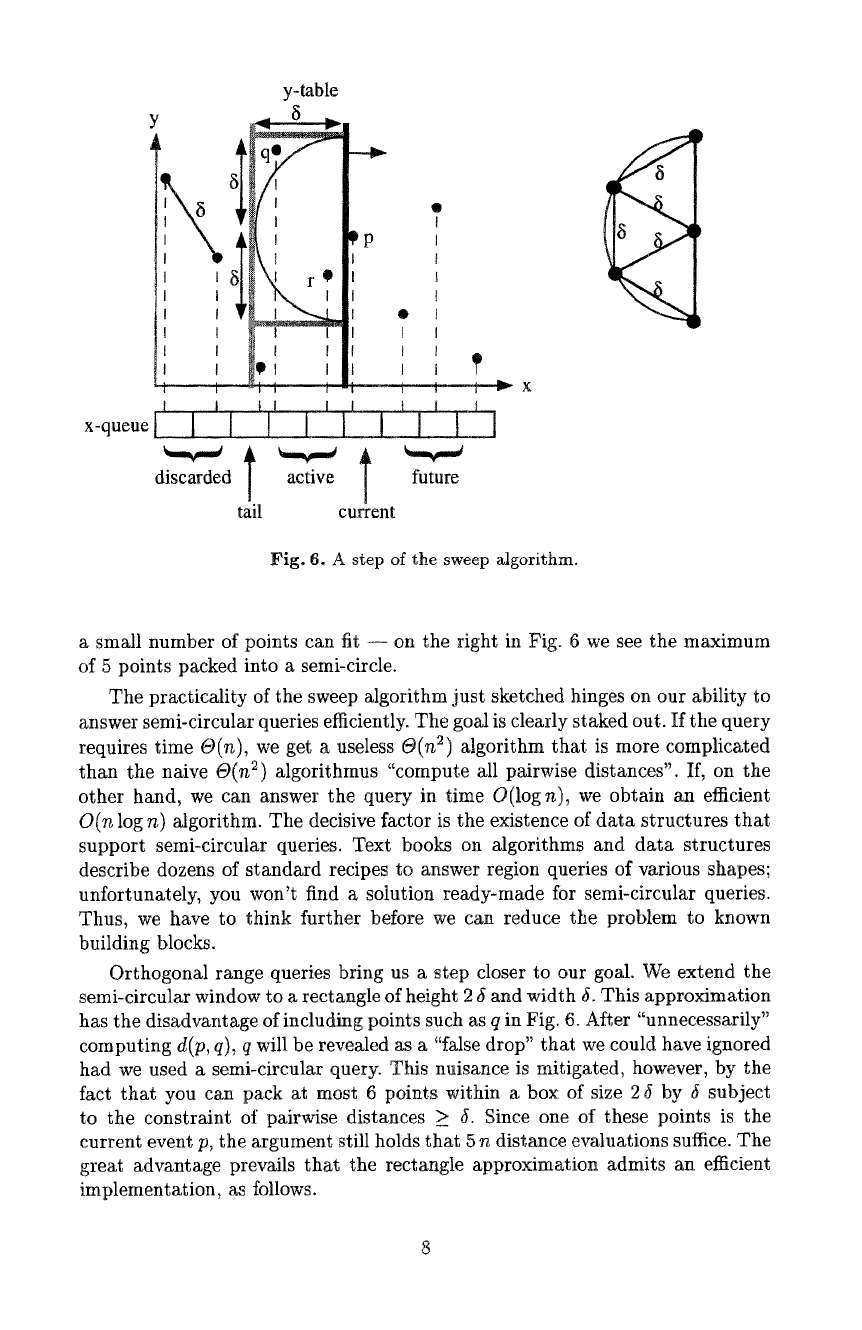
Fig. 6. A step of the sweep algorithm.

a small number of points can fit -- on the right in Fig. 6 we see the maximum

of 5 points packed into a semi-circle.

The practicality of the sweep algorithm just sketched hinges on our ability to

answer semi-circular queries efficiently. The goal is clearly staked out. If the query

requires time O(n), we get a useless O(n 2) algorithm that is more complicated

than the naive O(n 2) algorithmus "compute all pairwise distances". If, on the

other hand, we can answer the query in time O(logn), we obtain an efficient

O(n

log n) algorithm. The decisive factor is the existence of data structures that

support semi-circular queries. Text books on algorithms and data structures

describe dozens of standard recipes to answer region queries of various shapes;

unfortunately, you won't find a solution ready-made for semi-circular queries.

Thus, we have to ~hink further before we can reduce the problem to known

building blocks.

Orthogonal range queries bring us a step closer to our goal. We extend the

semi-circular window to a rectangle of height 2 5 and width 5. This approximation

has the disadvantage of including points such as q in Fig. 6. After "unnecessarily"

computing

d(p, q), q

will be revealed as a "false drop" that we could have ignored

had we used a semi-circular query. This nuisance is mitigated, however, by the

fact that you can pack at most 6 points within a box of size 2 5 by 5 subject

to the constraint of pairwise distances > 5. Since one of these points is the

current event p, the argument still holds that 5 n distance evaluations suffice. The

great advantage prevails that the rectangle approximation admits an efficient

implementation, as follows.

A sweep algorithm maintains a queue of events, in this case the given points,

sorted by x-coordinate. Thus, it is easy to continually discard points that trail

the front by a distance > 5. When answering a query, we consider only the

"active" points, i.e. those that lie in a narrow strip of width ~ to the left of the

front. Depending on where the current event p lies on the front, any of the active

points can form a new closest pair with p. We maintain the active points, sorted

by y-coordinate, in a table that permits fast "dictionary operations": find, insert,

delete, predecessor and successor.

This standard data type "dictionary" can be implemented using a dozen

different data structures, resulting in different performance characteristics. We

aim at an algorithm that runs in time

O(ntogn)

in the worst case. Balanced

trees implement dictionary operations with a worst case time bound of O(log k),

where k is the number of entries in the dictionary -- for our sweep algorithm,

k < n. Predecessor and successor require only time O(1). The asymptotic run-

time analysis that follows does not depend on the specific choice of data structure

but only on the existence of data structures that guarantee a time bound of

O(log n) for each dictionary operation.

The current event p is inserted into the table according to its y-coordinate

p.y.

Vertically, p lies in the middle of the 2 ~-range of the rectangular query.

Starting at p, we scan the active points in the table both upwards, applying the

operation "successor" until we exit from the rectangle at coordinate

p.y

+ 5 ; as

well as downwards, applying "predecessor" until we exit from the rectangle at

p.y - 5.

Thus, we have visited each point q in the rectangle and submitted it to

a distance computation

d(p, q).

The total time required for processing an event

p thus adds up to:

(insert

p) +

(~ of points q in the rectangle) × (predecessor or successor + evaluate

d(p, q)).

Insert requires time O(log n); predecessor, successor and evaluate

d(p, q)

need

time O(1). The number of points in the rectangle is < 5. Thus, processing an

event is dominated by the insertion of p into the dictionary and takes time

O(Iogn). With a total of n events we have found a simple, efficient

O(nlogn)

algorithm for the problem of the closest pair. Assuming that standard operations

such as sorting and dictionary access can be obtained from a program library,

this sweep algorithm takes at most one additional page of source code.

The success of sweep algorithms is due to a clever trick. By treating the x-a~is

as a time-dimension, a 2-d problem is reduced to a sequence of 1-d problems. For

1-d data, i.e. totally ordered domains, we know various efficient data structures.

Thanks to these, sweep algorithms succeed in processing n 1-d problems, each of

which may involve n data items, in time

O(ntogn)

rather than in time O(n2).

Unfortunately, this idea does not generalize efficiently to higher dimensions, tf

we sweep 3-d space with a plane, we transform a 3-d problem into a sequence of

2-d problems. The latter generates queries in a 2-d data space, and for these we

rarely have data structures that answer queries in logarithmic time. We leave

the discussion of spatial data structures to the survey in Chapter

4 Degeneracy, Robustness, and the Quest for Perfection

The above description of the closest-pair sweep ignores a few details. Although

these may appear trivial, a programmer cannot ignore them when aiming at

a robust program, i.e. one that will work correctly for

all

data configurations,

rather then merely for most of them. For example, plane sweep relies strongly

on correctly sorted events. What happens if two or more events have exactly

the same x-cx)ordinate? What ff two points in the input data turn out to have

exactly the same x and y coordinates? Are they one point or two? If we treat

them as two distinct points that happen to coincide, in what order do we process

them? Will the algorithm correctly process a distance 5 -- 0? What happens to

the complexity analysis that relied heavily on the fact that at most 5 points can

be located in a query rectangle of size 2 5 by 5?

The closest pair sweep is such an exceptionally simple algorithm that it can

easily be made immune against such nitpicking questions: events of equal x-

coordinate can be processed in any order, and the algorithm terminates when a

distance (~ = 0 has been computed or all events have been processed.

It came as a surprise, however, that "nitpicking questions" of the type above

pose serious and technically very difficult problems for other geometric algo-

rithms that also appear rather simple. Chapter I0, "Precision and robustness",

treats this topic in depth. Here we merely aim to explain why the full extent of

these difficulties was not recognized at first, and what the core cause of these

difficulties is.

The concept of (small) numerical errors, unavoidable in numerical compu-

tation, has been extensively studied. The overriding concern of traditional nu-

merical analysis is to minimize such errors, to study how they propagate, and to

prove rigorous error bounds. An arsenal of techniques has been developed for this

purpose, such as: using double or variable precision at critical steps; algorithms

that adapt their discretization to the data; forward and backward error analy-

sis; the concept of numerical stability; the distinction between well-conditioned

and ill-conditioned problems, and many more. Thus, one might have expected

that the techniques of error control developed by numerical analysts would ap-

ply to geometric computation as well. But those techniques were developed in

the context of linear algebra and differential equations. They apply only to a

limited extent to geometry, since they fail to address the central issue of correct

geometric computation: topological consistency.

Topological consistency is a concept not commonly encountered in traditional

applications of numerical analysis. It calls for computing certain relations among

the data

exactly,

not merely approximately, in the presence of roundoff and other

errors typical of finite number systems. Let us briefly address the issues: What is

it? Why do we care? What concepts are involved? What questions arise? What

can be achieved, and at what cost?

Everytime an algorithm executes a test, it asks a question about the data

configuration and obtains an answer. The issue arises whether the answers ob-

tained are consistent with each other, i.e. whether they correspond to a possible

data configuration of the type the algorithm is supposed to handle. To under-

stand the problem, think of M. Escher's famous drawings of impossible objects:

each and every local snapshot is realistic by itself; but the way the local scenes

relate to each other turns the aggregate into a picture of a physically impossible

scene. This amusing artistic phenomenon is directly analogous to the problem

of inconsistent answers in geometric computation.

Consider the tantalizing phenomenon of "The Braiding of Floating Point

Lines" (L. Ramshaw). According to Euclid, two distinct straight lines in a plane

intersect in at most one point. In view of roundoff errors, is it not surprising

that several different points might simultaneously satisfy both equations that

define the two lines, suggesting a cluster of intersection points. It is a bit sur-

prising, though, to see that the straight lines y = 4.3

x/8.3

and y = 1.4

x/2.7,

evaluated for various values of x using two decimal digit arithmetic, cross each

other repeatedly as shown in Fig. 7, and as indicated numerically in the following

table:

x 1.78.79.85.86.92.931slope

4.3

x/8.31.39.39.43.43.46.46.5181

1.4 x/2.71.37

.40.40.44.44.48.5185

.48-

.38-

.37-

4.3 x/8.3

1.4 x/2.7

ill ill i Ill if ~ ......... .........

.73 .75 .95 x

Fig. 7. Straight lines confined to gridpoints can alternate repeatedly w.r.t, the relation

The numerical behavior observed, i.e. the repeated alternation of the relation-

ship "above-below" as x grows monotonically, is inconsistent with the geometric

properties of straight lines. Does it matter, given that the computed y-values are

so close to each other?

That depends on what conclusions we draw from a few of these observations.

Assume that, in a visibility computation of what can be seen from above, we

are only interested in the question which of the two lines is above the other

one in some interval of the x-axis. From the observed values at x -- .79 and

x = .85 we might wish to conclude that y = 4.3x/8.3 will be above y =

1.4x/2.7

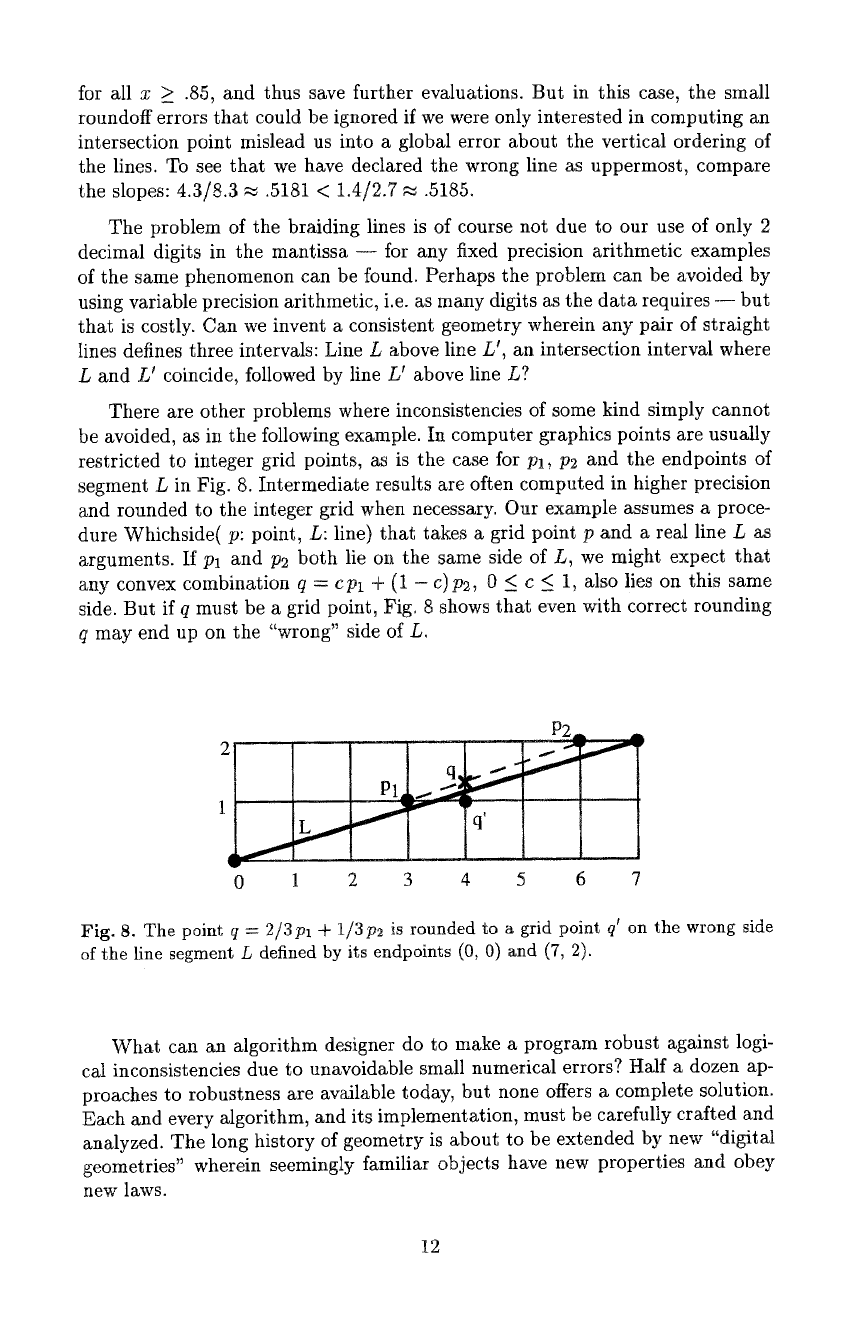
for all x > .85, and thus save further evaluations. But in this case, the small

roundoff errors that could be ignored if we were only interested in computing an

intersection point mislead us into a global error about the vertical ordering of

the lines. To see that we have declared the wrong line as uppermost, compare

the slopes: 4.3/8.3 ~ .5181 < 1.4/2.7 ~ .5185.

The problem of the braiding lines is of course not due to our use of only 2

decimal digits in the mantissa -- for any fixed precision arithmetic examples

of the same phenomenon can be found. Perhaps the problem can be avoided by

using variable precision arithmetic, i.e. as many digits as the data requires -- but

that is costly. Can we invent a consistent geometry wherein any pair of straight

lines defines three intervals: Line L above line L', an intersection interval where

L and L ~ coincide, followed by line L r above line L?

There are other problems where inconsistencies of some kind simply cannot

be avoided, as in the following example. In computer graphics points are usually

restricted to integer grid points, as is the case for Pl, P2 and the endpoints of

segment L in Fig. 8. Intermediate results are often computed in higher precision

and rounded to the integer grid when necessary. Our exa~tpte assumes a proce-

dure Whichside( p: point, L: line) that takes a grid point p and a real line L as

arguments. If Pl and p2 both lie on the same side of L, we might expect that

any convex combination q = cpl + (1 - c)p2, 0 < c < 1, also lies on this same

side. But if q must be a grid point, Fig. 8 shows that even with correct rounding

q may end up on the "wrong" side of L.

1 Pl ,

0 1 2 3 4 5 6 7

Fig. 8. The point q = 2/3pl + 1/3p2 is rounded to a grid point q~ on the wrong side

of the line segment L defined by its endpoints (0, 0) and (7, 2).

What can an algorithm designer do to make a program robust against logi-

cal inconsistencies due to unavoidable small numerical errors? Half a dozen ap-

proaches to robustness are available today, but none offers a complete solution.

Each and every algorithm, and its implementation, must be carefully crafted and

analyzed. The long history of geometry is about to be extended by new "digital

geometries" wherein seemingly familiar objects have new properties and obey

new taws.

5 The XYZ GeoBench: A Program Library for Algorithm

Animation

Computational geometry has now enjoyed two decades of rapid progress. It

turned a field characterized by trial and error into a discipline where no pro-

grammer can work competently in ignorance of theory. But in order to make

the advances of computational geometry accessible to application programmers,

standard algorithms must be turned into correct, robust, efficient, well-tested,

portable programs. It has become clear that the development of professional

software for geometric computation calls for specialists with a broad range of

experience that ranges from algorithm design and analysis to numerics and pro-

gram optimization. Chapter 11, "Implementation and library design of geometric

algorithms", discusses these issues and describes the project CGAL that aims

at a library of production-quality geometric programs.

The implementation of a sophisticated geometric algorithm is an arduous

endeavor if attempted without the right tools, such as: A library of abstract

data types (e.g. dictionary, priority queue) and corresponding data structures

(e.g. balanced tree, heap), reliable geometric primitives (e.g. intersection of 2 line

segments), and visualization aids. What the applications programmer needs, but

can rarely find today, are reliable and efficient reusable software building blocks

that perform the most common geometric operations. Geometric modelers, the

core of CAD systems, do not address this problem -- they are typically monoliths

from which application programmers cannot extract any useful part to use in

their own programs.

In order to provide insight into the functions and structure of a geometry

software system, this section presents an example aimed primarily at educa-

tion. The XYZ (eXperimental geometry Zurich) GeoBench and Program Library

[NSdL+91]is used as a programming environment for rapid prototyping and vi-

sualization of geometric algorithms. The GeoBench is a loosely coupled set of

modules held together by a class hierarchy of geometric objects and common

abstract data types. The program library is a collection of well-tested, practical,

efficient algorithms for basic geometric problems. The XYZ software (written

in Object Pascal for the Macintosh) and documentation is available via anony-

mous ftp from

ftp://ftp.inf.ethz.ch/pub/software/xyz/or

via the World Wide

Web page http://wwwjn.inf.ethz.ch/geobench/XYZGeoBench.html.

5.1 Architecture and Components of the GeoBench

The main goal of the GeoBench and program library is to make available to

the user a loosely coupled collection of carefully crafted software packages that

serve both for the rapid prototyping of new algorithms and for the experimental

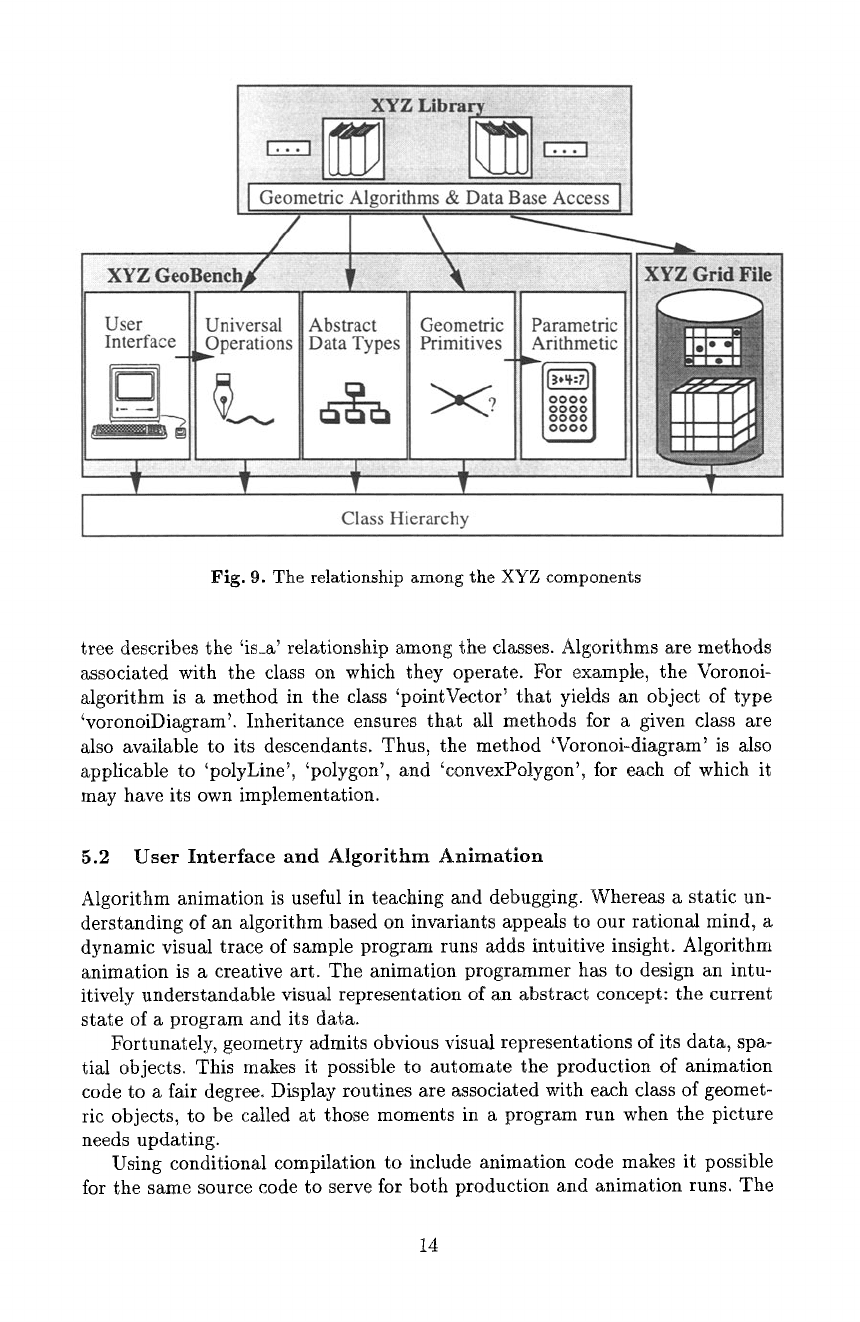
testing and evaluation of existing programs. Fig. 9 presents the structure of this

software system, where an arrow indicates the relationship 'is_based_on'.

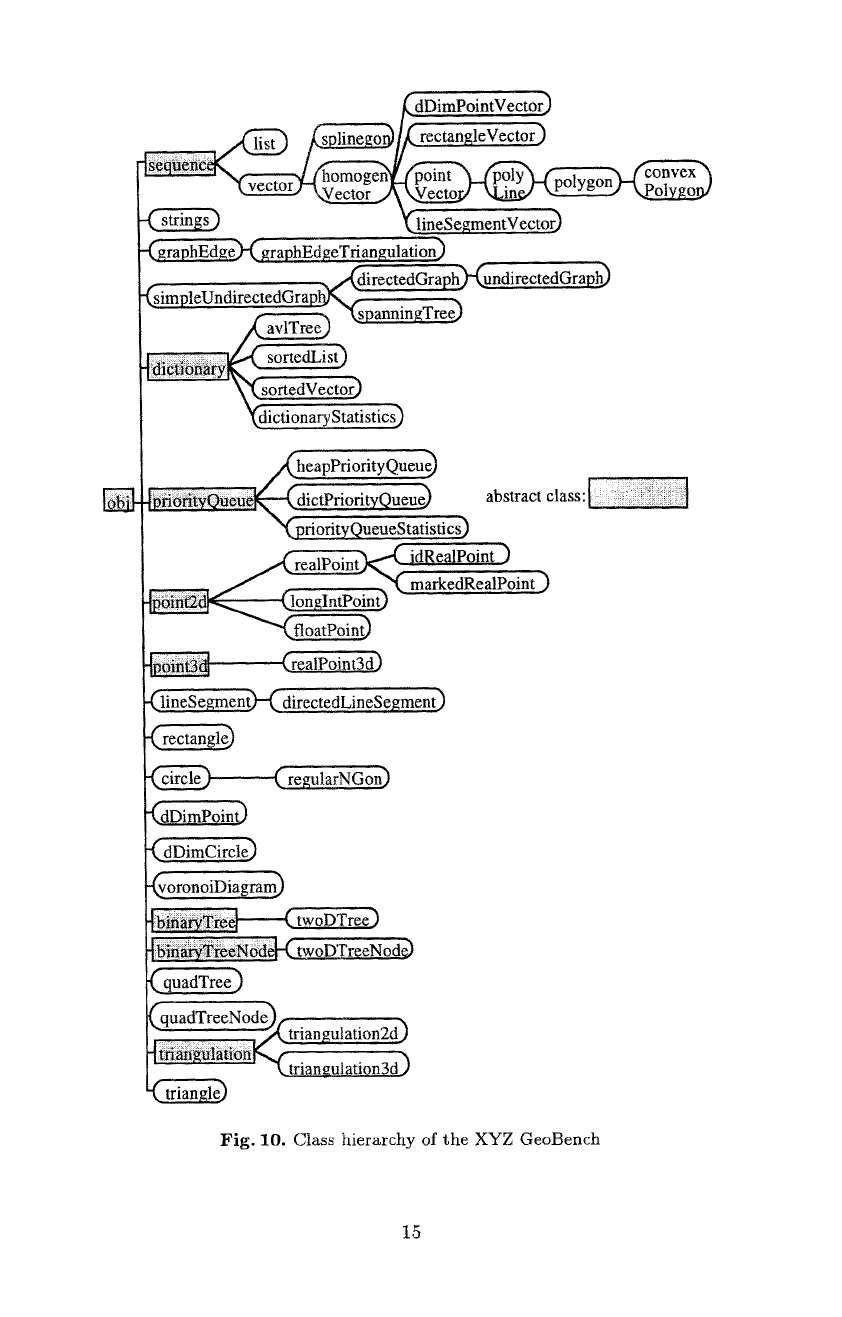
Fig. 10 shows the backbone of the GeoBench. The class hierarchy defines

the common data types and serves as interface between the components. This

...................... ................... .................... .................

User Universal Abstract I Geometric [ Parametric ~t ~ ~!

Interface Operations l Data Types " " '~:4"m' ~'~U Primitives~ Arithmetic ~~

bt) I ~ III ~ ,~ L

ooooi

Class Hierarchy ~]

Fig. 9. The relationship among the XYZ components

tree describes the 'is_a' relationship among the classes. Algorithms are methods

associated with the class on which they operate. For example, the Voronoi-

algorithm is a method in the class 'pointVector' that yields an object of type

'voronoiDiagram'. Inheritance ensures that all methods for a given class are

also available to its descendants. Thus, the method 'Voronoi-diagram' is also

applicable to 'polyLine', 'polygon', and 'convexPolygon', for each of which it

may have its own implementation.

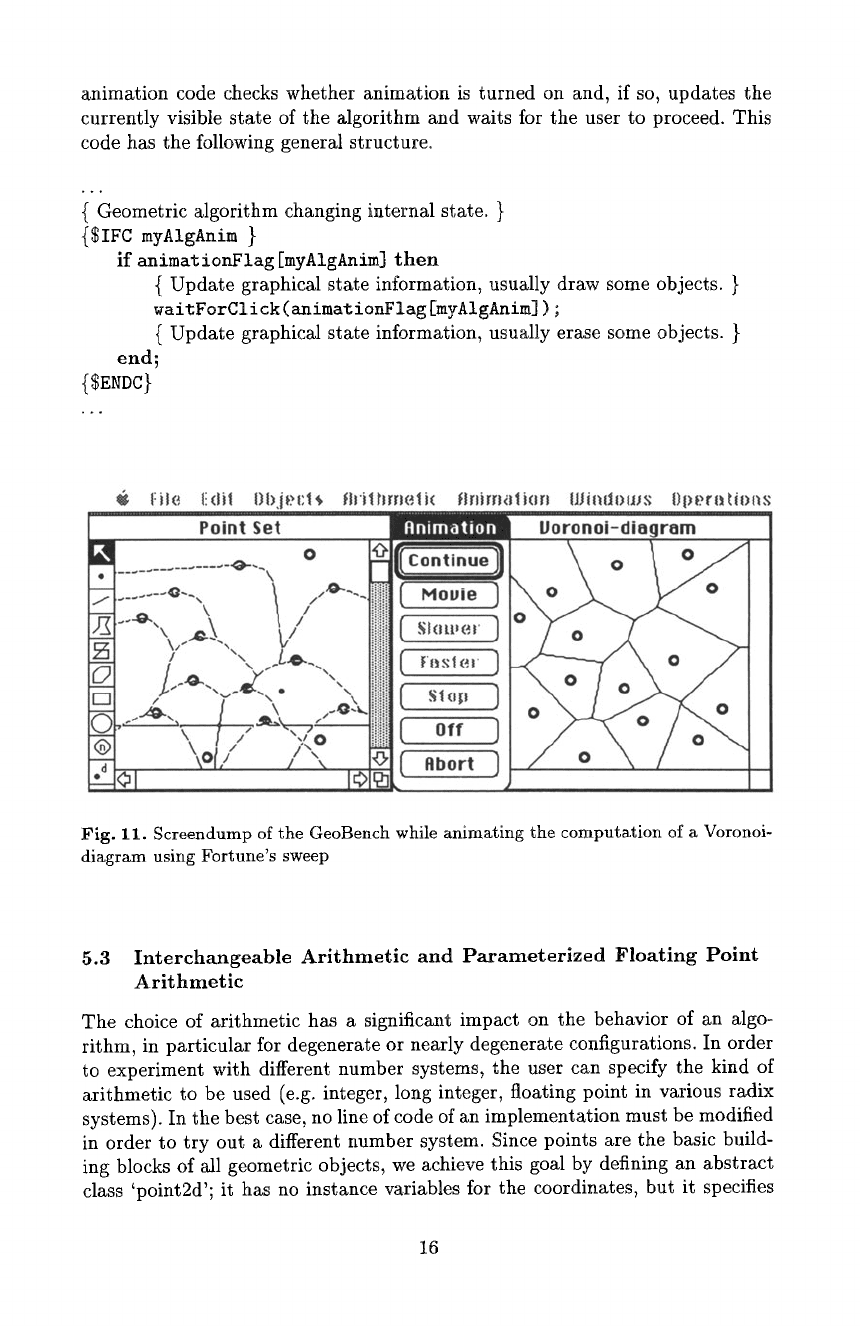
5.2 User Interface and Algorithm Animation

Algorithm animation is useful in teaching and debugging. Whereas a static un-

derstanding of an algorithm based on invariants appeals to our rational mind, a

dynamic visual trace of sample program runs adds intuitive insight. Algorithm

animation is a creative art. The animation programmer has to design an intu-

itively understandable visual representation of an abstract concept: the current

state of a program and its data.

Fortunately, geometry admits obvious visual representations of its data, spa-

tial objects. This makes it possible to automate the production of animation

code to a fair degree. Display routines are associated with each class of geomet-

ric objects, to be called at those moments in a program run when the picture

needs updating.

Using conditional compilation to include animation code makes it possible

for the same source code to serve for both production and animation runs. The

~(,dDimPointVector)

, lineSegmentVector)

"~ralohEd~e)-(gr aphEd~eTriangulation)

.(simpteUndirectedGra'"'ph-~directedGrai h)'(undirectedGraph~

'~spanningTree)

~(dictionaryStatistics)

jJ(rheaPPriorityQueue)

ifi~NtvOueae~-( dictPrioritvoueu'~ abstract

X priorityQueueStatistics~

~ idRealPoint )

nt)" ~ markedRealPoint )

(realPoint3d)

-(lineSegment)-'(directedLineSegment)

(regularNG0n)

"(dDimPoint)

dDimCir ie)

~oronoiDiagram)

tbili Od~twoDTreeNode~

(quadTree)

(quadTreeNode)¢ . ..,

)4, triangu!ation2dj

.... k.triansmation3dJ

Fig. 10. Class hierarchy of the XYZ GeoBench

animation code checks whether animation is turned on and, if so, updates the

currently visible state of the algorithm and waits for the user to proceed. This

code has the following general structure.

{ Geometric algorithm changing internal state. }

{$IFC myAlgAnim }

if animat ionFlag [myAlgAnim] then

{ Update graphical state information, usually draw some objects. }

waitForClick (animationFlag [myAlgAnim] ) ;

{ Update graphical state information, usually erase some objects. }

end;

{$ENDC}

7 ..............

Point Set

r ~

;= . / \

...o.~ ( s~<, )

I@_~ \Or,/ / ", [ Abort )

~'¢'1 , , I¢ ,

liZn~H~Z,[,],i Voronoi-diagram

o-~ o -° ° .......

Fig. 11. Screendump of the GeoBench while animating the computation of a Voronoi-

diagram using Fortune's sweep

5.3 Interchangeable Arithmetic and Parameterized Floating Point

Arithmetic

The choice of arithmetic has a significant impact on the behavior of an algo-

rithm, in particular for degenerate or nearly degenerate configurations. In order

to experiment with different number systems, the user can specify the kind of

arithmetic to be used (e.g. integer, long integer, floating point in various radix

systems). In the best case, no line of code of an implementation must be modified

in order to try out a different number system. Since points are the basic build-

ing blocks of all geometric objects, we achieve this goal by defining an abstract

class 'point2d'; it has no instance variables for the coordinates, but it specifies

an interface that includes access procedures to the coordinates and to various

geometric primitives.

~~ abstract, has no instance variables,

"~interface description

(realPoint) (longIntP'oint) (floatPoint) concrete, has instance variables,

implements required operations

Fig. 12. The abstract class 'point2d' and its descendants

From this abstract 'point2d' we derive concrete point objects with instance

variables and geometric primitives in their respective arithmetic systems. Al-

gorithms that use only the functions and procedures specified by the abstract

type 'point2d' can run in any of the three kinds of arithmetics currently sup-

ported. Whereas 'realPoint' uses the built-in floating point arithmetic, the object

'floatPoint' calls upon a software floating point package that uses any base and

precision specified by the user. The latter can be used both to simulate high

precision arithmetic, as well as low precision in order to accentuate rounding

errors and thus facilitate testing.

5.4 The Program Library: Experimental Performance Evaluation

The XYZ program library contains carefully programmed and tested algorithms

for several dozen standard geometric problems. The presence of several algo-

rithms for solving the same problem reflects our concern for experimental as-

sessment and comparison. As an example, consider the well-known problems of

finding the closest pair and all-nearest-neighbors in a set of n points given in

the plane. These problems date from the early days of computational geome-

try [SH75] and admit several optimal algorithms [PS85]. Convinced that plane-

sweep yields the practically best algorithms for many simple 2-d problems, we

developed new algorithms fbr these well-known problems [HNS92] and compared

them to other algorithms implemented on the GeoBench, using comparable cod-

ing techniques (see also [Sch92]).

As is the case for many proximity problems, closest pair and all-nearest-

neighbors can be solved easily in linear time after the powerful

O(n

log n) prepro-

cessing step of computing the Voronoi diagram. But this diagram contains much

more information than required, and this costs time. Vaidya's box-shrinking

algorithm [Vai89] is another general approach that works in any number of di-

mensions. In contrast, plane-sweep yields direct solutions tailored to 2-d point

proximity problems whose code complexity, memory requirements, and run times

compares favorably with its competitors, as Fig. 13 shows. All algorithms are im-

plemented as part of the XYZ library. The box-shrinking algorithm is optimized

for d = 2; the Voronoi-based algorithm uses the efficient Fortune's sweep [For86].

The graph with logarithmic scales shows run times in seconds for these three