Ухоботов В.И. Математика для экономистов
Подождите немного. Документ загружается.

161
Условия полного дифференциала в этом уравнении выполнены. Запишем
уравнения (3)
−
=
∂
∂
−
=
∂
∂
.
),(
),(
by
m
y
yxu
ax
k
x
yxu
Из первого уравнения находим, что
u
(
x,y
) =
k
ln(
x-a
) +
b
(
y
). Подставим во
второе уравнение получившееся выражение. Получим
).byln(m)y(b
by
m
)y(b
−=⇒
−
=
′
Таким образом, кривые равной полезности задаются уравнениями
k
ln(
x-a
) +
m
ln(
y-b
) =
C=const.
Функция полезности является логарифмической:
u
(
x,y
) =
k
ln(
x-a
) +
m
ln(
y-b
).
Функция полезности
m
)by(
k
)ax(
)y,x(u
e)y,x(v
−−==
является функцией Стоуна.
Тема 31
ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
ВТОРОГО ПОРЯДКА И СИСТЕМА
ИЗ ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Пример. Рассмотрим задачу о спросе и предложении. В реальных условиях
спрос
P
и предложение
Q
в данный момент времени
x
зависят от текущей
цены
y
(
x
) на товар, от ценообразования
y
′
(
x
) и от темпов изменения цены
y
′′
(
x
).
Рассмотрим случай линейной зависимости
Q=L
y
′′
+ A
y
′
+ B y + F,
P=M
y
′′
+ D
y
′
+E y +K .
Требуется установить зависимость цены от времени в условиях равновесного
состояния рынка, которое характеризуется равенством
Q = P
. Отсюда
получим, что
a
0
y
′′
+a
1
y
′
+a
2
y = f
(
x
). (1)
Здесь
a
0
= L – M,
a
1
= A –D , a
2
= B –E, f
(
x
)
= K -F.
Будем рассматривать уравнение (1), у которого все коэффициенты
i
a
являются действительными числами, причем
a
0
≠
0, а функция
f
(
x
)
определена и непрерывна на заданном интервале.
162
Замечание. Уравнение (1) можно рассматривать и в случае, когда все его ко-
эффициенты являются комплексными числами.
Как и в случае квадратного уравнения перейдем к комплексным числам
и будем рассматривать комплекснозначные функции
z(x) = u(x) + i v(x) . (2)
При этом считаем, что k-я производная от комплекснозначной функции оп-
ределяется формулой
)k(
z (x) =
)k(
u
(x) + i
)k(
v
(x) . (3)
При исследовании уравнения (1) существенную роль играет формула Эйлера,
с помощью которой для комплексного числа
λ
=
α
+ i
ω
определяется функ-
ция
xx
ee
αλ
=
(cos
ω
x+i sin
ω
x). (4)
Дифференцируя действительную и мнимую части этой функции, получаем
(e
λ
x
)
′
=
λ
e
λ
x
. (5)
В самом деле,
(e
λ
x
)
′
= (e
α
x
cos
ω
x
)
′
+i(e
α
x
sin
ω
x
)
′
=
=(αe
α
x
cosωx – ωe
α
x
sinωx) + i(αe
α
x
sinωx + ωe
α
x
cosωx)=
=(α+i
ω
) e
α
x
(cos
ω
x + i sin
ω
x).
Вначале рассмотрим уравнение (1), когда в нем в правой части стоит ноль, то
есть
a
0
y
′′
+a
1
y
′
+a
2
y = 0. (6)
Оно называется однородным уравнением. Ищем его решение в виде
y = e
λ
x
. (7)
Число
λ
подлежит определению. Подставим формулы
y = e
λ
x
,
y
′
=
λ
e
λ
x
,
y
′′
=
λ
2
e
λ
x
в уравнение (6). Получим равенство
(a
0
λ
2
+ a
1
λ
+ a
2
) e
λ
x
= 0.
Так как e
λ
x
≠ 0, то из этого равенства следует, что функция (7) является ре-
шением уравнения (6) тогда и только тогда, когда число
λ
является корнем
уравнения
a
0
λ
2
+ a
1
λ
+ a
2
= 0. (8)
Это уравнение называется характеристическим уравнением.
Случай 1. Пусть характеристическое уравнение (8) имеет два различных дей-
ствительных корня λ
1
≠ λ
2.
Тогда общий вид решения уравнения (6) следую-
щий:
xx
ecec)x(y
21
21
λλ
+=
.
Здесь
1
с
и
2
с
– произвольные действительные числа.
Случай 2. Пусть характеристическое уравнение (8) имеет один действитель-
ный корень
λ
. В этом случае общий вид решения ур авнения (6) следующий :
y(x) = (c
1
x + c
2
)
x
e
λ
.
Здесь
1
с
и
2
с
– произвольные действительные числа.
163
Случай 3. Пусть характеристическое уравнение (8) имеет комплексные кор-
ни
λ
1
=
α
+ i
ω
,
λ
2
=
α
– i
ω
. Тогда общий вид решения уравнения (6) следую-
щий:
y(x) = e
α
x
(c
1
cos
ω
x + c
2
sin
ω
x). (9)
Здесь c
1
, c
2
– произвольные действительные числа.
Замечание. Поясним последний случай. В этом случае уравнение (6) будет
иметь комплексное решение
e
λ
x
= e
α
x
(cos
ω
x + i sin
ω
x).
Представим его в виде (2), где
u(x) == e
α
x
cos
ω
x, v(x) = e
α
x
sin
ω
x.
Подставив это комплексное решение в уравнение (6), получим
(a
0
u
′′
+a
1
u
′
+a
2
u) +i(a
0
v
′′
+a
1
v
′
+a
2
v) = 0.
Приравнивая к нулю действительную и мнимую части данного уравнения,
получим, что функции u(x) и v(x) являются решением уравнения (6). Их ли-
нейная комбинация (9) также является решением этого уравнения.
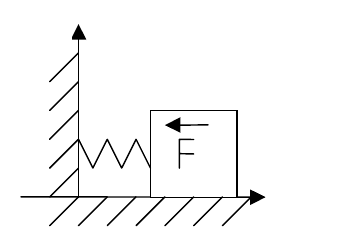
Пример. Пусть тело массой m находится на гладкой плоскости.
Оно прикреплено упругой пружиной к стене.
Обозначим через x(t) расстояние в момент вре-
мени t от тела до стены. По второму закону
Ньютона
m
x
′′
=F.
По закону Гука упругая сила F = -kx. Получим
уравнение
x
′′
+
ω
2
x =0 ,
ω
2
= k/m.
Здесь неизвестной функцией является х(t). Запишем характеристическое
уравнение
λ
2
+
ω
2
= 0.
Это уравнение имеет корни
λ
1
= i
ω
,
λ
2
= -i
ω
. Значит общий вид решения
этого уравнения следующий :
x(t) = c
1
cos
ω
t + c
2
sin
ω
t . (10)
Чтобы найти численные значения постоянных, нужно задать начальное по-
ложение тела x(0)=L и начальную скорость
x
′
(0) = V. Тогда
c
1
cos
ω
0 + c
2
sin
ω
0 = L ⇒ c
1
= L.
Продифференцируем функцию (10) и положим t=0. Получим
-
ω
c
1
sin
ω
0 + c
2
ω
cos
ω
0 = V ⇒
x(t) = Lcos
ω
t + (V/
ω
) sin
ω
t.
Тело совершает колебательные движения с периодом T = (2
π
) /
ω
.
Вернёмся к неоднородному уравнению (1). После того как решено од-
нородное уравнение (6), нужно найти какое-нибудь частное решение уравне-
ния (1) и записать общий вид решения
y
неоднор
(х) = у
однор
(х)+ у
част
(х).
Пример. Рассмотр им предыдущий пример, когда на тело ещё действует сила,
зависящая линейно от времени. Будем иметь уравнение
Y
X

164
x
′′
+
ω
2
x = At + B. (11)
Ищем частное решение в виде многочлена первой степени
x
част
(t) = Dt + P.
Числа D и P подлежат определению. Подставим эту функцию в уравнение
(11). Получим
x
′
част
(t) = D ,
x
′′
част
(t) = 0 =>
ω
2
(Dt + P) = At + B => D = A/
ω
2
, P = B/
ω
2
.
Получим общий вид решения
x(t) = c
1
cos
ω
t + c
2
sin
ω
t + (A/
ω
2
)t + B/
ω
2
.
Замечание. Если функция f(x) является многочленом, то стоит
попытаться искать частное решение в виде многочлена той же самой степе-
ни. Если f(x) = e
bx
, то следует искать решение в виде x
част
(x) = De
bx
, где чис-
ло D подлежит определению.
Система линейных дифференциальных уравнений с постоянными ко-
эффициентами. Такой называется
Здесь a
ij
∈ R являются заданными числами.
Решением называются дифференцируемые функции у
1
(х) и у
2
(х), при под-
становке которых в систему (11) получим тождества.
Ищем решение в следующем виде:
y
1
(x) = e
λ
x
ψ
1
, y
2
(x) = e
λ
x
ψ
2
. (13)
Числа
λ
,
ψ
1
,
ψ
2
подлежат определению. Продифференцируем эти функции и
подставим в систему (1 2). Будем иметь
λ
e
λ
x
ψ
1
= a
11
e
λ
x
ψ
1
+ a
12
e
λ
x
ψ
2,
λ
e
λ
x
ψ
2
= a
21
e
λ
x
ψ
1
+ a
22
e
λ
x
ψ
2.
Сократим эти уравнения на e
λ
x
. Получим
a
11
ψ
1
+ a
12
ψ
2
=
λψ
1
a
21
ψ
1
+ a
22
ψ
2
=
λψ
2.
Таким образом, число
λ
является собственным значением матрицы
=
2221
1211
aa
aa
A
,
а вектор
=
2
1
ψ
ψ
ψ
является ее собственным вектором, отвечающим этому
собственному значению. Для нахождения собственного значения имеем
уравнение
()
.0
211222112211
2
2221
1211
det
=−++−=
−
−
aaaaaa
aa
aa
λλ
λ
λ
)12(.
'
'
2221212
2121111
+=
+=
yayay
yayay

165
Это уравнение называется характеристическим уравнением.
Случай 1. Пусть характеристическое уравнение имеет два различных дейст-
вительных корня. Тогда корням
λ
1
и λ
2
соответствуют собственные вектора
=
12
11
1
ψ
ψ
ψ
,
.
22
21
2
=
ψ
ψ
ψ
Общий вид решений системы (13) в этом случае следующий:
y
1
(x) =
212111
21
ψψ
λλ
xx
ecec
+
y
2
(x) =
222121
21
ψψ
λλ
xx
ecec
+
.
Здесь c
1
и c
2
– произвольные действительные числа.
Случай 2. Пусть характеристическое уравнение имеет один действительный
корень λ.
Случай 2.1. Собственному значению соответствуют два линейно незави-
симых собственных вектора
=
12
11
1
ψ
ψ
ψ
,
.
22
21
2
=
ψ
ψ
ψ
Общий вид решений системы (13) в этом случае следующий:
y
1
(x) =
)(
212111
ψψ
λ
cce
x
+
y
2
(x) =
),(
222121
ψψ
λ
cce
x
+
где c
1
и c
2
– произвольные действительные числа.
Случай 2.2. Собственному значению соответствуют один линейно неза-
висимый собственный вектор
=
2
1
ψ
ψ
ψ
.
Ищем решение в виде
.e)x()x(y,e)x()x(y
xx
λλ
ϕψϕψ
222111
+=+=
Подставим в систему (12). Получим
xxx
e)x(ae)x(ae)x(
λλλ
ϕψϕψλϕψλψ
22121111111
+++=++
xxx
e)x(ae)x(ae)x(
λλλ
ϕψϕψλϕψλψ
22221121222
+++=++
.
Сокращая эти равенства на
x
e
λ
и приравнивая между собой коэффициенты
при соответствующих степенях x, получим
a
11
ϕ
1
+ a
12
ϕ
2
=
ψ
1
+
λϕ
1
a
21
ϕ
1
+ a
22
ϕ
2
=
ψ
2
+
λϕ
2.
Решаем эту систему относительно чисел
ϕ
i.
Общий вид решения в этом слу-
чае следующий:
.Rc,c,e)ccxc()x(y,e)ccxc()x(y
xx
∈∀++=++=
2122212221211121
λλ
ϕψψϕψψ
166
Случай 3. Пусть характеристическое уравнение имеет комплексные корни
λ
1
=
α
+ i
ω
,
λ
2
=
α
– i
ω
. Общий вид решения в этом случае следующий:
),xcos(Ae)x(y
x
γϖ
α
+=
1
.R,A),xsin(Ae)x(y
x
∈∀≥∀+=
γγϖ
α
0
2
Пример. Математическая модель гонки вооружения (модель Ричардсона) .
Имеются две противоборствующие стороны . Пусть у
1
(х) – количество еди-
ниц вооружения первой стороны в момент времени х, а y
2
(х) – количество
единиц вооружения второй стороны в этот момент времени х. Скорость при-
роста количества единиц вооружения у первой стороны пропорциональна
накопленному количеству единиц вооружения второй стороной (чувство
страха) и уменьшается пропорционально накопленному количеству единиц
вооружения самой первой стороной (усталость экономики). Аналогично
для другой стороны. Имеем систему дифференциальных уравнений
−−=
+−=
)(
222
)(
121
)('
2
)(
212
)(
111
)('
1
xyaxyaxy
xyaxyaxy
, все a
ij
>0.
Запишем характеристический многочлен
21122211
)
2211
(
2
2221
1211
aaaaaa
aa
aa
−+++=
−−
−−
λλ
λ
λ
и найдем его корни
=
+−+±+−
=
2
2112
4
2211
4
2
22112211
21
)aaaa)aa(()aa(
,
λ
2
2112
4
2
22112211
aa))aa(()aa(
+−±+−
=
.
Следовательно, общий вид решения следующий:
y
1
(x) =
212111
21
ψψ
λλ
xx
ecec
+
y
2
(x) =
22
2
212
1
1
ψ
λ
ψ
λ
x
ec
x
ec
+
.
Одно значение λ отрицательно. Найдём, когда второе значение λ тоже отри-
цательно. Имеем неравенство
⇔<+−++−
0)
2112
4
2
)
2211
(()
2211
( aaaaaa
⇔+<+−
2
22112112
4
2
2211
)aa(aa)aa(
22112112
aaaa
<
.
Если выполнено последнее неравенство, то λ
1
<0 и λ
2
<0. Поэтому решения
будут удовлетворять условию y
1
(x) → 0 и y
2
(x) → 0 при х → +∞ . Это озна-
чает, что в этом случае гонки вооружения не будет, так как число единиц
вооружения у обеих сторон стремится к нулю. Таким образом, если произве-
дение коэффициентов страха (а
12
и а
21
) сторон меньше произведения коэф-
фициентов усталости (а
12
и а
21
) их экономик, то гонки вооружения не будет.

167
УХОБОТОВ Виктор Иванович
МАТЕМАТИКА ДЛЯ ЭКОНОМИСТОВ
Учебное пособие
Редактор Н.П.Мирдак
Компьютерная верстка Т.В.Ростуновой
Подписано в печать 30.12.02.
Формат 60х84
1
/16
. Бумага офсетная.
Печать офсетная. Усл. печ. л. 9,7. Уч.-изд. л. 13,0.
Тираж 500 экз. Заказ 311.
Цена договорная
Челябинский государственный университет
454021 Челябинск, ул. Братьев Кашириных, 129
Полиграфический участок Издательского центра ЧелГУ
454021 Челябинск, ул. Молодогвардейцев, 57б
