Тынкевич М.А. Лабораторный практикум
Подождите немного. Документ загружается.

Лабораторная работа 8. Решение обыкновенных дифференциальных уравнений
20
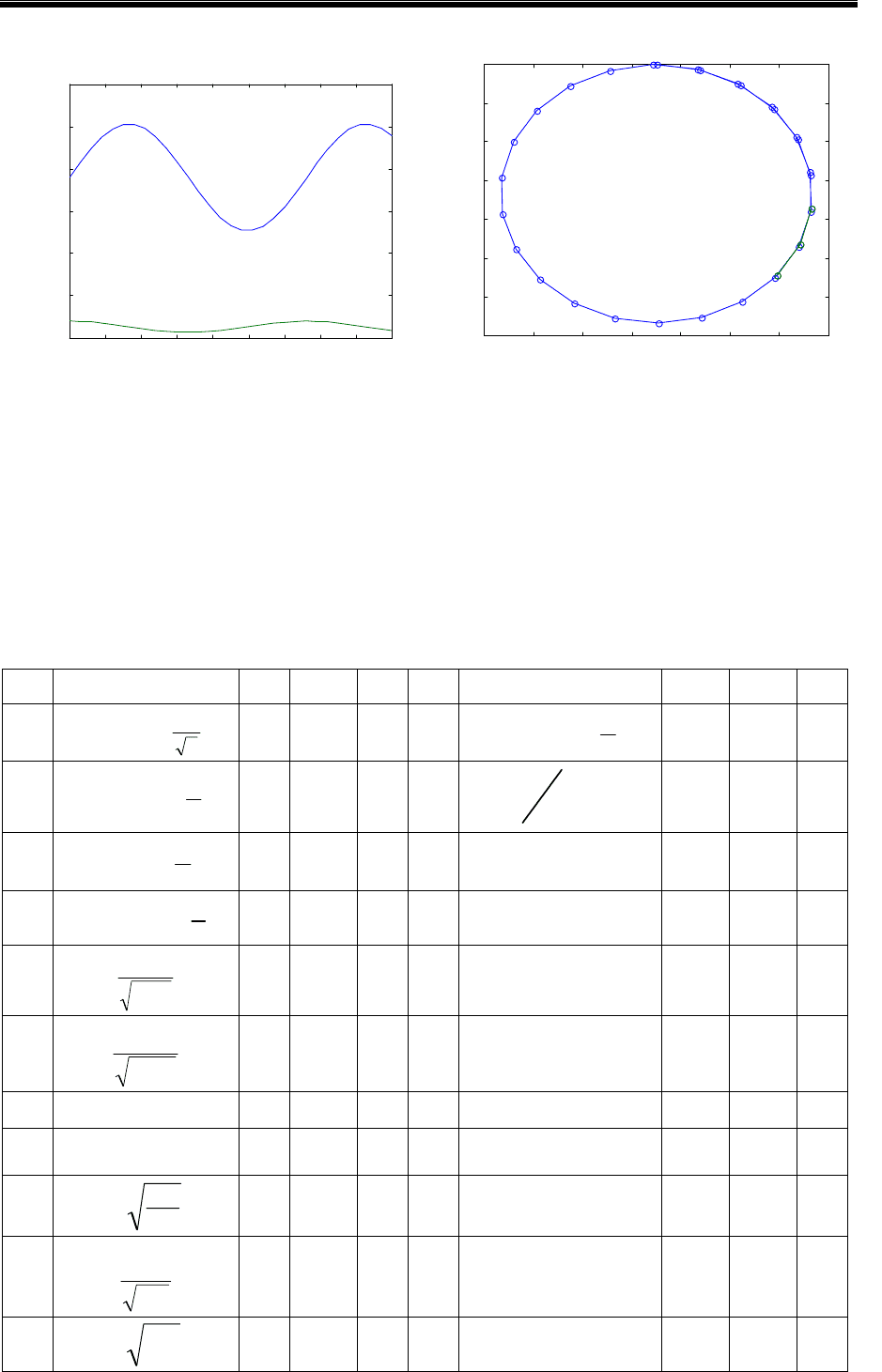
» [T,Y]=ode45('odu2', [0:0.3:9],[19 2],opt);
то будет выведен фазовый портрет системы, свидетельствующий о ее
устойчивости – гармонии между активом и ценами (рис.2).
Выясните, как сказывается на решении соотношение между d
0
и s
0
.
Варианты заданий
№ f(t,y) t
0
t
k
y
0
№ f(t,y) t
0
t
k
y
0
1
5
y
3
cost ⋅
0 1 3 14
3
y
sintln ⋅
1 2 0
2
3
y
costln ⋅
1 2 0 15
2
t1
y
−
0 0.5 1
3
3
y
tgt ⋅−
0 2 1 16
ty
2
0 2 1
4
3
y
2
sin/tln
1 2 0 17
t2
ye
−
0 1 1
5
4t
ty
2
−
2 3 1 18
t2
tye
−
0 1 1
6
4t
ty
2
2
−
2 3 1 19
t22
yet
−
0 1 1
7
tg(t)/y
2
0
π/4
1 20
tg(t)/y
0
π/4
1
8
t2
ye
0 1 1 21
y
2
t
2
0 1 1
9
t1
t1
y
−
+
0 1 1/e
22
y
2
/t
2
1 3 1
10
t1
yt
2
+
0 1 1/e
23
y ln(t) / t
1 3 1
11
3
2
y3
0 1 0
24
y
2
ln(t) / t
1 3 1
0 1 2 3 4 5 6 7 8 9
0
5
10
15
20
25
30
12 14 16 18 20 22 24 26
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Рис.1 Рис.2

Лабораторная работа 8. Решение обыкновенных дифференциальных уравнений
21
12
2
)t1(
t2
y2
t
−
−
⋅
0 0.9 0
25
2/t
ye
0 1 2
13
5
y
3
sint
0 1 3 26
ctg(t)/y
2
π/4 π/2
1
Лабораторная работа 9
Методы оптимизации
Задание 1. Выберите функцию из заданий к лабораторной работе
4, постройте ее график средствами MatLab’а в разумном диапа-
зоне для поиска точек ее экстремумов (наибольшего и наименьшего
значений) с заданной точностью (порядка 5 верных знаков) .
Задание 2. Для выбранной функции найдите наибольшее значение
взятием производной и решением возникающего уравнения f’(x)=0.
Задание 3. Для выбранной функции найдите наибольшее значение
методом чисел Фибоначчи.
Задание 4. Для выбранной функции найдите наименьшее значение
методом наискорейшего спуска.
Задание 5. Рассмотрите решение поставленных задач стандарт-
ными средствами оптимизации MatLab’а.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Тынкевич М.А. Численные методы. – Кемерово: КузГТУ. 1997. –
122 c.
2. Тынкевич М.А. Система MATLAB.Справочное пособие к курсу
“Численные методы анализа”– Кемерово: КузГТУ. 2001. – 47 c.
3. Потемкин В.Г. Система инженерных и научных расчетов
MATLAB 5.x. В 2-х т. –M.: ДИАЛОГ-МИФИ. 1999. – 670 c.
4. Плис А.И., Сливина Н.А. MATHCAD 2000. Практикум для эконо-
мистов и инженеров. -M.: Финансы и статистика. 2000. – 656 c.
5. Бахвалов Н.С. , Жидков Н.П. , Кобельков Г.М. Численные методы.
- М.: Наука ,1987.
6. Самарский А.А., Гулин А.В. Численные методы. - М.: Наука, 1989.
7. Марчук Г.И. Методы вычислительной математики. - М.: Наука,
1980.

Лабораторная работа 9. Методы оптимизации
21
8. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной
математике. - М.: Высшая школа, 1990.
9. Копченова Н.В., Марон И.А. Вычислительная математика в при-
мерах и задачах. - М.: Наука, 1972.
10. Мэтьюз Д.Г., Финк К.Д. Численные методы. Использование
MATLAB. –М.-СПб.-Киев: Вильямс, 2001.
Составитель
Моисей Аронович Тынкевич
Лабораторный практикум по курсу
“Численные методы анализа”
для студентов специальности
«Прикладная информатика в экономике»
ЛР № 020313 от 23.12.96
Подписано в печать 29.10. 2001. Формат 60х84/16.
Бумага офсетная. Уч.-изд.л. 1,25.
Тираж 150 экз. Заказ 437. Отпечатано на ризографе.
Кузбасский государственный технический университет.
650026, Кемерово, ул. Весенняя, 28.
Типография Кузбасского государственного технического
университета.
650099, Кемерово, ул. Д.Бедного, 4А.
