Труды Всемирного конгресса Международного общества солнечной энергии

Подождите немного. Документ загружается.

Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

572

horizontal evaporator heat transfer is in function.

When the horizontal evaporator heated by heat source, the

medium evaporated to vapor. The vapor flows through the

vapor channel of upper part of the evaporator where is no

liquid occupied up to the condenser part of the heat pipe,

then the condensed liquid flows back to one end of the

horizontal evaporator and melted in to the liquid reservoir.

In this circulation the heat is transferred from evaporator to

condenser by the horizontal heat pipe.

3. EVACUATED TUBE WITH HORIZONTAL HEAT

PIPE

The following different types of evacuated tubes with

horizontal heat pipe are developed.

3.1 Metal Glass Evacuated Tube with Horizontal Heat

Pipe

Fig. 1 shows the metal absorber collected solar heat

transfers from evaporator to condenser by the medium. The

evacuated tube may be horizontally installed in west east

direction. The absorber is flat and may be adjusted in any

slope angle to adopt the location altitude.

Fig. 1: Metal glass evacuated tube with horizontal heat pipe.

1-condenser 2-metal cover 3-horizontal heat pipe

4-metal absorber 5-glass tube

3.2 All Glass Vacuum Tube with Horizontal Heat Pipe

Fig. 2 shows the horizontal heat pipe is inserted into the all

glass vacuum tube. The cylinder metal fin is added between

the inner glass tube and the heat pipe evaporator for heat

conduct. Compare to all glass vacuum tube itself this

modified collector has advantages of not direct use water in

the inner glass tube of the vacuum tube. The leakage and

broken problems are avoided.

Fig. 2: All glass vacuum tube with horizontal heat pipe.

1-condenser 2-metal cover or rubber plug 3-all glass vacuum tube

4-heat pipe 5-metal fin

3.3 Long Insulator Horizontal Heat Pipe for the

Evacuated Tube

Fig. 3 shows the difference from Fig. 2 is the horizontal

heat pipe has longer insulator between the condenser and

evaporator. This design may adopt the solar water heater

tank and the evacuated tube is separated placed in a certain

distance but the water tank located above the tube. In this

case the insulator is made by flexible tube for easy

installation.

Fig. 3: Long insulator horizontal heat pipe for the all glass

vacuum tube.

1-condenser 2-long insulator 3-metal cover or rubber plug 4-all glass

vacuum tube 5-horizontal heat pipe 6-metal fin

4. SOLAR EVACUATED TUBE COLLECTORS WITH

HORIZONTAL HEAT PIPE

According to the different construction building

requirement the different evacuated tube collectors with

horizontal heat pipe are developed.

4.1 Metal Glass Evacuated Tube Collector with

Horizontal Heat Pipe

As shown in Fig.4 several metal glass evacuated tube with

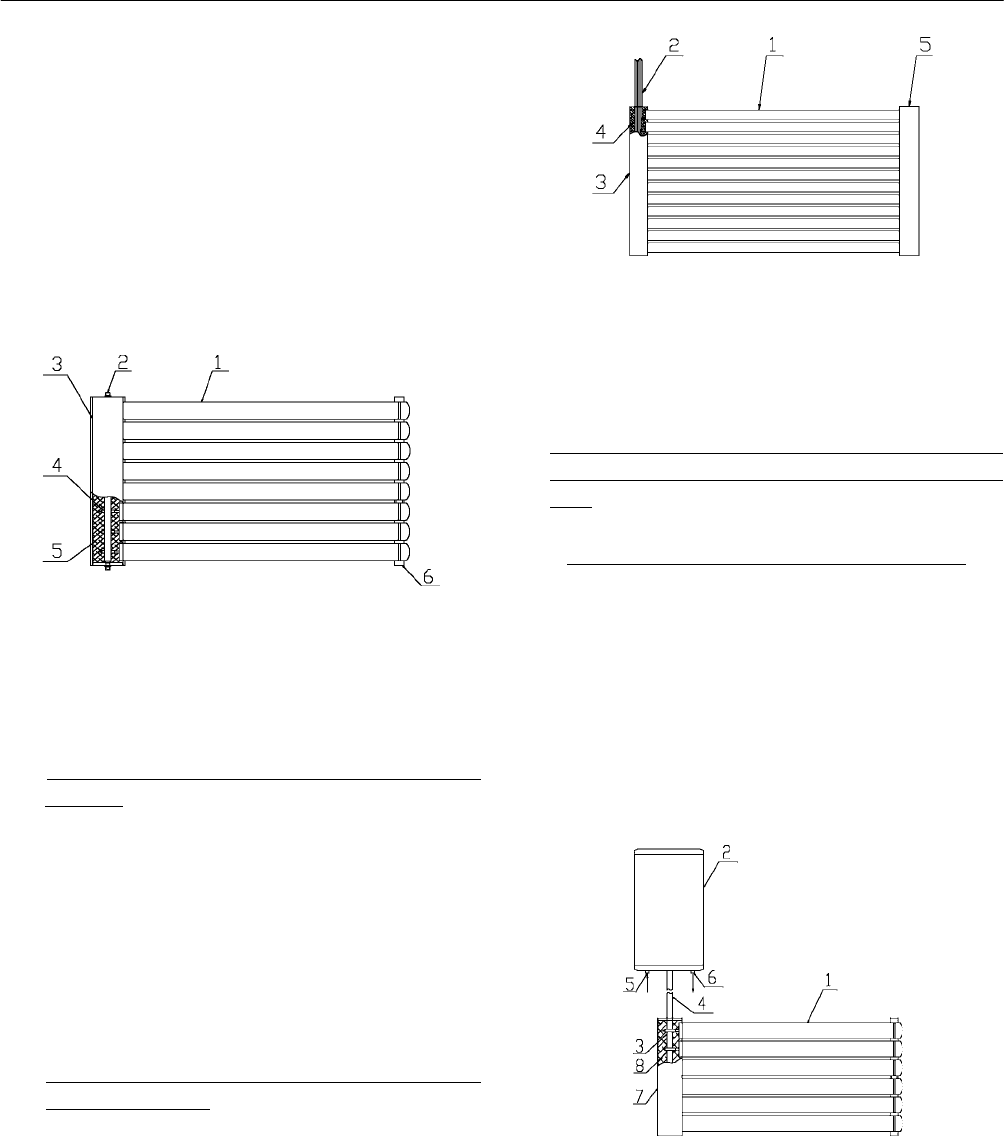
3 SOLAR COLLECTOR TECHNOLOGIES AND SYSTEMS

573

horizontal heat pipe, manifold, insulation casing are

assembled together as one unit of collector The condenser

is inserted in to the conductive metal block or tube which

connected to the manifold( dry connection). The absorber

sheet slope has to be adjusted in optimum angle for the

installation altitude.

The advantage of the dry connection is the circulation

liquid in the manifold is not mixed with the heat pipe

medium. The collector is stable in operation and easy to

maintenance.

Fig. 4: Metal glass evacuated tube collector with horizontal

heat pipe.

1-evacuated tube with horizontal heat pipe 2-manifold

3-casing 4-conductive tube or block 5-insulation

6-base support

4.2 All Glass Vacuum Tube Collector with Horizontal

Heat Pipe

All glass vacuum tube collector with horizontal heat pipe is

similar to the metal glass evacuated tube collector with

horizontal heat pipe. The only difference is the metal glass

tub is replaced by all glass vacuum tube. Because the all

glass vacuum tube characterized as cylinder inner absorber

glass tube ,when it is horizontal placed in east west

direction no slope angle is concerned.

4.3 Evacuated Tube Collector with Long Insulator

Horizontal Heat Pipe

Fig. 5 shows the collector is consisted by several evacuated

tubes with long insulator. There is no manifold in the

collector, each condensers of all heat pipe may be directly

inserted in to tank.

Fig. 5: Evacuated tube collector with long insulator

horizontal heat pipe.

1-evacuated tube collector with horizontal heat pipe

2-long insulator 3-casing 4-insulation 5-base support

5. THE APPLICATION SYSTEMS OF EVACUATED

TUBE COLLECTOR WITH HORIZONTAL HEAT

PIPE

5.1 Double Heat Pipe Solar Water Heater for Balcony

Fig. 6 shows the collector manifold is replaced by the

second heat pipe evaporator. The condenser of the second

heat pipe is inserted directly into the water tank. The east

west direction installed horizontal evacuated tube with

horizontal heat pipe collects solar energy and transfers the

heat through the second heat pipe into the water tank.. This

collector could be almost vertical hanged on the balcony

with the tank separated in the balcony.

Fig. 6: Double heat pipe solar water heater for balcony.

1-evacuated tube collector with horizontal heat pipe 2-tank

3-second heat pipe evaporator 4-second heat pipe insulator

5-inlet 6-outlet 7-casing 8-insulation

Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

574

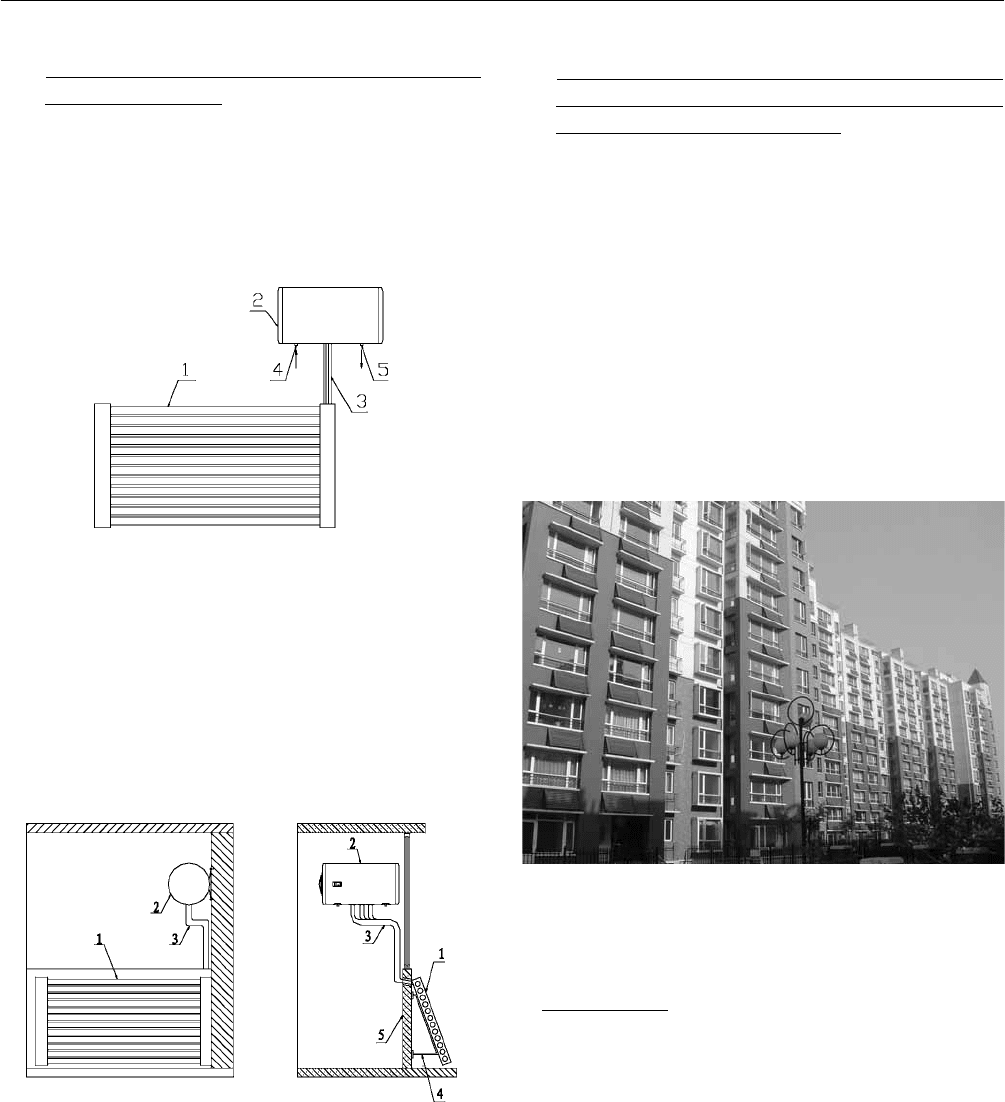
5.2 Solar Water Heater with Long Insulator Horizontal

Heat Pipe for Balcony

Fig. 7 shows each heat pipe unit directly transfers the heat

from the collector to the tank by means of the heat pipe

condenser directly inserted into the water tank.. This heat

transfer mechanism is more efficient and simple.

Fig. 7: Solar water heater with long insulator horizontal

heat pipe for balcony.

1-evacuated tube collector with long insulator horizontal heat pipe 2-tank

3-long heat pipes 4-inlet 5-outlet

Fig. 8 shows how the solar water heater is constructed on the

balcony or the facade. As pointed before the collector even

could be installed completely vertical closing to the wall but

the evacuated tubes are east west direction horizontal.

Fig. 8: Solar heater water installed on balcony.

1-evacuated tube collector with horizontal heat pipe 2-water tank with

electric heater 3-collector support 4-wall of the balcony

6. DEMONSSTRATION PROJECT OF BUILDING

INTEGRATED SOLAR HOT WATER HEATER

WITH HORIZONTAL HEAT PIPE

“Four season garden” apartment building project is

constructed by Shanxi Datang company. This project is

listed as one of the National demonstration building of

health living engineering projects. In this garden buildings

110 solar hot water heaters with horizontal heat pipe are

installed on the balconies of the apartment. From its start to

put to use from May 2005,the inhabitants are quite satisfied

with thermal performance. The integration of the solar

collector systems with the multi layer building are

demonstrated to be accepted by architectures.

Fig. 9: 110 Solar hot water heaters with horizontal heat pipe

installed in Shanxi Four season garden.

7. REFERENCES

Jiang xinian, Gao hansan, Ge hongchuan. A coreless

horizontal heat pipe for vacuum tube solar collector. China

Patent, No: ZL031100165.3, Date: 2003 Jan 8.

OPTICAL PERFORMANCE ANALYSIS FOR CONCENTRATING SOLAR COLLECTOR

APPLYING PARABOLIC AND CYLINDRICAL STATIONARY REFLECTOR

Jun Dong, Ζhifeng Wang

Institute of Electrical Engineering,

Chinese Academy of Sciences, Beijing 100080, P.R.China

ABSTRACT

In the present paper, the optical performance of the

concentrating solar collector applying parabolic and

cylindrical stationary reflector is investigated. And the

tracking path of the receiver tube can be extracted.at last

beam solar irradiance instantaneous intersection ratios with

parabolic and cylindrical stationary reflector can be worked

out. To deal with these data using MATLAB, the optical

performance at different solar terms in Beijing for the two

types of collector be worked out. A few common problems

met in work are discussed.

1. INTRODUCTION

There is a growing interest in building integrated solar

systems. Nevertheless, although it is possible to find some

commercially available building integrated systems for low

temperature thermal applications and non-concentrated PV,

very few systems combine building integrability with solar

radiation concentration. This poses a serious a handicap for

the introduction of some advanced technologies as solar

cooling and concentrated PV.

Apart from low concentration (C<5) systems such as CPC

collectors, most concentrating systems require some kind of

sun tracking. Usually this is accomplished by orienting the

concentrator aperture to the sun, although this procedure

impedes the integration of the reflector into building

elements such as walls and roofs, as the concentrator is a

moving element. An alternative solution which can reach

medium concentration levels consists of a system where the

tracking is accomplished by the receiver, with the

stationary reflector.

A simple design that combines a static parabolic or

cylindrical reflector with a tracking receiver positioned

along a path, the static reflector concentrate sun light onto a

linear thermal receiver. For any change in the incident

angle, the reflected rays will always intersect in different

points of the tracking path, therefore, it would be possible

to track the sun movement simply by positioning the

collector on the correct position of the tracking path,

without moving the reflector.

2. TRACKING PATH

2.1 Cylindgical Reflector Tracking Path

The use of a cylindrical concentrator results in large optical

aberrations, creating a caustic, or envelope, pattern to

which the reflected rays are tangent[1]. It can be easily

demonstrated that, for cylindrical reflector the tracking path

is a circle. As illustrated in Fig. 1.

The receiver has an evacuated annulus between the 42 mm

stainless steel absorber tube and the surrounding glass

cylinder. The receiver tube also has a 90mm flat fin as

shown in Fig. 2. The receiver has an acceptance angle of

120° degrees, which limits the reflector area viewed by the

Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

576

receiver to less than its full width. The full aperture width

of the reflector is 3660 mm, but the maximum aperture

width that can be viewed by the secondary reflector is

2000mm. The fixed maximal intersection ratio is therefore

54.6% when the incidence angle between -25° to 25°.

Fig. 1: Cylindrical concentrator.

Fig. 2: Receiver.

2.2 Parabolic Reflector Tracking Path

It is well known that a parabola has a point focus at a

normal incidence; nevertheless, it can be shown that for any

other incidence angle, all rays are concentrated into an area.

Therefore the smallest possible region intersecting all of the

reflected radiation will be the receiver position as shown in

Fig. 3. The analysis consisted in a ray tracing computation

of the average intersection ratio versus sun angle, followed

by using the obtained curves to determine the tracking path.

The ray tracing calculations were carried out using a

custom software program created by the authors based on

the forward ray tracing procedure. With this software, rays

were generated at random points of a squared window

oriented perpendicular to the sun’s direction, with an verage

Fig. 3: Parabolic concentrator.

density of 1 ray per unit surface. These rays were then

traced until they either struck a non specular surface or

were lost into space. During this process, a count of the

number of rays that have eventually reached the receiver

was performed, and at the end the average intersection ratio

is obtained as the total number of rays that struck the

receiver divided by the total number of rays that struck the

specular surface.

The receiver’s width is only 90mm.Therefore the receiver

will intersect the reflected radiation as much as possible.

The intersection ratio grows as the incidence angle

decreases and the tracking path and intersection ratio can be

simulated by MATLAB. As illustrated in Fig. 4 and Fig. 5.

The width of the parabola is 2500mm, the focal length f is

2000mm. The tracking path is a circle with a diameter D

that equals 8000mm.

Fig. 4: Intersection ratio of parabolic concentrator.

3 SOLAR COLLECTOR TECHNOLOGIES AND SYSTEMS

577

Fig. 5: Tracking path of parabolic concentrator.

It can be shown that at large incidence angles the

collector’s intersection ratio will be low. From the sun’s

movement path, if the collector at N-S orientation the

incidence angle will be mostly larger than that at E-W

orientation annually in Beijing (2). The determination of

the optimal orientation for a given application would

require a particular analysis for that case. But in this paper

the collectors will be at E-W orientations.

3. OPTICAL PERFORMANCE ANALYSIS

The analysis consisted in the ray tracing computation of the

average intersection ratio versus time, followed by using the

obtained curves to evaluate the optical efficiency of the system

in the four seasons for Beijing at a latitude of 40° N. The slope

of the aperture is 30° smaller than the latitude of Beijing.

The average optical efficiency obtained by the system is the

ratio of the energy captured by the receiver over a one day

period to the beam radiation intercepted in the same period by

the reflector aperture. For the Beijing geometries, integration

was performed over three days: 22th December, 21th March

and 22th June, these there days serving as representatives of

the winter, spring and summer weather conditions.

The results obtained from the two different reflectors were

quite different, cylindrical concentrator had an almost fixed

intersection ratio which is 54.6%, while the intersection

ratio of parabolic concentrator are functions of the

projected sun elevation and need to be evaluated by time.

In general, during spring and autumn, the intersection ratio

of parabolic concentrator is slightly higher than that of

cylindrical concentrator, but during summer and winter, the

result is opposite as shown in Fig. 6. 7. 8.

Fig. 6: Parabolic intersection ratio in spring and autumn.

Fig. 7: Parabolic intersection ratio in summer.

Fig. 8: Parabolic intersection ratio in winter.

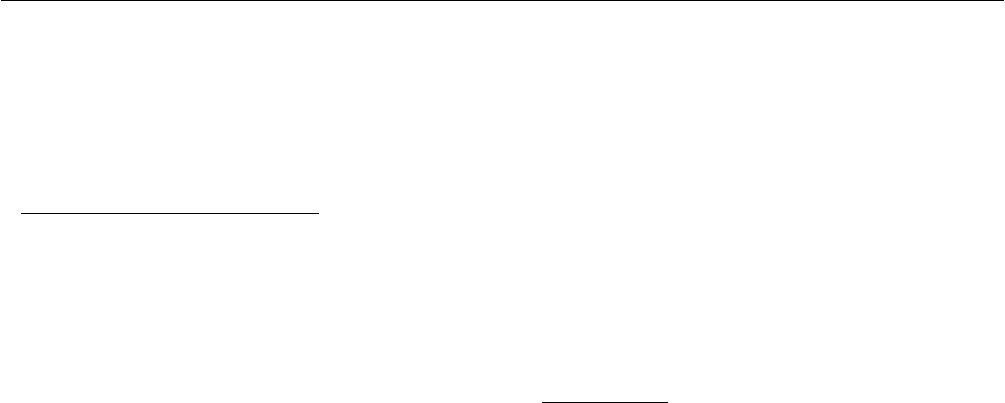
Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

578

there may be very low intersection ratio for cylindrical

concentrator at morning and eve. This is due to the fact that

some reflected radiation was not covered by the acceptance

angle.

4. CONCLUSION AND DISCUSSION

The results obtained show that it is theoretically possible to

obtain acceptable optical efficiencies combining a

stationary reflector and a tracking receiver, and the tracking

path diameter can be extracted and simulated. In general,

the optical performance of parabolic stationary reflector is

quite different in different season while that of the

cylindrical concentrator is fixed.

Nevertheless, in order to evaluate the overall behaviour of a

given design, it is necessary to keep in mind that, at a given

location (and for a given time period), the energy received

at different sun angles is non uniform, in fact it is even

possible that some angles would not have any use at all.

Taking this in mind, at a latitude of 40° N for the summer

season, it would be possible to reach hi.

On one hand, this geometry, in comparison to the Fresnel

like design, has the advantage of being a single, continuous,

smooth surface, which is clearly advantageous from a

manufacturing point of view, while this design also has

some drawbacks; uneven radiation distribution striking the

receiver can lead to an inefficient energy conversion.

Moreover, radiation dispersion at large incidence angles

can produce significant energy losses, especially at high

concentration ratios. Therefore a study should been

conducted in order to analyze those problems and to

understand its influence on the system performance.

5. REFERENCES

(1) andy Gee,“Operation and preliminary performance of

the DUKE solar power roof: A roof-integrated solar

cooling and heating system” http://www.solargenix.com/

(2) hen Wei,“Optical performance of analysis for

parabolic-trough focusing collector with several

tracking modes”Acta Energiae Solarris Sinica ,Vol 24,

No.4 p.477

THE OPTIMIZED OPTICAL REQUIREMENT FOR SPECTRALLY

SELECTIVE ABSORBERS

Shuxi Zhao

Uppsala University, The Ångström Laboratory,

P.O. Box 534, S-751 21 Uppsala, Sweden

Shuxi.Zhao@angstrom.uu.se

Ewa Wäckelgård

Uppsala University, The Ångström Laboratory,

P.O. Box 534, S-751 21 Uppsala, Sweden

ABSTRACT

It is investigated how the intrinsic optical properties of the

metal and dielectric constituents in composite spectrally

selective solar absorber coatings influence its solar

absorptance and thermal emittance. Theoretical modeling

using Bruggeman effective medium theory has been used to

analyze the basic features in the effective optical constants

of the composite layer that are required in order to obtain

high solar absorptance in combination with low thermal

emittance. It is found that the requirement is correlated to

certain dispersion of extinction coefficient and refractive

index. The metallic content of used composite should be

large enough to give a reasonable extinction coefficient, but

not beyond the metal-nonmetal transition point. The ideal

dispersion for refractive index should decrease with

increasing wavelength in the transition wavelength region.

So does the extinction coefficient.

1. INTRODUCTION

A spectrally selective solar absorbing surface for

solar-thermal conversion requires a low reflectance in solar

wavelength range, and high reflectance in infrared

wavelength range, as well as a steep transition in the

reflectance from low to high value at wavelengths between

the solar and the thermal infrared wavelength ranges. For

moderate temperatures (50 to 100°C) applications, this

transition is situated at about 2.5 µm. The most commonly

used selective surface is the absorber/reflector tandem. The

coating material for absorber is highly absorbing in the

solar range, but highly transmitting in the infrared range.

When such material is coated on a highly infrared

reflecting substrate, forming absorber/reflector tandem, it

shows good spectral selectivity. Metal-dielectric

composites, also known as cermets, are widely used as

coating materials [1]. The actual metal, dielectric, and

metallic content will affect the optical performance of the

composite. This paper reports the optical requirement of

such a composite for obtaining a good spectral selectivity

and steep reflectance transition using Ni-NiO since it is

widely used in a flat-plate collectors in Europe. It provides

a reasonable reference for comparison with different

composite materials.

2. BACKGROUND

The optical properties of cermets with small particles can

be modeled using effective medium theory (EMT). The

simplest models are the Maxwell-Garnett and Bruggeman

models for spherical particles. We have chosen the

Bruggeman model in this study since our studied

nickel-nickel oxide coatings resemble an aggregate

structure more than metal inclusions in a dielectric matrix.

We also use spherical particles as a simplification of the

granular observed with transmission electron microscopy

[2]. The Bruggeman effective medium approximation for

spherical particles is given in equation [1,3]:

Proceedings of ISES Solar World Congress 2007: Solar Energy and Human Settlement

580

(1 ) 0

εε εε

−−

+− =

(1)

where f

is the volume fraction of metallic component, ε

stands for dielectric functions, indexed by M for the metal,

D for the dielectric component respectively, and ε

for

dielectric function of metal-dielectric composite obtained

from Bruggeman model.

The optimization of the spectral selectivity is made from

the optical reflectance of a modeled absorber coating in the

wavelength range 0.3 to 30 µm in order to cover the

spectral range of the solar radiation as well as the range for

the main part of the thermal radiation. The absorber is

modeled as a two-dimensional stack of layers of

homogeneous thickness, with smooth front surface and

interfaces between the layers and in-plane infinite

dimension neglecting edge effects.

As reported in [4], three-layer (base-layer, middle-layer,

and anti-reflection layer on the top) is a simple structure

with good spectral selectivity where the base-layer is the

main solar absorbing layer in this structure. So we only

analyze a single absorbing layer for further simplification.

For a single film on a substrate, the total amplitude

reflection is [5]

err

−

(2)

where r

, r

presents represents the amplitude reflection at

the surface (air/thin film), and film/substrate interface

respectively. For normal incidence, the phase change in the

thin film is given as

=− ⋅

(3)

where d

is the film thickness, λ is the vacuum wavelength

of the incident light, N

represents the complex optical

constants of thin film material.

In order to study intrinsic and interference-induced

absorption of thin film, the phase factor

2 δi

−

in equation

(3) can be expressed as

(cos(4 / ) sin(4 / ))endindπλ πλ⋅⋅+⋅

(4)

Substituting 4n

/λ with the interference order parameter

[6], equation (5) can be simplified as

24/

(cos( ) sin( ))

ikd

ee mim

δπλ

ππ

−⋅ −⋅⋅

=⋅ +

(5)

The subscript in equation (5) was omitted for discussion of

one layer. The phase factor shows explicitly the influence

of both intrinsic absorption determined by the extinction

coefficient, k, and interference-induced absorption

determined by the refractive index, n. As n and k are

interrelated, their values cannot be varied independently.

Their optical response cannot be separated but we will in

the following analysis use them and distinguish important

features for obtaining good spectrally selective solar

absorbers.

The extinction coefficient determines the light attenuation

in the interior of the film. The periodic terms in equation (5)

determines the phase shift of light in the interface passages

and as such they will influence the transition from low to

high reflectance between the solar and infrared wavelength

range. The term cos(mπ) indicates the wavelength position

of the first optical interference minimum for m=1. The term

sin(mπ) gives a pure imaginary phase factor and indicates

the wavelength of high reflectance for m=0.5. We have

found that m=0.5 is positioned on the long wavelength side

of the reflectance transition.

The ideal optical response regarding its intrinsic optical

constants requires a high enough extinction coefficient in

the solar wavelength range to give a total attenuation for a

light passing the distance of 2d. The ideal response

regarding a steep reflectance transition between the solar

and thermal wavelength ranges is governed by optical

interference and a narrow wavelength range between the

wavelengths positions for m=0.5 and m=1. This will be

determined by the dispersion of the refractive index. It is

also required that the extinction is low in the transition

wavelength range as well as in the remaining infrared

range.

3 SOLAR COLLECTOR TECHNOLOGIES AND SYSTEMS

581

3. RESULTS AND DISCUSSION

3.1 Extinction Coefficient

In this section we will analyze the optical constants of the

nickel nickel-oxide cermet used in a base layer. The optical

constants are calculated using the Bruggeman effective

medium model. The dielectric function of Ni and NiO is

from references [7, 8].

The intrinsic absorption is determined by the extinction

coefficient. Figure 1 shows the dispersion in the effective

extinction coefficient for five nickel-volume fractions: 0,

0.10, 0.18, 0.30, and 0.38. The contribution to the

extinction coefficient from the metal content is dominating

in the wavelength range between 320 nm to 18 µm, which

is the wavelength range where the oxide is transparent. The

UV and far infrared wavelength range are regions where

the extinction has a large contribution from the nickel oxide

due to electronic interband-transition and lattice vibration

respectively. However these contributions play a minor role

in the performance of the spectrally selective coating

because the solar intensity is low below 320 µm, and the

coating is very thin and will therefore emit very little in the

infrared.

Fig. 1: Extinction coefficient of Ni-NiO calculated by

Bruggeman model at five different nickel volume

fractions: 0, 0.10, 0.18, 0.30, and 0.38.

The impact of the metal content is that k increases with

increasing nickel content and also covers a larger range

being non-zero. However, too large nickel content will

result in that k is larger than n with high reflection

(behavior like metal) which is not wanted. So the metal

content must be limited by this requirement.

3.2 Refractive Index and Interference

Figure 2 shows the dispersion of n at five nickel-volume

fractions indicated in figure 1. The refractive index varies

very little with nickel content for wavelengths shorter than

1µm. However as the metal content increases the refractive

index increases with nickel content in the interval from 1 to

about 15 µm. When metal content is as large as 0.38, n

starts to reduce which indicates the metal-nonmetal

transition of the composite [9]. In the long wavelength

range displayed in the figure the oxide dominates the

dispersion due to lattice vibrations. However this impact is

weak due to the thinness of the coating. One important

feature, as mentioned earlier, is to create a sharp reflectance

transition in the wavelength range 2 to 3 µm. This means

that the wavelength interval between parameter m = 0.5 and

m = 1 should be as narrow as possible. This is illustrated in

figure 3 for two cermets with different metal content (but

the same thickness). The interval is much smaller for the

lower metal content because the refractive index is nearly

constant in this range while it is increasing for cermet with

Fig. 2: Refractive index of Ni-NiO calculated by

Bruggeman model at five different nickel volume

fractions: 0, 0.10, 0.18, 0.30, and 0.38.

Труды Всемирного конгресса Международного общества солнечной энергии - 2007. Том 2

Подождите немного. Документ загружается.