Трошин Л.И. Балаш В.А. Балаш О.С. Статистический анализ нечисловой информации
Подождите немного. Документ загружается.

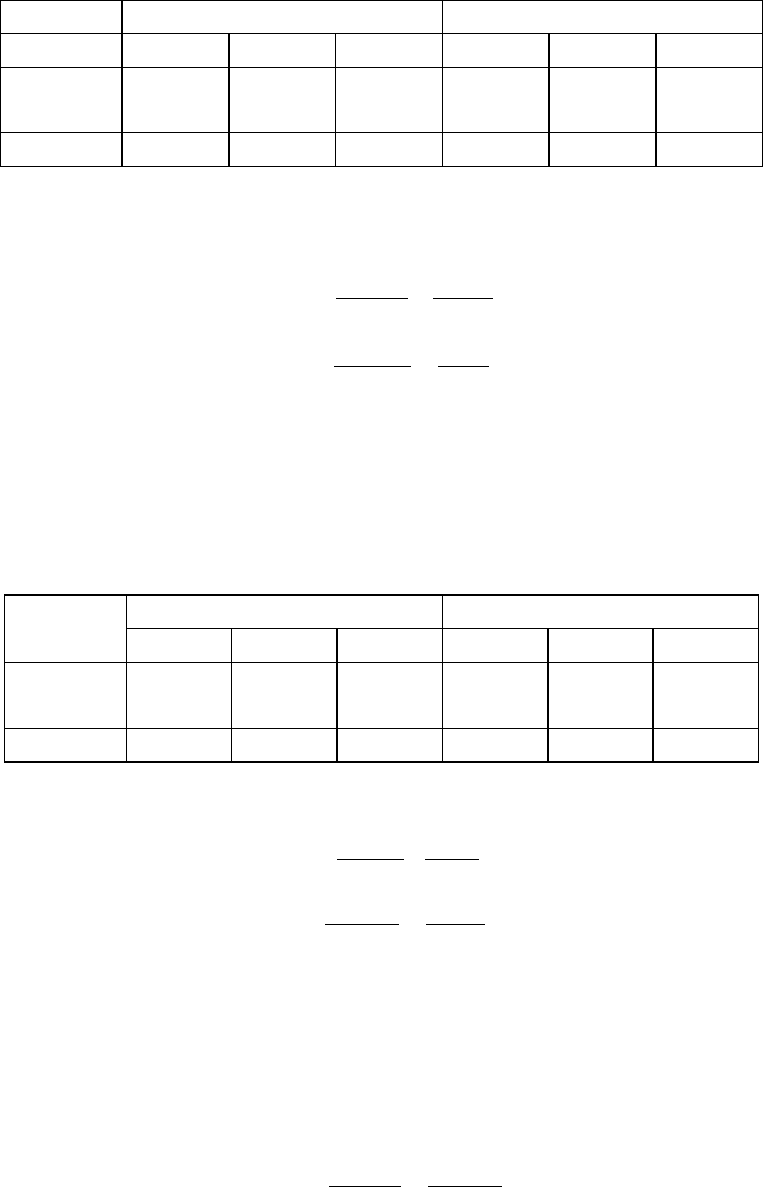
Перестроим таблицу следующим образом:
Y
1
Y
2
Z
1
Z
2
Всего Z
1
Z
2
Всего
Х
1
15 28 43 5 12 17
Х
2
15 42 57 5 18 23
Всего 30 70 100 10 30 40
Аналогично найдем отношение преобладаний:
5,1
2815
4215
112211
212111
=
⋅
⋅
==
Π
nn
nn
О
5,1
125
185
122221
222121
=
⋅
⋅
==
Π
nn
nn
О
.
Отношение преобладаний равно 1,5, что означает, что признак Х
и Z зависимы, связь положительна. То есть признаки «пол» и
«успеваемость» зависимы.
Аналогично можно показать, что Y и Z также взаимозависимы.
Построим таблицу сопряженности:
Х
1
Х
2
Z
1
Z
2
Всего Z
1
Z
2
Всего
Y
1
15 28 43 15 42 57
Y
2
5 12 17 5 18 23
Всего 20 40 60 20 60 80
Найдем отношение преобладаний для левой и правой таблицы:
;28,1
285
1215
112211
212111
=
⋅
⋅
==
Π
nn
nn
О
.28,1
425
1815
122221
222121
=
⋅
⋅
==
Π
nn
nn
О
Отношение преобладаний равно 1,28, т.е. признак Y и Х зависимы,
то есть признаки «выбранная специальность» и «успеваемость»
студентов.
Для определения взаимодействия трех факторов следует
рассмотреть следующее отношение вероятностей:
pp
pp
pp
pp
111 221
121 211
112 222
122 212
=
.
В этом случае имеет место отношение отношения преобладаний.
Это отношение определяет так называемое взаимодействие второго
порядка или трехфакторное взаимодействие.
Анализом связей между признаками, определением
взаимодействий между ними занимается логлинейный анализ.
31

4. Логлинейный анализ
4.1 Модель логлинейного анализа
Рассмотрим двумерную таблицу сопряженности r×s.
Представим теоретические частоты в ячейках такой таблицы в
виде:
ab
ij
b
j
a
i
uuuu
ij
en
+++
=
0
*
; (4.1)
или, в другой форме:
, (4.2)
ln
*
nuu u u
ij i
a
j
b
ij
ab
=+++
0
где: n
*
ij
–теоретическая частота в ячейке;
u – неизвестные параметры, называемые:
u
a
i
– эффект i-ой градации первого признака;
u
b
j
– эффект j-ой градации второго признака;
u
ab
ij
– эффект взаимодействия двух признаков;
u
0
– общий эффект;
i = 1,...r ; j = 1,...., s.
Параметры должны удовлетворять ограничениям:
uuuu
ij
ab
i
ij
ab
j
i
a
i
j
b
j
===
∑∑∑∑
0
=
. (4.3)
Подобные модели называют логлинейными моделями таблиц
сопряженности.
В логлинейной модели теоретические ожидаемые частоты n
*
ij
преобразуются в их логарифмы, представляющие собой сумму из
четырех параметров модели.
Параметры логлинейной модели иногда называют также вкладами,
вносимыми различными эффектами в теоретическую частоту.
Логлинейный анализ – это статистический анализ связи таблиц
сопряженности с помощью логлинейных моделей. Он позволяет в
сжатой форме с помощью относительно небольшого числа параметров
записать информацию, содержащуюся в таблице сопряженности. Кроме
того, логлинейная модель поддается содержательной интерпретации
получаемых результатов.
В общем виде наблюдаемую частоту n
ij
можно представить в виде
логлинейной модели:
ij
ab
ij
b
j
a
i
uuuu
ij
en
ε
++++
=
0
,
где
e
n
n
ij
ij
ij
ε
=
*
и i = 1,...r ; j = 1,...., s.
Таким образом,
является отклонением логарифма
наблюдаемой частоты от логарифма теоретической частоты, а
показывает относительное отклонение наблюдаемой, эмпирической,
частоты от ожидаемой теоретической, то есть определяет во сколько раз
n
*
lnlnln
ijij
nne
ij
−=
ε
e
ij
ε
ij
больше или меньше n
*
ij
.
32
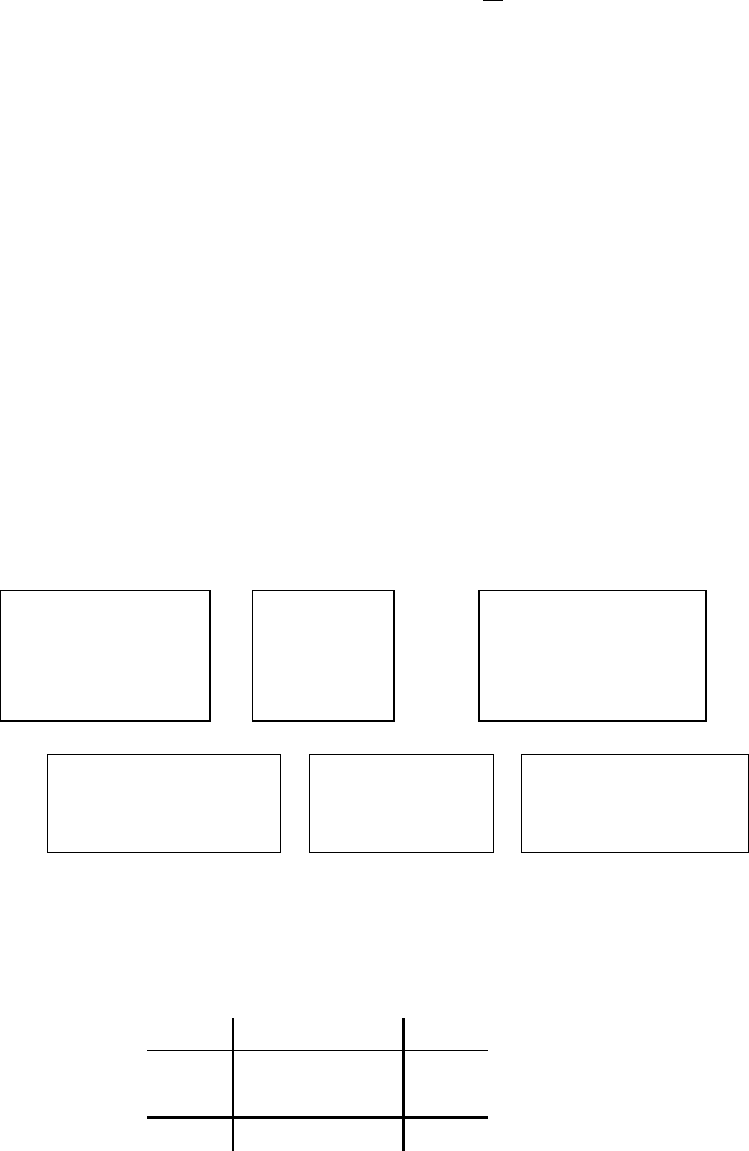
Для проверки гипотезы о независимости признаков:
},...,1;,...,1;0{:
*
0
sjriuH
ab
ij
===
вместо критерия χ
2
применяется критерий χ
2
инф
, статистика которого
имеет вид:
.ln2
*
2
∑∑
=
ij
ij
ij
ijI
n
n
n
χ
. (4.4)
При расчете статистики χ
2
инф
следует иметь в виду, что таблица
сопряженности не должна иметь нулевые или пустые клетки. Если такие
существуют, то для такой таблицы в пустые клетки добавляют числа,
заключенные в интервал от нуля до единицы, чаще 0,5, что помогает
избежать неопределенности.
При большом объеме выборки n статистики χ
2
и χ
2
инф
мало
отличаются друг от друга, поэтому вместо χ
2
инф
можно применить χ
2
,
однако при небольших объемах выборки желательно употреблять
информационный критерий.
Модель называется насыщенной, если она включает все факторы
и взаимодействия.
Число независимых параметров модели равно разности числа всех
параметров модели и числа ограничений, накладываемых на параметры
модели.
Число степеней свободы при проверке гипотез в таблице
сопряженности с помощью критерия χ
2
и χ
2
инф
определяются
следующим образом:
число степеней
свободы ν
= число
клеток
– число
независимых
параметров
модели
=
= число клеток
таблицы
– число всех
параметров
+ число
ограничений на
параметры
4.2 Оценка параметров насыщенной модели для таблиц 2×2
Пусть имеется выборочная таблица сопряженности 2×2.
X Y не В В n
i*
не А n
11
n
12
n
1*
А n
21
n
22
n
2*
n
*j
n
*1
n
*2
n
**
=n
Будем предполагать, что частоты во всех ячейках таблицы не
равны нулю.
33

Насыщенная модель имеет вид:
ab
ij
b
j
a
iij
uuuun
+++=
0
*
ln
, i =1,2; j=1,2. (4.5)
Число всех параметров, с учетом того, что i и j принимает по два
значения, а u
ij
ab
– четыре значения, равно: 1 + 2 + 2 + 4 = 9.
Число ограничений определяется из соотношения (4.3):
ababababababbbaa
uuuuuuuuuu
2211211112111212
;;;;
=−=−=−=−=
.
Число независимых параметров равно 9 – 5 = 4 и совпадает с
числом клеток таблицы 2×2. Следовательно, рассматриваемая модель
является насыщенной.
Для насыщенной модели число степеней свободы равно нулю для
таблиц сопряженности любых размеров. Вследствие этого
теоретические частоты не отличаются от наблюдаемых, то есть n
*
ij
= =
n
ij
. Значение критерия хи-квадрат должно быть равно нулю. Обычно
вместо критерия χ
2
используют критерий χ
2
инф
(4.4).
С учетом ограничений, накладываемых на параметры, для
таблицы сопряженности можно записать следующую систему
уравнений:
+−−=
−+−=
−−+=
+++=
abba
abba
abba
abba
uuuun
uuuun
uuuun
uuuun
11110
*
22
11110
*
21
11110
*
12
11110
*
11
ln
ln
ln
ln
. (4.6)
Решая данную систему относительно u, получим:
u
nn
nn
u
nn
nn
u
nn
nn
unnn
ab a
b
11
11 22
12 21
1
11 12
21 22
1
11 21
12 22
0111221
1
4
1
4
1
4
1
4
==
==
ln ; ln ;
ln ; ln( ).
**
**
**
**
**
**
****
n
22
(4.7)
Взаимодействие u
11
ab
равно логарифму отношения преобладаний
(1.4).
4.3 Оценка параметров ненасыщенных моделей для таблиц 2×2
Модель, у которой хотя бы один из параметров равен нулю,
называется ненасыщенной.
Для проверки гипотезы об адекватности любой ненасыщенной
модели применяется критерий (4.4).
а) Модель независимости
Если в насыщенной модели
следовательно, и
, то полученная ненасыщенная модель называется
моделью независимости или независимой моделью.
,0u
ab
ij
=
uuu
ab ab ab
12 21 22
0
===
34

Модель независимости в общем случае имеет вид:
b
j
a
iij
uuun
++=
0
*
ln
,
где теоретические частоты равны
n
nn
n
ij
ij
*
**
=
.
Если признаки независимы, то отношение преобладаний для
теоретических частот равно единице:
1
*
12
*
21
*
22
*
11
==
Π
nn
nn
О
.
Получаем следующие оценки параметров модели независимости:
uu
nn
nn
u
nn
nn
unnn
ab a
b
11 1
11 12
21 22
1
11 21
12 22
0111221
0
1
4
1
4
1
4
==
==
;ln
ln ; ln( ).
**
**
**
**
****
n
22
;
=
0
(4.8)
Если Х
2
инф
< Х
2
крит
, то модель считается адекватной и возможно
дальнейшее упрощение модели.
Число степеней свободы равно 4 – 3 = 1.
б) Модель с отсутствием влияния одного фактора
Модель с отсутствием влияния фактора В имеет вид:
.
a
iij
uun
+=
0
*
ln
Параметры
и, следовательно, теоретические частоты
можно рассчитать как
uu
ij
ab
j
b
=
0,
n
.
n
11
1
*
*
n
n
21
2
22
*
*
;
==
Таблица сопряженности теоретических частот для данной модели
имеет вид:
X Y не В В n
i*
не А n
1*
/2 n
1*
/2 n
1*
А n
2*
/2 n
2*
/2 n
2*
n
*j
n/2 n/2 n
**
=n
Из таблицы видно, что частное распределение категорий признака
В равновероятно, то есть фактор В не оказывает влияние на
распределение теоретических частот или вероятностей клеток таблицы.
Эффект фактора В равен нулю.
Параметры логлинейной модели:
uu
nn
nn
uun
ab a
b
11 1
11 12
21 22
1 0 11 12 21 22
0
1
4
0
1
4
==
==
;ln
;ln(
**
**
****
nnn
;
).
(4.9)
35

Аналогично строится модель с отсутствием влияния фактора А:
.
ln
*
nuu
ij j
b
=+
0
Таблица теоретических частот соответственно имеет вид:
X Y не В В n
i*
не А n
*1
/2 n
*2
/2 n/2
А n
*1
/2 n
*2
/2 n/2
n
*j
n
*1
n
*2
n
**
=n
Параметры логлинейной модели:
uu
u
nn
nn
unnn
ab a
b
11 1
1
11 21
12 22
0111221
00
1
4
1
4
==
==
;;
ln ; ln( ).
**
**
****
n
22
(4.10)
Число степеней свободы равно 4 – 2 = 2.
в) Равновероятная модель
Для этой модели отсутствует влияние фактора А и фактора В:
ln
*
nu
ij
=
0
.
Таблица теоретических частот в этом случае:
X Y не В В n
i*
не А n/4 n/4 n/2
А n/4 n/4 n/2
n
*j
n/2 n/2 n
**
=n
Параметры логлинейной модели:
uu
uun
ab a
b
11 1
1 0 11 12 21 22
00
0
1
4
==
==
;;
;ln(
****
nnn
).
(4.11)
Число степеней свободы равно 4 – 1 = 3.
На практике анализ логлинейных моделей можно проводить
начиная с насыщенной модели, постепенно ее упрощая.
Все виды логлинейных моделей представлены в табл. 4.1.
36

Таблица 4.1
Виды логлинейных моделей
Номер модели Название модели Вид модели
1. Насыщенная
ln
*
nu u u u
ij i
a
j
b
ij
ab
=+ ++
0
2. Независимости
ln
*
nuuu
ij i
a
j
b
=++
0
3. Нет фактора В
ln
*
nuu
ij i
a
=+
0
4. Нет фактора А
ln
*
nuu
ij j
b
=+
0
5. Равновероятная
ln
*
nu
ij
=
0
Для проверки значимости параметров модели, следует вычесть
χ
2
инф
из модели с высоким номером
χ
2
инф
модели с низким номером.
Если значение некоторых параметров при оценке параметров
оказывается близкими к нулю, то они из модели исключаются.
4.4 Иерархические модели
Рассмотренные модели входят в класс иерархических, которые
подчиняются правилу, выполняемому в многомерном случае. Допустим
в модель включен параметр, зависящий от множества S факторов. Тогда
модель должна включать также и все параметры, зависящие от любого
подмножества из этого множества факторов.
Например, если в какую-нибудь иерархическую модель включен
параметр
, то в нее обязательно должны входить и параметры
.
u
ij
ab
uu u
i
a
j
b
0
,,
Пример неиерархической модели:
. В модель включен
фактор u
ln
*
nu u
ij ij
ab
=+
0
ij
ab
, однако отсутствуют главные влияния обоих факторов А и В.
Таблица сопряженности такой модели может иметь вид:
X Y не В В n
i*
не А 80 20 100
А 20 80 100
n
*j
100 100 200
Из таблицы видно, что связь между А и В существует, однако
отсутствует влияние фактора А и фактора В отдельно.
37
4.5 Тренировочный пример
В результате маркетингового исследования, проведенного с целью
изучения эффективности рекламы среди 800 покупателей, получена
следующая таблица сопряженности по признакам:
А – пол (1– мужской; 2 – женский);
В – информация о рекламе товара (1 – знакомы; 2 – не знакомы).
А В 1- знакомы 2 - не знакомы n
i*
1-мужской 298 142 440
2- женский 210 150 360
n
*j
508 292 800
Найдем параметры всех логлинейных моделей, рассчитаем
статистику Х
2
инф
для каждой модели и проверим адекватность
полученной модели эмпирическим данным.
1. Насыщенная модель:
,
ab
ij
b
j
a
iij
uuuun
+++=
0
*
ln
i = 1, 2; j = 1, 2.
Для нахождения параметров и теоретических частот составим
таблицу логарифмов наблюдаемых частот: . yn
ij ij
=
ln
А В 1 - знакомы 2 - не знакомы
5,69 4,96
2- женский 5,35 5,01
1-мужской
Затем по формулам (4.5) находим параметры логлинейной модели,
пользуясь свойствами логарифмов:
u
nn
nn
nn n n
u
nn
nn
nn n n
ab
a
11
11 22
12 21
11 22 12 21
1
11 12
21 22
11 12 21 22
1
4
1
4
1
4
1
4
==+−−
==+−−
ln (ln ln ln ln );
ln (ln ln ln ln );
**
**
** * *
**
**
** * *
u
nn
nn
nn n n
unnnn nnnn
b
1
11 21
12 22
11 21 12 22
011122122 112112
1
4
1
4
1
4
1
4
==+−−
==++
ln (ln ln ln ln );
ln( ) (ln ln ln ln ).
**
**
** * *
**** * * * *
22
+
38
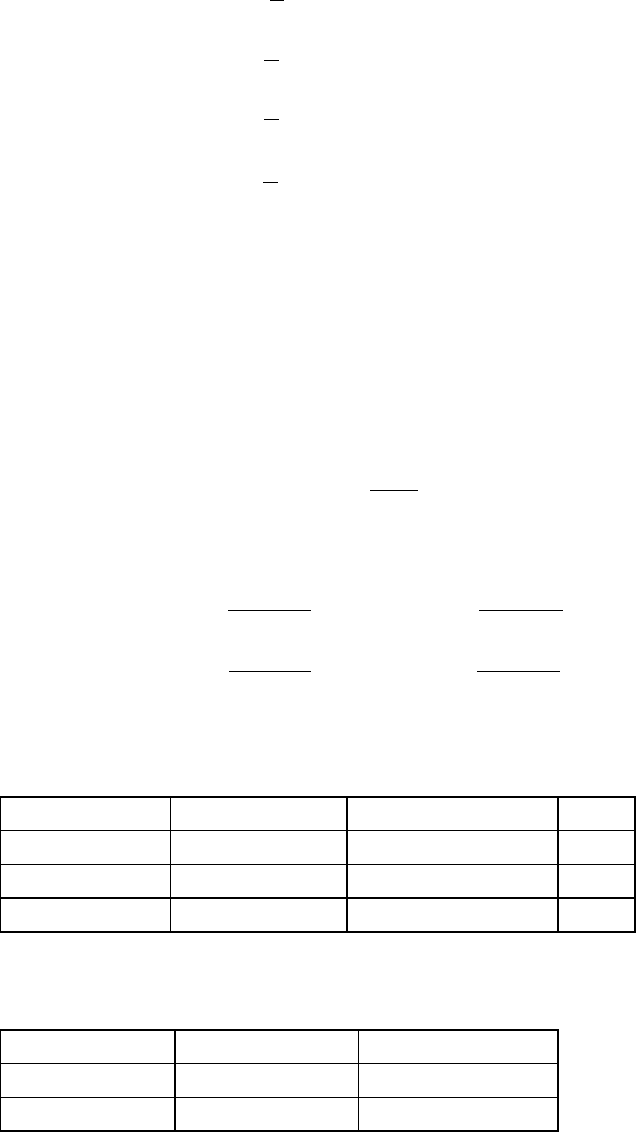
Получим:
u
ab
11
1
4
5 69 5 01 5 35 4 96 0 101
=+−−=
(, , , , ) , ;
u
a
1
1
4
5 69 5 01 5 35 4 96 0 269
=−+−=
(, , , , ) , ;
u
u
b
1
0
1
4
5 69 5 01 5 35 4 96 0 073
1
4
569 501 535 496 525
=−−+=
=+++=
(, , , , ) , ;
(, , , , ) , .
Так как для насыщенной модели теоретические частоты равны
фактическим, то статистика Х
2
инф
= 0.
2. Модель независимости:
b
j
a
iij
uuun
++=
0
*
ln
.
Для этой модели теоретические частоты находятся по формуле:
n
nn
n
ij
ij
*
**
=
.
Рассчитаем теоретические частоты:
nn
nn
11 12
21 22
440 508
800
279 4
440 292
800
160 6
360 508
800
228 6
360 292
800
131 4
**
**
,; ,;
,; ,.
=
⋅
==
⋅
=
=
⋅
==
⋅
=
Таблица теоретических частот:
А В 1- знакомы 2 - не знакомы n
i*
1-мужской 279,4 160,6 440
2- женский 228,6 131,4 360
n
*j
508 292 800
Составим таблицу логарифмов теоретических частот:
А В 1 - знакомы 2- не знакомы
1-мужской 5,63 5,08
2- женский 5,43 4,87
Найдем параметры логлинейной модели по формулам (4.5):
u
0
= 5,255; u
1
b
= 0,1; u
1
a
= 0,28; u
11
ab
= 0.
39
Найдем значение Х
2
инф
по формуле (4.4):
Xnnnnnnn
Iijijii
iji
jj
j
2
2
=−−+
∑∑∑∑
(ln ln lnln
** * * ***
2
n
)
*
−
.
X
I
2 298 298 142 142 210 210 150 150
508 508 292 292 440 440 360 360
800 800 7 52.
=⋅+⋅+ +⋅
−⋅ −⋅ −⋅ −⋅ +
+⋅ =
(ln ln ln ln
ln ln ln ln
ln ) ,
Число степеней свободы для этой модели равно
ν
= 4 – 3 =1 (число
клеток минус число параметров модели).
По таблице распределения хи-квадрат находим
Х
2
крит
(
ν
= 1;
α
=0,05) = 3,841.
Так как Х
2
I
> Х
2
крит
, то модель независимости неадекватна.
Дальнейшее ее упрощение не имеет смысла. Однако в целях дальнейшей
иллюстрации проведем остальные расчеты.
3. Модели с отсутствием влиянием одного фактора.
Модель с отсутствием влияния фактора В:
ln
*
nuu
ij i
a
=+
0
.
Рассчитаем теоретические частоты, получим таблицу:
А В 1- знакомы 2 - не знакомы n
i*
1-мужской 220 220 440
2- женский 180 180 360
n
*j
400 400 800
Таблица логарифмов теоретических частот:
А В 1 - знакомы 2 - не знакомы
1-мужской 5,39 5,39
2- женский 5,19 5,19
Параметры логлинейной модели: u
0
= 5,29; u
1
b
= 0; u
1
a
= 0,1;
u
11
ab
= 0.
Для этой таблицы критерий Х
2
инф
= 66,577.
4. Модель с отсутствием влияния фактора А:
ln
.
*
nuu
ij j
b
=+
0
40
