Tong W. Wind Power Generation and Wind Turbine Design

Подождите немного. Документ загружается.

Tower Design and Analysis 535

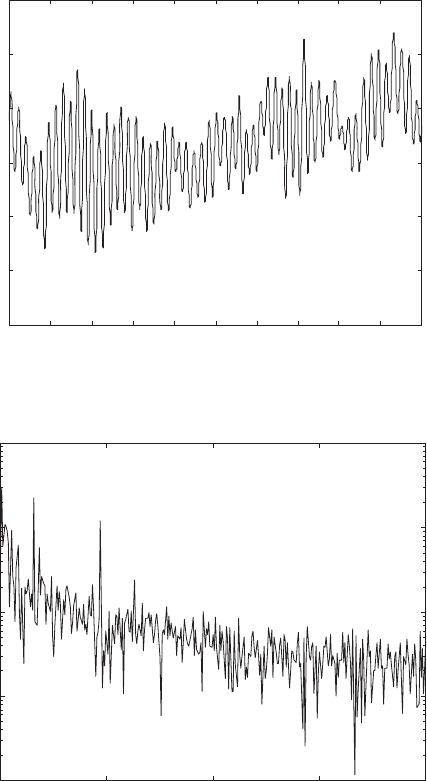
the blades masses are lumped on the top of the tower thus, ignoring the tower–blade

interaction. The maximum observed tower tip response is 0.108 m.

The forced vibration response of the coupled tower–blade model is also calcu-

lated for a rotational frequency of 1.57 rad/s. Figure 4 presents a Fourier transform

of the simulated ﬂ uctuating wind velocity acting at the tip of the blade. An increase

in energy is clearly observable at integer products of the rotational frequency.

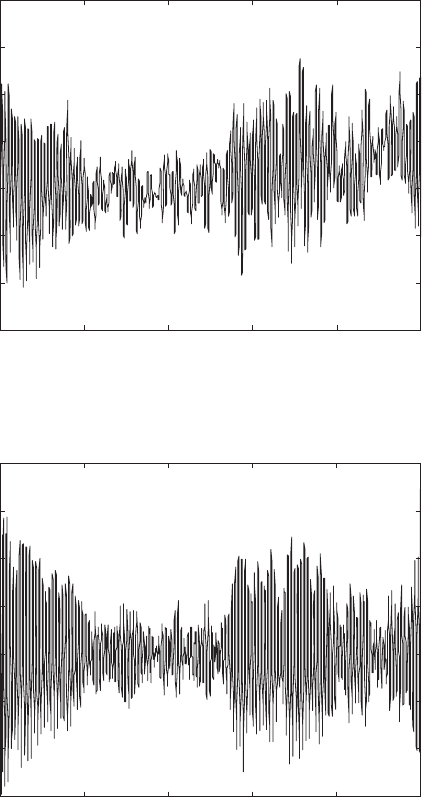
Figure 5 illustrates the computed blade tip displacement time-history. The maxi-

mum observed displacement is approximately 0.75 m. Figure 6 presents the total

0 10 20 30 40 50 60 70 80 90 100

0.02

0.04

0.06

0.08

0.1

0.12

Time (s)

Total Response (m)

Figure 3: Displacement time-history at the top of the tower ignoring blade rotation.

0 5 10 15 20

Frequency (rads

-1

)

Fourier Amplitude

Figure 4 : Fourier transform amplitude of wind velocity.

536 Wind Power Generation and Wind Turbine Design

base shear time-history due to the forced vibration of the three rotating blades.

A maximum base shear force of nearly 150 kN is observed. The three rotating

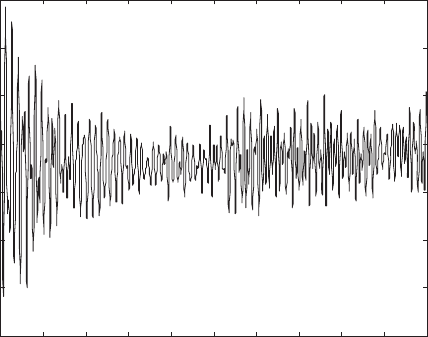
blades are now coupled to the tower-nacelle and the maximum tower tip displace-

ment response is found to be 0.385 m, as presented in the displacement time-

history in Fig. 7 . Thus, inclusion of blade–tower interaction results in a 256%

increase in peak tip displacement of the tower compared to the case excluding

blade–tower interaction.

0 20 40 60 80 100

-0.4

-0.2

0.2

0.4

0.6

0.8

Time (s)

Total Response (m)

Figure 5: Blade tip displacement time-history.

0 20 40 60 80 100

-1.5

-1

-0.5

0.5

1.5

x 10

Time (s)

Total Base Shear (N)

Figure 6: Base shear time-history.

Tower Design and Analysis 537

In the approach by Murtagh et al. [ 30 ], the coupled system equation of motion

is primarily cast in the frequency domain via Fourier transform. This allows the

coupling of the tower and the blades. The time domain along-wind response of the

coupled assembly is ultimately obtained by inverse Fourier transform. There are a

number of merits behind this type of approach. The technique is relatively simple,

especially compared with a more computationally expensive ﬁ nite element formu-

lation. The approach may be used in a preliminary quantitative design, which may

subsequently be validated by a more rigorous analysis. The dynamic properties of

the coupled system are available using the dynamic properties of each of the two

sub-systems, which is an extension of the substructure synthesis approach.

3 Design of tower

A complete dynamic analysis of the tower taking into account the effect of the rota-

tion of the blades (rotors) and the nacelle mounted at the top is necessary for ensuring

the safety and operational serviceability. However, such a detailed dynamic analysis

may be time consuming and rigorous at a preliminary design stage when the initial

conﬁ guration has to be chosen based on the design forces and displacements. Hence,

for an initial assessment it may be more attractive to use an approximate simpliﬁ ed

approach while taking account of the stochasticity in the wind loading (and hence in

the response of the tower) and the rotor–tower interaction.

Gust response factor (GRF) approach is a simple technique used by struc-

tural engineers in the along-wind design of ﬂ exible structures and incorporates

the stochastic and dynamic effects. This technique is now well developed due

to the contributions of Davenport [ 38 ] and Velozzi and Cohen [ 39 ]. GRF is the

ratio of the maximum or peak response quantity to the mean response quantity.

0 10 20 30 40 50 60 70 80 90 100

-0.3

-0.2

-0.1

0.1

0.2

0.3

0.4

Time (s)

Total Response (m)

Figure 7 : Displacement time-history at the top of the tower with blade interaction.

538 Wind Power Generation and Wind Turbine Design

Hence, when this factor is applied to the responses from the mean wind loading,

it yields the maximum design values.

The methodology developed by Davenport and, Velozzi and Cohen calculated

the GRF using a ratio of displacements, and while this yielded accurate maximum

expected response for displacement, it was found to fall short in providing esti-

mates of other response parameters, such as bending moment and shear force.

Following the work by [ 38 , 39 ] several new models of the GRF have been pro-

posed by Holmes [ 40 ] and Zhou and Kareem [ 41 ], with the latter being based on

base bending moment, rather than displacement. The GRF methodology has also

become the basis of most modern design codes worldwide [ 42 ].

3.1 Gust factor approach

The traditional Davenport-type GRF assumes that the ﬂ exible structure may be rep-

resented by a single degree-of-freedom (SDOF) representing the fundamental mode

of vibration, and this is usually sufﬁ cient. However, if a structural system like a

wind turbine tower (with coupled tower–rotor interaction) has more than one mode

contributing to the response, the traditional GRF methodology may yield inaccurate

representations of the energy contained in the response. Thus an extension of the

traditional GRF methodology to include the effects of higher modes in the derivation

of the GRF is required for application in the case of a wind turbine tower.

A GRF for evaluating the along-wind response of wind turbine towers has been

proposed by Murtagh et al. [ 43 ]. The approach presented differs from the conven-

tional GRF methods as the GRF contains contributions from two resonant modes,

mainly due to rotor blade–tower interaction effects. The wind turbine tower model

considered contains two inter-connected ﬂ exible sub-systems, representing the

tower and a three-bladed rotor system. It is assumed that all the blades vibrate

identically in the ﬂ apwise mode (out-of-plane) coupled with the tower. Each com-

ponent is initially modelled as a separate degree-of-freedom (DOF) and these are

coupled together to form an equivalent reduced order model of the coupled tower–

rotor system considering the ﬁ rst two dominant modes. Thus, the resonant compo-

nent of the response contains energy output from the two modes of the coupled

system. This is an approximate way to account for the effect of the blades fed back

to the tower including the coupled tower–blade interaction. The GRF is obtained

for both tower tip displacement and base bending moment through numerical

integration, with a closed form expression included for the former.

3.2 Displacement GRF

The displacement GRF [ 43 ], G

DISP

, is obtained as a ratio of the expected maxi-

mum displacement response, X

MAX

( t ) divided by the mean displacement, x , with

the latter being represented by the equation:

CS,1-TT D,1 CS,2-TT D,2

CS,1 CS,2

ΦΦ

(10 )

Tower Design and Analysis 539

with Φ

cs, j –TT

( j = 1, 2) being the j th coupled system (CS) mode shape component

at the top of the tower,

CS, j

K is the j th modal stiffness of the coupled system and

D, j

is the j th modal mean drag force. Because modal/generalized quantities are

used in eqn ( 10 ), it is assumed that the free vibration parameters obtained from the

tower–rotor system are from a classically damped one. The modal mean drag force

on a structure (i.e. the tower or the blade) is obtained as

D, D CS,

() ()() ()d

fCzBzvzzzr

⎛⎞

=Φ

⎜⎟

⎝⎠

∫

(11 )

where H is the length over which drag is to be calculated (i.e. the total height of the

tower or the length of the blade), C

( z ) is the drag coefﬁ cient, B ( z ) is the width of

the tower (or blades), and ()vz is the mean wind velocity and Φ

CS,j

( z ) is the j th

mode shape component of the coupled system, all as a function of the spatial vari-

able z . The expected maximum displacement may be obtained as the product of a

peak factor, Ψ (using ﬁ rst passage analysis, as in [ 44 ]) and the root mean square

(RMS) of the displacement response at the top of the tower, s

. This RMS dis-

placement response, which includes a second mode of vibration, may be obtained

by taking the square root of the area under the displacement response PSD func-

tion, S

( f ) The PSD function S

( f ) is found as the sum of the products of the

modal wind drag force PSD functions with their appropriate squared amplitude of

the modal mechanical admittance functions [ 43 ].

The modal drag force PSD function may be obtained from the expression:

MF MF VV D 1 D 2 1 2 1 2

CS, 1 CS, 2 1 2 1 2

() () () ()()()()()

() ()(, ;)dd

S f S f CzCzBzBzvzvz

zzRzzfzz

∫∫

(12)

where S

( f ) denotes the wind velocity PSD function at the top of the tower [ 37 ],

r is the density of air, and R ( z

, z

; f ) is the spatial coherence function between

elevations z

and z

[ 19 ]. The mechanical admittance function at the top of the

tower due to a unit force at that point for the j th mode may be obtained as

CS, TT CS,

22 2

CS, CS, CS, CS, CS,

()

4 1 (/ ) 2 (/ )

jj j j j

fM ff i ffx

−

⎡⎤

−+

⎣⎦

(13 )

where F

CS, j

is the j th modal force due to a unit force placed at the top of

the tower, f

CS, j

is the j th natural frequency,

CS, j

M is the j th modal mass

CS, 0 CS,

(()()d)

Mmzzz=∫ Φ

with m ( z ) as the mass distribution of the structure

and, x

CS. j

is the j th modal damping ratio.

Two procedures have been proposed by Murtagh [ 43 ] based on how the value of

. may be calculated. It may be computed by numerically evaluating an integral

or it may also be obtained in closed form based on some approximation. For the closed

form calculation, a method of decomposition can be employed, in which it is assumed

that the variance of the displacement response PSD function may be separated into

two components: a background component and a resonant component. Contrary to

540 Wind Power Generation and Wind Turbine Design

the conventional GRF approach, in the proposed methodology [ 43 ], there are two

contributions for the resonant component. The square of the non-

dimensionalized form of background component of the gust factor

can be

expressed as

222 222

CS,1 TT CS,1 CS,2 CS,2 CS,2

B MF1MF1 MF2MF2

44 2 2 44 2 2

CS,1 CS,1 CS,2 CS,2

()d ()d

16 16

GSffSff

fMx fM x

∞∞

−−

ΦΨ Φ Ψ

ππ

∫∫

( 14 )

The integral in eqn ( 14 ) may be evaluated numerically, or by assuming the

integrand to be a white noise, or from a known value of turbulence intensity.

The resonant component of the gust factor comprises of two non-dimensionalized

terms representing contributions of the ﬁ rst and second modes of vibration,

R,1

and

R,2

, respectively. These terms are given by the expressions:

22 2

CS, -TT CS, MF MF CS,

33 2 2

CS,j CS,j CS,j

()

=,=1,2

64p f M x x

jjjjjj

ΦΦ Ψ

(15 )

where Ψ

is the peak factor associated with mode ‘ j ’. Thus, the closed form solution

for the displacement GRF, G

DISP-CF

, is obtained as

22 2

DISP CF B R,1 R,2

1GGGG

−

=+ + +

(16 )

where G

and G

R, j

represent the background and resonant components of the

displacement GRF, respectively.

3.3 Bending moment GRF

A GRF also has been derived based on the bending moment GRF [ 41 ] at the tower

base, G

by [ 43 ] which is presented for comparison. Similar to the displacement

GRF, G

will contain contributions from two modes of vibration and is obtained

as the ratio of the expected maximum base bending moment, Y

MAX

( t ) (= Ψ s

to the mean base bending moment,

( 0.5 () ()() d).

yCzBzvzzzr∫

The RMS of

the base bending moment, s

, is obtained from the equation:

1/2

BM MF MF D,

() ()d

jjj j

SfHffs

∞

⎛⎞

=Γ

⎜⎟

⎝⎠

∑

∫

(17 )

where

Γ is given by

CS, CS,

(2 ) ( ) ( ) d

jj j

fmzzzzΓ= π Φ

∫

(18 )

The base bending moment GRF, G

may be obtained as

=+Ψ

(19 )

Tower Design and Analysis 541

A series of numerical examples are presented from [ 43 ] to investigate the

magnitude of GRFs obtained for the model which allows for blade–tower interac-

tion, and these are compared with GRF values obtained from an equivalent SDOF

model which ignores blade–tower interaction by lumping the mass of the blades in

with that of the nacelle. A tower (steel) of height 50 m with rotor (GFR epoxy)

diameter of 60 m is considered with the details available in [ 43 ]. Four different

rotational frequencies of the rotor blades were considered. As rotational frequency

of the blades increases, the fundamental frequency of the blades also increases,

and this leads to increase in the natural frequencies of the coupled systems.

Tables 1 and 2 show the GRFs obtained for the lumped mass equivalent SDOF

and two DOF tower–blade interaction models for a mean wind velocity of 20 m/s

at the top of the tower. A time of 600 s was used to obtain the GRFs, as used in

Eurocode 1 (CEN 2004) [ 45 ]. Included in these tables are the displacement GRFs

obtained by numerical integration and in closed form, G

DISP-NI

and G

DISP-CF

respectively, and the base bending moment GRF obtained using numerical integra-

tion, G

BM-NI

. It may be noted that the second mode affects the background and the

resonant components and changes the response obtained from the classical gust

factor approach.

It is evident from Tables 1 and 2 that the choice of modelling strategy, i.e.

lumped mass SDOF or two DOF blade/tower interaction, has a bearing on the

magnitudes of both the displacement and base bending moment GRFs obtained.

When the blades are stationary ( Ω = 0 rad/s) in the two DOF case, the values of

DISP-NI

and G

BM-NI

obtained differ from the SDOF model values of G

DISP-NI

and

BM-NI

by over 10 and 8%, respectively. These differences remain nearly constant

until the case of Ω = 3.14 rad/s where they are equal to 5 and 8%, respectively.

The values of G

DISP-NI

and G

DISP-CF

showed a close match in most cases, though

it was observed that when the two modes were closest together ( Ω = 0 rad/s),

Table 1: GRFs for SDOF lumped mass model.

DISP-NI

2.275

DISP-CF

2.291

1.019

R,1

0.792

BM-NI

2.429

Table 2: GRFs for coupled model with blade–tower interaction.

Ω (rad/s)

DISP-NI

DISP-CF

R,1

R,2

BM-NI

0.000 2.507 2.356 1.032 0.850 0.268 2.633

0.785 2.509 2.370 1.044 0.837 0.266 2.599

1.570 2.503 2.392 1.070 0.833 0.257 2.506

3.140 2.381 2.327 1.059 0.753 0.170 2.225

542 Wind Power Generation and Wind Turbine Design

DISP-CF

yielded a difference of 6% from G

DISP-NI

. The difference in the value

dropped to less than 1% when the modes move further apart at Ω = 3.14 rad/s. It

was also observed from Tables 1 and 2 that the displacement and bending moment

GRFs obtained showed some disagreement, with the values of G

BM-NI

being higher

than those of G

DISP-NI

. The largest disagreements were observed at the single DOF

model and the two DOF model case of Ω = 0 rad/s, where differences of 7 and 5%

were observed.

4 Vibration control of tower

As the wind turbines grow bigger in size and become ﬂ exible with the increase in

rotor diameter, it is not only enough to estimate the design forces and ensure the safety

of the wind turbine. Additionally, it is necessary to control the vibration response of

the ﬂ exible wind turbine tower. It has been observed that wind-induced accelerations

may be the reason for the unavailability of wind turbine with increased downtime and

may cause damage to the acceleration sensitive subcomponents and devices in a wind

turbine [ 46 ]. Hence, it is important to consider structural vibration control strategies

for wind turbine towers for operational reliability of wind turbines.

Vibration control strategies for ﬂ exible and tall structures susceptible to large

wind-induced oscillations in general are becoming increasingly important, partic-

ularly with the current tendency to build higher and lighter. HAWTs are no excep-

tion, having experienced a dramatic increase in scale in the past decade. This is

particularly evident in offshore wind turbines, with rotor diameter measuring over

120 m. As the design approach is based on strength considerations, stiffness does

not increase proportionally with increase in height and these ﬂ exible turbines may

experience large-scale blade and tower deformations having non-linear character-

istics, which may prove detrimental to the functioning of the turbine. Thus, there

is distinct merit in investigating the vibratory control of both wind turbine blades,

e.g. using blade pitch [ 47 , 48 ] and towers [ 49 ], using an external energy damper.

Among the several structural vibration controllers available, tuned mass damper

(TMD) as a passive vibration control device has become popular. It suppresses

vibration by acting as an energy dissipator. Considerable amount of literature now

exists on the use of TMDs for ﬂ exible structures [ 50– 52 ]. Use of a TMD for sup-

pression of vibration in a wind turbine tower including blade–tower interaction has

been studied by Murtagh et al. [ 49 ]. They provided a simple analytical framework

in order to qualitatively investigate the effect of a TMD on the fore-aft response of

a wind turbine tower.

4.1 Response of tower with a TMD

The displacement response of a wind turbine tower including blade–tower interac-

tion and rotationally sampled turbulence acting on the rotor blades, and with an

attached TMD may be expressed as [ 49 ]:

DAMP

TT TTB

[ ]{ ( )}+[ ]{ ( )}+[ ]{ ( )} = { ( )}+{ ( )}+{ ( )}Mxt Cxt Kxt Ft Vt F t

 

(20 )

Tower Design and Analysis 543

where [ M

], [ K

] and [ C

] are the mass, stiffness and damping matrices of the

tower/nacelle, respectively, {()},{()},{()}xt xt xt



are the time-dependent displace-

ment, velocity and acceleration vectors respectively, { F

( t )} is the total wind drag

loading acting on the tower,

{()}Vt

′

is the effective blade base shear acting at

the top of the tower and { F

DAMP

( t )} is the damping force brought about by the

action of the TMD. Details on how to calculate the effective blade base shear

time-histories and total wind drag loadings may be found in Murtagh et al. [ 30 ].

The response time-histories of the tower can be obtained following a modal

decomposition of the tower response, transforming the set of equations in eqn ( 20 )

in a Fourier domain and subsequently applying an inverse FFT [ 49 ].

4.2 Design of TMD

For designing a TMD two important parameters need to be considered, the damp-

ing ratio and the tuning ratio. For an efﬁ cient performance of a TMD these two

ratios need to be optimized.

A number of approximate and empirical expressions are available for the evalu-

ation of the optimum damping ratio of the TMD. Given below is the simple

expression by Luft [ 51 ] for the optimum damping ratio of the TMD:

,opt

x =

(21 )

where m is the mass ratio of the damper (i.e. mass of the damper to the entire

mass of the assembly). In order to tune the damper, its natural frequency is

obtained as the product of a tuning ratio n , times the natural frequency of the

coupled tower–blades system, i.e.:

CS,1

(22 )

where w

CS,1

is the fundamental frequency of the coupled tower-rotating blades

assembly. It is possible to derive a closed form expression for the optimum tun-

ing ratio of the TMD attached to a damped structure based on the “ﬁ xed- point”

theory of Den Hartog [ 53 ] which had been proposed for the case of undamped

structural systems subjected to sinusoidal excitation. In the optimal design of a

TMD attached to an undamped structural system subjected to sinusoidal excitation

[ 53 , 54 ], two “ﬁ xed-point” frequencies were obtained at which the transmissibil-

ity of vibration is independent of the damping in the TMD. It was also observed

that the amplitude of the response transfer functions at the two ﬁ xed points was

unequal and had a contrasting effect with the change in the tuning ratio. For a

structure subjected to an external force which has wide banded energy content or

which has dominant energy at the natural period of the structure, the maximum

response reduction is achieved when the area under the transfer function curve

is at a minimum. This implies that the values of the transfer function at the ﬁ xed

points should be equal and the value of the tuning ratio for which this occurs is the

544 Wind Power Generation and Wind Turbine Design

optimal tuning ratio of the TMD. Ghosh and Basu [ 55 ] extended the theory based

on “ﬁ xed-points” to obtain closed form expression for optimal tuning ratio in case

of a damped structure. This was used by Murtagh et al. [ 49 ] designing an optimal

TMD for a wind turbine tower. The expression for the optimal tuning parameter

opt

for a wind turbine tower with damping ratio x

in the fundamental mode of

vibration is [ 49 , 55 ]:

14 (2 1)

opt

(1 )

xmx

−− −

(23 )

The optimal tuning ratio together with an optimal damping ratio in the TMD will

minimize the maxima of the displacement transfer function of a wind turbine tower.

Murtagh et al. [ 49 ] considered a tower of hub height 60 m and blades with

radius 30 m for a three-bladed wind turbine and designed a TMD for suppression

of the tip displacement. The mean wind speed at the top of the tower was assumed

to be 20 m/s. The ﬁ rst three modal damping ratios of the tower were assumed to be

1% of the critical. A mass ratio of 1% was assumed for the TMD, giving the

damper a damping ratio of 5% of critical. Thus, when used in conjunction with eqn

( 23 ), an optimal tuning ratio of 0.99 is obtained. The forced vibration responses of

the coupled tower–blades model including and excluding the TMD were calcu-

lated and compared. Two rotational frequencies of the rotor system were consid-

ered, and the blades are perturbed under the action of rotationally sampled wind

turbulence [ 30 ]. The design parameters of the dampers designed for the two cases

are presented in Table 3 .

Figure 8 presents the tip displacement transfer function amplitudes obtained for

the coupled tower and rotating blades model ( Ω = 15 rev/min) with and without

the damper. When contrasting the two transfer functions obtained, it is evident that

the presence of the damper causes the peak to split and decrease substantially in

magnitude. Figure 9 presents the simulated wind-induced response of the coupled

blade–tower model, at the top of the tower, including and excluding the damper.

From this ﬁ gure, it is evident that the damper has been effective in suppressing the

vibrations, particularly in the earliest portion of the time-history, where the

Table 3: Properties of the TMD.

Rotational frequency (rev/min)

15 30

Mass ratio (%) 1 1

Tuning ratio 0.99 0.99

Natural frequency (rad/s) 4.45 4.55

Mass (kg) 997 997

Stiffness constant (kN/m) 20.64 19.74

Damping constant (kNs/m) 0.45 0.44

Damping ratio (%) 5 5