Тевяшев А.Д., Литвин О.Г. Вища математика. Загальний курс: Збірник задач та вправ

Подождите немного. Документ загружается.

б) Будуємо граничні прямі, що відповідають даним нерівностям :

/, : -х,+х

= 6, Лі(0,6)є/,, Л

(-6,0)є/, ;

: Зх,+5х

-=15, 5,(0,3)є/

, й

(5,0)є/

;

: х

= 1 .

Область розв'язків першої нерівності містить початок координат, дру-

гої і третьої нерівностей - не містить початку координат (координати точки

О (0, 0) не задовольняють другій і третій нерівностям).

Стрілками позначені півплощини, точки яких задовольняють не-

рівностям . Областю розв'язків є опукла многокутна необмежена область

фис.

1.3).

в) Будуємо граничні прямі :

/, : Зх,-2х

=-6 , А

(0, 3)є/, ,

і, Д,(0,1)є/

•

х, + 5х

х, =

(-2.0)є/, ;

(-5,0)є/

;

0 ,

/4 : х

= 0 .

Будуємо область розв'язків кожної нерівності.

Не існує жодної точки, загальної для всіх півплощин, що відповідають

даним нерівностям (рис. 1.4).

Отже, область розв'язків порожня . Система нерівностей несумісна .

Рис.

1.2

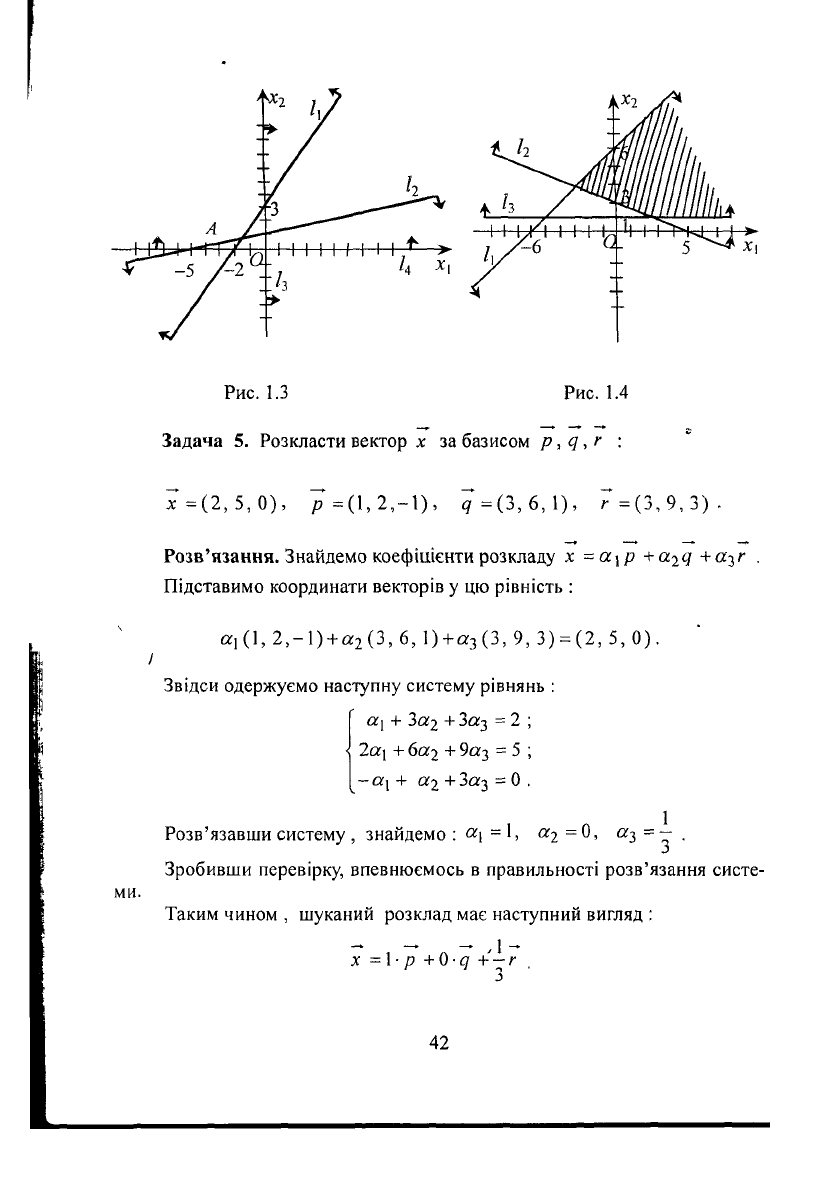
Рис.

1.3 Рис. 1.4

Задача 5. Розкласти вектор х за базисом р, д, г :

х=(2,5,0), 7 = (1,2,-1), ?=(3,6,1), Г = (3,9,3).

Розв'язання. Знайдемо коефіцієнти розкладу х =а

р +а

о +сс^г .

Підставимо координати векторів у цю рівність :

(1,2

-1) + а

(3,6,1) + аз(3

3) = (2

5,0).

Звідси одержуємо наступну систему рівнянь :

а, + За

+3«з = 2 ;

2а\

6а

9а

= 5 ;

а.\

+ а

За

= 0 .

Розв'язавши систему , знайдемо: «і =1. «2

0' ^3

^ •

Зробивши перевірку, впевнюємось в правильності розв'язання систе-

ми.

Таким чином , шуканий розклад має наступний вигляд :

х =і- р + 0

•

— г

ГЛАВА

2. ВИЗНАЧНИКИ І МАТРИЦІ.

СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ

[І,

гл . І, § І.І -1.20 ; гл . 2, §2.1 - 2.7]

2.1. Визначники і матриці

Визначником п -го порядку називають число, що позначається

«ІЛ

п\

п2 •••

пп

: дорівнює алгебраїчній сумі пі членів. Кожний член визначника дорівнює

добутку п елементів визначника, що взяті по одному з кожного рядка і кожно-

го стовпця визначника. Знак члена рівний (-І)',де і - число інверсій в пере-

становці других індексів елементів, якщо перші індекси записані в натураль-

ному порядку.

Мінором М

елемента а

визначника називається визначник

(п-ї)-

го порядку, отриманий з даного визначника шляхом викреслення рядка і сто-

впця, на перетині яких стоїть даний елемент.

Алгебраїчним доповненням елемента а

і}

визначника називається

число

Ау=(-ї)'^М

Одним з основних методів обчислення визначників п-го порядку є

метод пониження порядку, оснований на теоремі розкладання, що зводить

обчислення визначника до обчислення визначників другого і третього по-

рядків. При цьому використовуються й інші властивості визначників .

Теорема розкладання :

^=\

або

= Ц

и >

/=і

Д =

а,, а

«21 «22

Матрицею розміру тхл називається таблиця чисел а

/' = 1, т , ]=\,п , вигляду

' а

... а,„'

22 •••

2п

А =

т\

т2

•••

тп

Коротко :

тхп

, (а

) „, „ .

Сумою А + В матриць А-{а

)

тп

і В ={Ьу)

тп

називається мат-

риця С=(с

)

тп

,така, що с

-=а

+Ь

Добутком а А матриці А

(а

)

„ на число а називається матриця

С=(Су)

тп

,така, що с

=аа

Добутком АВ матриці А=(а

)

т п

на В=(Ь

) „ / називається мат-

риця С=(с

)

т>і

,де

=2>/А

к)

т ,

7 =

тобто елемент с

дорівнює сумі добутків відповідних елементів /-го рядка

матриці А і і -го стовпця матриці В.

Степенем к матриці А називається матриця

С = А

=А-А-...-А ,

раз

де к - ціле додатне число ; А

= Е

•

Многочленом від матриці А називається вираз, що має вигляд

Р(А) =

+а

...

]

Е ,

де к - ціле додатне число , А® = Е.

Оберненою до квадратної матриці А називається матриця А~

така,

що А-А'

=А~

•

А = Е .

Формула для знаходження оберненої матриці:

•21

•лі

*22

*л2

\п

2п

деіА

А 22

2п

п\

п2

УЇМ

Рангом матриці називається найвищий з порядків її мінорів, відмінних

кд нуля. Позначення К&А . Відмінний від нуля мінор матриці А , порядок

того г = К.§ А , називається базисним мінором .

Елементарні перетворення матриць :

1) перестановка рядків (стовпців);

2) множення рядка (стовпця) на число , відмінне від нуля ;

додавання до елементів рядка (стовпця) відповідних елементів іншого

•ча

(стовпця), помножених на деяке число .

Елементарні перетворення не змінюють рангу матриці. На цьому ба-

5>ється метод елементарних перетворень для знаходження рангу .

Приклад 1. Задані матриці :

1 2

-10 4

ґ-2 3^

с =

5 8 -1 2

,-1 \

"4,

Чи можна додати матрицю А до матриці В1 Матрицю А до матриці С?

Знайти А + С ; 2А-ЗС + В •

Розв'язання. Матрицю А не можна додати до матриці В , бо матриця А

має розміри 3x2 , матриця В - розміри 2x3 , а додавати можна матриці

однакових розмірів . Матриці А і С мають однакові розміри , отже , їх можна

додавати .

Враховуючи , що при додаванні матриць додаються відповідні елемен-

ти , маємо

С-

Оскільки множення матриці на число є операція , яка полягає в тому ,

що кожний елемент матриці помножується на це число , то

ґ-2

' 0

3 -1

8 8

1° Ь

\ І-

]

ґ-2

2 А

2 -1

6 -2

-ЗС = (-3)

5 8

15 -24

,°

1°

-9,

Отже,

]

' 13

2 Л-3 С +

£>

= 6

-24

-1

-10

-24

,°

-9)

-5,

Приклад 2. Задані матриці:

1 -1 3^

0 2 4

1-12 0

5 7 9 -1

З 4 5 15

Чи існує добуток : АВ ; &4 ?

Розв'язання. Оскільки матриця А має розміри 2x3 , а матриця і?-

розміри 3x4 , то число стовпців матриці А дорівнює числу рядків матриці В ,

отже , А В існує . Число стовпців матриці В не дорівнює числу рядків мат-

риці А , отже , ВА не існує .

Приклад 3. Задані матриці

ґ-1 2 4

5 6 7

0 3-1,

А =

1 0 -2

3 9-5

С = 2

Знайти АС ; /15 .

Розв'язання. Використовуючи означення добутку матриць , знаходимо

(\\

АС-

(\ 0 -2

3 9-5

Ь1 + 0-2 + (-2)-3

• 1

+ 9

•

2 + (-5)

• З

АВ

Г1 0 - 2

З 9 -5

'•12 4

5 6 7

О 3 -1

'і-(-1) + 0-5 + (-2)-0

1 •

2 + 0

6 + (-2)

3 1-4 + 0-7 + (-2)-(-Гр

3-(-1) + 9-5 + (-5)-0 3-2 + 9-6 + (-5)-3 3-4 + 9-7 + (-5)-(-І),

(-\ _

42 45 80

Приклад 4. Показати, що матриця А =

/(х)

х -Зх

+ 5

'2 -1

З 1

є коренем многочлена

Розв'язання. Підставимо в даний многочлен замість х матрицю А ,

тоді отримаємо

ДА)= А

-ЗА + 5Е =

'2 -О

2 -1

+ 5

1 0

0 1

'1 -ЗЇ

°1

,9 -2,

-з,

,о

5у

Отже , матриця А є коренем даного многочлена .

Приклад 5. З'ясувати , чи існує матриця , обернена матриці

(\ -1 2^

А=

1 1-2

1 1 4,

і якщо існує, знайти її. Виконати перевірку : А

•

А = Е.

Розв'язання. Оскільки сієї

= 12^0 , то існує обернена матриця А

що може бути знайдена за формулою

-1

А~

йеіА

Лзі

А 22

^32

А 23 Лзз

де А

- алгебраїчне доповнення елемента

Оскільки

= 6,

-2

:-6,

'13

1 1

= 0,

2\=-

1 2

1 4

= 6,

^22 =

1 2

1 4

2, Л

-1

1 1

= -2,

то

1 =

-1

:0,

-2

= 4, Л

/4"'

-6

6 0

2 4

-2 2

і.

Перевіримо правильність матриці А :

1 -1

1 1

АА~

=±-

1 2

1 -2

1 4

V 6

-6

6 0^

2 4

-2 2

Гі2 0 0^

0 12 0

0 0 12

1 0 0

Приклад 6. Використовуючи означення рангу матриці , знайти ранг

матриці А :

'10 2 -Г

А= 3 0 1 2

4 0 З 1,

Розв'язання. Серед мінорів першого порядку є відмінний від нуля , бо

матриця А ненульова . Серед мінорів другого порядку є також відмінні від

-5*0 - Всі мінори третього порядку дорівнюють

нуля , наприклад

З 1

нулю (перевірте). Отже, К§ А = 2 .

Приклад 7. Використовуючи метод елементарних перетворень , знай-

•н ранг матриці А :

Розв'язання.

1 -1

5 1

4 1

10 1

1 2

10 6 6

+(-5) 5,

+(-4) 5,

+(-10) 5,

-1

3 -13 -19

-11

-15

10 -24

-36

-К-1)

-«-1)-5з

-к-1)-5

1 -1

0 1

0 5

0 0

2 3 4

4 -2 -4

-7 -11 -15

0 0 0

-К-5)-5

1-12 3 4

0 1 4-2-4

0 0 -27 -1 5

0 0 о о о;

Отримали трапецієподібну матрицю, ранг якої дорівнює 3. Звідси

Л§Л = 3.

2.2. Системи лінійних алгебраїчних рівнянь

Система лінійних алгебраїчних рівнянь має вигляд

а,

]

х, + а|2 х

+ •••

+ Я]„ х„ = Ь\ ;

«21

\ +«22*2 + --- + «2л*л =*2 і

«ті

1 +«/«2*2 + ••• + «лет *п =Ь

ібо в матричній формі:

АХ = В ,

ДЄ

А =

«11 «12

«21 «22 «2л

т\

«ті ••• «тп

(Х[

]

; х

; в =

)

Розширена матриця системи має вигляд

А = (А\В) =

«11 «12

«21 «22

«ші

т2

2п

Згідно з теоремою Кронекера - Капеллі, для того щоб система рівнянь

була сумісна, необхідно і достатньо , щоб К§ А = К§ А .

При цьому , якщо К&А = К§А=п, п

—

число невідомих , то система

має єдиний розв'язок ; якщо К§ А = К§ А = г < п , то система має безліч роз-

в'язків ; якщо К§ А * К§ А , то система несумісна .

Розглянемо деякі методи розв'язування систем .

Матричний метод: Х =

А~

-В.

Реалізація методу полягає в знаходженні оберненої матриці і множенні

її на стовпець вільних членів. Використовується для невироджених (сієї А * 0)

квадратних систем .

А,

Формули Крамера : х,

/ = 1, п, де Д = сІесЛ

0 - визначник

системи ; Д

(

одержується з Д шляхом заміни / -го стовпця стовпцем вільних

членів . Також використовується для невироджених квадратних систем .

Метод Гаусса грунтується на наступній теоремі: елементарним пере-

творенням рядків розширеної матриці системи відповідає перетворення ціє:

, системи в еквівалентну.

З допомогою елементарних перетворень рядків розширеної матриці,

а також переміни місцями стовпців, що відповідає перепозначенню змінних.

матриця А зводиться до східчастої (або трикутної) форми. Цій матриц;

ставиться у відповідність система, еквівалентна вихідній. Це прямий хіл

методу Гаусса. Розв'язання отриманої системи здійснюється знизу уверх