Taylor M.E. Partial Differential Equations III: Nonlinear Equations
Подождите немного. Документ загружается.

398 15. Nonlinear Parabolic Equations
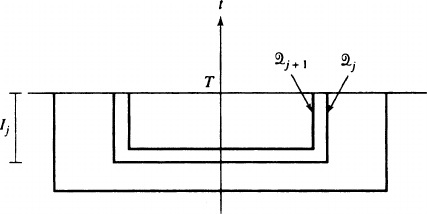
FIGURE 9.1 Setup for Moser Iteration
In view of (9.5), an example is
(9.10) v D
1 C u
2
1=2
;Lu D 0:
We will obtain such an estimate in terms of certain Sobolev constants, .Q
j
/ and
C
j
, arising in the following two lemmas, which are analogous to Lemmas 9.1 and
9.2 of “14.”
Lemma 9.1. For sufficiently regular v defined on Q
j
, and with n=.n 2/,
we have
(9.11)
kv
k
2
L
2
.Q
j
/
.Q
j
/
j
.v/
1
kr
x
vk
2
L
2
.Q
j
/
C
j
.v/
;
j
.v/ D sup
t2I
j
kv.t/k
2
L
2
.
j
/
:
Proof. This is a consequence of the following slightly sharper form of (9.10)
in “14”:
(9.12) kv
k
2
L
2
.
j
/
.
j
/
kr
x
vk
2
L
2
.
j
/
kvk
2.1/
L
2
.
j
/
Ckvk
2
L
2
.
j
/
:
Indeed, integrating (9.12) over t 2 I
j
gives (9.11).
Next, we have
Lemma 9.2. If v>0is a subsolution of @
t
L, then,
(9.13) kr
x
vk
L
2
.Q
j C1
/
C sup
t2I
j C1
kv.t/k
L
2
.
j C1
/
C
j
kvk
L
2
.Q
j
/
;
where C
j
D C.Q
j
;Q
j C1
/.
Proof. This follows from (9.8), with u D v,ifweletT
1
D
j
,pick D
'
j
.x/
j
.t/, with '
j
.x/ D 0 for x near @
j
, while '
j
.x/ D 1 for x 2
j C1
,
and
j
.
j
/ D 0, while
j
.t/ D 1 for t 2 I
j C1
.ThenletT
2
run over Œ
j C1
;T.

9. Quasi-linear parabolic equations III (Nash–Moser estimates) 399
We construct the functions '
j
and
j
to go from 0 to 1 roughly linearly, over
a layer of width Cj
2
.Asin(9.12) of “14,” we can arrange that
(9.14) .Q
j
/
0
;C
j
C
0
.j
2
C 1/:
Putting together these two lemmas, we see that when v satisfies (9.9),
(9.15) kv
k
2
L
2
.Q
j C1
/
0
.C
2
j
C 1/kvk
2
L
2
.Q
j
/
:
Now, if v satisfies (9.8), so does v
j
D v
j
,by(9.5). Note that v
j C1
D v
j
.From
here, the estimate on
(9.16) kvk
L
1
.
e
Q/
lim sup
j !1
kv
j
k
1=
j
L
2
.Q
j
/
goes precisely like the estimates on (9.16) in “14,” so we have the sup-norm
estimate:
Theorem 9.3. If v>0is a subsolution of @
t
L,then
(9.17) kvk
L
1
.
e
Q/
Kkvk
L
2
.Q/
;
where K D K.
0
;C
0
;n/.
Next we prepare to establish a Harnack inequality. Parallel to (9.24) of “14,”
we take w D
2
f
0
.u/ in (9.6), to get
(9.18)
“
2
f
00
.u/jr
x
uj
2
dt dV C
Z
2
f
u.T
2
;x/
dV
D2
“
h f
0
.u/r
x
u; r
x
i dt dV C 2
“
.@
t
/f .u/dtdV
C
Z
2
f
u.T
1
;x/
dV
if .@
t
L/u D 0 on ŒT
1
;T
2
,and .t; x/ D 0 for x near @.Ifwepickf.u/
to satisfy the differential inequality
(9.19) f
00
.u/ f
0
.u/
2
;
we have from (9.18)that
(9.20)
1
2
“
2
f
00
.u/jr
x
uj
2
dt dV C
Z
2
f
u.T
2
;x/
dV
2
“
jr
x
j
2
dt dV C 4
“
t
f.u/dt dV
C
Z
2
f
u.T
1
;x/
dV;
400 15. Nonlinear Parabolic Equations
provided .@
t
L/u D 0 on ŒT
1
;T
2
.Sincef
00
.u/jr
x
uj
2
f
0
.u/
2
jr
x
uj
2
D
jr
x
vj
2
,wehave
(9.21)
1
2
“
2
jr
x
vj
2
dt dV C
Z
2
v.T
2
;x/dV
2
“
jr
x
j
2
dt dV C 4
“
t
vdtdV C
Z
2
v.T
1
;x/dV:
If we take .t; x/ D '.x/ 2 C
1
0
./,wehave
(9.22)
1
2
“
'
2
jr
x
vj
2
dt dV C
Z
'
2
v.T
2
;x/dV
2.T
2
T
1
/
Z
jr
x
'j
2
dV C
Z
'
2
v.T
1
;x/dV:
We will apply the estimate (9.22) in the following situation. Suppose .@
t
L/u D 0 on Q D Œ0; T ; u 0 on ,and
(9.23) measf.t; x/ 2 Q W u.t; x/ 1g
1
2
meas Q:
Let be a ball in R
n
and O a concentric ball, such that
(9.24) meas O
3
4
meas :
Here, dV D bdxis used to compute the measure of a set in R
n
.Givenh>0,let
(9.25) O
t
.h/ Dfx 2 O W u.t; x/ hg;
t
.h/ Dfx 2 W u.t; x/ hg:
Pick ' 2 C
1
0
./ such that ' D 1 on O,andset
(9.26) v D f.u/ D log
C
1
u C h
:
Note that f satisfies the differential inequality (9.19), and f.u/ D 0 for u 1.
From the hypothesis (9.23), we can pick T
1
2 .0; T / such that
(9.27) meas
T
1
.1/
1
2
meas :
We let t be any point in .T
1
;Tand apply (9.22), with T
2
D t (discarding the first
integral). Since v log.1=2h/ for x 2 O n O
t
.h/ while v log.1=h/ on and
v D 0 on at least half of ,weget
(9.28)
log
1
2h
meas
O n O
t
.h/
K C
1
2
log
1
h
meas ;

9. Quasi-linear parabolic equations III (Nash–Moser estimates) 401
with K independent of h.Inviewof(9.24), this implies
(9.29) meas O
t
.h/
1
4
1
1 ı.h/
meas
K
.h/
;
where
.h/ D log
1
2h
;ı.h/D
log 2
log
1
h
:
Taking h sufficiently small, we have
Lemma 9.4. If u 0 on Q D Œ0; T satisfies .@
t
L/u D 0, then, under
the hypotheses (9.23) and (9.24), there exist h>0and T
1
<T such that, for all
t 2 .T
1
;T,
(9.30) meas
˚
x 2 O W u.t; x/ h
1
5
meas O:
We are now ready to prove the following Harnack-type inequality:
Proposition 9.5. Let u 0 be a solution to .@
t
L/u D 0 on Q D Œ0; T ,
where is a ball in R
n
centered at x
0
. Assume that (9.23) holds. Then there is
a concentric ball
e
, a number <T, and >0, depending only on Q and the
quantities
j
;b
j
in (9.2), such that
(9.31) u.t; x/ on Œ; T
e
D
e
Q:
Proof. Pick
0
2 .T
1
;T/,andletQ
0
D Œ
0
;T O. We will apply (9.22), with
the double integral taken over Q
0
, and with
(9.32) v D f.u/ D log
C
h
u C "
:
Here, h is as in (9.30), and we will take " 2 .0; h=2. With ' 2 C
1
0
.O/,(9.22)
yields
(9.33)
1
2
“
Q
0
'
2
jr
x
vj
2
dt dV K C
Z
O
'
2
v.
0
;x/dV K C C
1
log
h
"
:
Now v D f.u/ D 0 for u h, hence on the set O
t
.h/, whose measure was
estimated from below in (9.30). Thus, for each t 2 Œ
0
;T,
(9.34)
Z
e
O
v.t; x/
2
dV C
2
Z
e
O
ˇ
ˇ
r
x
v.t; x/
ˇ
ˇ
2
dV

402 15. Nonlinear Parabolic Equations
if we take
e
O to be a ball concentric with O, such that meas
e
O .9=10/ meas O.
We make ' D 1 on
e
O and conclude that
(9.35)
“
R
v
2
dt dV C
3
C C
4
log
h
"
; R D Œ
0
;T
e
O:
Since the function f in (9.32) is convex, we see that Theorem 9.3 applies to v.
Hence we obtain
e
Q R such that
(9.36) kvk
L
1
.
e
Q/
C kvk
L
2
.R/
C log
3h
"
:
Now, if we require that " 2 .0; h=2 and take " sufficiently small, this forces
(9.37) u "
1=2
" on
e
Q;
and the proposition is proved.
We now deduce the H¨older continuity of a solution to .@
t
L/u D 0 on
Q D Œ0; T from Proposition 9.5, by an argument parallel to that of (9.33)–
(9.39) of “14.” We have from (9.17) a bound ju.t; x/jK on any compact subset
e
Q of .0; T .Fix.t
0
;x
0
/ 2
e
Q,andlet
(9.38) !.r/ D sup
B
r
u.t; x/ inf
B
r
u.t; x/;
where
(9.39) B
r
D
˚
.t; x/ W 0 t
0
t ar
2
; jx x
0
jar
:
Say B
r
e
Q for r . Clearly, !./ 2K. Adding a constant to u, we can
assume
(9.40) sup
B
u.t; x/ Dinf
B
u.t; x/ D
1
2
!./ D M:
Then u
C
D 1 Cu=M and u
D 1u=M are annihilated by @
t
L. They are both
0 and at least one of them satisfies the hypotheses of Proposition 9.5 after we
rescale B
, dilating x by a factor of
1
and t by a factor of
2
. If, for example,
Proposition 9.5 applies to u
C
,wehaveu
C
.t; x/ in B
,forsome 2 .0; 1/.
Hence !./ .1 =2/!./. Iterating this argument, we obtain
(9.41) !.
/
1
2
!./;

9. Quasi-linear parabolic equations III (Nash–Moser estimates) 403
which implies H¨older continuity:
(9.42) !.r/ Cr
˛
;
for an appropriate ˛>0. We have proved the following:
Theorem 9.6. If u is a real-valued solution to (9.1)onI , with I D Œ0; T /,
then, given J D ŒT
0
;T/; T
0
2 .0; T /; O , we have for some >0an
estimate
(9.43) kuk
C
.J O/
C kuk
L
2
.I /
;
where C depends on the quantities
j
;b
j
in (9.2), but not on the modulus of
continuity of a
jk
.t; x/ or of b.t; x/.
Theorem 9.6 has the following implication:
Theorem 9.7. Let M be a compact, smooth manifold. Suppose u is a bounded,
real-valued function satisfying
(9.44)
@u
@t
D div
A.t; x/ grad u
on Œt
0
;t
0
C a M . Assume that A.t; x/ 2 End.T
x
M/satisfies
(9.45)
0
jj
2
˝
A.t; x/;
˛
1
jj
2
;
where the inner product and square norm are given by the metric tensor on M .
Then u.t
0
C a; x/ D w.x/ belongs to C
r
.M / for some r>0, and there is an
estimate
(9.46) kwk
C
r
K.M; a;
0
;
1
/ku.t
0
; /k
L
1
:
In particular, the factor K.M; a;
0
;
1
/ does not depend on the modulus of con-
tinuity of A.
We are now ready to establish some global existence results. For simplicity, we
take M D T
n
.
Proposition 9.8. Consider the equation
(9.47)
@u
@t
D
X
@
j
A
jk
.t; x; u/@
k
u; u.0/ D f:
Assume this is a scalar parabolic equation, so a
jk
D A
jk
.t; x; u/ satisfies (9.2),
with
j
D
j
.u/. Then the solution guaranteed by Proposition 8.4 exists for all
t>0.

404 15. Nonlinear Parabolic Equations
Proof. An L
1
-bound on u.t/ follows from the maximum principle, and then
(9.46)givesaC
r
-bound on u.t/,forsomer>0. Hence global existence follows
from Proposition 8.4.
Let us also consider the parabolic analogue of the PDE (10.1) of Chap. 14,
namely,
(9.48)
@u
@t
D
X
A
jk
.ru/@
j
@
k
u; u.0/ D f;
with
(9.49) A
jk
.p/ D F
p
j
p
k
.p/:
Again assume u is scalar. Also, for simplicity, we take M D T
n
.Wemakethe
hypothesis of uniform ellipticity:
(9.50) A
1
jj
2
X
F
p
j
p
k
.p/
j
k
A
2
jj
2
;
with 0<A
1
<A
2
< 1. Then Proposition 8.2 applies, given f 2 H
s
.M /,
s>n=2C 1.Furthermore,u
`
D @
`
u satisfies
(9.51)
@u
`
@t
D
X
@
j
A
jk
.ru/@
k
u
`
; u
`
.0/ D f
`
D @
`
f:
The maximum principle applies to both (9.48)and(9.51). Thus, given u 2
C.Œ0; T ; H
s
/ \ C
1
..0; T / M/,
(9.52) ju.t; x/jkf k
L
1
; ju
`
.t; x/jkf
`
k
L
1
;0 t<T:
Now the Nash–Moser theory applies to (9.51), to yield
(9.53) ku
`
.t; /k
C
r
.M /
K; 0 t<T;
for some r>0, as long as the ellipticity hypothesis (9.50) holds. Hence again we
can apply Proposition 8.4 to obtain global solvability:
Theorem 9.9. If F.p/ satisfies (9.50), then the scalar equation (9.48) has a so-
lution for all t>0, given f 2 H
s
.M /; s > n=2 C 1.
Parallel to the extension of estimates for solutions of Lu D 0 to the case
Lu D f made in Theorem 9.6 of Chap. 14, there is an extension of Theorem
9.6 of this chapter to the case
(9.54)
@u
@t
D Lu C f;
where L has the form (9.1).

9. Quasi-linear parabolic equations III (Nash–Moser estimates) 405
Theorem 9.10. Assume u is a real-valued solution to (9.54)onI , with
(9.55) sup
t2I
kf.t/k
L
p
.M /
K
0
;p>
n
2
:
Then u continues to satisfy an estimate of the form (9.43), with C also depending
on K
0
.
It is possible to modify the proof of Theorem 9.6 inChap.14toestablishthis.
Other approaches can be found in [LSU]and[Kry]. We omit details.
With this, we can extend the existence theory for (9.47) to scalar equations of
the form
(9.56)
@u
@t
D
X
@
j
A
jk
.t; x; u/@
k
u C '.u/; u.0/ D f:
An example is the equation
(9.57)
@u
@t
D
X
j
@
@x
j
u
@u
@x
j
C u.1 u/; u.0/ D f;
the multidimensional case of the equation (7.63) for a model of population growth.
We have the following result:
Proposition 9.11. Assume the equation (9.56) satisfies the parabolicity condition
(9.2), with
j
D
j
.u/. Suppose we have a
1
<a
2
in R, with '.a
1
/ 0; '.a
2
/
0.Iff 2 C
1
.M / takes values in the interval Œa
1
;a
2
,then(9.56) has a unique
solution u 2 C
1
Œ0; 1/ M
.
Proof. The local solution u 2 C
1
.Œ0; T / M/given by Proposition 8.3 has the
property that
(9.58) u.t; x/ 2 Œa
1
;a
2
; 8 t 2 Œ0; T /; x 2 M:
With this L
1
-bound, we deduce a C
r
-bound on u.t/, from Theorem 9.10,and
hence the continuation of u beyond t D T ,foranyT<1.
To see that (9.58) holds, we could apply a maximum-principle-type argument.
Alternatively, we can extend the Trotter product formula of 5 to treat time-
dependent operators, replacing L by L.t/. Then, for t 2 Œ0; T /,
(9.59) u.t/ D lim
n!1
S.t;t
n1
/F
t=n
S.t
1
;0/F
t=n
f;
where t
j
D .j=n/t; S.t; s/ is the solution operator to
(9.60)
@v
@t
D
X
@
j
A
jk
t;x;u.t; x/
@
k
v; S.t; s/v.s/ D v.t/;

406 15. Nonlinear Parabolic Equations
and F
t
is the flow on R generated by ', viewed as a vector field on R. In this case,
F
t=n
and S.t
j C1
;t
j
/ both preserve the class of smooth functions with values in
Œa
1
;a
2
.
We see that Proposition 9.11 applies to the population growth model (9.57)
whenever a
1
2 .0; 1 and a
2
2 Œ1; 1/.
We now mention some systems for which global existence can be proved via
Theorems 9.6–9.10. Keeping M D T
n
,letu D .u
1
;:::;u
`
/ take values in R
`
,
and consider
(9.61)
@u
@t
D
n
X
j D1
@
@x
j
D.u/
@u
@x
j
C X.u/; u.0/ D f;
where X is a vector field in R
`
and D.u/ is a diagonal ` ` matrix, with diagonal
entries d
k
2 C
1
.R
`
/ satisfying
(9.62) d
k
.u/>0; 8 u 2 R
`
:
We have the following; compare with Proposition 4.4.
Proposition 9.12. Assume there is a family of rectangles
(9.63) K
t
Dfv 2 R
`
W a
j
.t/ v
j
b
j
.t/; 1 j `g
such that
(9.64) F
t
X
.K
s
/ K
sCt
;s;t2 R
C
;
where F
t
X
is the flow on R
`
generated by X .Iff 2 C
1
.M / takes values in K
0
,
then, under the hypothesis (9.62) on the diagonal matrix D.u/, the system (9.61)
has a solution for all t 2 R
C
, and u.t; x/ 2 K
t
.
Proof. Using a product formula of the form (9.59), where S.t;s/ is the solution
operator to
(9.65)
@v
@t
D
n
X
j D1
@
@x
j
D.u/
@v
@x
j
; S.t; s/v.s/ D v.t/;
and F
t
D F
t
X
, we see that if u is a smooth solution to (9.61)fort 2 Œ0; T /,then
u.t; x/ 2 K
t
for all .t; x/ 2 Œ0; T / M , provided f.x/ 2 K
0
for all x 2 M .This
gives an L
1
-bound on u.t/.Now,for1 k `, regard each u
k
as a solution to
the nonhomogeneous scalar equation
(9.66)
@u
k
@t
D
X
j
@
@x
j
d
k
.u/
@u
k
@x
j
C F
k
;F
k
.t; x/ D X
k
u.t; x/
:

References 407
We can apply Theorem 9.10 to obtain H¨older estimates on each u
k
. Thus the
solution continues past t D T ,foranyT<1.
Exercises
1. Show that the scalar equation (9.56) has a solution for all t 2 Œ0; 1/ provided there
exist C;M 2 .0; 1/ such that
u M ) '.u/ C u; u M ) '.u/ C juj:
2. Formulate and establish generalizations to appropriate quasi-linear equations of results
in Exercises 2–6 of 4, on reaction-diffusion equations.
3. Reconsider (7.68), namely,
(9.67)
@u
@t
D .1 C u
2
x
/
1
u
xx
; u.0; x/ D f.x/:
Demonstrate global solvability, without the hypothesis jf
0
.x/jb<
p
1=3.More
generally, solve (7.65), under only the first of the two hypotheses in (7.66).
References
[Ar] D. Aronson, Density-dependent reaction-diffusion systems, pp. 161–176 in Dy-
namics and Modelling of Reaction Systems (W.Stout,W.Ray,andC.Conley,
eds.), Academic, New York, 1980.
[Ar2] D. Aronson, Regularity of flows in porus media, a survey, pp. 35–49 in
W.-M. Ni, L. Peletier, and J. Serrin (eds.), Nonlinear Diffusion Equations and
Their Equilibrium States, MSRI Publ., Vols. 12–13, Springer, New York, 1988.,
Part I.
[AS] D. Aronson and J. Serrin, Local behavior of solutions of quasilinear parabolic
equations, Arch. Rat. Mech. Anal. 25(1967), 81–122.
[AW1] D. Aronson and H. Weinberger, Nonlinear diffusion in population genet-
ics, combustion, and nerve propagation, pp. 5–49 in LNM #446, Springer,
New York, 1975.
[AW2] D. Aronson and H. Weinberger, Multidimensional nonlinear diffusion arising in
population genetics, Adv. Math. 30(1978), 37–76.
[BG] J. T. Beale and C. Greengard, Convergence of Euler–Stokes splitting of the
Navier–Stokes equations, Commun. Pure and Appl. Math. 47(1994), 1–27.
[Bram] M. Bramson, Convergence of travelling waves for systems of Kolmogorov-
like parabolic equations, pp. 179–190 in W.-M. Ni, L. Peletier, and J. Serrin
(eds.), Nonlinear Diffusion Equations and Their Equilibrium States,MSRI
Publ., Vols. 12–13, Springer, New York, 1988, Part I.
[BrP] H. Brezis and A. Pazy, Semigroups of nonlinear contractions on convex sets, J.
Funct. Anal. 6(1970), 237–281.
[Br] F. Browder, A priori estimates for elliptic and parabolic equations, Proc. Symp.
Pure Math. IV(1961), 73–81.
[CDH] J. Cannon, J. Douglas, and C. D. Hill, A multi-phase Stefan problem and the
disappearance of phases, J. Math. Mech. 17(1967), 21–34.
