Таранчук А.И. Адаптивные системы управления. Программа и методические указания к выполнению лабораторных работ
Подождите немного. Документ загружается.


11
где
12
11133
;baa34 5
2 113313313233
;baaaaaa1 22
3113323
.baaa1
С помощью (19) находятся корни характеристического полино%
ма
123
,,ррр, по знаку перед вещественной частью которых судят об
устойчивости системы.
Используя матрицы А и В, составим канонизирующую матрицу Р
1
.
С этой целью вычислим следующие определители:
12 1 2
12
11 12 13
2
12223123
31 32 33
0,
ba a
рpaacpcpc
bapa
3
45 3 3 5 6 6
33
(20)
где
12
111 23 33311 32
;; ;сb cba cb a33434
12
12
12
11 11 13
22345
31 31 33
00 ,
pa b a
pacpc
abpa
33
45 3 56
33
(21)
где
4315
; ...;cb c11
12
1
2
12
11 11
2
345
31 32 32
0
000 .
рa b
рpcpcp
aab
3
45 3 5 6
33
(22)
Тогда
321
154
54
0
0
ccc
pcc
cc
1
. (23)
Найдем обратную матрицу
1
1
Р
:
1
11
.РР Е1
(24)
Известно, что
1
,XPX1
11 1
11 1 1 1
,PPX PAPX PBU12
(25)
11
11 1
,XPAPXPBU12
.XAXBU12

12
Тогда можно определить каноническую форму для матриц А и В:
1
11
,АРАР1
(26)
1
1
.ВРВ1
(27)
Далее определяем матрицу коэффициентов обратной связи:
12
123
:,,,
Т
KKKK3 (28)
где
133
:,K 12 34
222
:,K 12 34
(29)
31 1
,K 12 34
где
1,2,3
1
–коэффициент желаемого характеристического многочле%
на;
1,2,3
1
–коэффициент характеристического многочлена из выраже%
ния (19).
Вычислив KР
1
–1
, получим выражение для вектора управления в
исходном базисе системы
1
1
.
T
UKPX1
(30)
2. Порядок выполнения работы
Модель системы без обратной связи приведена на рис. 9, а с обрат%
ной связью на рис. 10. Исходные данные для моделирования, в зави%
симости от варианта, приведены в табл. 4.
Таблица 4
атнаирав№
а–
11
–а
13
а–
23
а–
31
–а
32
а–
33
b
11
b
13
145,08,0010,00,101,101,001,05,0
265,09,0110,09,011,102,012,00,1
385,00,1210,08,021,103,003,05,1
406,05,1310,01,131,104,004,00,2
526,00,2410,
00,141,154,054,05,2
646,05,2510,051,151,105,005,00,3
766,00,3610,050,161,155,055,05,3
886,05,3710,02,171,106,006,00,4
907,00,4810,01,181,156
,056,05,4
0127,05,4910,052,191,107,007,00,5

13
Рис. 9
1
1
.
11
1
Step
Integrator
А31
А32
А33
В
31
В
21
А22
А23
А21
А11
А12
А13
В
11
Integrator1
Integrator2
S
1
S
1
S
14
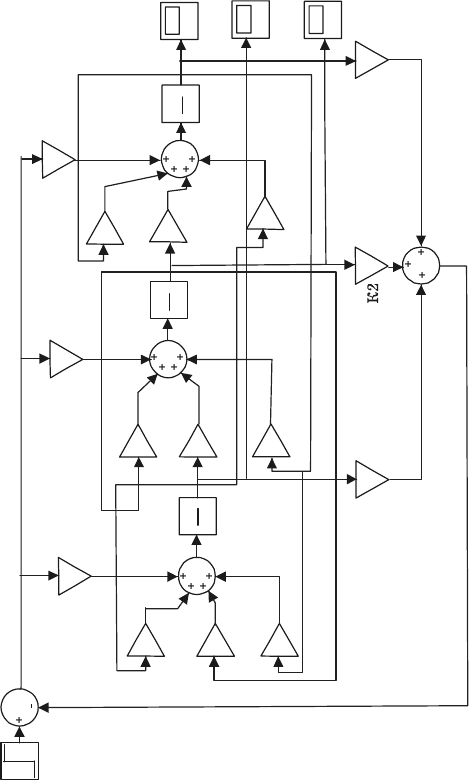
Рис. 10
Step
11
1
11
1
Integrator
А31
А32
А33
В
31
В
21
А22
А23
А21
А11
А12
А13
В
11
Х1
Х2
Х3
Integrator1
Integrator2
1
S
1
S
1
S
1
1
К1
К3
1
15
В соответствии с указанным преподавателем вариантом построим
две модели, приведенные на рис.9 и рис.10.
Используя пакет прикладных программ «Simulink» , наберем по%
лученные модели на ПЭВМ.
Процедура работы с пакетом приведена на с. 4 – 8 данных методи%
ческих указаний.
На экране монитора получаем три графика переходных процессов
компонент вектора состояния X
1
, X
2
, X
3
без обратной связи и три
графика с обратной связью.
3. Содержание отчета по лабораторной работе
Отчет должен содержать :
– уравнения модального регулятора;
– исходные данные для моделирования;
– исходные модели системы;
– графики переходных процессов;
– выводы по работе.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Катков М. С. Непрерывные системы адаптивного управления с
идентификаторами. М.: Мир книги, 1992. 385 с.
2. Справочник по теории автоматического управления/ Под ред.
А. А. Красовского. М.: Наука, 1987. 711 с.
3. Бесекерский В. А. , Попов Е. П. Теория систем автоматического
регулирования. М.: Наука, 1967. 767 с.
4. Соколов Н. И., Рутковский В. Ю., Судзиловский Н. Б. Адаптив%
ные системы автоматического управления летательными аппарата%
ми. М.: Машиностроение, 1978. 207 с.
16
Оглавление
Лабораторная работа № 1. Исследование беспоисковой
самонастраивающейся системы (БСС) с инверсной
эталонной моделью в обратной связи ....................... 1
Лабораторная работа №2. Исследование модального регулятора
при наличии полной информации о векторе состояния
в адаптивной системе ............................................ 9
Библиографический список ................................................ 15
