Tao R. Finite Automata and Application to Cryptography

Подождите немного. Документ загружается.

8.1 Canonical Form for Finite Automaton One Key Cryptosystems 275

...y

l+τ−1

= λ(s, x

...x

l+τ−1

...y

l+τ−1

is a ciphertext of x

...x

l−1

. For decryption, we compute



...x



l+τ−1

= λ



...y

l+τ−1

)

for any state s



of M



, then the plaintext x

...x

l−1

equals x



...x



l+τ−1

.In

this case, the key is the structure of M. In general, the variable structure

of the encoder leads its implementation to inconvenient. In the case where

M is weakly invertible with delay τ, we may choose its weak inverse ﬁnite

automaton with delay τ ,sayM



= Y,X, S



,δ



,λ



, as the corresponding

decoder. To encrypt a plaintext x

...x

l−1

in X

∗

, we ﬁrst expand randomly

τ letters x

,...,x

l+τ−1

in X to its end, then compute

...y

l+τ−1

= λ(s, x

...x

l+τ−1

...y

l+τ−1

is a ciphertext of x

...x

l−1

. For decryption, we compute



...x



l+τ−1

= λ



...y

l+τ−1

where the state s



of M



τ-matches s with delay τ . Then the plaintext

...x

l−1

equals x



...x



l+τ−1

. In this case, the key is the state s of M

if the structure of M is ﬁxed.

In invertible case, since M



is an input-memory ﬁnite automaton, an er-

ror letter in cipher causes at most τ + 1 error letters in decryption. But in

weakly invertible case, sometimes an error letter in cipher can cause inﬁnite

error letters in decryption as pointed out in p.35. From Theorem 1.5.2, to

guarantee bounded propagation of decoding errors, encoders must be feedfor-

ward invertible and their feedforward inverses are taken as the corresponding

decoders.

From Theorem 1.4.5, if M = X, Y, S, δ, λ is taken as an encoder, then

|Y |  |X|. To represent all ciphertexts for all plaintexts of length l (l log

|X|

bits), we need (l+τ )log

|Y | bits. Thus l log

|X|  (l+τ)log

|Y |. Therefore,

there is no plaintext expansion if and only if l log

|X| =(l + τ)log

|Y |,if

and only if |Y | = |X| and the delay step τ =0.

For one key cryptosystems implemented by ﬁnite automata without plain-

text expansion and with bounded propagation of decoding errors, decoders

may be chosen from weakly inverse semi-input-memory ﬁnite automata with

delay 0 in which the input alphabet and the output alphabet of a ﬁnite au-

tomaton have the same size. Theorem 5.2.2 characterizes the structure of

feedforward inverses with delay 0; using this result, we give a canonical form

of such cryptosystems as follows.

The decoder M



= Y, X, S



,δ



,λ



 is a c-order semi-input-memory ﬁnite

automaton SIM(M

,f), where X = Y , M

= Y

,δ

,λ

 is an au-

tonomous ﬁnite automaton, f is a single-valued mapping from Y

c+1

×λ

)

276 8. One Key Cryptosystems and Latin Arrays

to X with |f(Y, y

c−1

,...,y

,λ

))| = |X| for any s

∈ S

and any

,...,y

c−1

∈ Y . For any y

∈ λ

)andanyy

,...,y

c−1

∈ Y ,let

c−1

,...,y

be a single-valued mapping from Y to X deﬁned by

c−1

,...,y

)=f(y

,...,y

),y

∈ Y.

Clearly, f

c−1

,...,y

is a permutation on Y (or X). Then there exists a single-

valued mapping h from Y

× λ

)toW such that

f(y

c−1

,...,y

)=g

−1

h(y

c−1

,...,y

)

∈ λ

),y

,...,y

∈ Y

for some ﬁnite set W ,whereg

−1

is a bijection from Y to X, for any w in

W . Fig.8.1.1 (b) gives a pictorial form of the decoder M



. For any initial

state s



= y

−1

,...,y

−c

 and any input sequence (ciphertext) y

...y

l−1

of M



, the output sequence (plaintext) x

...x

l−1

of M



can be computed by

a,i+1

= δ

= λ

= h(y

i−1

,...,y

i−c

= g

−1

i =0, 1,...,l− 1.

Among others, a corresponding encoder may be chosen as a ﬁnite au-

tomaton M = X, Y , Y

× S

, δ, λ, of which a pictorial form is given by

Fig.8.1.1 (a), where

δ(y

−1

,...,y

−c

,x

)=y

−1

,...,y

−c+1

,δ

),

λ(y

−1

,...,y

−c

,x

)=y

= h(y

−1

,...,y

−c

,λ

)),

= g

y

−1

,...,y

−c

∈Y

× S

∈ X.

That is to say, for any initial state s

= y

−1

,...,y

−c

 and any in-

put sequence (plaintext) x

...x

l−1

of M , the output sequence (ciphertext)

...y

l−1

of M can be computed by

a,i+1

= δ

= λ

= h(y

i−1

,...,y

i−c

= g

i =0, 1,...,l− 1.

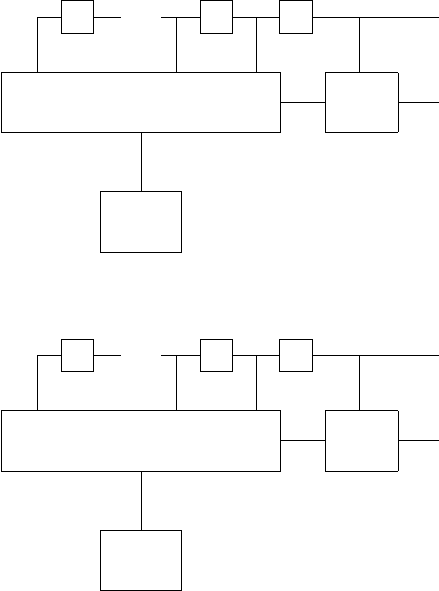
8.1 Canonical Form for Finite Automaton One Key Cryptosystems 277

h(y

i−1

,...,y

i−c

)

−1

)



···



i−c

i−2

i−1

(b) Decoder M



h(y

i−1

,...,y

i−c

)



···



 -

i−c

i−2

i−1

(a) Encoder M

Figure 8.1.1

Other decoders are possible; results in Sect. 6.6 of Chap. 6 show that, from

a behavior viewpoint, they are slightly diﬀerent from the above decoder.

On the other hand, other encoders are possible. We may even take nonde-

terministic encoders from results in Sect. 6.5 of Chap. 6. But they are more

complex than the above encoder from a structural viewpoint.

As a special case (c = 0), for one key cryptosystems implemented by

ﬁnite automata without expansion of the plaintext and without propagation

of decoding errors, the canonical form is as follows.

The decoder M



= Y,X,S

,δ



,λ



 is a 0-order semi-input-memory ﬁnite

automaton SIM(M



), where X = Y ,



,y)=δ



,y)=g

−1

(y),

w = λ

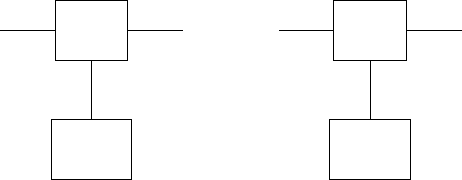
278 8. One Key Cryptosystems and Latin Arrays

∈ S

,y∈ Y,

= W, S

,δ

,λ

 is an autonomous ﬁnite automaton, g

−1

is a bijection

from Y to X for any w in W,andg

−1

(y)=g



(y, w). For any initial state s

and any input sequence (ciphertext) y

...y

l−1

of M



, the output sequence

(plaintext) x

...x

l−1

of M



can be computed by

a,i+1

= δ

= λ

= g

−1

i =0, 1,...,l− 1.

A corresponding encoder may be chosen as a ﬁnite automaton M = X,

Y , S

, δ, λ,whereX = Y ,

δ(s

,x)=δ

λ(s

,x)=g

(x),

w = λ

∈ S

,x∈ X.

That is to say, M = X, Y, S

,δ,λ is also a 0-order semi-input-memory

ﬁnite automaton SIM(M

,g), where g(x, w)=g

(x). For any initial state

and any input sequence (plaintext) x

...x

l−1

of M, the output sequence

(ciphertext) y

...y

l−1

of M can be computed by

a,i+1

= δ

= λ

= g

i =0, 1,...,l− 1.

Fig. 8.1.2 gives a pictorial form of the canonical form.

)

- -

(a) Encoder M

−1

)

- -

(b) Decoder M



Figure 8.1.2

8.2 Latin Arrays 279

Block ciphers and stream ciphers (in the narrow sense) are special cases

of the above canonical form. For block ciphers, δ

is the identity function.

For binary stream ciphers, g

(v)=g

−1

(v)=w ⊕ v.

Example 8.1.1. To give a cipher pictorialized by Fig. 8.1.1, let X and Y be

the set of all 8 bits 0,1 strings. Take c =6.M

consists of a binary shift

128

⊕ x

⊕ x and an autonomous

ﬁnite automaton M

of which the next state function is the identity function.

is s

,ϕ,wheres

is the state of the shift register and ϕ is the output

of M

which represents an involution (i.e., ϕ

−1

= ϕ) of 8 bits 0,1 strings.

is w

,ϕ,wherew

and w

are 8 bits 0,1 strings. g

w

,ϕ

(x)is

ϕ(w

− (w

⊕ (w

− ϕ(x)))), where − stands for subtraction modulo 256;

therefore, g

−1

w

,ϕ

(y)=g

w

,ϕ

(y). The key consists of the initial state

of M

If the characteristic polynomial of the binary shift register is variable

which may be taken as the product of x and any primitive polynomial of

degree 127 over GF (2), then the key consists of the initial state of M

and

the characteristic polynomial, in other words, the key consists of M

and its

initial state. Formally, the structure of M

is variable; but after redeﬁning

the autonomous ﬁnite automaton M

by expanding its state to include the

coeﬃcient of the characteristic polynomial, the key still consists of the initial

state of M

8.2 Latin Arrays

8.2.1 Deﬁnitions

The problem of designing one key cryptosystems implemented by ﬁnite au-

tomata without plaintext expansion and with bounded propagation of decod-

ing errors may be reduced to choosing suitable parameters such as the size

of alphabets and the length c of the ciphertext history and designing three

components in the above canonical form (Fig.8.1.1) – an autonomous ﬁnite

automaton M

, a transformation h and a permutational family {g

, w in W }

– so that the systems are both eﬃcient and secure.

Assume that the distribution of elements in the derived key sequence w

... in the above canonical form is uniform. Let {g

, w in W } be a family

of permutations on X. For resisting the known plaintext attack, under the

above assumption, the requirement in Property 1 is very natural.

Property 1. For any x, y in X, |{w|w in W, g

(x)=y}| = constant.

From the viewpoint of uniformity for permutations, the following property

is also desired.

280 8. One Key Cryptosystems and Latin Arrays

Property 2. For any w



in W , |{w|w in W, g

= g



}| = constant.

Specify an order for elements of X,sayx

, ..., x

, and an order for el-

ements of W ,sayw

, ..., w

.LetA be an n × m matrix, of which the

element at row i and column j is g

). Then each column of A is a per-

mutation of elements in X. Clearly, ﬁxing orders of elements for X and W ,

the family of permutations {g

, w in W } is one-to-one correspondent with

A. Corresponding to Property 1, we introduce the following concept.

Let A be an n × nk matrix over N = {1,...,n}. If each element of N

occurs exactly once in each column of A and k times in each row of A, A is

calledan(n, k)-Latin array.

Corresponding to Properties 1 and 2, we introduce the following concept.

Let A be an (n, k)-Latin array. If each column of A occurs exactly r times

in columns of A, A is called an (n, k, r)-Latin array.

Notice that (n, 1)-Latin arrays are n-order Latin squares in literature.

Let A and B be n × m matrices over N.IfB can be obtained from A by

rearranging rows, rearranging columns and renaming elements, we say that

A and B are isotopic; and the transformation α, β, γ is called an isotopism

from A to B,whereα, β and γ are the row arranging, the renaming and the

column arranging, respectively. It is easy to verify that the isotopy relation is

reﬂexive, symmetric and transitive. Clearly, if A

is an (n, k)-Latin array and

if A and B are isotopic, then B is an (n, k)-Latin array. Similarly, if A is an

(n, k, r)-Latin array and if A and B are isotopic, then B is an (n, k, r)-Latin

array.

For (n, k)-Latin arrays or (n, k, r)-Latin arrays, any equivalence class of

the isotopy relation is also called an isotopy class.

8.2.2 On (n, k, r)-Latin Arrays

We use U(n, k) to denote the number of all (n, k)-Latin arrays, U(n, k, r)

the number of all (n, k, r)-Latin arrays, I(n, k) the number of all isotopy

classes of (n, k)-Latin arrays, and I(n, k, r) the number of all isotopy classes

of (n, k, r)-Latin arrays.

Let A

be an n ×m

matrix, i =1,..., t.Then × (m

+ ···+ m

)matrix

, ..., A

] is called the concatenation of A

, ..., A

. The concatenation of t

identical matrices A is called the t-fold concatenation of A, denoted by A

(t)

It is easy to see that the concatenation [A

, ..., A

]ofthe(n, k

)-Latin

array A

, i =1,...,t is an (n, k

+ ···+ k

)-Latin array.

Let A and B be n × m matrices over N.IfB can be obtained from A by

rearranging A’s columns, we say that A and B are column-equivalent.

8.2 Latin Arrays 281

Clearly, the column-equivalence relation is reﬂexive, symmetric, and tran-

sitive. For (n, k)-Latin arrays or (n, k, r)-Latin arrays, the equivalence classes

of the column-equivalence relation are called the column-equivalence classes.

For any matrix A,weuseb(A) to denote the matrix obtained from A by

deleting repeated columns but the leftmost ones.

Lemma 8.2.1. (a) Let A be an (n, k, 1)-Latin array. Then A

(r)

is an

(n, k, r)-Latin array.

(b) Let A be an (n, k, r)-Latin array. Then r|k, b(A) is an (n, k/r, 1)-

Latin array, and A and the r-fold concatenation of b(A) are isotopic and

column-equivalent.

Proof. (a) From the deﬁnition, the result is evident.

(b) From the deﬁnitions, it is easy to see that A and b(A)

(r)

,ther-fold

concatenation of b(A), are column-equivalent; therefore, A and b(A)

(r)

are

isotopic. Let k



be the number of occurrences of an element y in row i of

b(A). Then the number of occurrences of the element y in row i of b(A)

(r)

is rk



.Sinceb(A)

(r)

and A are column-equivalent and A is an (n, k, r)-Latin

array, b(A)

(r)

is an (n, k, r)-Latin array. It follows that k = rk



.Thusr|k.

Since k



= k/r, k



is independent of y. Therefore, b(A)isan(n, k/r, 1)-Latin

array. 

Lemma 8.2.2. Let A and B be two (n, k, r)-Latin arrays.

(a) A and B are isotopic if and only if b(A) and b(B) are isotopic.

(b) A and B are column-equivalent if and only if b(A) and b(B) are

column-equivalent.

Proof. (a) Suppose that b(A)andb(B) are isotopic. It is easy to see that

b(A)

(r)

and b(B)

(r)

are isotopic. From Lemma 8.2.1(b), b(A)

(r)

and A are

isotopic, and b(B)

(r)

and B are isotopic. Therefore, A and B are isotopic.

Conversely, suppose that A and B are isotopic. Then there is an isotopism

α, β, γ from A to B.LetA



be the result obtained by applying row arrang-

ing α and renaming β to A.ThenB can be obtained by applying column

arranging γ from A



. Clearly, columns i and j of A are the same if and only

if columns i and j of A



are the same. This yields that if b(A) consists of

columns j

, ..., j

k/r

of A,thenb(A



) consists of columns j

, ..., j

k/r

of A



Thus applying row arranging α and renaming β to b(A) results b(A



). Since



and B are column-equivalent, it is easy to see that b(A



)andb(B)are

column-equivalent. It follows that b(A)andb(B) are isotopic.

(b) The proof of part (b) is similar to part (a). 

Theorem 8.2.1. (a) I(n, k, r)=I(n, k/r, 1).

(b) U (n, k, r)=U (n, k/r, 1)(nk)!/((nk/r)!(r!)

nk/r

282 8. One Key Cryptosystems and Latin Arrays

Proof. (a) We deﬁne a mapping ϕ from the isotopy classes of (n, k/r, 1)-

Latin arrays to the isotopy classes of (n, k, r)-Latin arrays by taking ϕ(C)

as the isotopy class containing A

(r)

,whereA is an arbitrary element in C.

From Lemma 8.2.1(a), A

(r)

is an (n, k, r)-Latin array. Noticing b(A

(r)

)=A

for any (n, k, 1)-Latin array A, from Lemma 8.2.2 (a), it is easy to show that

ϕ is single-valued and injective. From Lemma 8.2.1 (b), ϕ is surjective. Thus

we have I(n, k, r)=I(n, k/r, 1).

(b) Let C be an isotopy class of (n, k/r, 1)-Latin array, and C



= ϕ(C).

Since no column occurs repeatedly within any Latin array in C, each column-

equivalence class of C has (nk/r)! elements. Denote the number of column-

equivalence classes of C by x. Then the number of Latin arrays in C is

|C| =(nk/r)!x.

We deﬁne a mapping ψ from the column-equivalence classes of C to the

column-equivalence classes of C



by taking ψ(D) as the column-equivalence

class containing A

(r)

,whereA is an arbitrary element in D. From Lemma

8.2.2(b), it is easy to show that ψ is single-valued and injective. From

Lemma 8.2.1(b), ψ is surjective. Thus the number of column-equivalence

classes of C is equal to the number of column-equivalence classes of C



For any column-equivalence class D



of C



, it is easy to see that all el-

ements of D



can be obtained from an arbitrary speciﬁc element of D



rearranging columns. Since any Latin array in D



has nk columns and each

column occurs exactly r times, there are (nk)! ways to rearrange columns of

a speciﬁc Latin array of D



, and there are exactly (r!)

nk/r

ways generating

the same result. Therefore, the number of elements in D



is (nk)!/(r!)

nk/r

Using proven results, we conclude that the number of Latin arrays in C



| =((nk)!/(r!)

nk/r

=((nk)!/(r!)

nk/r

)|C|/(nk/r)!

= |C|(nk)!/((nk/r)!(r!)

nk/r

From (a), it follows that U(n, k, r)=U (n, k/r, 1)(nk)!/((nk/r)!(r!)

nk/r

). 

Let A be an (n, k, 1)-Latin array, and A



an (n, (n−1)!−k, 1)-Latin array.

If the columns of the concatenation of A and A



consist of all permutations

on N, A



is called a complement of A.

Clearly, if A



is a complement of A,thenA is a complement of A



.Any

two complements of A are column-equivalent.

Lemma 8.2.3. Let A

be an (n, k, 1)-Latin array, and A



a complement of

, i =1, 2.

(a) A

and A

are isotopic if and only if A



and A



are isotopic.

8.2 Latin Arrays 283

(b) A

and A

are column-equivalent if and only if A



and A



are column-

equivalent.

Proof. (a) Suppose that A

and A

are isotopic. Then there is an isotopism

from A

to A

,sayα, β, γ.Letγ



be a column arranging of n×(n!) matrices

so that the restriction of γ



on the ﬁrst nk columns is γ and γ



keeps the

last n! − nk columns unchanged. Let [A



] be the result of applying the

transformation α, β, γ



 to [A



]. Then we have A

= A

and that α, β, e

is an isotopism from A



to A



,wheree stands for the identical transformation.

Since the columns of [A



] consist of all permutations on N,thecolumns

of [A



] consist of all permutations on N.ThusA



is a complement of

. If follows that there exists a column arranging γ



from A



to A



.Thus

α, β, γ



 is an isotopism from A



to A



. Therefore, A



and A



are isotopic.

From symmetry, if A



and A



are isotopic, then A

and A

are isotopic.

(b) From the proof of (a), taking α and β as the identity transformation

results a proof of (b). 

Theorem 8.2.2. Let 1  k<(n − 1)!.

(a) I(n, k, 1) = I(n, (n − 1)! − k, 1).

(b) U (n, (n − 1)! − k, 1) = U(n, k, 1)(n! − nk)!/(nk)!.

Proof. (a) We deﬁne a mapping ϕ from the isotopy classes of (n, k, 1)-Latin

arrays to the isotopy classes of (n, (n−1)! −k, 1)-Latin arrays so that ϕ maps

the isotopy class containing A

to the isotopy class containing a complement of

A. From Lemma 8.2.3(a), ϕ is single-valued and injective. Since complements

of any (n, (n − 1)! − k, 1)-Latin array are existent, ϕ is surjective. Therefore,

we have I(n, k, 1) = I(n, (n − 1)! − k, 1).

(b) For any isotopy class of (n, k, 1)-Latin arrays C,letC



= ϕ(C).

Clearly, the number of elements of any column-equivalence class of C is (nk)!.

Denote the number of column-equivalence classes of C by x. Then the number

of Latin arrays in C is |C| =(nk)!x.

We deﬁne a mapping ψ from the column-equivalence classes of C to the

column-equivalence classes of C



so that ψ maps the column-equivalence class

containing A to the column-equivalence class containing a complement of

A. From Lemma 8.2.3(b), ψ is single-valued and injective. Since for each

(n, (n − k)! − k, 1)-Latin array in C



thereisan(n, k, 1)-Latin array in C as

its complement, ψ is surjective. Therefore, the number of column-equivalence

classes of C is equal to the number of column-equivalence classes of C



Clearly, the number of elements of any column-equivalence class of C



(n!−nk)!. It follows that the number of Latin arrays in C



is |C



| =(n!−nk)!x.

284 8. One Key Cryptosystems and Latin Arrays

Using proven results, we conclude that the number of Latin arrays in C



is |C



| =(n! − nk)!x =(n! − nk)!(|C|/(nk)!) = |C|(n! − nk)!/(nk)!. From (a),

it follows that U(n, (n − 1)! − k, 1) = U(n, k, 1)(n! − nk)!/(nk)!.

8.2.3 Invariant

Let A be an (n, k)-Latin array.

For any column in a matrix, the multiplicity of the column means the oc-

currence number of the column in the matrix. We use c

to denote the number

of distinct columns of A with multiplicity i,fori =1,...,k. c

k−1

...c

called the column characteristic value of A.

For any sequence (x

,...,x

), x

taking value from an arbitrary set with

n − 1elements,n

k−1

...n

is called the type of the sequence, where n

the number of distinct x

’s with multiplicity j. In the case of k = 2, possible

types are 1 and 0 which are referred to as twins and all diﬀerent, respectively.

Inthecaseofk = 3, possible types are 10, 01 and 00 which are referred to as

trio, twins and all diﬀerent, respectively. In the case of k = 4, possible types

are 100, 010, 002 and 001 which are referred to as quad, trio, double twins

and twins, respectively.

For any diﬀerent i and j,weuseA(i, j, a)todenotethej-th row of the

submatrix consisting of A’s columns of which the elements at row i are a.

Let c

be the number of a,1 a  n, such that the type of A(i, j, a)ist;

denote T

(i, j)=



t · c

, t ranging over all types. Noting



= n,any

can be determined by other c

’s. Fixing a permutation of all types, say

,...,t

, T

(i, j) is also represented by c

r−1

...c

. For example, in the

case of (4, 2)-Latin array, we permute types as 1, 0 and represent T

(i, j)by

; in the case of (4, 3)-Latin array, we permute types as 10, 01, 00 and rep-

resent T

(i, j)byc

; in the case of (4, 4)-Latin array, we permute types

as 100, 010, 002, 001 and represent T

(i, j)byc

100

010

002

.Givendiﬀerenti

and j, i = j, for any a, 1  a  n,ifinthetypen

k−1

...n

of A(i, j, a)the

nonzero n

with the maximal subscript h takes value 1, then we deﬁne π(a)

as the element in A(i, j, a) with the maximal multiplicity. If the mapping π

is bijective, π is called the derived permutation from row i to row j, denoted

by π(i, j). A derived permutation can be expressed as a product of disjoint

cycles of length > 1. The distribution of these lengths of cycles is called the

type of the derived permutation, denoted by T

(i, j). If the derived permuta-

tion does not exist and if the maximal multiplicity of elements occurring in

A(i, j, 1),...,A(i, j, n), say r, is great than k/2, |I ∩ J| is called the intersec-

tion number from row i to row j, denoted by T

(i, j), where I = {a | a ∈ N,

the maximal multiplicity of elements in A(i, j, a)isr},andJ = {b | there