Tan S.T. Finite Mathematics for the Managerial, Life, and Social Sciences

Подождите немного. Документ загружается.

482 8 PROBABILITY DISTRIBUTIONS AND STATISTICS

3. Find the mean, variance, and standard deviation of a ran-

dom variable X having the following probability distribu-

tion:

x 3 10 1 3 5

P(X  x) .08 .24 .32 .16 .12 .08

4. A binomial experiment consists of four independent trials,

and the probability of success in each trial is 0.3.

a. Find the probability of obtaining 0, 1, 2, 3, and 4 suc-

cesses, respectively.

b. Compute the mean and standard deviation of the ran-

dom variable associated with this experiment.

5. Let X be a normal random variable with ␮  60 and

␴  5. Find the values of (a) P(X  70), (b) P(X  50),

and (c) P(50  X  70).

6. A fair coin is tossed 30 times. Using the appropriate nor-

mal distribution to approximate a binomial distribution,

find the probability of obtaining (a) fewer than 10 heads,

(b) between 12 and 16 heads, inclusive, and (c) more than

20 heads.

87533_08_ch8_p417-482 1/30/08 10:10 AM Page 482

After the successful implementation

of an urban renewal program, what

percentage of the population of a

metropolitan area will live in the city,

and what percentage of the

population will live in the suburbs?

In Examples 4 and 5, pages

487–488, we show how we can find

the population distribution over the

next few years for a population that

can be described by a Markov

process.

N THIS CHAPTER, we look at two important applications of

mathematics that are based primarily on matrix theory and the

theory of probability. Both of these applications, Markov chains

and the theory of games, are relatively recent developments in

the field of mathematics and have wide applications in many

practical areas.

MARKOV CHAINS

AND THE THEORY

OF GAMES

87533_09_ch9_p483-536 1/30/08 10:12 AM Page 483

484 9 MARKOV CHAINS AND THE THEORY OF GAMES

Transitional Probabilities

A finite stochastic process, you may recall, is an experiment consisting of a finite num-

ber of stages in which the outcomes and associated probabilities at each stage depend on

the outcomes and associated probabilities of the preceding stages. In this chapter, we are

concerned with a special class of stochastic processes—namely, those in which the prob-

abilities associated with the outcomes at any stage of the experiment depend only on the

outcomes of the preceding stage. Such a process is called a Markov process, or a

Markov chain, named after the Russian mathematician A. A. Markov (1856–1922).

The outcome at any stage of the experiment in a Markov process is called the

state of the experiment. In particular, the outcome at the current stage of the experi-

ment is called the current state of the process. Here is a typical problem involving a

Markov chain:

Starting from one state of a process (the current state), determine the probability that

the process will be at a particular state at some future time.

APPLIED EXAMPLE 1

Common Stocks An analyst at Weaver and

Kline, a stock brokerage firm, observes that the closing price of the pre-

ferred stock of an airline company over a short span of time depends only on its

previous closing price. At the end of each trading day, he makes a note of the

stock’s performance for that day, recording the closing price as “higher,”

“unchanged,” or “lower” according to whether the stock closes higher, un-

changed, or lower than the previous day’s closing price. This sequence of obser-

vations may be viewed as a Markov chain.

The transition from one state to another in a Markov chain may be studied with

the aid of tree diagrams, as in the next example.

APPLIED EXAMPLE 2

Common Stocks Refer to Example 1. If on a

certain day the stock’s closing price is higher than that of the previous day,

then the probability that it closes higher, unchanged, or lower on the next trading

day is .2, .3, and .5, respectively. Next, if the stock’s closing price is unchanged

from the previous day, then the probability that it closes higher, unchanged, or

lower on the next trading day is .5, .2, and .3, respectively. Finally, if the stock’s

closing price is lower than that of the previous day, then the probability that it

closes higher, unchanged, or lower on the next trading day is .4, .4, and .2, re-

spectively. With the aid of tree diagrams, describe the transition between states

and the probabilities associated with these transitions.

Solution

The Markov chain being described has three states: higher, un-

changed, and lower. If the current state is higher, then the transition to the other

states from this state may be displayed by constructing a tree diagram in which the

associated probabilities are shown on the appropriate limbs (Figure 1). Tree dia-

Higher

Unchanged

Lower

Unchanged

Higher

Unchanged

Lower

Higher

Unchanged

Lower

FIGURE 1

Tree diagrams showing transition probabilities between states

9.1 Markov Chains

87533_09_ch9_p483-536 1/30/08 10:12 AM Page 484

grams describing the transition from each of the other two possible current states,

unchanged and lower, to the other states are constructed in a similar manner.

The probabilities encountered in this example are called transition probabilities

because they are associated with the transition from one state to the next in the Markov

process. These transition probabilities may be conveniently represented in the form

of a matrix. Suppose for simplicity that we have a Markov chain with three possible

outcomes at each stage of the experiment. Let’s refer to these outcomes as state 1,

state 2, and state 3. Then the transition probabilities associated with the transition from

state 1 to each of the states 1, 2, and 3 in the next phase of the experiment are precisely

the respective conditional probabilities that the outcome is state 1, state 2, and state 3

given that the outcome state 1 has occurred. In short, the desired transition probabili-

ties are P(state 1 兩 state 1), P(state 2 兩 state 1), and P(state 3 兩 state 1), respectively.

Thus, we write

Next state

 P(state 1 兩 state 1)

 P(state 2 兩 state 1)

 P(state 3 兩 state 1)

Current state

Note that the first subscript in this notation refers to the state in the next stage of the

experiment, and the second subscript refers to the current state. Using a tree diagram,

we have the following representation:

Similarly, the transition probabilities associated with the transition from state 2 and

state 3 to each of the states 1, 2, and 3 are

 P(state 1 兩 state 2) and a

 P(state 1 兩 state 3)

 P(state 2 兩 state 2) a

 P(state 2 兩 state 3)

 P(state 3 兩 state 2) a

 P(state 3 兩 state 3)

These observations lead to the following matrix representation of the transition

probabilities:

Current state

State 1 State 2 State 3

State 1

Next state State 2

State 3

EXAMPLE 3

Use a matrix to represent the transition probabilities obtained in

Example 2.

Solution

There are three states at each stage of the Markov chain under considera-

tion. Letting state 1, state 2, and state 3 denote the states “higher,” “unchanged,”

and “lower,” respectively, we find that

 .2 a

 .3 a

 .5

State 1

State 2

State 3

9.1 MARKOV CHAINS 485

—

씮

—

씮

—

씮

—————

씮

87533_09_ch9_p483-536 1/30/08 10:12 AM Page 485

and so on, so the required matrix representation is given by

T 

The matrix obtained in Example 3 is a transition matrix. In the general case, we

have the following definition:

Since a

 P(state i 兩 state j) is the probability of the occurrence of an event, it must

be nonnegative, and this is precisely what Property 1 implies. Property 2 follows from

the fact that the transition from any one of the current states must terminate in one of

the n states in the next stage of the experiment. Any square matrix satisfying proper-

ties 1 and 2 is referred to as a stochastic matrix.

One advantage in representing the transition probabilities in the form of a matrix

is that we may use the results from matrix theory to help us solve problems involving

Markov processes, as we will see in the next several sections.

Next, for simplicity, let’s consider the following Markov process where each

stage of the experiment has precisely two possible states.

Transition Matrix

A transition matrix associated with a Markov chain with n states is an n  n

matrix T with entries a

(1  i  n, 1  j  n)

having the following properties:

1. a

 0 for all i and j.

2. The sum of the entries in each column of T is 1.

.2 .5 .4

.3 .2 .4

.5 .3 .2

486 9 MARKOV CHAINS AND THE THEORY OF GAMES

Current state

State 1 State 2

. . .

State j

. . .

State n

State 1 a

. . .

State 2 a

. . .

. .. . .

T 

State i a

. . .

. .. . .

State n a

. . .

state

Explore & Discuss

Let

A  and B 

be two 2  2 stochastic matrices, where 0  p  1, 0  q  1, 0  r  1, and

0  s  1.

1. Show that AB is a 2  2 stochastic matrix.

2. Use the result of part (a) to explain why A

, A

, . . . , A

, where n is a positive integer,

are also 2  2 stochastic matrices.

1  r 1  s

1  p 1  q

87533_09_ch9_p483-536 1/30/08 10:12 AM Page 486

APPLIED EXAMPLE 4

Urban–Suburban Population Flow Because

of the continued successful implementation of an urban renewal program, it

is expected that each year 3% of the population currently residing in the city will

move to the suburbs and 6% of the population currently residing in the suburbs

will move into the city. At present, 65% of the total population of the metropoli-

tan area lives in the city itself, while the remaining 35% lives in the suburbs.

Assuming that the total population of the metropolitan area remains constant,

what will be the distribution of the population 1 year from now?

Solution

This problem may be solved with the aid of a tree diagram and the

techniques of Chapter 7. The required tree diagram describing this process is

shown in Figure 2. Using the method of Section 7.5, we find that the probabil-

ity that a person selected at random will be a city dweller 1 year from now is

given by

(.65)(.97)  (.35)(.06)  .6515

In a similar manner, we find that the probability that a person selected at random

will reside in the suburbs 1 year from now is given by

(.65)(.03)  (.35)(.94)  .3485

Thus, the population of the area 1 year from now may be expected to be distrib-

uted as follows: 65.15% living in the city and 34.85% residing in the suburbs.

Let’s reexamine the solution to this problem. As noted earlier, the process under

consideration may be viewed as a Markov chain with two possible states at each stage

of the experiment: “living in the city” (state 1) and “living in the suburbs” (state 2).

The transition matrix associated with this Markov chain is

State 1 State 2

T  Transition matrix

Next, observe that the initial (current) probability distribution of the population may

be summarized in the form of a column vector of dimension 2 (that is, a 2  1 matrix).

Thus,

 Initial-state matrix

Using the results of Example 4, we may write the population distribution 1 year later

 Distribution after 1 year

.6515

.3485

State 1

State 2

.65

.35

State 1

State 2

.97 .06

.03 .94

State 1

State 2

City

.65

.35

City

.97

.03

City

.06

.94

Current

population

Population

one year later

Suburbs

9.1 MARKOV CHAINS 487

FIGURE 2

Tree diagram showing a Markov process

with two states: living in the city and liv-

ing in the suburbs

87533_09_ch9_p483-536 1/30/08 10:12 AM Page 487

You may now verify that

so this problem may be solved using matrix multiplication.

APPLIED EXAMPLE 5

Urban–Suburban Population Flow Refer to

Example 4. What is the population distribution of the city after 2 years?

After 3 years?

Solution

Let X

be the column vector representing the population distribu-

tion of the metropolitan area after 2 years. We may view X

, the vector

representing the population distribution of the metropolitan area after 1 year,

as representing the “initial” probability distribution in this part of our calcula-

tion. Thus,

The vector representing the probability distribution of the metropolitan area after

3 years is given by

That is, after 3 years, the population will be distributed as follows: 65.41% will

live in the city, and 34.59% will live in the suburbs.

Distribution Vectors

Observe that, in the foregoing computations, we have X

 TX

, X

 TX

 T

and X

 TX

 T

. These results are easily generalized. To see this, suppose

we have a Markov process in which there are n possible states at each stage of

the experiment. Suppose further that the probability of the system being in state 1,

state 2, . . . , state n, initially, is given by p

, p

, . . . , p

, respectively. This distri-

bution may be represented as an n-dimensional vector



冤



冥



called a distribution vector. If T represents the n  n transition matrix associated

with the Markov process, then the probability distribution of the system after m obser-

vations is given by

 T

(1)

APPLIED EXAMPLE 6

Taxicab Movement To keep track of the loca-

tion of its cabs, Zephyr Cab has divided a town into three zones: zone I,

zone II, and zone III. Zephyr’s management has determined from company

records that of the passengers picked up in zone I, 60% are discharged in the

 TX

⬇ c

.97 .06

.03 .94

d c

.6529

.3471

d⬇ c

.6541

.3459

 TX

 c

.97 .06

.03 .94

d c

.6515

.3485

d⬇ c

.6529

.3471

 c

.97 .06

.03 .94

d c

.65

.35

d c

.6515

.3485

d X

488 9 MARKOV CHAINS AND THE THEORY OF GAMES

87533_09_ch9_p483-536 1/30/08 10:12 AM Page 488

same zone, 30% are discharged in zone II, and 10% are discharged in zone III.

Of those picked up in zone II, 40% are discharged in zone I, 30% are discharged

in zone II, and 30% are discharged in zone III. Of those picked up in zone III,

30% are discharged in zone I, 30% are discharged in zone II, and 40% are dis-

charged in zone III. At the beginning of the day, 80% of the cabs are in zone I,

15% are in zone II, 5% are in zone III. Furthermore, a taxi without a passenger

will cruise within the zone it is currently in until a pickup is made.

a. Find the transition matrix for the Markov chain that describes the successive

locations of a cab.

b. What is the distribution of the cabs after all of them have made one pickup

and discharge?

c. What is the distribution of the cabs after all of them have made two pickups

and discharges?

Solution

Let zone I, zone II, and zone III correspond to state 1, state 2, and state 3

of the Markov chain.

a. The required transition matrix is given by

b. The initial distribution vector associated with the problem is

If X

denotes the distribution vector after one observation—that is, after all the

cabs have made one pickup and discharge—then

That is, 55.5% of the cabs are in zone I, 30% are in zone II, and 14.5% are in

zone III.

c. Let X

denote the distribution vector after all the cabs have made two pickups

and discharges. Then

That is, 49.65% of the cabs are in zone I, 30% are in zone II, and 20.35% are

in zone III. You should verify that the same result may be obtained by com-

puting T

Note

In this simplified model, we do not take into consideration variable demand

and variable delivery time.

 £

.6 .4 .3

.3 .3 .3

.1 .3 .4

§ £

.555

.300

.145

§ £

.4965

.3000

.2035

 TX

 £

.6 .4 .3

.3 .3 .3

.1 .3 .4

§ £

.80

.15

.05

§ £

.555

.300

.145

 TX

 £

.80

.15

.05

T  £

.6 .4 .3

.3 .3 .3

.1 .3 .4

9.1 MARKOV CHAINS 489

87533_09_ch9_p483-536 1/30/08 10:12 AM Page 489

490 9 MARKOV CHAINS AND THE THEORY OF GAMES

1. What is a finite stochastic process? What can you say about

the finite stochastic processes in a Markov chain?

2. Define the following terms for a Markov chain:

a. State

b. Current state

c. Transition probabilities

3. Consider a transition matrix T for a Markov chain with

entries a

, where 1  i  n and 1  j  n.

a. If there are n states associated with the Markov chain,

what is the size of the matrix T ?

b. Describe the probability that each entry represents. Can

an entry be negative?

c. What is the sum of the entries in each column of T ?

In Exercises 1–10, determine which of the matrices are

stochastic.

1. 2.

3. 4.

5. 6.

7. 8.

9. 10. ≥

.5 .2 .3

.2 .3 .2

.3 .4 .1

0.1.4

¥£

.2 .3

.3 .1

.5 .6

100

001

010

§£

.1 .4 .3

.7 .2 .1

.2 .4 .6

0 

§£

.3 .2 .4

.4 .7 .3

.3 .1 .2

§c

.8 .2

.3 .7

.4 .7

.6 .3

11. The transition matrix for a Markov process is given by

State

T 

State

State 2

a. What does the entry a

 .3 represent?

b. Given that the outcome state 1 has occurred, what is the

probability that the next outcome of the experiment will

be state 2?

c. If the initial-state distribution vector is given by



State 1

State 2

find TX

, the probability distribution of the system after

one observation.

12. The transition matrix for a Markov process is given by

State

T 

State 1

State 2

a. What does the entry a





represent?

b. Given that the outcome state 1 has occurred, what is the

probability that the next outcome of the experiment will

be state 2?

.3 .6

.7 .4

9.1 Self-Check Exercises

1. Three supermarkets serve a certain section of a city. Dur-

ing the upcoming year, supermarket A is expected to retain

80% of its customers, lose 5% of its customers to super-

market B, and lose 15% to supermarket C. Supermarket B

is expected to retain 90% of its customers and lose 5% of

its customers to each of supermarkets A and C. Supermar-

ket C is expected to retain 75% of its customers, lose 10%

to supermarket A, and lose 15% to supermarket B. Con-

struct the transition matrix for the Markov chain that

describes the change in the market share of the three super-

markets.

2. Refer to Self-Check Exercise 1. Currently the market

shares of supermarket A, supermarket B, and supermarket

C are 0.4, 0.3, and 0.3, respectively.

a. Find the initial distribution vector for this Markov

chain.

b. What share of the market will be held by each super-

market after 1 yr? Assuming that the trend continues,

what will be the market share after 2 yr?

Solutions to Self-Check Exercises 9.1 can be found on

page 493.

9.1 Exercises

9.1 Concept Questions

87533_09_ch9_p483-536 1/30/08 10:12 AM Page 490

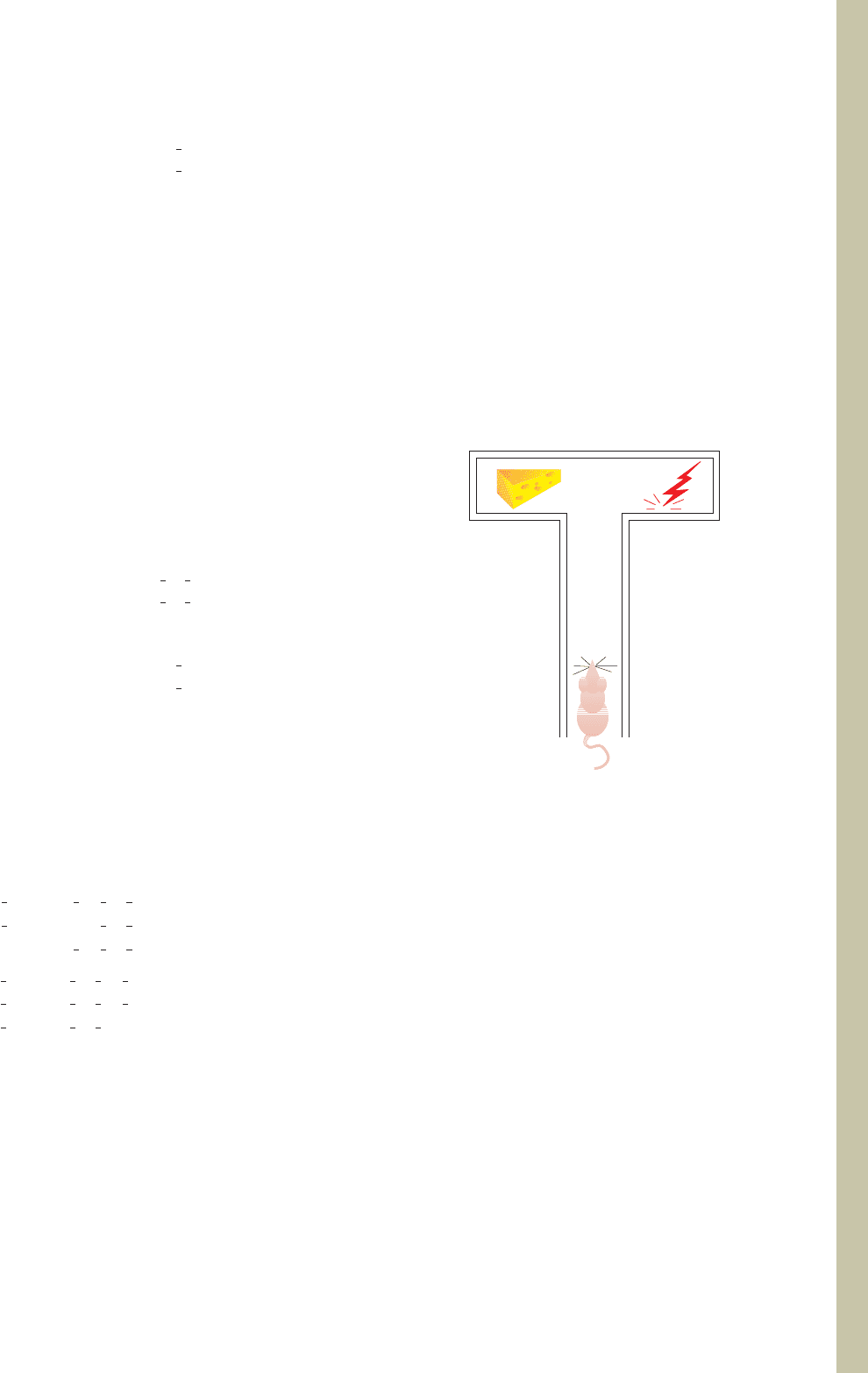
c. If the initial-state distribution vector is given by



State 1

State 2

find TX

, the probability distribution of the system after

one observation.

13. The transition matrix for a Markov process is given by

State

T 

State 1

State 2

and the initial-state distribution vector is given by



State 1

State 2

Find TX

and interpret your result with the aid of a tree dia-

gram.

14. The transition matrix for a Markov process is given by

State

T 

State 1

State 2

and the initial-state distribution vector is given by



State 1

State 2

Find TX

and interpret your result with the aid of a tree dia-

gram.

In Exercises 15–18, find X

(the probability distribution of

the system after two observations) for the distribution

vector X

and the transition matrix T.

15. X

 , T 

16. X

 , T 

17. X

 , T 

18. X

 , T 

19. P

SYCHOLOGY

XPERIMENTS

A psychologist conducts an

experiment in which a mouse is placed in a

T-maze, where

it has a choice at the

T-junction of turning left and receiv-

ing a reward (cheese) or turning right and receiving a mild

electric shock (see accompanying figure). At the end of

each trial, a record is kept of the mouse’s response. It is

observed that the mouse is as likely to turn left (state 1) as

.1 .1 .3

.8 .7 .2

.1 .2 .5

§£

.25

.40

.35

§£

.4 .8

.6 .2

.4 .8

right (state 2) during the first trial. In subsequent trials,

however, the observation is made that if the mouse had

turned left in the previous trial, then on the next trial the

probability that it will turn left is .8, whereas the probabil-

ity that it will turn right is .2. If the mouse had turned right

in the previous trial, then the probability that it will turn

right on the next trial is .1, whereas the probability that it

will turn left is .9.

a. Using a tree diagram, describe the transitions between

states and the probabilities associated with these transi-

tions.

b. Represent the transition probabilities obtained in part

(a) in terms of a matrix.

c. What is the initial-state probability vector?

d. Use the results of parts (b) and (c) to find the probabil-

ity that a mouse will turn left on the second trial.

20. S

MALL

-T

OWN

EVIVAL

At the beginning of 1998, the popu-

lation of a certain state was 55.4% rural and 44.6% urban.

Based on past trends, it is expected that 10% of the popu-

lation currently residing in the rural areas will move into

the urban areas, while 17% of the population currently

residing in the urban areas will move into the rural areas in

the next decade. What was the population distribution in

that state at the beginning of 2008?

21. P

OLITICAL

OLLS

Morris Polling conducted a poll 6 mo

before an election in a state in which a Democrat and a

Republican were running for governor and found that 60%

of the voters intended to vote for the Republican and 40%

intended to vote for the Democrat. In a poll conducted

3 mo later, it was found that 70% of those who had earlier

stated a preference for the Republican candidate still main-

tained that preference, whereas 30% of these voters now

preferred the Democratic candidate. Of those who had ear-

lier stated a preference for the Democrat, 80% still main-

tained that preference, whereas 20% now preferred the

Republican candidate.

a. If the election were held at this time, who would win?

b. Assuming that this trend continues, which candidate is

expected to win the election?

Cheese

Mild shock

9.1 MARKOV CHAINS 491

87533_09_ch9_p483-536 1/30/08 10:12 AM Page 491