Tan S.T. Finite Mathematics for the Managerial, Life, and Social Sciences
Подождите немного. Документ загружается.

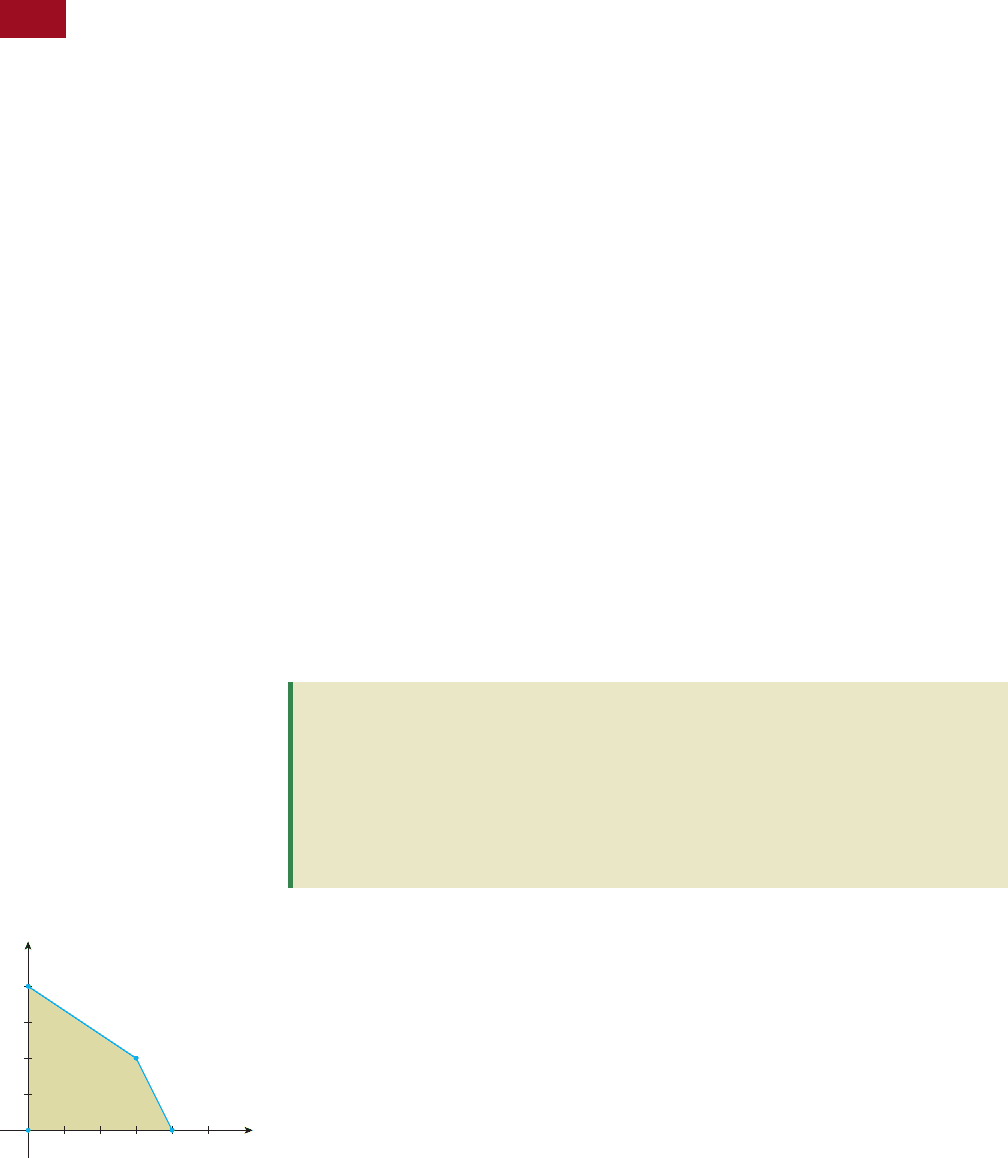
202 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
The Simplex Method
As mentioned in Chapter 3, the method of corners is not suitable for solving linear
programming problems when the number of variables or constraints is large. Its major
shortcoming is that a knowledge of all the corner points of the feasible set S associ-
ated with the problem is required. What we need is a method of solution that is based
on a judicious selection of the corner points of the feasible set S, thereby reducing the
number of points to be inspected. One such technique, called the simplex method, was
developed in the late 1940s by George Dantzig and is based on the Gauss–Jordan
elimination method. The simplex method is readily adaptable to the computer, which
makes it ideally suitable for solving linear programming problems involving large
numbers of variables and constraints.
Basically, the simplex method is an iterative procedure; that is, it is repeated over
and over again. Beginning at some initial feasible solution (a corner point of the fea-
sible set S, usually the origin), each iteration brings us to another corner point of S,
usually with an improved (but certainly no worse) value of the objective function. The
iteration is terminated when the optimal solution is reached (if it exists).
In this section, we describe the simplex method for solving a large class of prob-
lems that are referred to as standard maximization problems.
Before stating a formal procedure for solving standard linear programming prob-
lems based on the simplex method, let’s consider the following analysis of a two-
variable problem. The ensuing discussion will clarify the general procedure and at the
same time enhance our understanding of the simplex method by examining the moti-
vation that led to the steps of the procedure.
Consider the linear programming problem presented at the beginning of Section 3.3:
Maximize (1)
subject to
(2)
You can easily verify that this is a standard maximization problem. The feasible
set S associated with this problem is reproduced in Figure 1, where we have labeled
the four feasible corner points A(0, 0), B(4, 0), C(3, 2), and D(0, 4). Recall that the
optimal solution to the problem occurs at the corner point C(3, 2).
To solve this problem using the simplex method, we first replace the system of
inequality constraints (2) with a system of equality constraints. This may be accom-
plished by using nonnegative variables called slack variables. Let’s begin by consid-
ering the inequality
2x 3y 12
x 0, y 0
2x y 8
2x 3y 12
P 3x 2y
A Standard Linear Programming Problem
A standard maximization problem is one in which
1. The objective function is to be maximized.
2. All the variables involved in the problem are nonnegative.
3. All other linear constraints may be written so that the expression involving
the variables is less than or equal to a nonnegative constant.
y
x
A(0, 0)
B(4, 0)
D(0, 4)
C
S
(3, 2)
FIGURE 1
The optimal solution occurs at C(3, 2).
4.1 The Simplex Method: Standard Maximization Problems
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 202
4.1 THE SIMPLEX METHOD: STANDARD MAXIMIZATION PROBLEMS 203
Observe that the left-hand side of this equation is always less than or equal to the right-
hand side. Therefore, by adding a nonnegative variable u to the left-hand side to com-
pensate for this difference, we obtain the equality
2x 3y u 12
For example, if x 1 and y 1 [you can see by referring to Figure 1 that the
point (1, 1) is a feasible point of S], then u 7, because
2(1) 3(1) 7 12
If x 2 and y 1 [the point (2, 1) is also a feasible point of S], then u 5,
because
2(2) 3(1) 5 12
The variable u is a slack variable.
Similarly, the inequality 2x y 8 is converted into the equation 2x y
√ 8 through the introduction of the slack variable √. System (2) of linear inequali-
ties may now be viewed as the system of linear equations
2x 3y u 12
2x y √ 8
where x, y, u, and √ are all nonnegative.
Finally, rewriting the objective function (1) in the form 3x 2y P 0, where
the coefficient of P is 1, we are led to the following system of linear equations:
2x 3y u 12
2x y √ 8 (3)
3x 2y P 0
Since System (3) consists of three linear equations in the five variables x, y, u,
√, and P, we may solve for three of the variables in terms of the other two. Thus,
there are infinitely many solutions to this system expressible in terms of two param-
eters. Our linear programming problem is now seen to be equivalent to the follow-
ing: From among all the solutions of System (3) for which x, y, u, and √ are non-
negative (such solutions are called feasible solutions), determine the solution(s)
that maximizes P.
The augmented matrix associated with System (3) is
Nonbasic variables Basic variables
앗앗앗앗앗
Column of constants
xyu√ P
앗
2 3100 12 (4)
2 1010 8
冤
3 2001
冨
0
冥
Observe that each of the u-, √-, and P-columns of the augmented matrix (4) is a unit
column (see page 80). The variables associated with unit columns are called basic
variables; all other variables are called nonbasic variables.
Now, the configuration of the augmented matrix (4) suggests that we solve
for the basic variables u, √, and P in terms of the nonbasic variables x and y, obtaining
u 12 2x 3y
√ 8 2x y (5)
P 3x 2y
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 203

R
2
⎯→
1
2
Of the infinitely many feasible solutions obtainable by assigning arbitrary non-
negative values to the parameters x and y, a particular solution is obtained by letting
x 0 and y 0. In fact, this solution is given by
x 0 y 0 u 12 √ 8 P 0
Such a solution, obtained by setting the nonbasic variables equal to zero, is called a
basic solution of the system. This particular solution corresponds to the corner point
A(0, 0) of the feasible set associated with the linear programming problem (see Fig-
ure 1). Observe that P 0 at this point.
Now, if the value of P cannot be increased, we have found the optimal solution to
the problem at hand. To determine whether the value of P can in fact be improved,
let’s turn our attention to the objective function in (1). Since the coefficients of both x
and y are positive, the value of P can be improved by increasing x and/or y—that is,
by moving away from the origin. Note that we arrive at the same conclusion by
observing that the last row of the augmented matrix (4) contains entries that are neg-
ative. (Compare the original objective function, P 3x 2y, with the rewritten objec-
tive function, 3x 2y P 0.)
Continuing our quest for an optimal solution, our next task is to determine
whether it is more profitable to increase the value of x or that of y (increasing x and y
simultaneously is more difficult). Since the coefficient of x is greater than that of y, a
unit increase in the x-direction will result in a greater increase in the value of the
objective function P than a unit increase in the y-direction. Thus, we should increase
the value of x while holding y constant. How much can x be increased while holding
y 0? Upon setting y 0 in the first two equations of System (5), we see that
u 12 2x
√ 8 2x
(6)
Since u must be nonnegative, the first equation of System (6) implies that x cannot
exceed , or 6. The second equation of System (6) and the nonnegativity of √ implies
that x cannot exceed , or 4. Thus, we conclude that x can be increased by at most 4.
Now, if we set y 0 and x 4 in System (5), we obtain the solution
x 4 y 0 u 4 √ 0 P 12
which is a basic solution to System (3), this time with y and √ as nonbasic variables.
(Recall that the nonbasic variables are precisely the variables that are set equal to
zero.)
Let’s see how this basic solution may be found by working with the augmented
matrix of the system. Since x is to replace √ as a basic variable, our aim is to find an
augmented matrix that is equivalent to the matrix (4) and has a configuration in which
the x-column is in the unit form
0
1
冤
0
冥
replacing what is presently the form of the √-column in augmented matrix (4). This
may be accomplished by pivoting about the circled number 2.
8
2
12
2
204 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
xyu√ P Const. xyu√ P Const.
(7)
£
2 3100
1
1
2
0
1
2
0
3 2001
†
12
4
0
§£
2 3100
2 1010
3 2001
†
12
8
0
§
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 204

xyu√ P Const.
(8)
Using System (8), we now solve for the basic variables x, u, and P in terms of the
nonbasic variables y and √, obtaining
Setting the nonbasic variables y and √ equal to zero gives
x 4 y 0 u 4 √ 0 P 12
as before.
We have now completed one iteration of the simplex procedure, and our search
has brought us from the feasible corner point A(0, 0), where P 0, to the feasible cor-
ner point B(4, 0), where P attained a value of 12, which is certainly an improvement!
(See Figure 2.)
Before going on, let’s introduce the following terminology. The circled element 2
in the first augmented matrix of (7), which was to be converted into a 1, is called a
pivot element. The column containing the pivot element is called the pivot column.
The pivot column is associated with a nonbasic variable that is to be converted to a
basic variable. Note that the last entry in the pivot column is the negative number with
the largest absolute value to the left of the vertical line in the last row—precisely the
criterion for choosing the direction of maximum increase in P.
The row containing the pivot element is called the pivot row. The pivot row can
also be found by dividing each positive number in the pivot column into the corre-
sponding number in the last column (the column of constants). The pivot row is the
one with the smallest ratio. In the augmented matrix (7), the pivot row is the second
row because the ratio , or 4, is less than the ratio , or 6. (Compare this with the
earlier analysis pertaining to the determination of the largest permissible increase in
the value of x.)
The following is a summary of the procedure for selecting the pivot element.
Continuing with the solution to our problem, we observe that the last row of the
augmented matrix (8) contains a negative number—namely, . This indicates that P
1
2
Selecting the Pivot Element
1. Select the pivot column: Locate the most negative entry to the left of the
vertical line in the last row. The column containing this entry is the
pivot
column
. (If there is more than one such column, choose any one.)
2. Select the pivot row: Divide each positive entry in the pivot column into its
corresponding entry in the column of constants. The
pivot row is the row
corresponding to the smallest ratio thus obtained. (If there is more than one
such entry, choose any one.)
3. The
pivot element is the element common to both the pivot column and the
pivot row.
12
2
8
2
P 12
1
2
y
3
2
√
u 4 2 y √
x 4
1
2
y
1
2
√
£
0
1
0
2
1
2
1
2
1
0
0
1
1
2
3
2
0
0
1
3
4
4
12
§
R
1
2R
2
⎯⎯⎯→
R
3
3R
2
4.1 THE SIMPLEX METHOD: STANDARD MAXIMIZATION PROBLEMS 205
y
x
A(0, 0)
B(4, 0)
D(0, 4)
C
S
(3, 2)
FIGURE 2
One iteration has taken us from A(0, 0),
where P 0, to B(4, 0), where P 12.
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 205
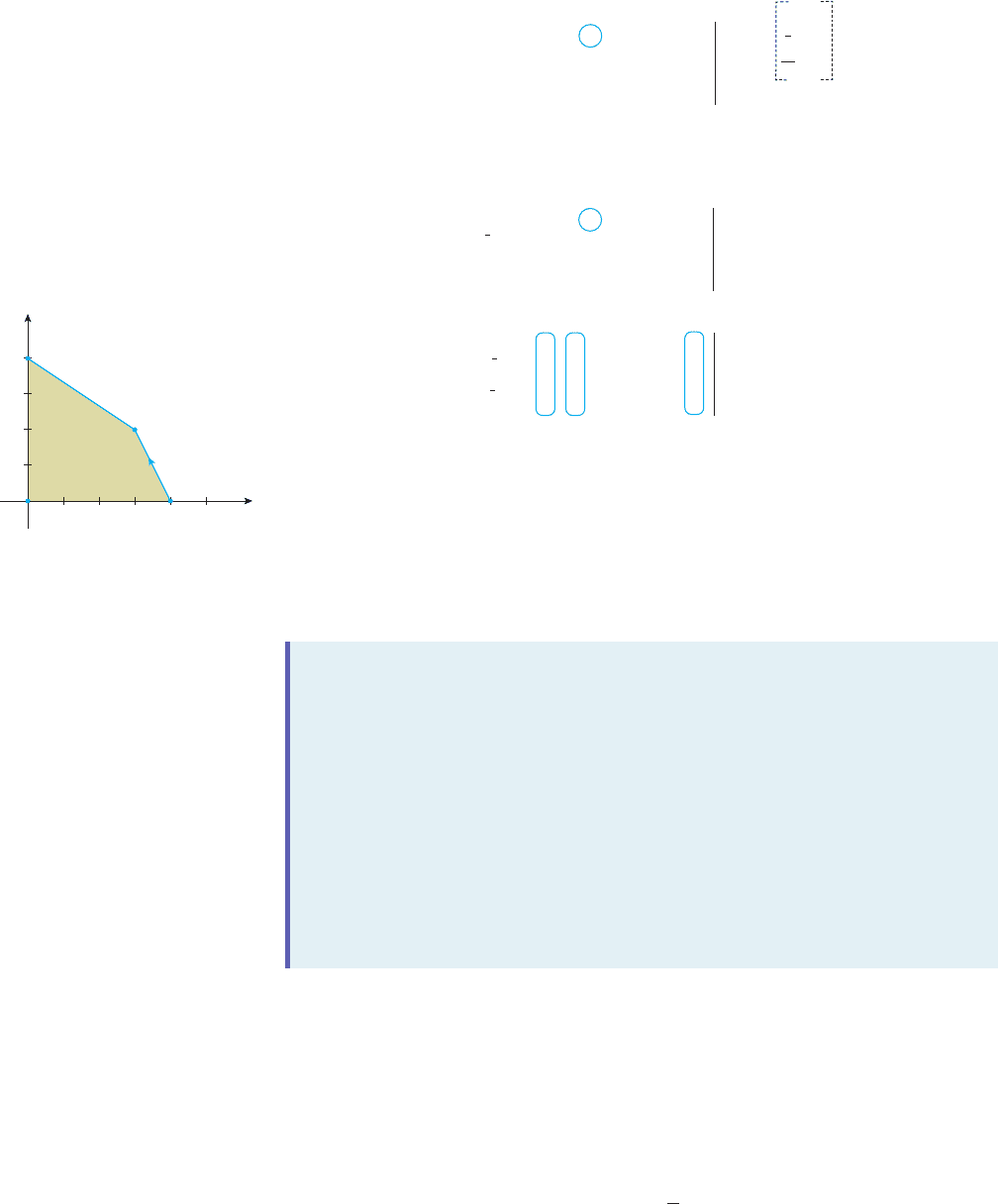
206 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
is not maximized at the feasible corner point B(4, 0), so another iteration is required.
Without once again going into a detailed analysis, we proceed immediately to the
selection of a pivot element. In accordance with the rules, we perform the necessary
row operations as follows:
Interpreting the last augmented matrix in the usual fashion, we find the basic solu-
tion x 3, y 2, and P 13. Since there are no negative entries in the last row, the
solution is optimal and P cannot be increased further. The optimal solution is the fea-
sible corner point C(3, 2) (Figure 3). Observe that this agrees with the solution we
found using the method of corners in Section 3.3.
Having seen how the simplex method works, let’s list the steps involved in the
procedure. The first step is to set up the initial simplex tableau.
EXAMPLE 1
Set up the initial simplex tableau for the linear programming prob-
lem posed in Example 1, Section 3.2.
Solution
The problem at hand is to maximize
P x 1.2y
or, equivalently,
P x
6
5
y
Setting Up the Initial Simplex Tableau
1. Transform the system of linear inequalities into a system of linear equations
by introducing slack variables.
2. Rewrite the objective function
P c
1
x
1
c
2
x
2
c
n
x
n
in the form
c
1
x
1
c
2
x
2
c
n
x
n
P 0
where all the variables are on the left and the coefficient of P is 1. Write
this equation below the equations of step 1.
3. Write the tableau associated with this system of linear equations.
y
x
A(0, 0)
B(4, 0)
D(0, 4)
C
S
(3, 2)
FIGURE 3
The next iteration has taken us from
B(4, 0), where P 12, to C(3, 2), where
P 13.
xyu√ P
02110 4
1
1
2
0
1
2
04
冤
0
1
2
0
3
2
112
冥
xyu√ P
01
1
2
1
2
02
1
1
2
0
1
2
04
冤
0
1
2
0
3
2
112
冥
xy u √ P
01
1
2
1
2
02
10
1
4
3
4
03
冤
00
1
4
5
4
113
冥
Pivot
씮
row
앖
Pivot
column
Ratio
4
1/2
8
4
2
2
R
1
⎯→
1
2
R
2
R
1
⎯⎯⎯→
R
3
R
1
1
2
1
2
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 206

subject to
(9)
This is a standard maximization problem and may be solved by the simplex
method. Since System (9) has two linear inequalities (other than x 0, y 0), we
introduce the two slack variables u and √ to convert it to a system of linear equations:
2x y u 180
x 3y √ 300
Next, by rewriting the objective function in the form
where the coefficient of P is 1, and placing it below the system of equations, we
obtain the system of linear equations
2x y u 180
x 3y √ 300
x y P 0
The initial simplex tableau associated with this system is
xyu√ P Constant
2 1100 180
1 3010 300
1
6
5
001 0
Before completing the solution to the problem posed in Example 1, let’s summarize
the main steps of the simplex method.
The Simplex Method
1. Set up the initial simplex tableau.
2. Determine whether the optimal solution has been reached by examining all
entries in the last row to the left of the vertical line.
a. If all the entries are nonnegative, the optimal solution has been reached.
Proceed to step 4.
b. If there are one or more negative entries, the optimal solution has not been
reached. Proceed to step 3.
3. Perform the pivot operation. Locate the pivot element and convert it to a 1
by dividing all the elements in the pivot row by the pivot element. Using row
operations, convert the pivot column into a unit column by adding suitable
multiples of the pivot row to each of the other rows as required. Return to
step 2.
4. Determine the optimal solution(s). The value of the variable heading each
unit column is given by the entry lying in the column of constants in the row
containing the 1. The variables heading columns not in unit form are assigned
the value zero.
6
5
x
6
5
y P 0
x 0, y 0
x 3y 300
2x y 180
4.1 THE SIMPLEX METHOD: STANDARD MAXIMIZATION PROBLEMS 207
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 207
EXAMPLE 2
Complete the solution to the problem discussed in Example 1.
Solution
The first step in our procedure, setting up the initial simplex tableau, was
completed in Example 1. We continue with Step 2.
Step 2 Determine whether the optimal solution has been reached. First, refer to the
initial simplex tableau:
xyu√ P Constant
2 1100 180
(10)
1 3010 300
1
6
5
001 0
Since there are negative entries in the last row of the initial simplex tableau,
the initial solution is not optimal. We proceed to Step 3.
Step 3 Perform the following iterations. First, locate the pivot element:
a. Since the entry is the most negative entry to the left of the vertical
line in the last row of the initial simplex tableau, the second column in
the tableau is the pivot column.
b. Divide each positive number of the pivot column into the corresponding
entry in the column of constants and compare the ratios thus obtained. We
see that the ratio is less than the ratio
so row 2 is the pivot row.
c. The entry 3 lying in the pivot column and the pivot row is the pivot element.
Next, we convert this pivot element into a 1 by multiplying all the
entries in the pivot row by . Then, using elementary row operations, we
complete the conversion of the pivot column into a unit column. The details
of the iteration follow:
xyu√ P Constant
2 1100 180
1 3010 300
1
6
5
001 0
xyu√ P Constant
2 1100 180
1
3
10
1
3
0 100
1
6
5
001 0
xyu √ P Constant
5
3
01
1
3
080
(11)
1
3
10
1
3
0 100
3
5
00
2
5
1 120
This completes one iteration. The last row of the simplex tableau contains a
negative number, so an optimal solution has not been reached. Therefore,
we repeat the iterative step once again, as follows:
1
3
180
1
,
300
3
6
5
208 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
Pivot
씮
row
앖
Pivot
column
Ratio
300
3
100
180
1
180
R
2
⎯→
1
3
R
1
R
2
⎯⎯⎯→
R
3
R
2
6
5
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 208

xyu √ P Constant
5
3
01
1
3
080
1
3
10
1
3
0 100
3
5
00
2
5
1 120
xyu √ P Constant
10
3
5
1
5
048
1
3
10
1
3
0 100
3
5
00
2
5
1 120
xy u √ P Constant
10
3
5
1
5
048
(12)
01
1
5
2
5
084
00
2
9
5
2
7
5
1 148
4
5
The last row of the simplex tableau (12) contains no negative numbers, so
we conclude that the optimal solution has been reached.
Step 4 Determine the optimal solution. Locate the basic variables in the final tableau.
In this case the basic variables (those heading unit columns) are x, y, and P.
The value assigned to the basic variable x is the number 48, which is the entry
lying in the column of constants and in row 1 (the row that contains the 1).
xy u √ P Constant
10
3
5
1
5
048
01
1
5
2
5
084
00
2
9
5
2
7
5
1 148
4
5
Similarly, we conclude that y 84 and P 148.8. Next, we note that the
variables u and √ are nonbasic and are accordingly assigned the values u 0
and √ 0. These results agree with those obtained in Example 1, Section 3.3.
EXAMPLE 3
Maximize P 2x 2y z
subject to 2x y 2z 14
2x 4y z 26
x 2y 3z 28
x 0, y 0, z 0
Solution
Introducing the slack variables u, √, and w and rewriting the objective
function in the standard form gives the system of linear equations
2x y 2z u 14
2x 4y z √ 26
x 2y 3z w 28
2x 2y z P 0
4.1 THE SIMPLEX METHOD: STANDARD MAXIMIZATION PROBLEMS 209
Ratio
100
1/3
300
80
5/3
48
Pivot
씮
row
앖
Pivot
column
R
1
⎯→
3
5
R
2
R
1
⎯⎯⎯→
R
3
R
1
3
5
1
3
씯
씯
—
씯
—
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 209
The initial simplex tableau is given by
Since the most negative entry in the last row (2) occurs twice, we may choose either
the x- or the y-column as the pivot column. Choosing the x-column as the pivot column
and proceeding with the first iteration, we obtain the following sequence of tableaus:
Since there is a negative number in the last row of the simplex tableau, we perform
another iteration, as follows:
210 4 LINEAR PROGRAMMING: AN ALGEBRAIC APPROACH
Ratio
28
1
28
26
2
13
14
2
7
Pivot
씮
row
앖
Pivot
column
R
2
2R
1
⎯⎯⎯→
R
3
R
1
R
4
2R
1
R
1
⎯→
1
2
xyzu√ wP Constant
2 1 21000 14
2 4 10100 26
1 2 30010 28
2 2 10001 0
xyzu√ wP Constant
2 1 21000 14
2 4 10100 26
1 2 30010 28
2 2 10001 0
xyzu√ wP Constant
1
1
2
1
1
2
000 7
2 4 10100 26
1 2 30010 28
2 2 10001 0
xyzu√ wP Constant
1
1
2
1
1
2
000 7
031 1100 12
0
3
2
2
1
2
010 21
0 1 1 1001 14
xyzu√ wP Constant
1
1
2
1
1
2
000 7
031 1100 12
0
3
2
2
1
2
010 21
0 1 1 1001 14
xyzu√ wP Constant
1
1
2
1
1
2
000 7
01
1
3
1
3
1
3
00 4
0
3
2
2
1
2
010 21
0 1 1 1001 14
xy z u √ wP Constant
10
7
6
2
3
1
6
00 5
01
1
3
1
3
1
3
00 4
00
5
2
0
1
2
10 15
00
2
3
2
3
1
3
01 18
Ratio
21
3/2
14
12
3
4
7
1/2
14
Pivot
씮
row
앖
Pivot
column
R
1
R
2
⎯⎯⎯→
R
3
R
2
R
4
R
2
3
2
1
2
R
2
⎯→
1
3
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 210

All entries in the last row are nonnegative, so we have reached the optimal solution.
We conclude that x 5, y 4, z 0, u 0, √ 0, w 15, and P 18.
The following example is constructed to illustrate the geometry associated with the
simplex method when used to solve a problem in three-dimensional space. We sketch
the feasible set for the problem and show the path dictated by the simplex method in
arriving at the optimal solution for the problem. The use of a calculator will help in
the arithmetic operations if you wish to verify the steps.
EXAMPLE 4
Geometric Illustration of Simplex Method in 3-Space
Maximize P 20x 12y 18z
subject to 3x y 2z 9
2x 3y z 8
x 2y 3z 7
x 0, y 0, z 0
Solution
Introducing the slack variables u, √, and w and rewriting the objective
function in standard form gives the following system of linear equations:
3x y 2z u 9
2x 3y z √ 8
x 2y 3z w 7
20x 12y 18z P 0
The initial simplex tableau is given by
4.1 THE SIMPLEX METHOD: STANDARD MAXIMIZATION PROBLEMS 211
Explore & Discuss
Consider the linear programming problem
Maximize P x 2y
subject to 2x y 4
x 3y 3
x 0, y 0
1. Sketch the feasible set S for the linear programming problem and explain why the prob-
lem has an unbounded solution.
2. Use the simplex method to solve the problem as follows:
a. Perform one iteration on the initial simplex tableau. Interpret your result. Indicate the
point on S corresponding to this (nonoptimal) solution.
b. Show that the simplex procedure breaks down when you attempt to perform another
iteration by demonstrating that there is no pivot element.
c. Describe what happens if you violate the rule for finding the pivot element by allow-
ing the ratios to be negative and proceeding with the iteration.
xyzu√ wP Constant
3 1 21000 9
2 3 10100 8
1 2 30010 7
20 12 180001 0
87533_04_ch4_p201-256 1/30/08 9:51 AM Page 211
