Стронгин Р.Г (ред.) Высокопроизводительные параллельные вычисления на кластерных системах

Подождите немного. Документ загружается.

f(x

)=0

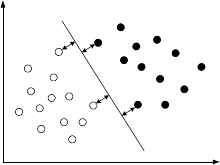
Рис. 1

Уравнение разделяющей плоскости имеет следующий вид (для d-

мерного пространства признаков объектов):

+ w

+ ... + w

+ w

= 0,

где d – размерность пространства признаков;

W=(w

, w

, ..., w

) – направляющий вектор;

– скалярный порог.

Или в векторной форме:

(W, X) + w

= 0.

В методе опорных векторов выделяют два этапа: этап обучения и

этап распознавания. На первом этапе из множества обучающих

примеров отбираются опорные векторы, на основе которых строится

разделяющая плоскость. Этап распознавания заключается в том, что на

вход полученного классификатора подается пример Х, о классовой

принадлежности которого ничего неизвестно. Классификатор должен

выдать

ответ, к какому классу относится вектор Х.

Проблема использования метода SVM заключается в том, что его

обучение сводится к решению задачи квадратичной оптимизации с

предельными ограничивающими условиями и одним ограничением

линейного равенства. Общие методы решения таких задач известны,

но довольно трудоёмки как в смысле реализации, так и по времени

выполнения.

На

данный момент разработано достаточно много алгоритмов

обучения SVM. Можно выделить следующие группы методов [2].

1. Традиционные методы решения оптимизационных задач,

которые применяются в общем случае и для обучения искусственных

нейронных сетей.

Применительно к SVM данные методы используются, когда

количество обучающих примеров относительно невелико (до 4000 –

5000). К этой группе относятся различные методы поиска седловой

точки функции Лагранжа – методы Ньютона, квазиньютоновские

методы, методы сопряженных направлений и др.

2. Методы декомпозиции – методы обучения SVM, идея которых

основана на разбиении одной большой задачи на ряд подзадач.

Главным преимуществом

данного подхода является то, что он

предлагает алгоритмы с требованиями памяти, которые линейны

относительно количества обучающих примеров и количества опорных

векторов.

Первый подход по разбиению больших задач обучения SVM на

серии меньших задач оптимизации известен как алгоритм

«образования фрагментов» (chunking). Алгоритм начинает со

случайного подмножества обучающих данных, решает эту задачу и

многократно добавляет примеры, которые нарушают условия

оптимальности.

В группе методов декомпозиции наиболее эффективен на сегодня

алгоритм последовательной минимальной оптимизации (Sequential

Minimal Optimization, SMO), предложенный Платтом [3]. Его можно

рассматривать как отдельный случай алгоритма декомпозиции, размер

рабочего набора в котором всегда равен 2, а для поиска оптимального

рабочего набора используется набор эвристик.

К этой же группе можно

отнести и методы, основанные на

аппроксимации гессенской матрицы (матрицы частных производных

функции Лагранжа) с помощью более мелких матриц с

использованием или низкоуровневого представления, или

выборки/дискретизации, тем самым уменьшается размер задачи

оптимизации и ускоряется процесс обучения.

3. Методы обучения, основанные на вычленении из большого

набора входных данных тех векторов, которые являются

опорными,

поскольку только они определяют оптимальное решение

оптимизационной задачи для SVM. Сюда же можно отнести и так

называемые инкрементные методы обучения, которые предполагают

последовательное обучение SVM на новых данных при удалении всех

предыдущих данных за исключением их опорных векторов.

Преимуществом инкрементных методов является возможность

быстрого переобучения SVM при появлении новых данных.

Алгоритм распараллеливания процесса обучения SVM

В данном разделе предложен метод, позволяющий ускорить

процесс обучения SVM. Непосредственно перед началом обучения

метод позволяет сократить количество данных в исходном наборе. На

данном этапе алгоритм использует распараллеливание вычислений на

основе разделения данных на независимые блоки произвольным

образом.

Рассмотрим алгоритм в случае разделения набора обучающих

данных на

два класса линейной гиперплоскостью.

Шаг 1.

Пусть имеется N процессоров, разобьем весь обучающий набор

примеров на N равных частей, в каждой из которых будут

присутствовать примеры каждого класса в тех же пропорциях, что и в

исходном наборе. Затем на каждом процессоре выполним обучение

SVM со своим набором входных данных. По окончании этих действий

будем

исключать из исходного набора данных те обучающие примеры,

которые оказались за пределами разделяющей полосы во всех случаях.

Иными словами, отбрасываем примеры, которые не являются

опорными векторами для всех N полученных классификаторов.

Если обучающий набор все еще велик для обучения SVM с

использованием одного процессора, можно повторить выполнение

шага 1.

Шаг 2.

Выполняем обучение SVM на

одном процессоре с использованием

обучающего набора, полученного после выполнения первого шага.

Данный алгоритм распараллеливания не привязан к конкретному

методу обучения SVM. Однако он имеет следующую особенность.

При большом количестве процессоров скорость уменьшения

обучающего набора снижается, следовательно, первый шаг нужно

выполнять большее число раз.

Рассмотрим предложенный алгоритм на примере.

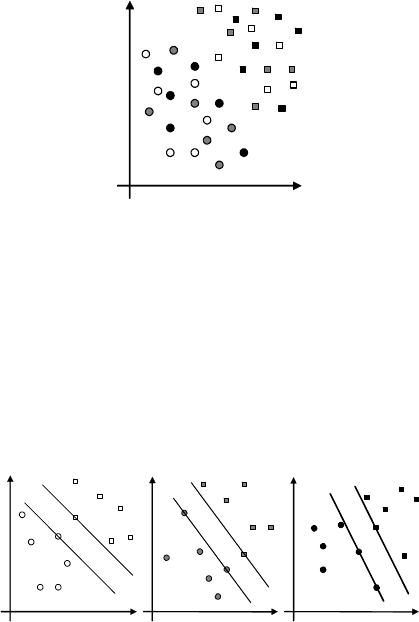
Пусть имеется два

класса обучающих объектов – круглые и

квадратные. Будет обучать SVM при помощи трех процессоров.

Разобьем исходные данные на 3 группы: первому процессору – белые,

второму – серые и третьему – черные (рис. 2).

Рис. 2

После того, как каждый процессор обработает свои данные, в

каждом наборе будет своя максимальная разделяющая полоса (см.

рис. 3). Те элементы из исходного набора данных, которые попали

хотя бы в одну из полученных разделяющих полос или лежат на их

границе, могут являться опорными для всего набора данных,

остальные элементы можно отбросить, так

как они оказались

«бесполезными» во всех трех случаях (рис. 4). Первый шаг закончен, в

случае недостаточного уменьшения набора обучающих примеров его

можно повторить.

а)

б)

в)

Рис. 3

Рис. 4

По завершении первого шага, когда набор исходных данных был

существенно сокращен, нужно обучить SVM на этом наборе. Как

видно из примера, при поиске окончательного решения использовался

набор данных (рис. 5), сравнимый по количеству элементов с

наборами, полученными при начальном разбиении исходных данных

на первом шаге.

Рис. 5

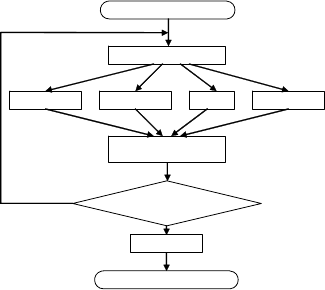
Блок-схема алгоритма распараллеливания представлена на рис. 6.

Начало

Разбиение данных

Обучение

SVM

Обучение

SVM

…

Обучение

SVM

Исключение заведомо

неопо

ных векто

ов

Обучение

SVM

Коне

Нужно

дальнейшее

да

Рис. 6

Заключение

Преимуществом предложенного алгоритма является то, что он не

зависит от метода обучения SVM и может использовать наиболее

подходящий метод в каждом конкретном случае.

К особенностям алгоритма можно отнести снижение объема

сокращаемых данных за одну итерацию при увеличении числа

процессоров. При этом следует учитывать соотношение между

временем, затрачиваемым на выполнение одной итерации

алгоритма

при заданном числе процессоров, и количеством этих итераций.

Литература

1. Vapnik V. N. The Nature of Statistical Learning Theory. Springer–

Verlag, 1995.

2. Котельников Е. В., Ямшанов М. Л. Метод Support Vector

Machine для решения задач классификации // Вестник

ВятГГУ. Информатика, математика, язык. №4. 2007. – С. 55–

61.

3. Platt J. Sequential Minimal Optimization: A Fast Algorithm for

Training Support Vector Machines. 1998.

РАСПАРАЛЛЕЛИВАНИЕ МЕТОДА ВЕТВЕЙ И ГРАНИЦ

РЕШЕНИЯ КОНВЕЙЕРНОЙ ЗАДАЧИ ПОСТРОЕНИЯ

ОПТИМАЛЬНОГО ПО БЫСТРОДЕЙСТВИЮ РАСПИСАНИЯ

В.С. Власов

Нижегородский государственный университет

Рассмотрим конвейерную задачу построения оптимального по

быстродействию расписания последовательного выполнения n работ

на m станках. Пусть i - номер станка, j - номер работы, T = ||t

||- m

действительная матрица, элемент t

которой - определяет время

выполнения работы j на станке i,

mi ,1=

nj ,1=

. Требуется найти

такую матрицу X = ||x

||- размерами m

n, для которой выполняются

ограничения:

jijiij

txx

11 −−

+≥

mi ,2=

nj ,1=

, (1)

ikikij

txx +≥

или

ijijik

txx

≥

mi ,1=

nj ,1=

nk ,1=

, (2)

Если

ikij

xx ≥

, то

sksj

xx ≥

mi ,1=

ms ,1=

nj ,1=

, (3)

0≥

mi ,1=

nj ,1=

, (4)

и достигает минимального значения критерий

)(max)(

mjmj

txXF

. (5)

Здесь x

- момент начала выполнения работы j на станке i,

mi ,1=

nj ,1=

, условия (1) означают, что выполнение работы на станке может

начаться не раньше, чем эта работа завершится на предыдущем станке,

условия (2) означают, что на станке одновременно не может

выполняться более одной работы, условия (3) означают, что порядок

выполнения работ одинаков на всех станках (конвейерность

расписания), а условия (4) являются естественными условиями на

переменные. Каждому

допустимому решению соответствует своя

перестановка, определяющая порядок выполнения работ на станках.

Рассматриваемая задача относится к классу NP-трудных.

В основе решения рассматриваемой задачи предлагается

использовать алгоритм, основанный на идеологии метода ветвей и

границ. Основные процедуры метода ветвей и границ к решению

конвейерной задачи теории расписаний.

Процедура оценок включает в себя определение верхней

(достижимой) оценки V и нижней оценки H.

Для нахождения точного решения предлагается использовать

следующую схему.

Так как конвейерное расписание в рассмотренной постановке

однозначно определяется перестановкой из n элементов, то это

позволяет для нахождения приближенных решений использовать

многие известные алгоритмы, например, такие как Simulated Annealing

(SA), Ant Colony Algorithm (AC), Genetic Algorithms (GA) [1].

Формируем множество Ф(А), которое содержит все

перечисленные алгоритмы, позволяющие работать с перестановками.

Параллельно запуская предложенные алгоритмы, определяем

приближенные решения рассматриваемой задачи.

Тогда верхняя оценка V на каждом шаге будет определяться как

лучшее (наименьшее) значение критерия (5), полученное в результате

работы одного из алгоритмов. Это позволит уменьшить достижимое

значение верхней оценки и

существенно сократить множество

ветвлений.

Для определения нижней оценки Н предлагается следующая

схема:

Для определения нижней оценки на первом шаге:

∑∑

−

min

mjij

,nj

t tH

. (6.1)

Для определения нижней оценки с учетом того, что работа k

поставлена в расписание первой:

kjttH

mjik

≠+=

∑∑

. (6.2)

Для определения нижней оценки с учетом того, что в расписание

поставлены работы k и l:

∑∑

≠≠+++=

mjml

ljkjttlkDiftH

,,),(

, (6.3)

где функция

),( lkDif

определяет задержку начала выполнения

работы l на станке m после выполнения на нем работы k и

определяется как:

⎩

⎨

⎧

+−++++

−

−−−−

иначе )},()),((,0{max

1,i если,0

),(

,1,1,1,1 ikik

lilikiki

txlkDiftxtx

lkDif

Для определения нижней оценки с учетом того, что в расписание

поставлены работы k, l и s:

∑∑

≠≠≠+++++=

mjms

kls

sjljkjttslDiftlkDiftH

,,,),().(

(6.4)

и т.д.

Процедура ветвления рассматривает все допустимые варианты

построения перестановок.

Процедура отсева предполагает, что если значение верхней

(достижимой) оценки в одной из вершин дерева ветвлений не больше

значения нижней оценки в другой вершине, то вторая вершина

исключается из рассмотрения.

Процедура останова определяет окончание процесса вычислений.

Если осталась неотброшенной

лишь одна вершина, в которой значения

оценок совпадают, то найдено оптимальное решение задачи, которое

определяется перестановкой, соответствующей верхней оценке.

Таким образом, общая предложенная в работе схема решения

конвейерной задачи построения оптимального по быстродействию

расписания с использованием процедур метода ветвей и границ

включает в себя следующие шаги:

1. Определение верхних оценок. Используя

независимые друг

от друга алгоритмы (такие как SA, AC, GA), в каждой

вершине дерева ветвления метода ветвей и границ

параллельно определяют верхние (достижимые) оценки, из

которых в дальнейших вычислениях используется

минимальная.

2. Определение нижних оценок. В каждой вершине в

зависимости от тех работ, которые уже включены в

расписание, используются соотношения типа (6) для

вычисления

нижней оценки.

3. Процедуры отсева и останова применяются по общей схеме.

Для большеразмерных задач в случае ограниченности

вычислительных ресурсов метод может быть остановлен, и лучшая из

найденных верхних (достижимых) оценок будет являться

приближенным решением.

Литература

1. Прилуцкий М.Х., Власов В.С. Метод комбинирования

эвристических алгоритмов для конвейерных задач теории

расписаний // Электронный журнал "Исследовано в России",

086, стр. 901-905, 2007.

http://zhurnal.ape.relarn.ru/articles/2007/086.pdf

2. Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by

simulated annealing.

3. Dorigo M., Maniezzo V., Colorni A. The Ant System:

Optimization by a colony of cooperating objects // IEEE

Transactions on Systems, Man, and Cybernetics. – Part B, 26(1),

1996. Р. 29- 41.

4. Макконнел Дж. Основы современных алгоритмов. Изд.

“Техносфера”, 2004.

Контакты

vlasov_nn@mail.ru

ИСПОЛЬЗОВАНИЕ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛЕНИЙ

В ГЕНЕТИЧЕСКИХ АЛГОРИТМАХ

К.А. Генералов

Пензенский государственный университет

Генетические алгоритмы являются альтернативным инструментом

исследования многоэкстремальных функций. Первый генетический

алгоритм, положивший основу всем существующим генетическим

алгоритмам, был предложен Джоном Холландом (John Holland) в 1975

году и носил название “репродуктивный план Холланда”.

На данный момент предложен ряд стратегий параллельного

выполнения генетических алгоритмов. В работах [1, 3] выделены

следующие типы параллелизма генетических алгоритмов:



глобальный параллелизм;

 миграционная (островная) модель;

 клеточная модель [3];

 диффузионная модель.

Рассмотрим каждый вид параллелизма более подробно.