Stone M., Goldbart P. Mathematics for Physics: A Guided Tour for Graduate Students

Подождите немного. Документ загружается.

15.3 Lie algebras 565



–7

–4

–1

0–4 –3 –2 –1 2 413

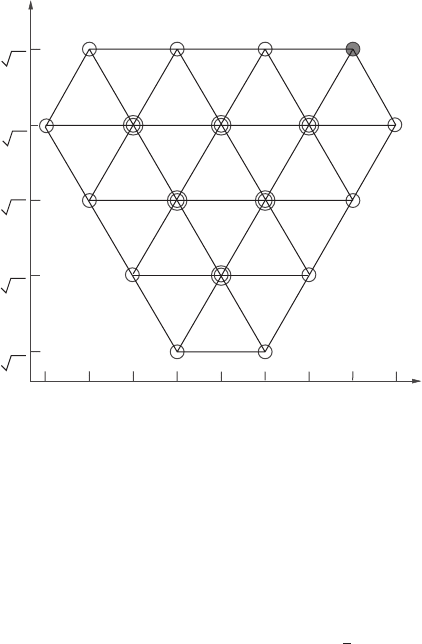
Figure 15.3 The weight diagram of the 24-dimensional irrep with p = 3, q = 1. The highest

weight is shaded.

obvious. We will therefore restrict ourselves to describing the outcome of this procedure

without giving proofs.

What we find is that the weights in a finite-dimensional representation of su(3) form

a hexagonally symmetric “crystal” lying on a triangular lattice, and the representations

may be labelled by pairs of integers (zero allowed) p, q which give the length of the sides

of the crystal. These representations have dimension d =

(p + 1)(q + 1)(p + q + 2).

Figure 15.3 shows the set of weights occurring in the representation of SU(3) with

p = 3 and q = 1. Each circle represents a state, whose weight (λ

, λ

) may be read off

from the displayed axes. A double circle indicates that there are two linearly independent

vectors with the same weight. A count confirms that the number of independent weights,

and hence the dimension of the representation, is 24. For SU(3) representations the

degeneracy – i.e. the number of states with a given weight – increases by unity at

each “layer” until we reach a triangular inner core, all of whose weights have the same

degeneracy.

In particle physics applications, representations are often labelled by their dimension.

The defining representation of SU(3) and its complex conjugate are denoted by 3 and

3 (see Figure 15.4), while the weight diagrams of the adjoint representation 8 and the

representation 10 have shapes shown in Figure 15.5.

Cartan algebras: Roots and co-roots

For a general simple Lie algebra we may play the same game. We first find a maximal

linearly independent set of commuting generators h

. These h

form a basis for the Cartan

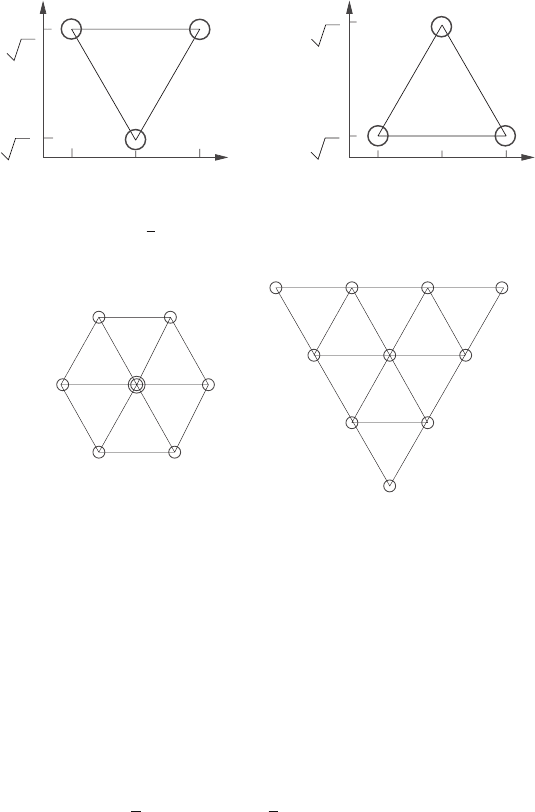
566 15 Lie groups



–1 10

–1

–2

Figure 15.4 The weight diagrams of the irreps with p = 1, q = 0, and p = 0, q = 1, also known,

respectively, as the 3 and the

Figure 15.5 The irreps 8 (the adjoint) and 10.

algebra h, whose dimension is the rank of the Lie algebra. We next find ladder operators

by diagonalizing the “ad” action of the h

on the rest of the algebra:

ad (h

=[h

, e

]=α

. (15.133)

The simultaneous eigenvectors e

are the ladder operators that change the eigenvalues of

the h

. The corresponding eigenvalues α, thought of as vectors with components α

, are

the roots, or root vectors. The roots are therefore the weights of the adjoint representation.

It is possible to put factors of “i” in appropriate places so that the α

are real, and we

will assume that this has been done. For example, in su(3) we have already seen that

= (2, 0), α

= (1,

√

3), α

= (−1,

√

3).

Here are the basic properties and ideas that emerge from this process:

(i) Since α

e

, h

=ad (h

, h

=−e

, [h

, h

] = 0, we see that h

, e

=0.

(ii) Similarly, we see that (α

+ β

)e

, e

=0, so the e

are orthogonal to one

another unless α +β = 0. Since our Lie algebra is semisimple, and consequently

the Killing form non-degenerate, we deduce that if α is a root, so is −α.

(iii) Since the Killing form is non-degenerate, yet the h

are orthogonal to all the e

it must also be non-degenerate when restricted to the Cartan algebra. Thus, the

metric tensor, g

=h

, h

, must be invertible with inverse g

. We will use the

notation α · β to represent α

15.3 Lie algebras 567

(iv) If α, β are roots, then the Jacobi identity shows that

, [e

, e

]] = (α

+ β

)[e

, e

so if [e

, e

] is non-zero then α + β is also a root, and [e

, e

]∝e

α+β

(v) It follows from (iv) that [e

, e

−α

] commutes with all the h

, and since h was

assumed maximal, it must either be zero or a linear combination of the h

. A short

calculation shows that

h

, [e

, e

−α

] = α

e

, e

−α

,

and, since e

, e

−α

 does not vanish, [e

, e

−α

] is non-zero. We can therefore

choose to normalize the e

±α

so that

, e

−α

2α

def

= h

where α

= g

, and h

obeys

, e

±α

]=±2e

±α

The h

are called the co-roots.

(vi) The importance of the co-roots stems from the observation that the triad h

, e

±α

obeys the same commutation relations as=σ

and σ

, and so forms an su(2) subalge-

bra of g. In particular h

(being the analogue of 2J

) has only integer eigenvalues.

For example, in su(3)

, T

−

]=h

= 

, V

−

]=h



√



, U

−

]=h

=−



√



and in the defining representation

⎛

⎝

100

0 −10

000

⎞

⎠

⎛

⎝

10 0

00 0

00−1

⎞

⎠

⎛

⎝

00 0

01 0

00−1

⎞

⎠

have eigenvalues ±1.

568 15 Lie groups

(vii) Since

ad (h

=[h

, e

2α ·β

we conclude that 2α · β/α

must be an integer for any pair of roots α, β.

(viii) Finally, there can only be one e

for each root α. If not, and there were an inde-

pendent e



, we could take linear combinations so that e

−α

and e



are Killing

orthogonal, and hence [e

−α

, e



]=α

e

−α

, e



=0. Thus ad (e

−α



= 0, and



is killed by the step-down operator. It would therefore be the lowest weight

in some su(2) representation. At the same time, however, ad (h



= 2e



, and

we know that the lowest weight in any spin J representation cannot have positive

eigenvalue.

The conditions that

2α ·β

∈ Z

for any pair of roots tightly constrains the possible root systems, and is the key to

Cartan and Killing’s classification of the semisimple Lie algebras. For example the

angle θ between any pair of roots obeys cos

θ = n/4soθ can take only the values

◦

,30

◦

,45

◦

,60

◦

,90

◦

, 120

◦

, 135

◦

, 150

◦

or 180

◦

These constraints lead to a complete classification of possible root systems into the

following infinite families:

, n = 1, 2, ···. sl(n + 1, C),

, n = 2, 3, ···. so(2n + 1, C),

, n = 3, 4, ···. sp(2n, C),

, n = 4, 5, ···. so(2n, C),

together with the root systems G

, F

, E

and E

of the exceptional algebras. The

latter do not correspond to any of the classical matrix groups. For example, G

is the

root system of g

, the Lie algebra of the group G

of automorphisms of the octonions.

This group is also the subgroup of SL(7) preserving the general totally antisymmetric

trilinear form.

The restrictions on the starting values of n in these families are to avoid repeats

arising from “accidental” isomorphisms. If we allow n = 1, 2, 3, in each series, then

= D

= A

. This corresponds to sp(2, C)

∼

so(3, C)

∼

sl(2, C). Similarly, D

+ A

, corresponding to the isomorphism SO(4)

∼

SU(2) × SU(2)/Z

, while C

implies that, locally, the compact Sp(2)

∼

SO(5). Finally, D

= A

implies that

SU(4)/Z

∼

SO(6).

15.3 Lie algebras 569

15.3.4 Product representations

Given two representations 

(1)

and 

(2)

of g, we can form a new representation that

exponentiates to the tensor product of the corresponding representations of the group G.

Motivated by the result of Exercise 14.13

exp(A ⊗ I

+ I

⊗ B) = exp(A) ⊗ exp(B), (15.134)

we take the representation matrices to act on the tensor product space as



(1⊗2)

= 

(1)

⊗ I

(2)

+ I

(1)

⊗ 

(2)

. (15.135)

With this definition

[

(1⊗2)

, 

(1⊗2)

]=([

(1)

⊗ I

(2)

+ I

(1)

⊗ 

(2)

), (

(1)

⊗ I

(2)

+ I

(1)

⊗ 

(2)

)]

=[

(1)

, 

(1)

]⊗I

(2)

+[

(1)

, I

(1)

]⊗

(2)

+ 

(1)

⊗[I

(2)

, 

(2)

]+I

(1)

⊗[

(2)

, 

(2)

]

=[

(1)

, 

(1)

]⊗I

(2)

+ I

(1)

⊗[

(2)

, 

(2)

], (15.136)

showing that the 

(1⊗2)

obey the Lie algebra as required.

This process of combining representations is analogous to the addition of angular

momentum in quantum mechanics. Perhaps more precisely, the addition of angular

momentum is an example of this general construction. If representation 

(1)

has weights

(1)

, i.e. h

(1)

=m

(1)

, and 

(2)

has weights m

(2)

, then, writing |m

(1)

, m

(2)



for |m

(1)

⊗|m

(2)

, we have

(1⊗2)

(1)

, m

(2)

=(h

(1)

⊗ 1 + 1 ⊗ h

(2)

)|m

(1)

, m

(2)



= (m

(1)

+ m

(2)

)|m

(1)

, m

(2)

 (15.137)

so the weights appearing in the representation 

(1⊗2)

are m

(1)

+ m

(2)

The new representation is usually decomposable. We are familiar with this decompo-

sition for angular momentum where, if j ≥ j



j ⊗ j



= (j +j



) ⊕ (j + j



− 1) ⊕···⊕(j − j



). (15.138)

This can be understood from adding weights. For example consider adding the weights

of j = 1/2, which are m =±1/2 to those of j = 1, which are m =−1, 0, 1. We get

m =−3/2, −1/2 (twice), +1/2 (twice) and m =+3/2. These decompose as shown in

Figure 15.6.

The rules for decomposing products in other groups are more complicated than for

SU(2), but can be obtained from weight diagrams in the same manner. In SU(3),we

570 15 Lie groups

Figure 15.6 The weights for 1/2 ⊗ 1 = 3/2 ⊕ 1/2.

Figure 15.7 Adding the weights of 3 and

have, for example

3 ⊗

3 = 1 ⊕ 8,

3 ⊗ 8 = 3 ⊕

6 ⊕ 15,

8 ⊗ 8 = 1 ⊕ 8 ⊕ 8 ⊕ 10 ⊕

10 ⊕ 27. (15.139)

To illustrate the first of these we show, in Figure 15.7, the addition of the weights in

3 to each of the weights in the 3. The resultant weights decompose (uniquely) into the

weight diagrams for the 8 together with a singlet.

15.3.5 Subalgebras and branching rules

As with finite groups, a representation that is irreducible under the full Lie group or

algebra will in general become reducible when restricted to a subgroup or subalgebra.

The pattern of the decomposition is again called a branching rule . Here, we provide

some examples to illustrate the ideas.

The three operators V

and h



√



of su(3) form a Lie subalgebra that

is isomorphic to su(2) under the map that takes them to σ

and σ

, respectively. When

restricted to this subalgebra, the eight-dimensional representation of su(3) becomes

reducible, decomposing as

8 = 3 ⊕ 2 ⊕ 2 ⊕ 1, (15.140)

where the 3, 2 and 1 are the j = 1,

and 0 representations of su(2).

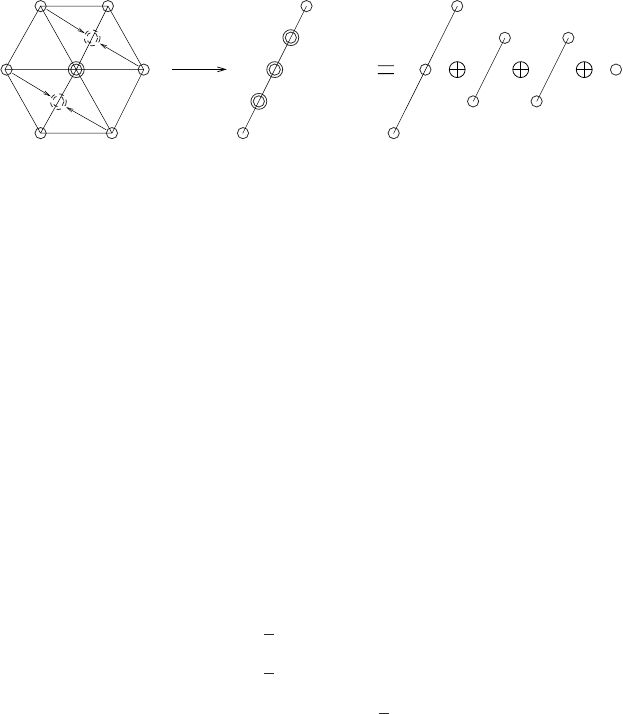
We can visualize this decomposition as coming about by first projecting the (λ

, λ

)

weights to the “m”ofthe|j, m labelling of su(2) as

m =

√

, (15.141)

15.3 Lie algebras 571

= 1

= 1/2

= 0

= 1/2

= 1

Figure 15.8 Projection of the su(3) weights on to su(2), and the decomposition

8 = 3 ⊕ 2 ⊕ 2 ⊕ 1.

and then stripping off the su(2) irreps as we did when decomposing product representions

(see Figure 15.8).

This branching pattern occurs in the strong interactions, where the mass of the strange

quark s being much larger than that of the light quarks u and d causes the octet of pseudo-

scalar mesons, which would all have the same mass if SU(3) flavour symmetry were

exact, to decompose into the triplet of pions π

, π

and π

−

, the pair K

and K

, their

antiparticles K

−

and

, and the singlet η.

There are obviously other su(2) subalgebras consisting of {T

, h

} and {U

, h

each giving rise to similar decompositions. These subalgebras, and a continuous infinity

of related ones, are obtained from the {V

, h

} algebra by conjugation by elements

of SU(3).

Another, unrelated, su(2) subalgebra consists of

√

2(U

+ T

−

√

2(U

−

+ T

−

* 2h

= (

√

3

). (15.142)

The factor of two between the assignment σ

* h

of our previous example and the

present assignment σ

* 2h

has a non-trivial effect on the branching rules. Under

restriction to this new subalgebra, the 8 of su(3) decomposes as

8 = 5 ⊕ 3, (15.143)

where the 5 and 3 are the j = 2 and j = 1 representations of su(2); see Figure 15.9.

A clue to the origin and significance of this subalgebra is found by noting that the 3

and

3 representations of su(3) both remain irreducible, but project to the same j = 1

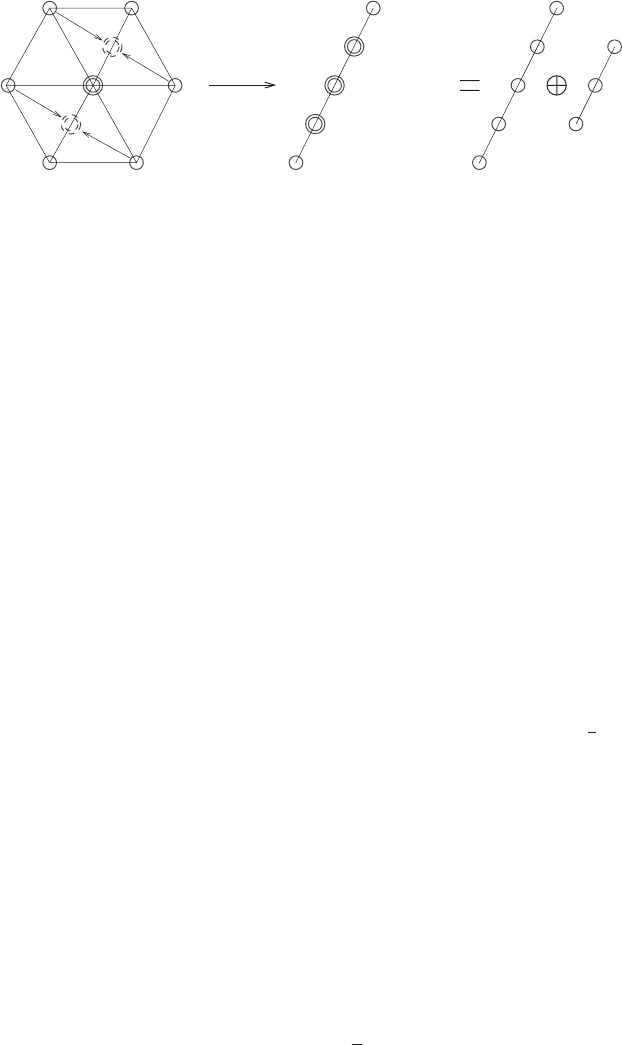
572 15 Lie groups

m = 2

m = 1

m = 0

m = 1

m = 2

Figure 15.9 The projection and decomposition for 8 = 5 ⊕ 3.

representation of su(2). Interpreting this j = 1 representation as the defining vector

representation of so(3) suggests (correctly) that our new su(2) subalgebra is the Lie

algebra of the SO(3) subgroup of SU(3) consisting of SU(3) matrices with real entries.

15.4 Further exercises and problems

Exercise 15.25: A Lie group manifold G has the property that it is parallelizable. This

term means that we can find a globally smooth basis for the tangent spaces. We can,

for example, take the basis vectors to be the left-invariant fields L

. The existence of a

positive-definite Killing metric also makes a compact Lie group into a Riemann manifold.

In the basis formed from the L

, the metric tensor g

=L

, L

 is then numerically

constant.

We may use the globally defined L

basis to define a connection and covariant deriva-

tive by setting ∇

= 0. When we do this, the connection components ω

are all zero,

as are all components of the Riemann curvature tensor. The connection is therefore flat.

The individual vectors composing a vector field with position-independent components

are therefore, by definition, parallel to each other.

(a) Show that this flat connection is compatible with the metric, but is not torsion free.

(b) Define a new connection and covariant derivative by setting ∇

, L

Show that this new connection remains compatible with the metric but is now torsion

free. It is therefore the Riemann connection. Compute components ω

of the new

connection in terms of the structure constants defined by [L

, L

]=−f

. Similarly

compute the components of the Riemann curvature tensor.

, the parametrized curves g(t) = Exp(tα

)g(0) are

geodesics of the Riemann metric.

Exercise 15.26: Campbell–Baker–Hausdorff formulæ. Here are some useful formula

for working with exponentials of matrices that do not commute with each other.

(a) Let X and Y be matrices. Show that

−tX

= Y + t[X , Y ]+

[X , [X , Y ]]+···,

the terms on the right being the series expansion of exp[ad(tX )]Y .

15.4 Further exercises and problems 573

(b) Let X and δX be matrices. Show that

−X

X +δX

= 1 +



−tX

δXe

dt + O

(δX )

= 1 + δX −

[X , δX ]+

[X , [X , δX ]]+···+O

(δX )

= 1 +



1 − e

−ad(X )

ad(X )



δX + O

(δX )

. (15.144)

= e

X +Y +

[X ,Y ]+higher

where “higher” means terms of higher order in X , Y . The next two terms are, in fact,

[X , [X , Y ]] +

[Y , [Y , X ]]. You will find the general formula in part (d).

(d) By using the formula from part (b), show that that e

can be written as e

, where

Z = X +



g(e

ad(X )

ad(tY )

)Ydt.

Here,

g(z) ≡

ln z

1 − 1/z

has a power-series expansion

g(z) = 1 +

(z − 1) +

(z − 1)

+···,

which is convergent for |z| < 1. Show that g(e

ad(X )

ad(tY )

) can be expanded as a

double power series in ad(X ) and ad(tY ), provided X and Y are small enough. This

ad(X ),ad(tY ) expansion allows us to evaluate the product of two matrix exponentials

as a third matrix exponential provided we know their commutator algebra.

Exercise 15.27:SU(2) disentangling theorems: Almost any 2×2 matrix can be factored

(a Gaussian decomposition) as







1 α



λ 0

0 µ



β 1



Use this trick to work the following problems:

(a) Show that

exp



iφ

=σ

− e

−iφ

=σ

−

)



= exp(α=σ

) exp(λ=σ

) exp(β=σ

−

574 15 Lie groups

where =σ

= (=σ

± i=σ

)/2, and

α = e

iφ

tan θ/2,

λ =−ln cos θ/2,

β =−e

−iφ

tan θ/2.

(b) Use the fact that the spin-

representation of SU(2) is faithful, to show that

exp



iφ

− e

−iφ

−

)



= exp(α

) exp(2λ

) exp(β

−

where

± i

. Take care, the reasoning here is subtle! Notice that the series

expansion of exponentials of =σ

truncates after the second term, but the same is not

true of the expansion of exponentials of the

. You need to explain why the formula

continues to hold in the absence of this truncation.

Exercise 15.28: Recall that the Lie algebra so(N ) of the group SO(N ) consists of the

skew-symmetric N -by-N matrices A with entries A

µν

=−A

νµ

. Let =γ

, µ = 1, ..., N

be the Dirac gamma matrices, and define



µν

to be the hermitian matrix

[=γ

, =γ

Construct the skew-hermitian matrix (A) from A by setting

(A) =



µν



µν

and similarly construct (B) and ([A, B]) from the skew-symmetric matrices B and

[A, B]. Show that

[(A), (B)]=([A, B]).

Conclude that the map A → (A) is a representation of so(N).

Exercise 15.29: Invariant tensors for SU(3). Let

be the Gell-Mann lambda matri-

ces. The totally anti-symmetric structure constants, f

ijk

, and a set of totally symmetric

constants, d

ijk

, are defined by

ijk

tr (

[

]), d

ijk

tr (

{

}).

In the second expression, the braces denote an anticommutator:

{x, y}

def

= xy + yx.

Let D

(g) be the matrices representing SU(3) in “8” – the eight-dimensional adjoint

representation.