Stevenson J. Power system analysis

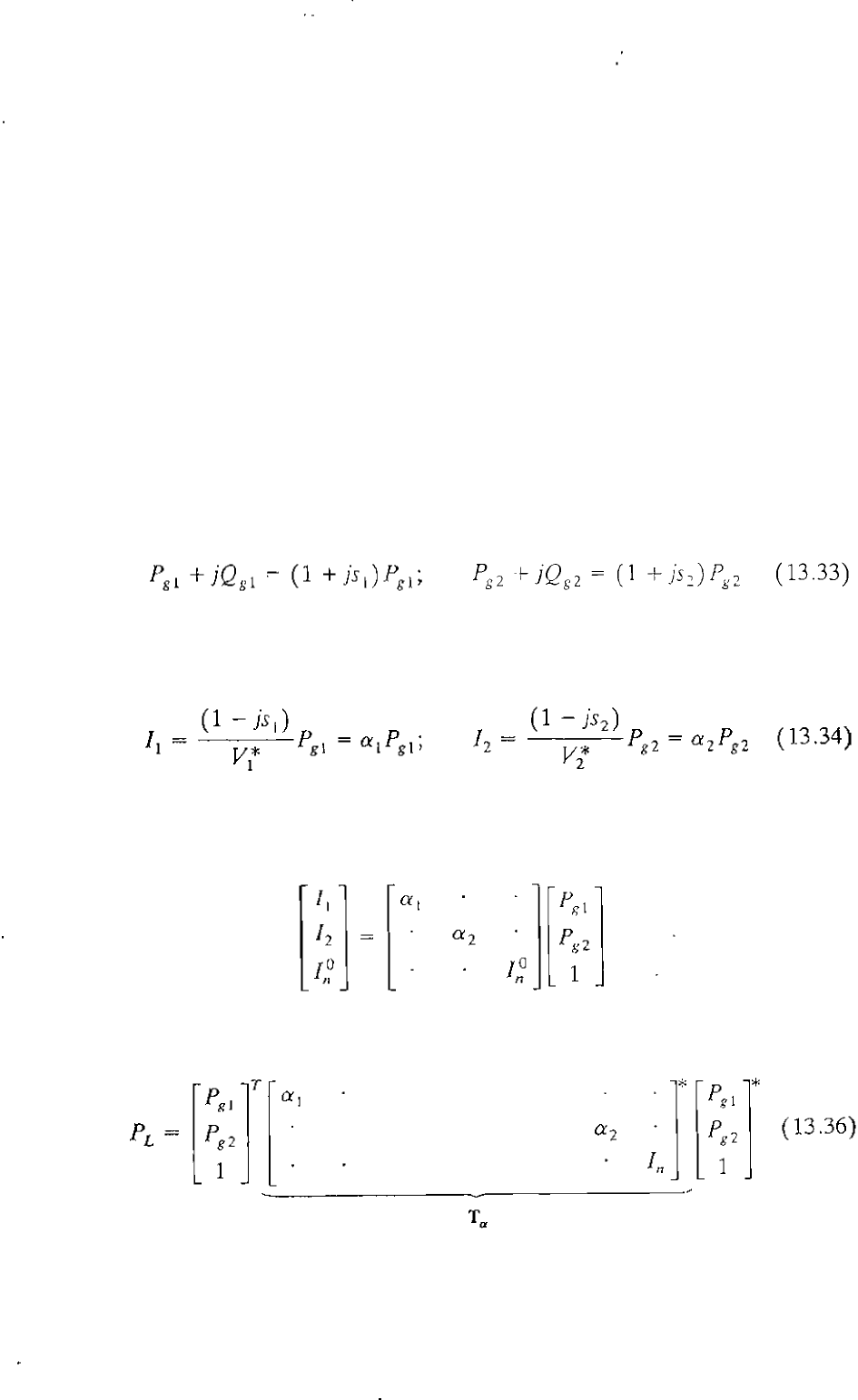
546

CHAPTER 13 ECONOMIC OPERATION OF POWER SYSTEMS

power loss of the system in terms of the generator currents 11 and 1

and the

no-load current I�. By xing upon bus



as the slack bus in power-ow

studies of the system, the current 1 �

1n/ Z 11 becomes a constant complex

number, which leaves 11 and 1

as the only variables in the loss expression of

Eq. (13.32).

Figure 13.5(b) helps to explain why I/� is called the no-load current. If all

load and generation were removed from the system and the voltage

were

applied at bus



, only the current l,�) would ow through the shunt connec

tions to node ®. This current is normally small and relatively constant since it

determined by Thcvenin i m pedance

' which includes the h igh impedances

of paths associated with line-charging and transformer magnetizing current but

not load.

At each generator bus we now assume th3t the reacti"e power QK

is a

constant fraction Si of the real power P

over the time period of interest. This

is equivalent to assuming that cach generator operates at a constant power

factor over the same period, and so we write

where

l/P

1 and S2

2/P

2 are real numbers. The output currents

from the genera tors are then given by

which al and a2 have obvious denitions. From Eqs. (13.34) the currents 11'

, and I� can be expressed in matrix form by

and substituting from this equation into Eq. (13.32), we obtain



: ]CIRbUSC* r�l

1°

(13.35)

We recall that the transpose of a product of matrices equals the reverse-order

product of their transposes. For instance, if there are three matrices A, B, and

C, we have (ABC)T

BTAT, and taking the complex conjugate of eacn side

.3 