Stevenson J. Power system analysis
Подождите немного. Документ загружается.

456
CHAPTER II SYMMETRICAL COMPONENTS AND SEQUENCE NETWORKS
z
+
GU
11.22
](0)
A
-
1-----
-
---'
I
N:
I _1
/30"
: 1 I
I
N
2
I
I
I
I
Ideal
I
__________ J
(b)
z
N
(a)
+
1
(0)
=
0
a
-
-----
-
----,
I
I
I
Nj
0
I
]
(
2
)
Z
IV3 -/-30 : 11
I N
2
1_
I
�1--�
a
1 t \ I :
t
+
Vf"
:
� � :
V(2)
_
_
___ -�r�i
_
�1
1
�
-�i--�!-
-
1
I
I
Ideal
I
, ___________ J
(c)
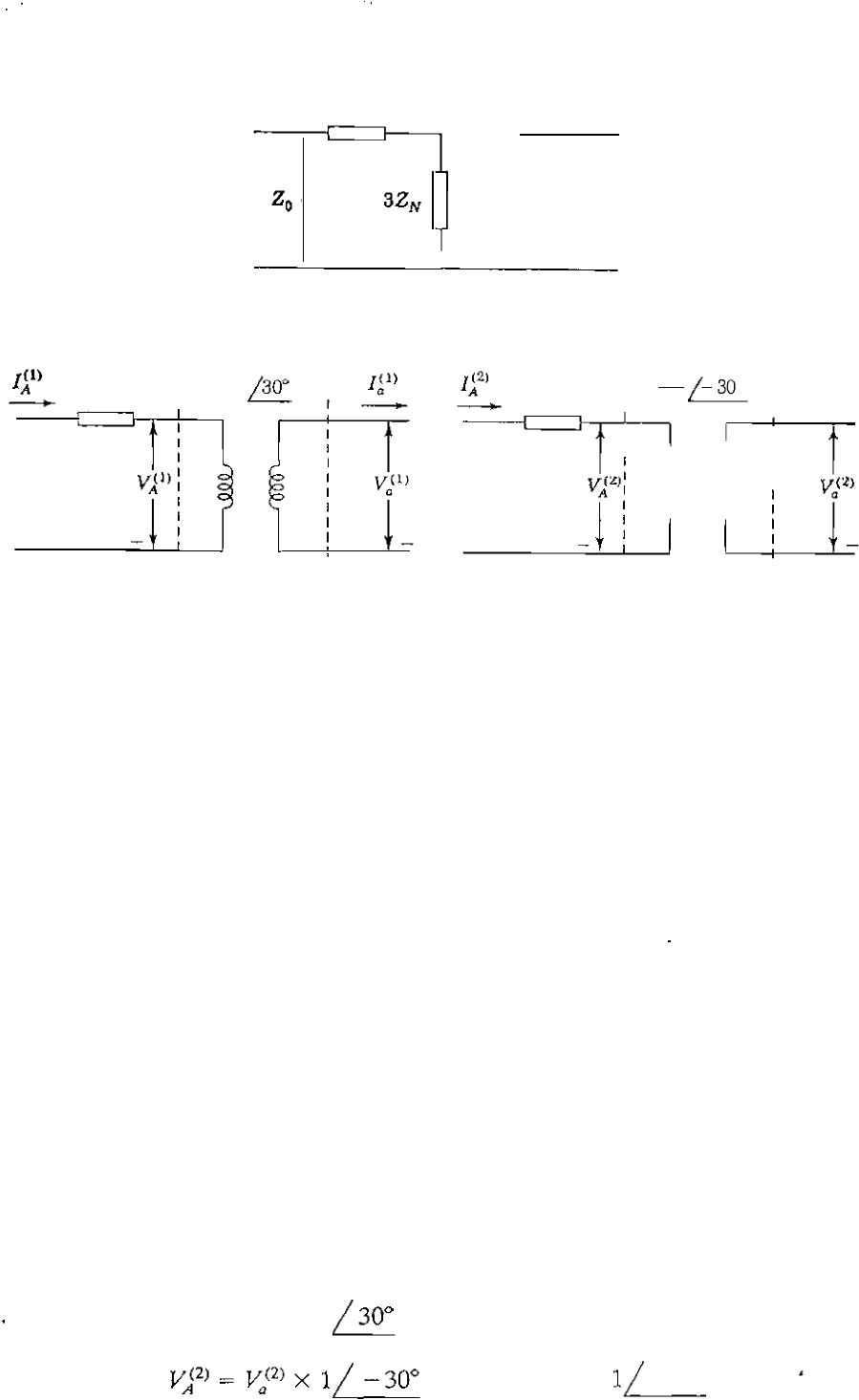
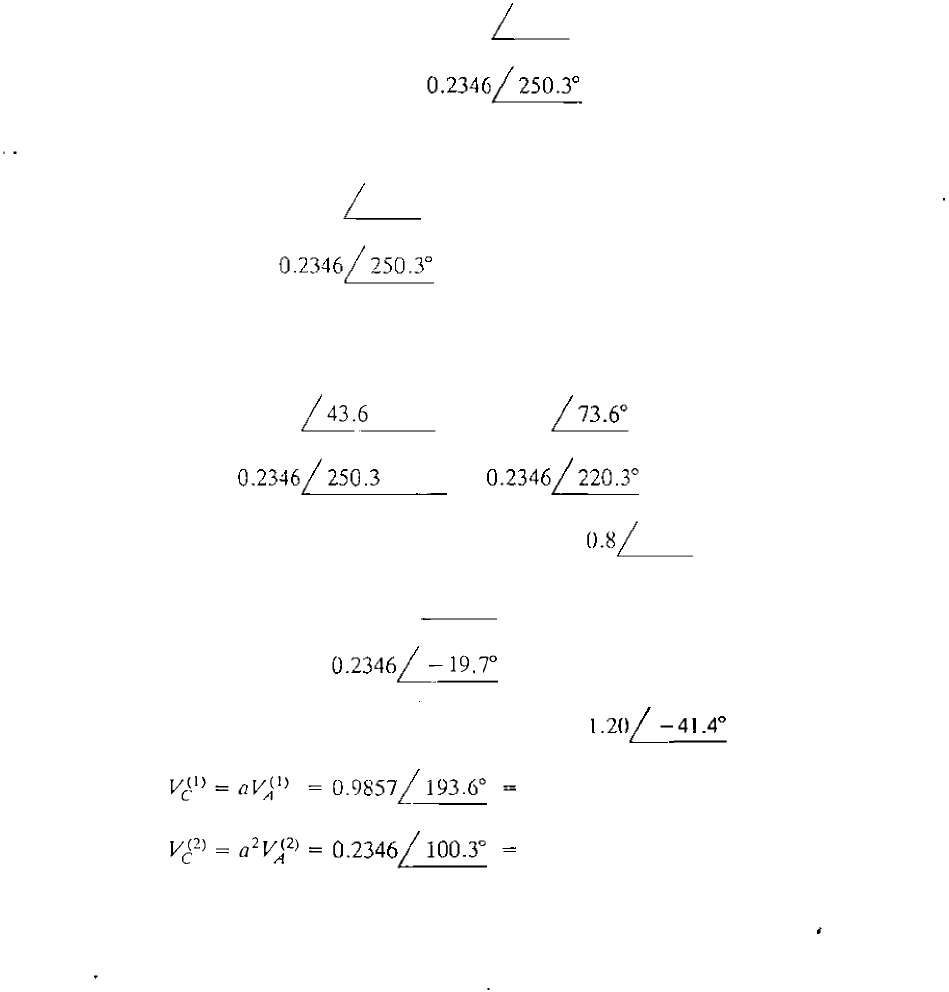
(a) The zero-sequence circuit of Y -� transformer bank with grounding impedance Z
N
and
corresponding (b) positive-sequence and (c) negative-sequence circuits.
the zero-sequence equivalent circuit must have impedance 3Z. in series with
the equivalent resistance and leakage reactance of the transformer to con
nect the line on the Y side to grou nu.
CASE 5. Y- Bank, Ungrounded Y
ungrounded Y is a special case where the impedance Z
N
between
neutral and ground is innite. The impedance 3Z
n
in the zero-sequence
equivalent circuit of Case 4 becomes innite and zero-sequence current cannot
ow in the transformer windings.
The positive- and negative-sequence equivalent circuits of the Y - trans
former shown in Figs. 11.22(b) and 1l.22(c) are based on Eqs. (11.87). We recall
from Sec. 2.6 that the multiplier Nil N
2
in Eqs. (11.87) is the ratio of the two
rated line-to-line (and also line-to-neutraU voltages of the Y- transformer. In
per-unit calculations, therefore, Eqs. (11.87) become exactly the same as Eqs.
(2.35), and again we have the rules
V(I) = V(
l
) X 1 /300
A
a
�
I�I) = I�!) X 1�
I�2) = I�
2
) X
1/
-300
( 11.88)
11.8 SEQUE
N
CE CIRCUITS OFY-ATRANSFORMERS
457
That is,
Wh
en stepping up from the low-voltage side to the high-voltage side of
a
�
-y or Y -
�
transformer, advance the positive-sequence voltages (and
currents) by 3
0
° and retard the negative-sequence voltages (and currents)
by 3
0
°.
The next example shows the numerical application of Eqs. (11 .88).
Example 11.7. The resistive Y -connected load bank of Example 11.2 is supplied
from the low-voltage Y-side of a Y- transformer. The voltages at the load are the
same as in that example. Find the line voltages and currents in per unit on the
high-voltage side of the transformer.
Sollliion. In Example 11.2 we fo und lhat the positive-and negative-sequence
currents owing toward the resistive load are
f,�')
=
0.9857
/
43.6° per u nit
I
(�)
=
0.2346/250.3° per unit
while the corresponding voltages on the low-voltage Y side of the transformer are
Va �) = 0.9857
/
43.6° per unit (
I
ine-to-neutral voltage base)
Va\� ) =
0.2346/250,3°
pe r unit (line-to-neutral voltage base)
Advancing the phase angle of the low-voltage positive-sequence voltage by 30° and
retarding the negative-sequence voltage by 30° give on the high-voltage side
Vj
I
) = 0.9857
�6
+
30° = 0.9857
/73.6°
= 0.2783 + }0.9456
vY ) =
0.2346/250.3
-30° =
0.2346
/
220.3°
= -0.1789 -}0.1517
V
A
= V�
I
) + vY ) =, 0.0994 + jO.7939 =
(/
82.80 per unit
V
JI)
=
a
VJ
I)
= 0.9857
!
-46.4
°
=
0.6798 -
}0.7138
Vf ) = vy)
=
O.2346-19.7°
= 0.2209 -}0.0791
VI I = V,�
I
) + v,F) = 0.9007 -jO.7929
=
1.2041.4° per unit
-0.9581 -}0.2318
-0.0419 + }0.2318
Vc = V�I) + VP ) = -1.0 +}O = 1.0� per unit

458
CHAER II SYMMETRICAL COMPONENTS AND SEOUENI: NETWORKS
Note that the line-ta-neutral voltages on the high-voltage side of the transformer
arc equal in per unit to the lillc-to-lillc voltages found in Example 11.2 for the
low-voltage Y side. The line-to-line voltages are
V
A
B = V
A
- VB = 0.0994 + jO.7939 -0.9007 + jO.7929 = -0.8013 + jl.5868
=
1.78/116.8"
p
er unit (line-neutral voltage base)
1.7S
/
I
=
- 2008 — 2025 «СтудМед»
