Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists

Подождите немного. Документ загружается.

brown : 25 colorless). Therefore the two categories of data are “brown” and

“colorless.”



ð75  75Þ

ð25  25Þ

¼ 0 þ 0 ¼ 0

The value of chi-square is zero when there is no diﬀerence between the

observed and expected values.

As the diﬀerence between the observed and expected values increases, so

does the value of chi-square. Here the observed ratio is 74 and 26. The value

of chi-square can only be a positive number because you always square the

diﬀerence between the observed and expected values.



ð74  75Þ

ð26  25Þ

¼ 0:0533

For an observed ratio of 70:30, the chi-square statistic is:



ð70  75Þ

ð30  25Þ

¼ 1:333

When you take samples from a population in a “category” experiment you

are, by chance, unlikely to always get perfect agreement to the ratio in the

population. For example, even when the ratio in the population is 75:25, some

samples will have that ratio, but you are also likely to get 76:24, 74:26, 77:23,

73:27 etc. The range of possible outcomes among 100 samples goes all the way

from 0:100 to 100:0. So the distribution of the chi-square statistic generated

by taking samples in two categories from a population in which there really is

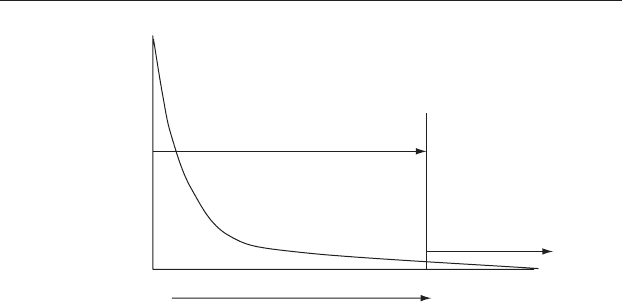
a ratio of 75:25 will look like the one in Figure 6.2, and the most unlikely 5% of

outcomes will generate values of the statistic that will be greater than a critical

value determined by the number of independent categories in the analysis.

Going back to the result of the gemstone treatment experiment given

above, the expected numbers are 75 and 25 and the observed numbers are

86 brown and 14 colorless.

To get the value of chi-square value, you calculate:



ð86  75Þ

ð14  25Þ

¼ 6:453

The critical 5% value of chi-square for an analysis of two independent

categories is 3.841. This means that only the most extreme 5% of departures

from the expected ratio will generate a chi-square statistic greater than this

6.8 Chi-square test for goodness of ﬁt63

value. There will be more about the chi-square test in Chapter 18, including

reference to a table of critical values in Appendix A.

Because the actual value of chi-square is 6.453, the observed result is

signiﬁcantly diﬀerent to the result expected under the null hypothesis. The

researcher would conclude that the ratio in the population sampled is not

3:1 and therefore reject the null hypothesis. It sounds like your new gem-

stone treatment is not as good as predicted (because only 14% were trans-

formed compared to the expected 25%), so you might have to revise your

estimated success rate of converting brown zircons into colorless ones.

6.9 What if you get a statistic with a probability

of exactly 0.05?

Many statistics texts do not mention this and students often ask “What if

you get a probability of exactly 0.05?” Here the result would be considered

not signiﬁcant since signiﬁcance has been deﬁned as a probability of less

than 0.05 (< 0.05). Some texts deﬁne a signiﬁcant result as one where the

probability is less than or equal to 0.05 (≤ 0.05). In practice this will make

very little diﬀerence, but since Fisher proposed the “less than 0.05” deﬁni-

tion, which is also used by most scientiﬁc publications, it will be used here.

Increasin

ositive value of chi-s

uare

Frequency

of these

outcomes

under the

null

hypothesis

95% of the values of the statistic

will be between zero and the 5%

critical value of chi-square

5% of the values

of the statistic will

exceed the

5% critical value

Figure 6.2 The distribution of the chi-square statistic generated by taking

samples from a population containing only two categories in a known ratio.

Many of the samples will have the same ratio as the expected and thus generate

a chi-square statistic of zero, but the remainder will diﬀer from this by chance,

thus giving positive values of chi-square. The most extreme 5% departures

from the expected ratio will generate statistics greater than the critical value of

chi-square.

64 Probability helps you make a decision about your results

More importantly, many researchers would be uneasy about any result

with a probability close to 0.05 and would be likely to repeat the experiment

because it is so close to the critical value. If the null hypothesis applies then

there is a 0.95 probability of a non-signiﬁcant result on any trial, so you

would be unlikely to get a similarly marginal result when you repeated the

experiment.

6.10 Conclusion

All statistical tests are a way of obtaining the probability of a particular

outcome. This probability is either generated directly as shown in the

“grains from a beach” example, or a test that generates a statistic (e.g. the

chi-square test) is applied to the data. A test statistic is just a number that

usually increases as the diﬀerence between an observed and expected value

(or between samples) also increases. As the value of the statistic becomes

larger and larger, the probability of an event generating that statistic gets

smaller and smaller. Once the probability of that event or one more extreme

is less than 5%, it is concluded that the outcome is statistically signiﬁcant.

A range of tests will be covered in the rest of this book, but most of them

are really just methods for obtaining the probability of an outcome that

helps you make a decision about your hypothesis. Nevertheless, it is impor-

tant to realize that the probability of the result does not make a decision for

you, and that even a statistically signiﬁcant result may not necessarily have

any geological signiﬁcance – the result has to be considered in relation to the

system you are investigating.

6.11 Questions

(1) Why would many scientists be uneasy about a probability of 0.06 for the

result of a statistical test?

(2) Deﬁne a Type 1 error and a Type 2 error.

(3) Discuss the use of the 0.05 signiﬁcance level in terms of assessing the

outcome of hypothesis testing. When might you use the 0.01 signiﬁ-

cance level instead?

6.11 Questions 65

7 Working from samples: data,

populations and statistics

7.1 Using a sample to infer the characteristics of a

population

Usually you cannot study the whole population, so every time you gather

data from a sample you are “working in the dark” because the sample may

not be very representative of that population. You have to take every possible

precaution, including having a good sampling design, to try to ensure a

representative sample. Unfortunately you still do not know whether it is

representative! Although it is dangerous to extrapolate to the more general

case from measurements on a subset of individuals, that is what researchers

have to do whenever they cannot work on the entire population.

This chapter discusses statistical methods for estimating the character-

istics of a population from a sample and explains how these estimates can be

used for signiﬁcance testing.

7.2 Statistical tests

Statistical tests can be divided into two groups, called parametric and non-

parametric tests. Parametric tests make certain assumptions, including that

the data ﬁt a known distribution. In most cases this is a normal distribution

(see below). These tests are used for ratio, interval or ordinal scale variables.

Non-parametric tests do not make so many assumptions. There is a wide

range of non-parametric tests available for ratio, interval, ordinal or nom-

inal scale variables.

7.3 The normal distribution

A lot of variables, including “geological” ones, tend to be normally distrib-

uted. For example, if you measure the slopes of the sides of 100 cinder cones

chosen at random and plot the frequency of these on the Y axis and angle on

the X axis, the distribution will look like a symmetrical bell, which has been

called the normal distribution (Figure 7.1).

The normal distribution has been found to apply to many types of

variables in natural phenomena (e.g. grain size distributions in rocks, the

shell length of many species of marine snails, stellar masses, the distribution

of minerals on beaches, etc.).

The very useful thing about normally distributed variables is that two

descriptive statistics – the mean and the standard deviation – can describe

this distribution. From these, you can predict the proportion of data that will

be less than or greater than a particular value. Consequently, tests that use the

properties of the normal distribution are straightforward, powerful and easy

to apply. To use them you have to be sure your data are reasonably “normal.”

(There are methods to assess normality and these will be described later.)

To understand parametric tests you need to be familiar with some

statistics used to describe the normal distribution and some of its properties.

7.3.1 The mean of a normally distributed population

First, the mean (the average) symbolized by the Greek μ describes the

location of the center of the normal distribution. It is the sum of all the

070average

Cinder cone an

le (°)

Frequency

of each

angle

Figure 7.1 An example of a normally distributed population. The shape of

the distribution is symmetrical about the average and the majority of values

are close to the average, with an upper and lower “tail” of steeply and gently

sloping cinder cones, respectively.

7.3 The normal distribution 67

values (X

, X

etc) divided by the population size (N). The formula for the

mean is:

 ¼

i¼1

(7:1)

This formula needs some explanation. It contains some common standard

abbreviations and symbols. First, the symbol Σ means “the sum of” and the

symbol X

means “All the X values speciﬁed by the restrictions listed below

and above the Σ symbol.” The lowest value of i is speciﬁed underneath Σ

(here it is 1, meaning the ﬁrst value in the data set for the population) and

the highest is speciﬁed above Σ (here it is N, which is the last value in the

data set for the population). The horizontal line means that the quantity

above this line is divided by the quantity below. Therefore, you add up all

the values (X

to X

) and then divide this number by the size of the

population (N).

(Some textbooks use Y instead of X. From Chapter 3 you will recall that

some data can be expressed as two-dimensional graphs with an X and Y

axis. Here we will use X and show distributions with a mean on the X axis,

but later in this book you will meet cases of data that can be thought of as

values of Y with distributions on the Y axis.)

As a quick example of the calculation of a mean, here is a population of

only four fossil snails (N = 4). The shell lengths in mm of these four individ-

uals (X

through to X

) are 6, 7, 9 and 10, so the mean, μ, is 32 ÷ 4 = 8 mm.

7.3.2 The variance of a population

The mean describes the location of the center of the normal distribution, but

two populations can have the same mean but very diﬀerent dispersions

around their means. For example, a population of four snail fossils with shell

lengths of 1, 2, 9 and 10 mm will have the same mean, but greater dispersion,

than another population of four with shell lengths of 5, 5, 6 and 6 mm.

There are several ways of indicating dispersion. The range, which is just

the diﬀerence between the lowest and highest value in the population, is

sometimes used. However, the variance, symbolized by the Greek σ

provides a lot of information about the normal distribution that can be

used in statistical tests.

68 Working from samples: data, populations and statistics

To calculate the variance, you ﬁrst calculate μ. Then, by subtraction, you

calculate the diﬀerence between each value (X

…X

) and μ, square these

diﬀerences (to convert each to a positive quantity) and add them together to

get the sum of the squares, which is then divided by the sample size. This is

similar to the way the average is calculated, but here you have an average

value for the dispersion.

This procedure is shown pictorially in Figure 7.2 for the population of

only four snail fossils, with shell lengths of 6, 7, 9 and 10 cm.

The formula for the above procedure is straightforward:



i¼1

ðX

Þ

(7:2)

If there is no dispersion at all, the variance will be zero (every value of X will

be the same and equal to μ, so the top line in the equation above will be

zero). The variance will increase as the dispersion of the values about the

mean increases.

(–1)

(–2) (+2)

67 9 10

µ = 8

(+1)

Differences squared: 4 1 1 4

Sum of the squared differences = 10

Population size = 4

Population variance = (10 ÷ 4) = 2.5

Figure 7.2 Calculation of the variance of a population consisting of only four

fossil snails with shell lengths of 6, 7, 9 and 10 mm, each indicated by the

symbol ■. The vertical line shows the mean μ. Horizontal arrows show the

diﬀerence between each value and the mean. The numbers in brackets are the

magnitude of each diﬀerence, and the contents of the box show these

diﬀerences squared, their sum and the variance obtained by dividing the sum

of the squared diﬀerences by the population size.

7.3 The normal distribution 69

7.3.3 The standard deviation of a population

The importance of the variance is apparent when you obtain the standard

deviation, which is symbolized for a population by σ and is just the square root

of the variance. For example, if the variance is 64, the standard deviation is 8.

The standard deviation is important because the mean of a normally

distributed population, plus or minus one standard deviation, includes

68.27% of the values within that population.

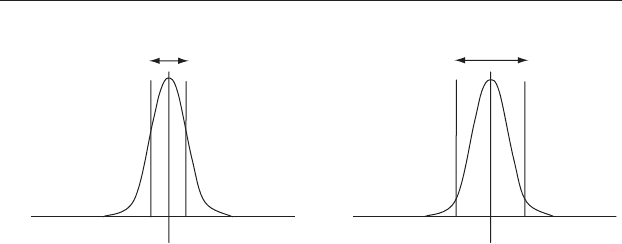
Even more importantly, 95% of the values in the population will be within

±1.96 standard deviations of the mean. This is especially useful because

the remaining 5% of values will be outside this range and therefore further

away from the mean (Figure 7.3). Remember from Chapter 6 that 5% is the

commonly used signiﬁcance level.

These two statistics are all you need to describe the location and shape of

a normal distribution and can also be used to determine the proportion

of the population that is less than or more than a particular value (Box 7.1).

7.3.4 The Z statistic

The proportions of the normal distribution described in the previous

section can be expressed in a diﬀerent and more workable way. For a normal

distribution, the diﬀerence between any value and the mean, divided by the

standard deviation, gives a ratio called the Z statistic that is also normally

Frequency

(a)

Frequency

(b)

Figure 7.3 Illustration of the proportions of the values in a normally

distributed population. (a) 68.27% of values are within ±1 standard deviation

from the mean and (b) 95% of values are within ±1.96 standard deviations

from the mean. These percentages correspond to the area of the distribution

enclosed by the two vertical lines.

70 Working from samples: data, populations and statistics

distributed, with a mean of zero and a standard deviation of 1.00. This

is called the standard normal distribution:

Z ¼

 



(7:3)

Consequently, the value of the Z statistic speciﬁes the number of standard

deviations it is from the mean. In the example in Box 7.1, a value of

189.6 μmis

1896 170

¼ 1:96 standard deviations away from the mean.

In contrast, a value of 175 μmis

175 170

¼ 0:5 standard deviations away

from the mean.

When this ratio is greater than +1.96 or less than −1.96, the probability of

obtaining that value of X is less than 5%. The Z statistic will be discussed

again later in this chapter.

7.4 Samples and populations

The equations for the mean, variance and standard deviation given above

apply to a population – the case where you have obtained data for every

case or individual that is present. For a population the values of μ, σ

and σ

are called parameters or population statistics and are true values (assum-

ing no mistakes in measurement or calculation). Of course in geological

situations we rarely have a true population, so μ and σ are not known and

must be estimated.

When you take a sample from a population and calculate the sample

mean, sample variance and sample standard deviation, these are true values

for that sample but are only estimates of μ, σ

and σ. Consequently, they are

given diﬀerent symbols (the Roman

X, s

and s respectively) and are called

sample statistics. But remember – because these statistics are only esti-

mates, they may not be accurate measures of the true population statistics.

Box 7.1 Use of the standard normal distribution

For a normally distributed population of plagioclase phenocrysts with a

mean length of 170 μm and a standard deviation of 10 μm, 95% of these

crystals will have lengths in the range from 170 ± (1.96 × 10) μm (which

is 150.4 to 189.6 μm). You only have a 5% chance of ﬁnding a phenocryst

that is either longer than 189.6 μ m or shorter than 150.4 μm.

7.4 Samples and populations 71

7.4.1 The sample mean

First, the procedure for calculating a sample mean is the same as for the

population mean, except (as mentioned above) the sample mean is sym-

bolized by

X because it is only an estimate of μ.

The sample mean is:

X ¼

i¼1

(7:4)

(Note that the lower case n is used to indicate the sample size, compared to

the capital N used to indicate the population size in Equation (7.1).)

7.4.2 The sample variance

When you calculate the sample variance, this estimate of σ

is also likely to

be subject to error. Small sample sizes introduce a consistent bias, but this

can be compensated for by a modiﬁcation to Equation (7.2). For a popula-

tion, the variance is:



i¼1

ðX

 Þ

(7:5 copied from 7:2)

In contrast, the sample variance is estimated using the following formula:

i¼1

ðX

 XÞ

n  1

(7:6)

Note that the sum of squares is divided by n – 1, but you would expect it

to be divided by n. This is to reduce a bias caused by the small sample size,

and it is easily explained by an example. Imagine you wanted to estimate the

population variance of the height of all adult Stegosaurus fossils from

the sample of the 80 that have been found. This small sample is unlikely

to include a suﬃcient proportion of animals that are in either the upper or

lower extremes of height within that population (the really short and really

tall animals), because there are relatively few of them. They will, never-

theless, make a big contribution to the population variance because they are

72 Working from samples: data, populations and statistics