Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists

Подождите немного. Документ загружается.

autocorrelation at low lags (Chapter 21), where values for points close to

each other within a sequence are more similar than those further apart. In

two dimensions, the space within which regional dependence occurs can be

visualized as a circle, with the amount of dependence decreasing with

distance outwards from the central point (Figure 22.9). This can be

extremely helpful in estimating the value of a variable at sites relatively

close to those where it is known.

22.4.1 The semivariance and semivariogram

A statistic that quantiﬁes the amount of regional dependence between two

points is the semivariance:

 ¼

ðX

 X

(22:16)

where X is the value of the variable at points X

and X

. For two identical

values the semivariance will be zero. As the diﬀerence between them

increases, so will the semivariance, which can only ever be zero or greater.

The semivariance is the same as the variance for a sample containing

only two points. For any sample from a population the variance is:

i¼1

ðX

 XÞ

n  1

(22:17 copied from 7:6)

For a sample of only two (X

and X

), the denominator (n − 1) is always

1.0, so Equation (22.17) for the variance becomes:

ðX

 XÞ

þðX

 XÞ

(22:18)

Figure 22.9 Illustration of regional dependence. The depth of shading

indicates the similarity between the value of a variable at the central point (X

)

decreasing with distance away from it (X

), until there is no dependence (X

22.4 Prediction and interpolation in two dimensions 353

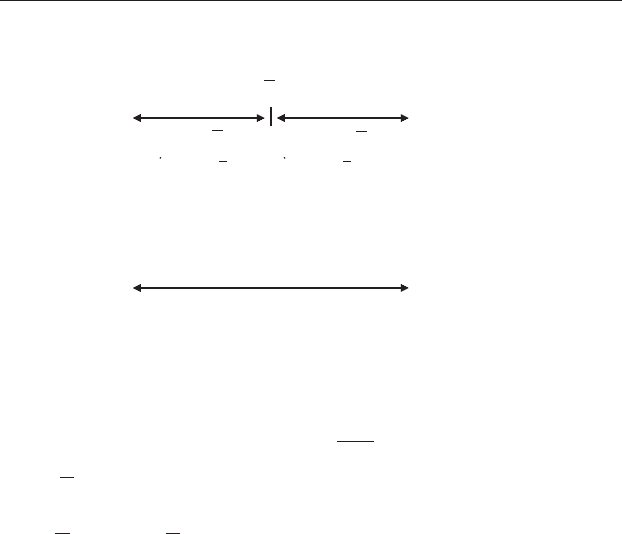
where X is the mean of the two values. This is the same as the semi-

variance (22.16), because the sum of the two squared diﬀerences

ðX

 XÞ

þðX

 XÞ

is mathematically equal to the diﬀerence between

the points squared and divided by two: ðX

 X

=2. A graphical explan-

ation of this equation is shown in Figure 22.10. If you were to take only two

points at random from a population, Equations (22.16) and (22.17) will

each estimate the population variance (but neither is likely to give an

accurate estimate because the sample size is only two).

The importance of the semivariance is its use as an accurate and precise

statistic to quantify the dissimilarity of a variable between a speciﬁcally

chosen central point (X

) and each of several other points (X

, X

, etc.)

increasingly distant from it. For each pair of points ((X

), (X

), etc.),

the value of the semivariance is plotted on the Y axis against the distance

between them on the X axis, to give a scatter plot called the experimental

(or sometimes the empirical) semivariogram. The relationship between the

semivariance and distance from the central point will depend on the

amount of regional dependence.

If there is no regional dependence, then the value of the variable at the

central point will be unrelated to its value elsewhere. So the scatter plot of the

semivariance will simply display a range of values, each of which is an estimate

of the population variance from a sample where n =2(Figure 22.11(a)).

(a) Variance from a sample of two points only = (3

+ 3

) ÷ 1 = 18

(distance a = 3)

(distance a + distance b = 6)

(distance b = 3)

(b) Semivariance = (6

) ÷ 2 = 18

= 7

= 13

= 7

– X)

– X

)

– X)

X =10

Figure 22.10 Graphical explanation of why the variance for a sample of two

points is the same as the semivariance. (a) Each value is equidistant from the

mean and the variance is therefore (distance a)

+ (distance b)

. (b) This is the

same as the semivariance (distance a + distance b)

÷ 2 because

mathematically, if a ¼ b ; a

þ b

ðaþbÞ

354 Introductory concepts of spatial analysis

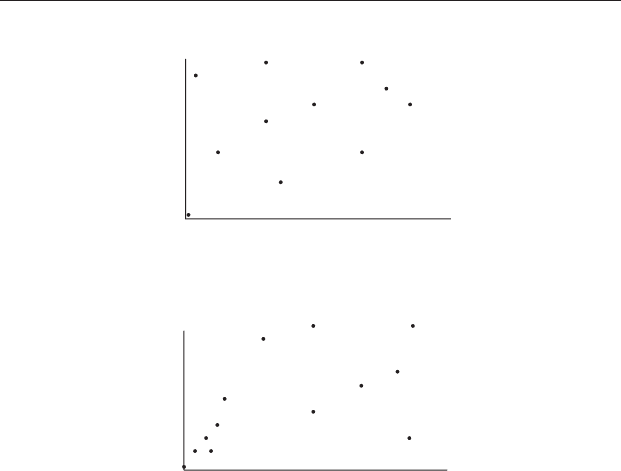
If there is some regional dependence, then the values of the variable at

the central point and those nearby will be similar, thereby giving relatively

small semivariances. As the distance from the central point increases, the

amount of dependence reduces, so the semivariances will tend to increase

but also become more scattered (Figure 22.11(b)). At this distance (and

beyond), the two points are equivalent to having been chosen at random

from the population, so each of the widely scattered semivariances will

estimate the population variance for samples of n =2.

Once the experimental semivariogram has been plotted, a smoothed line

of best ﬁt called the theoretical semivariogram is ﬁtted through the points

with the restriction that it must start from a relatively low value at the

central point, subsequently increase, but eventually plateau out. Theoretical

semivariograms have been ﬁtted to the two scatter plots in Figure 22.12.

When there is no regional dependence, the theoretical semivariogram

will rise extremely rapidly to a plateau that is equal to the population

(a)

Distance between sam

lin

oints

Semivariance

(b)

Distance between sam

lin

oints

Semivariance

Figure 22.11 The experimental semivariogram is a scatter plot of the

semivariance against distance between sampling points, where X = 0 is the

central location. (a) No regional dependence. (b) Strong regional dependence,

shown by the small semivariances between the central location and those

nearby.

22.4 Prediction and interpolation in two dimensions 355

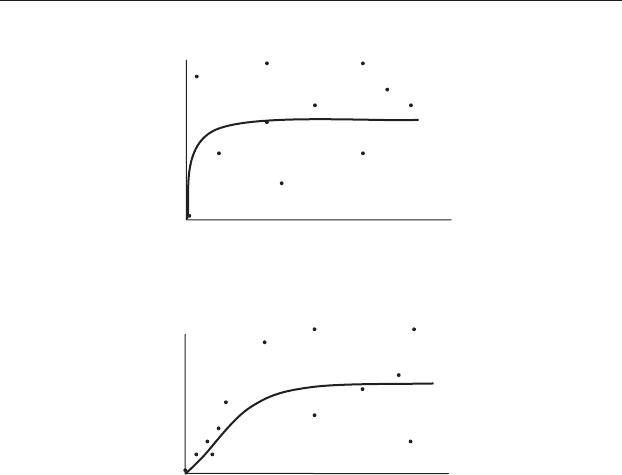
variance (Figure 22.12(a)). It will be a relatively good estimate of this para-

meter because it is the average of several semivariances scattered around it.

When there is regional dependence , the theoretical semivariogram will

initially have a low value near the central point, subsequently increase, but

eventually plateau out when the central point and those more distant from it

are no longer related. Here too, the averaged value at the plateau gives a

relatively good estimate of the population variance.

It may seem logical that the semivariance for two replicates taken at the

central location (and therefore “no distance” apart) should be zero

(e.g. Figure 22.12). However, this does not necessarily occur because there

may be within-site variation (which is the same as the “error” discussed in

Chapter 10) on an extremely small spatial scale that will give a relatively

small minimum semivariance (Figure 22.13).

The features of the theoretical semivariogram are shown in Figure 22.14.

The semivariance at X ¼ 0iscalledthenugget or nugget eﬀect.Whenthe

(a)

Distance between sam

lin

oints

Semivariance

(b)

Distance between sam

lin

oints

Semivariance

Figure 22.12 The theoretical semivariogram is a smoothed line ﬁtted to the

scatter plot of the semivariances against distance between sampling points,

where X = 0 is the central location. (a) No regional dependence. (b) Strong

regional dependence.

356 Introductory concepts of spatial analysis

semivariance reaches its maximum height at the plateau, its value is called the

sill. The outer limit of the region of inﬂuence surrounding the central point

is deﬁned as the value of X when the semivariance has reached 95% of the

diﬀerence between the sill and the nugget. For example, the distance

between a nugget of 40 and a sill of 200 is 160, so the value of the semivariance

at the outer limit of the region of inﬂuence is 40 + (0.95 × 160) = 192. The

region of inﬂuence can be estimated graphically by reverse prediction as

shown in Figure 22.14 and represents the distance outwards from the central

location within which the variable shows some regional dependence.

The theoretical semivariogram used to be ﬁtted by eye, but there are

several equations available to estimate it. One of the most commonly used is

the exponential:

Y ¼ c þðS cÞð1  e



Þ (22:19)

Distance between sam

lin

oints

Semivariance

Figure 22.13 Variation among replicates taken at the same location will give

a semivariance of more than zero at the central point.

Sill 200

Nugget

Distance between sam

lin

oints

Region

influence

Semivariance

Figure 22.14 Features of the theoretical semiovariogram. When X = 0 the

value of the semivariance is called the nugget. The maximum value (at the

plateau) is the sill. The region of inﬂuence is the value of X (estimated

graphically by reverse prediction) for which the theoretical semivariance is

95% of the distance between the sill and the nugget.

22.4 Prediction and interpolation in two dimensions 357

where Y is the semivariance, c is the nugget, S is the sill, e is the natural

logarithm, h is the distance from the central point and a is the range of

inﬂuence. This will always give a relationship that increases but eventually

plateaus out.

22.4.2 A worked example

Table 22.5 gives data for the depth, in meters, of a West Virginia coal deposit

at a central location and for 15 pits increasingly distant from it.

The semivariances were calculated using Equation (22.16). The experi-

mental semivariogram is shown in Figure 22.15 and suggests some regional

dependence because the semivariances between Pit 1 and each of Pits 2, 3 and

4 are relatively small. Simply by inspection, the theoretical semivariogram

has a nugget of zero, a sill of about 220 km, and a region of inﬂuence of about

25 km, with the last obtained by graphical reverse prediction from a semi-

variance of 0 + 0.95 × (220 – 0) (see above).

Table 22.5 Depth of a coal deposit, in meters, at a central point and 15

other pits at various distances from it. This is a case where the nugget is

zero.

Pit number

Depth of coal

bed (m) Semivariance

Distance from Pit

1 (km)

1 (central point) 11 0.0 0

2 12 0.5 1

3 11 0.0 3

4 14 4.5 4

5 34 264.5 14

6 4 24.5 20

7 42 480.0 28

8 32 220.5 32

9 17 18.0 40

10 28 144.5 54

11 34 265.5 67

12 25 98.0 70

13 37 338.0 76

14 41 450.0 79

15 7 8.0 100

16 29 162.0 125

358 Introductory concepts of spatial analysis

22.4.3 Application of the theoretical semivariogram

One important application of the theoretical semivariogram is to predict the

value of a variable at sites where it has not been measured. The width of the

95% conﬁdence interval around the line of the theoretical semivariogram

will depend on the amount of regional dependence. When there is no

regional dependence, the line will rise rapidly and the 95% conﬁdence

interval around it will be relatively wide, because it is the smoothed average

of many estimates made when n = 2. When there is regional dependence,

050

Distance in km from

it 1

(a)

Semivariance

100

200

400

600

050

Distance in km from

it 1

(b)

Semivariance

100

200

400

600

Figure 22.15 (a) Experimental semivariogram showing the semivariance

plotted against the distance in kilometers from the central point of Pit number

1. (b) Theoretical semivariogram for an exponential function ﬁtted to the same

data. The horizontal dashed line shows the sill. The vertical dashed line shows

the region of in ﬂuence of about 25 km, estimated graphically from a

semivariance of 209 that was calculated as 95% of the diﬀerence between the

sill and the nugget.

22.4 Prediction and interpolation in two dimensions 359

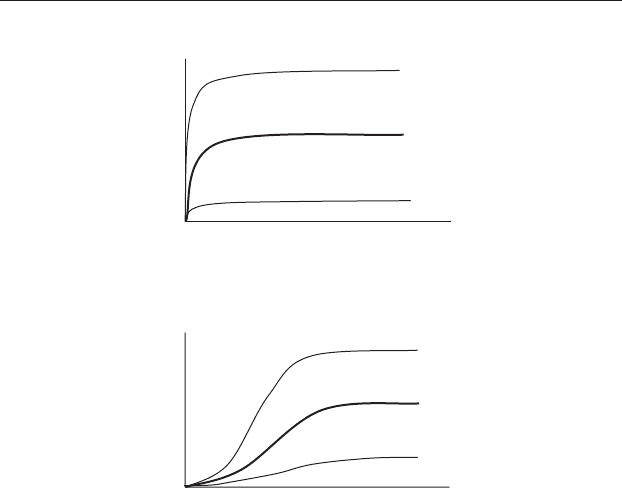
the line will rise more slowly. Its 95% conﬁdence interval will initially be

very narrow because the regional dependence surrounding the central point

will constrain the estimates of the semivariance to within a relatively small

range (Figure 22.16).

If a variable shows regional dependence and the point(s) at which you

want to predict it lie within the regions of inﬂuence of known locations, it is

possible to make quite precise estimates of its value. This is the basis of the

method of interpolation called Kriging (named after D. G. Krige who

developed the technique).

This is an extreme simpliﬁcation, but essentially Kriging gives the solution to

a set of simultaneous equations so that the value at an unknown site is the best

Distance between sam

lin

oints

(a)

Semivariance

Distance between sampling points

(b)

Semivariance

Figure 22.16 The 95% con ﬁdence limits (lighter lines) surrounding the line

for the theoretical semivariance (heavy line) will depend on the extent of

regional dependence. (a) No regional dependence will give a uniform

conﬁdence interval (and thus a very imprecise semivariance) for any point

outside the central one. (b) When there is regional dependence, the conﬁdence

interval will initially be narrow but will increase (thus initially showing high

precision, which will decrease with distance from the central point).

360 Introductory concepts of spatial analysis

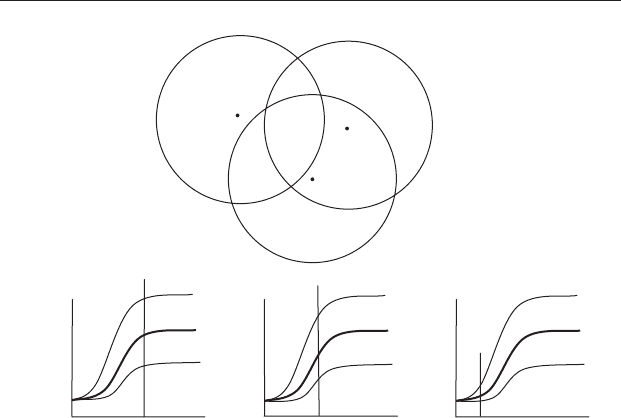
possible overall ﬁt to the appropriate points on the theoretical semivariograms

that overlap it. A graphical example to illustrate the concept is given in

Figure 22.17. The value of the variable is not known for point D, but D lies

within the regions of inﬂuence of points A, B and C where the variable is

known. Note that D is closest to the central region of C and therefore positioned

on the left-hand side of the theoretical semivariogram for C, where the semi-

variance is relatively low (Figure 22.17(c)). Consequently, C has the greatest

inﬂuence upon the estimate of the value of D, which must be close to the actual

value of C at the central point in order to ﬁt within the 95% conﬁdence interval

of the theoretical semivariogram. In contrast, B has less inﬂuence (Figure 22.17

(b))andAhastheleastinﬂuence on D (Figure 22.17(a)).

An enormous amount has been written (including many advanced text-

books) on Kriging, together with computer programs for carrying out the

AB C

(a) (b) (c)

Figure 22.17 The value of a variable is known for sites A, B and C, and needs

to be estimated for site D. The region of inﬂuence is shown as a circle around

each known site. Note that point D is near the edge of the region of inﬂuence

for A, closer to the central point of B, and very close to the central point of

C. The value of the variable estimated for D must be one that gives the best

possible ﬁt to its position on the three theoretical semivariograms (darker

lines), taking into account the 95% conﬁdence intervals (lighter lines), for A, B

and C.

22.4 Prediction and interpolation in two dimensions 361

complex calculations required. The detailed methods used for Kriging are

beyond the scope of this introductory text, but an excellent explanation is

given by Davis (2002).

22.5 Conclusion

This chapter is an introduction to some essential concepts of spatial analysis

that underpin many of the methods used by earth scientists. It is designed to

give an understanding of random and non-random spatial distributions,

and an introduction to the analysis of directional data and the concept of

estimation and interpolation using regional dependence. It will be partic-

ularly helpful in evaluating the conclusions in reports and from research

that uses these methods.

22.6 Questions

(1) The table below gives the observed number of silver mines in 200

quadrat samples, each 1 km

in area, in northern Idaho. The total

number of mines was 276 and the mean number per quadrat is 1.38.

Number of mines per quadrat Observed frequency of cases

044

187

231

327

8 and more 0

Total n = 200

Mean 1.38

(a) Calculate the expected proportion, and the expected frequency, of

quadrats containing zero, 1, 2, etc. mines if the distribution is random

and test the hypothesis that the observed distribution is random using the

methods in Section 22.2.1.Isthevalueofchi-squaresigniﬁcant? (b) What

362 Introductory concepts of spatial analysis