Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists

Подождите немного. Документ загружается.

Box 22.3 A Monte Carlo approach to assessing randomness: the

spatial distribution of impact craters on Venus

Another way of assessing a spatial pattern for randomness is to use the

Monte Carlo method (Chapter 18) to take a large number of simulated

random samples and create a distribution that would apply under the

null hypothesis.

Photographs from the Magellan mission show that the planet Venus

has relatively few impact craters and these appear to be randomly

distributed. The low number of craters suggests the surface is relatively

young, because craters accumulate over time: for example the Moon has

older terrain that is heavily cratered (like the light-colored highlands)

and younger terrain with signiﬁcantly fewer craters (like the basaltic

maria). The random distribution of craters suggests there is little or no

recent tectonic activity, because this will continually create patches of

new crust where there will initially be no craters, thereby giving a spatial

distribution of craters that is clustered rather than random. The hypoth-

esis that the surface of Venus is relatively young with little or no recent

tectonic activity was highly controversial. Strom et al.(1994) compared

the observed spatial distribution of impact craters on Venus with that

expected for a random distribution, using a Monte Carlo simulation, and

concluded that the distribution of craters was random. The implied lack

of recent tectonic activity on Venus is now widely accepted.

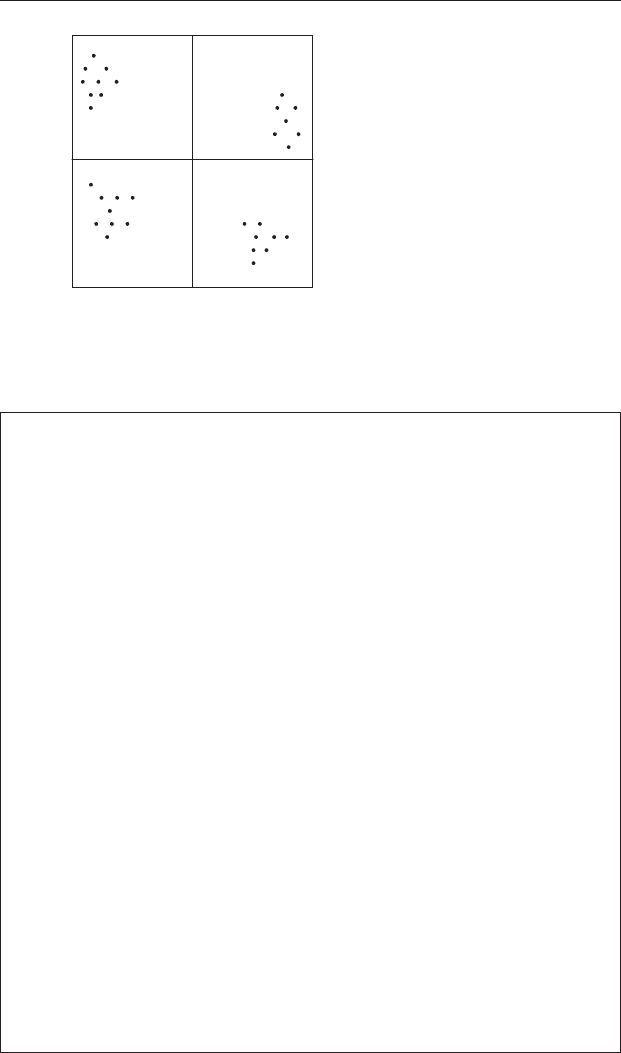
Figure 22.3 A relatively large quadrat size may not detect clustering on a

smaller scale. The number of points within each of the four quadrats is very

similar (thus suggesting an even distribution) despite extreme clustering.

22.2 Testing for randomness 343

incre ases, the average distance between each point and the one closest to it

(its nearest neighbor) will decrease. Here too, a formula derived from the

Poisson is used to predict the expected average distance between nearest

neighbors when the pattern is random:

d ¼

ﬃﬃﬃﬃ

(22:10)

where A is the area of the sampling space and n is the total number of points

within it.

This expected value can be compared to the observed mean distance

between nearest neighbors,



d, from the sample. The standard error of the

mean (SEM) of the nearest neighbor distances is:

SEM ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð4  pÞA

4pn

(22:11)

using the constant p (3.147) and A and n as in the previous equation.

The Z test is used to compare

d and d:

Z ¼

d  d

SEM

(22:12)

Once Z is outside the range of ±1.96, the mean distance between nearest

neighbors is signiﬁcantly diﬀerent than that expected if the points are

distributed at random.

Although nearest neighbor analysis is not aﬀected by scale, it is sensitive

to edge eﬀects that occur because points close to the edge of the sampling

space can only have neighbors within it. If the space were larger, the points

might have closer nearest neighbors (Figure 22.4).

One solution to this bias is to designate a strip around the outer edge of

the sampling space as a guard region and only measure the nearest neigh-

bor distances from each of the points within the remaining (reduced) area

in the middle (Figure 22.5). Some of the nearest neighbors of these points

may be in the guard region, and the distances measured out to them will be

realistic if the guard region is wide enough. Unfortunately, however, using

part of the sample space as a guard region reduces the sample size.

Another method is to create an artiﬁcial guard region by making eight

copies of the sampling space and placing these around the original, as shown

in Figure 22.6. Here too, the nearest neighbor distances are only measured

344 Introductory concepts of spatial analysis

from points within the original sampling space. This method does not

reduce the sample size.

22.2.4 A worked example

Table 22.2 gives the nearest neighbor distances for the 17 points within the

35 × 43 km central region shown in Figure 22.5. Points have been numbered

in order, running across and down from the top left-hand corner. It is

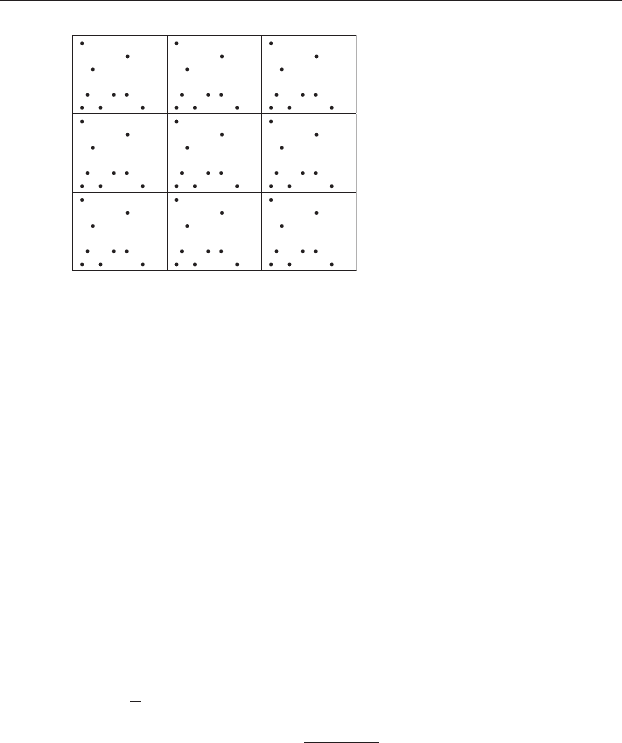
Figure 22.5 Use of a guard region to reduce edge eﬀects. Nearest neighbor

distances are only measured from points within the central (and therefore

reduced) sampling space. Some nearest neighbors to these points may be

within the guard region, and the distances to them will be representative

provided the guard region is wide enough.

Figure 22.4 Nearest neighbor analysis can be subject to edge eﬀects. Some of

the points within the sampling space have “true” nearest neighbors that are

outside the boundary, but their nearest neighbors within the sampling space

are further away. Restricting the measurements to nearest neighbors within

the sampling space will overestimate the mean nearest neighbor distance.

22.2 Testing for randomness 345

important to note that the nearest neighbor distance is measured from every

point within the sampling space. Therefore, for two points designated as “a”

and “b” that are each other’s nearest neighbors within the central region

(e.g. points 1 and 2 just inside the top left-hand corner of the central region

of Figure 22.7), the distance from point a to its nearest neighbor point b is

2.7 km, but so is the distance from point b to its nearest neighbor, which in

this case is point a. For n points there have to be n distances, so the same

distance is recorded for each of these two points.

The area of the central region is 35 × 43 = 1505 km

. There are 17 points,

so the expected average distance between nearest neighbors (Equation

(22.10)) is 4.705 km, with an SEM of 0.596 (Equation (22.11)). The observed

mean distance,

d, from Table 22.2 is 4.662.

The Z score (Equation (22.12)) is:

4:6624:705

0:596

¼0:072. This is within the

range of ±1.96, so the mean nearest neighbor distance is no di ﬀ erent to that

expected if the distribution is random.

22.3 Data for the direction of objects

An object with a reco gniz able direction that has a “head and a tail” (i.e. it

represents an arrow rather than a line) within a two-dimensional (or

higher) sampling space will face in a particular direction.Fortwodimen-

sions, this can be qu antiﬁed by a single number in relation to a reference

(e.g. true Nor th, the true vertical or some de ﬁned direction) in degrees of a

circle from 1° to 360°. Summary statistics for directional data have many

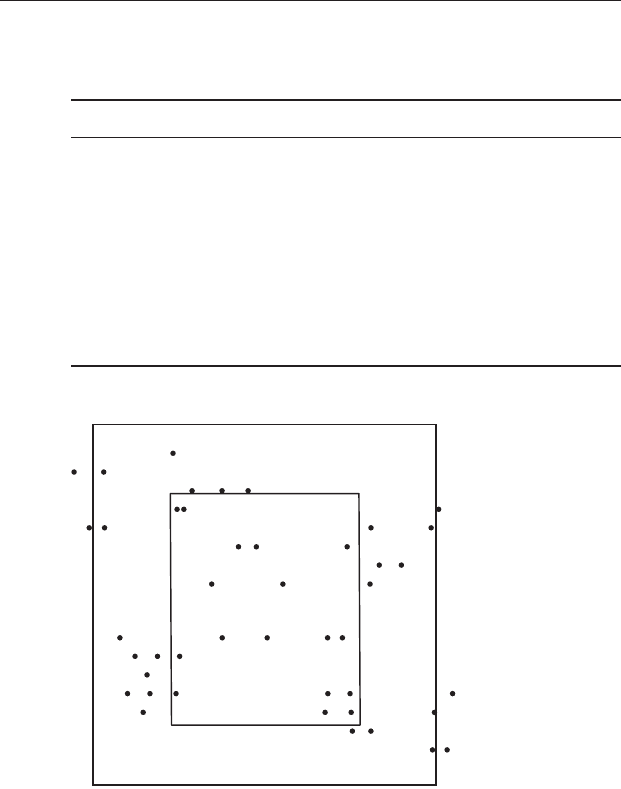
Figure 22.6 Use of an artiﬁcial guard region for nearest neighbor analysis.

The original sample space (center square) has been copied eight times, and the

copies placed in the same orientation around it. Nearest neighbor distances are

only measured from points within the central sampling space.

346 Introductory concepts of spatial analysis

applications. For example, the directions of streams in a ﬂoodplain can be

used to model the eﬀects of rainfall upon a catchment and historical data

for the directions moved by cyclones and hurricanes can be used to predict

their paths.

Table 22.2 The distances, in kilometers, to their nearest neighbor, for the

17 numbered points within the central area of Figure 22.7.

Point number Distance Point number Distance

1 1.65 10 2.70

2 1.65 11 2.70

3 3.40 12 3.95

4 3.40 13 4.75

5 5.90 14 4.25

6 8.30 15 3.90

7 8.30 16 3.90

8 8.30 17 3.90

9 8.30 Average: 4.662

1,2

34 5

14 15

1716

10 11

Figure 22.7 For the 17 points (numbered in order running across and down

from the top left-hand corner within the central region of the sampling space),

the nearest neighbor distances for points 1 and 2 are the same, because each is

the other’s nearest neighbor. The same applies to points 3 and 4; 10 and 11; 15

and 17. The nearest neighbors of points 5, 12 and 13 are in the guard region.

The central area is 35 × 43 km.

22.3 Data for the direction of objects 347

22.3.1 Summarizing and displaying directional data

If you have data for the wind or water ﬂow directions at several diﬀerent

locations, they can be summarized and displayed by an extension of the

method used to generate a histogram (Chapter 3 and Section 22.2). For each

location, the direction is recorded in degrees, from one to 360°. Next the

circle is subdivided into several equal arcs (e.g. 1–90°, 91–180°, 181–270°

and 271–360°), and the number of cases within each is counted to give a

table of frequencies. These divisions are often called bins. The summary

data could be displayed as a conventional histogram (Chapter 3), but to

show the actual or relative directions of the objects they are usually plotted

in a circular histogram, which is a circle divided into several equal arcs,

equivalent to the bars of a conventional histogram, with the radius of the

ﬁlled area indicating the frequency within each bin. This is called a rose

diagram because a circle subdivided into ﬁlled arcs of diﬀerent radii some-

what resembles a ﬂower. Two examples are shown in Figure 22.8. Here, just

as for a conventional histogram, the number of bins and their ‘width’ in

degrees must be chosen to give a meaningful display (Chapter 3).

Rose diagrams can be visually misleading, because the width and area of

an arc increase with distance from the origin. Therefore, if only the petal

length is proportional to the frequency of cases within each arc, the

perceived importance of relatively low counts will be reduced and that of

relatively high ones increased (Figure 22.8(a)). For this reason, rose dia-

grams are usually plotted with the area of each petal being proportional to

the frequency of cases (Figure 22.8(b)).

22.3.2 Drawing a rose diagram

The following method gives a rose diagram where the largest frequency

always extends to the maximum radius of the rose. For example, for a rose

diagram of radius 24 mm, the angular division containing the largest count

will have this petal length.

To draw a rose diagram where the length of each petal is proportional

to its frequency, the number of cases within each bin is counted from the

raw data. Petal lengths are calculated using the formula:

petal length ¼

max

 Freq

pet

Freq

max

(22:13)

348 Introductory concepts of spatial analysis

where r

max

is the maximum radius of the rose diagram, Freq

pet

is the

frequency for a particular petal and Freq

max

is the highest frequency within

the set of petals. Therefore, for the highest frequency, Freq

pet

will be equal to

Freq

max

so its petal length will be r

max

. There is worked example in

Section 22.3.3.

To draw a rose diagram where the area of each petal is proportional to

its frequency, the procedure described above is followed, except that petal

(a)

(b)

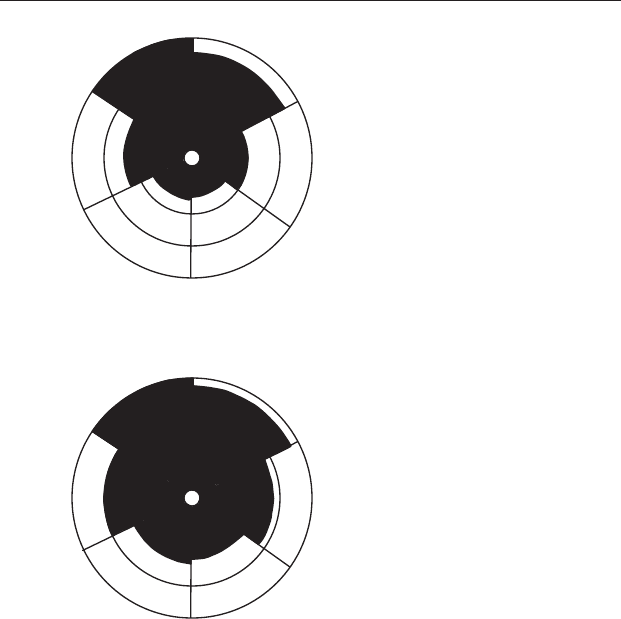
Figure 22.8 Rose diagrams from the data in Table 22.3. (a) Petal length is

directly proportional to the frequency within each angular division. (b) Petal

length when petal area is directly proportional to the frequency within each

division. Note that (a) gives the visual impression of a far less symmetrical

distribution.

22.3 Data for the direction of objects 349

length is calculated using the formula:

petal length ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

max

 Freq

pet

Freq

max

(22:14)

where r

max

is the square of the maximum radius of the rose diagram. Here

too, when Freq

pet

is equal to Freq

max

, the petal length will be r

max

. There is a

worked example below.

22.3.3 Worked examples of rose diagrams

Data for the directions of 250 streams in the Channel country of western

Queensland, as summarized for six equal angular divisions of 60°, are given in

Table 22.3. These have been used to calculate petal length when it is directly

proportional to frequency (Equation (22.13)), and petal length when the petal

area is directly proportional to frequency (Equation (22.14)). The two rose

diagrams are shown in Figure 22.8. By inspection, the diagram where petal

length is proportional to frequency gives the misleading perception that a

greater proportion of the objects face towards the upper part of the rose than

does the one where petal area is proportional to frequency. When interpreting

rose diagrams, it is important to know which scale has been used! It is not

Table 22.3 Summary data for the direction, in degrees, of 250 streams in the

Channel country of western Queensland. The maximum observed frequency is 73

and the maximum radius of the rose diagram has been chosen as 24 mm. (a) Petal

lengths that are directly proportional to frequency. (b) Petal lengths, when petal area

is directly proportional to frequency.

Direction

Observed

frequency

(a) Petal length (mm) when

proportional to frequency

(b) Petal length (mm) when

petal area is proportional to

frequency

1–60 63 20.7 22.3

61–120 31 10.2 15.6

121–180 20 6.6 12.6

181–240 22 7.2 13.2

241–300 41 13.5 18.0

301–360 73 24.0 24.0

Total 250

350 Introductory concepts of spatial analysis

unknown for mining companies to produce prospectuses containing mislead-

ing rose diagrams. The use of the “area proportional” type is recommended.

22.3.4 Testing whether directional data show a pattern

There are numerous tests for whether the directions faced by a sample of

objects shows a relatively even angular distribution or some pattern. If all

directions are equally likely, then the expected number of observations

within each equal subdivision should, on average, be the same, and the

rose diagram will be symmetrical. This hypothesis can be tested by a chi-

square goodness of ﬁt between the observed and expected frequencies:



i¼1

ðo

 e

(22:15 copied from 18:1)

The number of degrees of freedom is one less than the number of bins

(see Box 22.2).

22.3.5 A worked example

Table 22.4 gives summary data for the direction, in degrees, for the sample

of 250 streams in Table 22.3, together with the expected frequency when

there are equal numbers in every bin. The chi-square goodness of ﬁt test is

signiﬁcant: 

¼ 57:77, so P < 0.001, indicating that the orientation of the

valleys is not equally likely in all directions. By inspection, it appears that

most are facing from the north-west through to the north-east (301°

through 0° to 60°).

22.3.6 Data for the orientation of objects

Objects without a deﬁnable “head or tail” (e.g. where the object being mapped

is a line or a plane) cannot be assigned a speciﬁc direction in a two-

dimensional space. They face in two directions, which for a straight object

(such as the strike of contacts between overlying formations) will be 180°

apart (e.g. 24° and 204°). Instead, data for the orientations of these objects are

often given as two directions and both are recorded in the table of frequencies

used to draw a rose diagram (Section 22.3.2). For straight objects, the rose

diagram showing orientation will always be perfectly symmetrical, with petals

22.3 Data for the direction of objects 351

of identical length occurring opposite to each other. Caution is needed when

using these data to test hypotheses about whether objects are orientated at

random because the table of frequencies will contain 2n data from n objects

and therefore inﬂate the value of a statistic such as chi-square. One solution

for straight objects is simply to double all the angles (Krumbein, 1939). For a

circle subdivided into 360°, this always gives the same angle for both direc-

tions (e.g. an object orientated at 30° and 210° will have doubled angles of 60°

and 420°, the latter of which is 360° + 60° and thus equal to 60°). So you need

to record the value of the doubled angle only once in a table of frequencies

used for a chi-square test for randomness (Section 22.3.5).

22.4 Prediction and interpolation in two dimensions

Often data are obtained for a ratio or interval scale variable that is measured

at several locations, but there is a need to predict its value elsewhere within

the same sampling space. For example, you might have data for the per-

centage of nickel at ten locations within a mining lease and want to predict

the areas where additional exploration is likely to discover high yielding

deposits within that lease.

One very important property of spatial data can be used to make such

predictions. Often a variable such as the depth of a water table or the

thickness of a coal deposit shows regional dependence, which means that

its value at two or more locations close to each other is relatively similar.

For example, the percentage yield of a deposit of gold-bearing rock might be

1.1 g/ton and 1.2 g/ton at two sites only 100 meters apart, but 1.1 and

5.6 g/ton at sites 1200 meters apart. This is just the same as positive

Table 22.4 Summary data, for the direction, in degrees, of the 250 streams

in Table 22.3 with the expected number within each bin if the objects

sampled are equally likely to face in any direction.

Direction Observed frequencies Expected

1–60 63 41.66

61–120 31 41.66

121–180 20 41.66

181–240 22 41.66

241–300 41 41.66

301–360 73 41.66

352 Introductory concepts of spatial analysis