Steve M., Darby D.M., Geostatistics Explained - An Introductory Guide for Earth Scientists

Подождите немного. Документ загружается.

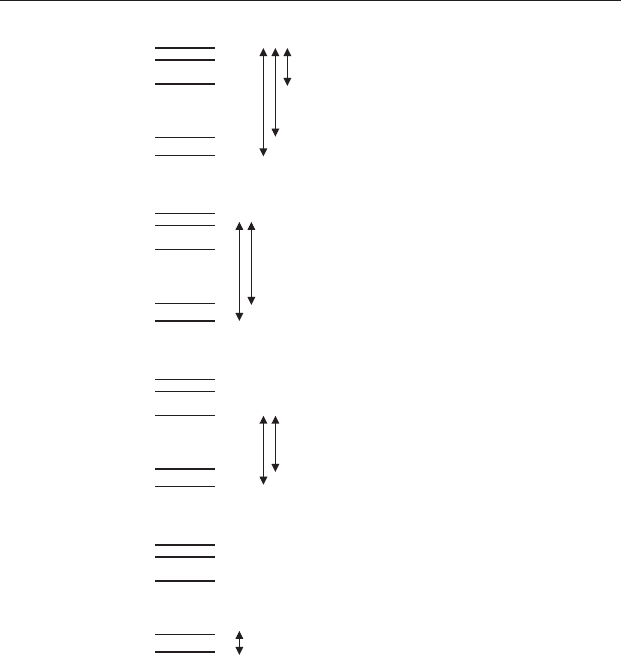
(a)

(b)

(c)

(d)

(A–E and A–D are significant)

(A–C is not significant)

(B–E and B–D are significant)

(C–E and C–D are significant)

(D–E is not significant)

Figure 11.1 General procedure for a Tukey a posteriori test. The treatment

means (A to E) are displayed in order of magnitude from the smallest (E) to

the largest (A). (a) First the largest mean is compared to the smallest (A–E).

If the diﬀerence is signiﬁcant, the largest is then compared to the second

smallest (A–D) and so on, until a non-signiﬁcant diﬀerence (here, as an

example, A–C) is found or there are no more pairs of means left to compare.

All means included within the range between A–C (A, B and C) are assigned to

the same population. (b) Testing continues using the same procedure but

starting with the second largest mean and comparing it to the smallest (B–E).

(D) is compared to E. This diﬀerence is not signiﬁcant so D and E appear to be

from the same population, which has a diﬀerent mean to the one from which

A, B and C have been taken.

11.2 Multiple comparison tests after a Model I ANOVA 133

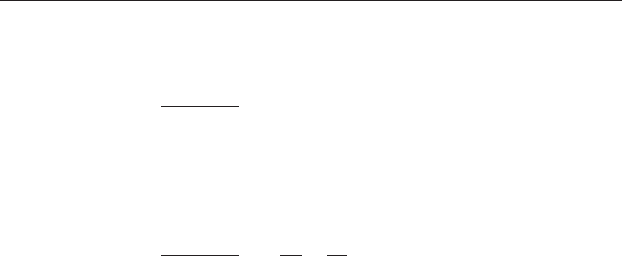
then the standard error of the mean estimated from an ANOVA is:

SEM ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

MS error

(11:3)

where n is the sample size of each treatment. If the treatment sample sizes

are diﬀerent, you use the formula:

SEM ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

MS error





(11:4)

where n

and n

are the numbers in each of the two treatments being

compared.

Then you calculate the Tukey statistic q for each pair of means by using

Equation (11.1) and the procedure in Figure 11.1. The value of q will be zero

when there is no diﬀerence among the two sample means and will increase

as the diﬀerence between the means increases. If q exceeds the critical value,

the hypothesis that the means are from the same population is rejected.

The critical value of q depends on your chosen value of α, the number of

degrees of freedom for the MS error and the number of means being tested.

Here we deliberately have not given a table of q values because most

statistical packages will do multiple comparisons and even generate a dis-

play assigning the sample means to groups that appear to be from the same

population. Section 11.3 gives three examples and also illustrates that

ambiguous results are possible.

11.3 An a posteriori Tukey comparison following a signiﬁcant

result for a single-factor Model I ANOVA

11.3.1 Trace elements in New England granites

Trace elements (especially the rare earth elements, Zr, Hf, Ta, Sc and Th) are

very useful for understanding crystallization histories and origins of granitic

magmas. The relative abundances of these elements are often used as

“ﬁngerprints” to determine if geographically separated granite outcrops

have come from the same parent magma. Table 11.1 gives data for the

hafnium (Hf) contents of four diﬀerent granitic bodies in New England.

This is a Model I ANOVA, because the researcher is only interested in the

granite at these four locations.

134 Multiple comparisons after ANOVA

If you run a single-factor ANOVA on the data in Table 11.1 you will

obtain an F ratio (F

3,16

) of 74.01, which has a probability of less than 0.001.

Therefore, at least some of the treatment means appear to be from diﬀerent

populations. If you then run an a posteriori Tukey test you will ﬁnd that all

four means appears to be from four distinctly diﬀerent populations.

11.3.2 Stable isotope data from tourmalines in Maine

Table 11.2 gives data for the δ

O values for tourmalines from three local-

ities in western Maine: the Sebago Batholith, Black Mountain and Mount

Mica. Here too the mean δ

O values can be used to help decide whether

the tourmalines have originated from the same or diﬀerent parent magmas.

A single-factor ANOVA will give an F ratio (F

2,9

) of 12.06, which has a

probability of 0.003. At least two treatment means do not appear to be from

the same population.

Table 11.1 Hf contents in (μg/g) of four diﬀerent New England granites.

Cape Dan Seabody Wincy Easterly

16 19 25 12

14 20 30 10

16 22 26 12

17 20 27 13

18 24 28 9



X 16.2 21.0 27.2 11.2

Table 11.2 δ

O values for tourmalines from three localities in western

Maine: the Sebago Batholith, Black Mountain and Mount Mica.

Sebago Batholith Black Mountain Mount Mica

12.2 12.4 14.8

13.1 12.6 13.2

12.7 12.1 13.5

12.6 11.9 14.6



X 12.65 12.25 14.03

11.3 The Tukey test 135

If you run an a posteriori Tukey test it will show that means for the Sebago

Batholith and Black Mountain appear to be from the same population, while

the mean for Mount Mica appears to be from another with a signiﬁcantly

greater δ

Ovalue(Figure 11.2).

11.3.3 Apatite in sandstone

The percentage of apatite in sandstone shows considerable variation and

can be used to determine the source areas for these sediments. Table 11.3

gives data for the modal abundance of apatite at three diﬀerent locations.

A single-factor ANOVA analysis gives an F ratio (F

2,9

) of 10.8, which has a

probability of 0.004. The three treatment means do not appear to be from

the same population.

If, however, you run an a posteriori Tukey test it will show that means for

Darcy and Runcan appear to be from the same population, while the means

for Runcan and Alinda appear to be from another.

This result (Figure 11.3) is obviously ambiguous. The a posteriori analysis

has separated the data into two subsets, but the mean of the Runcan sand-

stone cannot be distinguished from the means of either the Darcy or the

Alinda sandstone. At the same time, the mean of the Darcy can be distin-

guished from the mean for Alinda. Therefore, it seems at least one Type 2

error has been committed somewhere because the mean of the Runcan

sandstone has been assigned to two diﬀerent populations. This is a common

problem and is discussed in more detail in the following two sections.

11.3.4 Power and a posteriori testing

Chapter 10 began with a discussion about the danger of an increased

probability of Type 1 error when making numerous pairwise comparisons

14.03

12.65

12.25

Mount Mica

Sebago

Black Mountain

Figure 11.2 Summary of the results of an a posteriori Tukey test comparing

among the means of the three samples in Table 11.2 . Treatment means

connected by vertical lines are not signiﬁcantly diﬀerent.

136 Multiple comparisons after ANOVA

among three or more means. Here, however, the a posteriori method for

identifying which treatment means appear to be from the same population

uses numerous pairwise comparisons. Therefore, you may be thinking that

this procedure will also have an increased risk of Type 1 error.

First, however, unplanned a posteriori comparisons are usually only

made across all groups if the ANOVA has detected a signiﬁcant diﬀerence

among the treatment means. Second, a posteriori tests are speciﬁcally

designed to take into account the number of means being compared and

have a much lower risk of Type 1 error than the same number of t tests.

Unfortunately this makes multiple comparison tests relatively low in power,

which is why they can give ambiguous results such as the one in

Section 11.3.3. In more extreme cases it sometimes happens that an

ANOVA detects a signiﬁcant diﬀerence, but subsequent a posteriori testing

fails to detect a signiﬁcant diﬀerence among any means. One solution is

to increase the sample size of each group or treatment (Chapter 8).

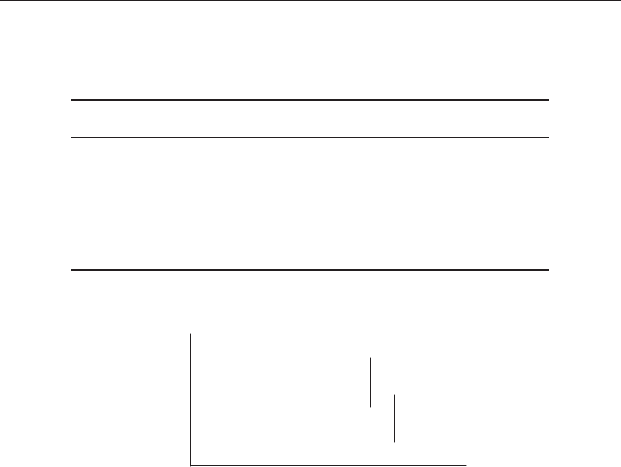
Darcy

Runcan

Alinda

% Apatite

9.0

6.0

3.0

Figure 11.3 Summary of the results of an a posteriori Tukey test comparing

among the means of the three samples in Table 11.3 . Treatment means

connected by vertical lines are not signiﬁcantly diﬀerent. The test has assigned

the mean for Runcan into two groups (Darcy/Runcan) and (Runcan/Alinda)

so at least one Type 2 error has occurred.

Table 11.3 The modal percentage of apatite in sandstones from

three diﬀerent basins.

Darcy Runcan Alinda

74 1

85 2

10 7 4

11 8 5



X 9.0 6.0 3.0

11.3 The Tukey test 137

11.4 Other a posteriori multiple comparison tests

There are many other multiple comparison tests. These include the LSD,

Bonferroni, Scheﬀe and Student–Newman–Keuls. The most commonly

used are the Tukey and Student–Newman–Keuls (Zar, 1996). Most statis-

tical packages oﬀer you a wide choice of these tests, the relative merits of

which are discussed in more advanced texts.

11.5 Planned comparisons

Instead of making a large number of indiscriminate unplanned a poste-

riori comparisons, a better a pproach can be to make a small number of

more careful (a priori m eaning “before the event”) comparisons. For

example, in Section 11.3.2 you may have a good reason based on outcrop

appearance or geographical proximity to propose the following two a

priori hypotheses: “ Oxyg en isotopic r atios of tourmalines at Black

Mountain are signiﬁcantly diﬀerent than those at Mount Mica” and

“Oxygen isotopic ratios of tourmalines at Black Mountain are signiﬁ-

cantly diﬀerent than those at the Sebago Batholith.” An ANOVA will test

for diﬀerences among treatments with an α of 0.05 and also give a good

estimateofthesamplevariancefrom the MS error, since this has been

calculated from all the individuals used for this overall comparison. Next,

however, instead of making a large number of unplanned comparisons,

you could carry out two t tests comparing the mean oxygen isotopic ratio

at B lack Mountain and Mount Mica, and Black Mounta in and the Sebago

Batholith.

If you make only one planned comparison the probability of Type 1 error

is an acceptable 0.05. If you make several a priori comparisons that really

have been planned for particular reasons before the experiment (e.g. the

two listed above), then each is a distinct and diﬀerent hypothesis, so the risk

of a Type 1 error is still an acceptable 0.05. It is only when you make

indiscriminate comparisons that the risk of Type 1 error increases and

you should consider using one of the a posteriori tests described previously,

which maintains an α of 0.05.

To make a planned comparison after a single factor ANOVA you use the

formula for a t test from Chapter 8 except that you use the mean square

error as the best estimate of s

138 Multiple comparisons after ANOVA

nAþnB2







ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

MS error





(11:5)

which reduces to Equation (11.6) when there are equal numbers in both

treatment groups:

nAþnB2







ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2MS error

(11:6)

Here is an example, using the data from Example 2 in Section 11.3.2.

From the ANOVA, the mean square for error is 0.288. The mean of the

Black Mountain tourmaline δ

O is 12.25 ‰ and Mount Mica is 14.03 ‰.

Therefore:

12:25  14:03

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

20:288

¼4:69

From Table 8.1 the critical two-tailed 5% value for t is ± 2.447. The two

means appear to be from diﬀerent populations. This supports the idea that

these two pegmatites crystallized from unrelated magmas.

The planned comparison to test the Sebago Batholith tourmaline com-

pared to Black Mountain is:

12:65  12:25

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

20:288

¼ 1:05

The critical two-tailed 5% value for t is ± 2.447, so these two means do not

appear to be from diﬀerent populations.

Although you are likely to examine other diﬀerent types of chemical data

to further test this conclusion, it appears plausible that the Black Mountain

and Mount Mica pegmatites do not share parent magmas, but the Sebago

Batholith and the Black Mountain pegmatite do originate from the same

parent. Note that this result is consistent with the Tukey test of these data in

Section 11.3.2.

Finally, here are two planned comparisons applied to the data for apatite

content of sandstones in Table 11.3. Your a priori hypotheses are: “The

percentage of apatite in Runcan sandstone is diﬀerent from that in Darcy”

11.5 Planned comparisons 139

and “The percentage of apatite in Runcan sandstone is diﬀerent from that

in Alinda.” Again, the MS error from an initial ANOVA will give a good

estimate of the variance.

For the comparison between Runcan and Darcy:

6:00  9:00

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

23:33

¼2:5

Since the critical two-tailed 5% value for t is ± 2.447, these two means appear

to be from diﬀerent populations. Note that this result is diﬀerent from the

one from the (ambiguous) Tukey test of the same data in Section 11.3.3,

which did not separate Runcan and Darcy.

For the comparison between Runcan and Alinda:

6:00  3:00

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

23:33

¼2:5

Here too, since the critical two-tailed 5% value for t is ± 2.447, these two means

also appear to be from diﬀerent populations. Again, note that this result is

diﬀerent from the one from the Tukey test of the same data in Section 11.3.3,

which did not separate Runcan and Alinda. The a priori test has more power.

This example particularly illustrates the value of planned comparisons.

Both the Darcy and Alinda sandstones appear to be distinct from the

Runcan, at least on the basis of their apatite content. This conclusion is

diﬀerent from the one made on the basis of the less powerful Tukey test

(Section 11.3.3) which could not separate the intermediate percentage for

Runcan from the higher percentage of Darcy or the lower one of Alinda

(and thus included a Type 2 error).

Importantly, you should only make a planned comparison if you really do

have a plausible hypothesis to justify this procedure. It is not appropriate or

ethical to examine the results of a Tukey test and say, in hindsight, “These

two means are almost signiﬁcantly diﬀerent, so I will run a t test on them

because it is likely to be more powerful.”

11.6 Questions

(1) A petroleum scientist was given the following data for the ﬂow rate (in

barrels per day on eight days) for three speciﬁcally chosen oil wells in

140 Multiple comparisons after ANOVA

the Timor Sea, and was asked to identify the one which was producing

signiﬁcantly more oil. (a) Does a single-factor ANOVA give a signiﬁ-

cant result? (b) Is a posteriori testing needed? If so, which well is

yielding the most oil and is it signiﬁcantly diﬀerent to the other two?

RVB1 RVB2 RVB3

157 183 149

184 174 193

143 182 129

135 199 146

163 183 126

103 168 132

152 193 143

129 162 154

(2) In relation to the data in Question 1, wells RVB1 and RVB3 are only

1 km apart and the oil company was particularly interested in whether

the two wells were yielding diﬀerent amounts. Use a t test to make a

planned comparison between wells RVB1 and RVB3 only. Is the result

signiﬁcant?

11.6 Questions 141

12 Two-factor analysis of variance

12.1 Introduction

A single-factor ANOVA gives the probability that two or more sample

means have come from populations with the same mean (Chapter 10),

but can only be used to analyze univariate data from samples exposed to

diﬀerent levels or aspects of only one factor. For example, it could be used to

compare the diﬀusivity of hydrogen through olivine (the variable) at two or

more temperatures (the factor), the percentage of feldspar crystals (the

variable) in successive layers of an intrusive complex (the factor), or the

salinity of seawater (the variable) from several diﬀerent depths (the factor).

Often, however, scientists obtain univariate data in relation to more than one

factor.Examplesoftwo-factorexperimentsare the phase equilibrium of alumi-

nosilicates (Al

SiO

) at several combinations of temperature and pressure, the

growth of crystals as a function of magmatic H

O and cooling rate, or the

likelihood of snow as a function of varying humidity levels and temperatures.

It would be very useful to have an analysis that gave separate F ratios (and the

probability that the treatment means had come from populations with the same

mean) for each of the two factors. That is what two-factor ANOVA does.

12.1.1 Why do an experiment with more than one factor?

Experiments that simultaneously include the eﬀects of more than one factor

on a particular variable may be far more revealing than looking at each

factor separately because you may detect certain combinations of factors

that have a synergistic eﬀect. Also, by examining several factors at once,

there may be signiﬁcant savings in time and resources compared to doing a

series of separate experiments and separate analyses.

Here is an example of the advantage of a two-factor experiment. It also

illustrates a synergistic eﬀect – what statisticians call interaction – which

occurs when the eﬀect of one factor varies across the levels of the other.

142