Стародубцев В.С. Экологическая геодинамика
Подождите немного. Документ загружается.

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ»
В.С. Стародубцев
ЭКОЛОГИЧЕСКАЯ
ГЕОДИНАМИКА
Учебное пособие для вузов
Издательско-полиграфический центр
Воронежского государственного университета
2008
2
УДК 51
С 77
Печатается по решению учебно-методического совета геологиче-
ского факультета Воронежского государственного университета от
25 октября 2007 г.
Стародубцев В.С.
С77 Экологическая геодинамика : учеб. пособие для вузов / В.С. Старо-
дубцев. – Воронеж : Издательско-полиграфический центр Воронеж-
ского государственного университета, 2008. – 44 с.
В пособии подробно рассматриваются особенности изучения миграции под-
земных вод, а также проблемы устойчивости оползневого склона. Материал из-
лагается с большим количеством примеров по принципу: «Читай, смотри и де-
лай» с наличием самостоятельных задач для контроля пройденных разделов.
Учебное пособие по курсу «Экологическая геодинамика» предназначено для
студентов очной формы обучения по специальности «Экологическая геология».
УДК 51
© Стародубцев В.С., 2008
© Издательско-полиграфический
центр Воронежского государст-
венного университета, 2008
3
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ........................................................................................................ 4
ЛАБОРАТОРНАЯ РАБОТА № 1 Интерполяция функций
эколого-геологических процессов................................................................... 5
ПОСТАНОВКА ЗАДАЧИ ................................................................................ 6
ВАРИАНТЫ ЗАДАНИЙ
................................................................................................10
ЛАБОРАТОРНАЯ РАБОТА № 2 Прогноз конвективного
массопереноса загрязняющих компонентов подземных вод........................ 12
ПОСТАНОВКА ЗАДАЧИ ................................................................................ 16
ЛАБОРАТОРНАЯ РАБОТА № 3 Расчет устойчивости
оползневого склона ........................................................................................... 18
3.1. Формы нарушения устойчивости склонов....................................... 24
3.2. Устойчивость свободных откосов и склонов.................................... 25
3.3. Устойчивость свободных откосов и склонов,
сложенных связанными грунтами ..........................................................................26
ПОСТАНОВКА ЗАДАЧИ ................................................................................ 29
ВАРИАНТЫ ЗАДАНИЙ .................................................................................. 30
4
ВВЕДЕНИЕ
Настоящее учебное пособие к лабораторным работам по курсу «Эко-
логическая геодинамика» предназначено для студентов V курса обучаю-
щихся на геологическом факультете по специальности 020306 – Экологи-
ческая геология.
Курс посвящен изучению геологических и инженерно-геологических
процессов и явлений в связи с инженерно-хозяйственной деятельностью
человека и решением различных эколого-геологических проблем. Главные
задачи
курса заключаются в развитии у студентов профессиональных ин-
женерно-геологических навыков и знаний о геологических и инженерно-
геологических процессах и явлениях, их анализе, методах прогнозирова-
ния, способах инженерной защиты, необходимых им для изучения и оцен-
ки экологических функций литосферы.
Лабораторные работы проводятся в девятом семестре по трем темам:
1. Интерполяция функций
эколого-геологических процессов 4 часа
2. Прогноз конвективного массопереноса загрязняющих
компонентов подземных вод 4 часа
3. Расчет устойчивости оползневого склона 6 часов

5
ЛАБОРАТОРНАЯ РАБОТА № 1
Интерполяция функций эколого-геологических процессов
Лабораторная работа предназначена для уяснения лекционных тем:
«Заиление водохранилищ», «Природные и техногенные факторы заиле-
ния», «Заболачивание», «Условия их возникновения, влияние состава грун-
тов и режима грунтовых вод», «Особенности изысканий в районах распро-
странения болот», «Подтопление», «Природные и техногенные факторы
подтопления», «Изучение и
оценка опасности подтопления».
Особенности интерполяции функций эколого-геологических процес-
сов рассмотрим на примере функции напора подземных вод, как наиболее
интересной с точки зрения влияния на формирование и развитие большин-
ства эколого-геодинамических процессов и явлений.
Рассмотрение области фильтрации подземных вод как объекта иссле-
дований при изучении эколого-гидродинамических закономерностей гео-
фильтрации всегда бывает затруднено малым количеством фактических
данных. Это, прежде всего, относится к гидродинамическим параметрам
пласта. Важнейшим среди них является напор подземных вод, который
входит как искомая функция во все дифференциальные уравнения гео-
фильтрации. Преодоление этих затруднений связано с применением мето-
дов интерполяции функций.
Интерполяция (от латинского interpolatio – обновление, переделыва-
ние, изменение
) – приближенное или точное нахождение какой-либо вели-
чины по известным отдельным значениям этой же или других величин,
связанных с ней. В первоначальном понимании – восстановление функций
(точное или приближенной) по известным её значениям в заданных точках.
В гидрогеологии применяется для построения различных карт и подготов-
ки начальных условий при решении дифференциальных
уравнений гео-
фильтрации численными методами. Наиболее популярны кусочно-
линейная интерполяция, кусочно-квадратичная интерполяция, интерполя-
ция квадратичными сплайнами. В лабораторной работе используется ку-
сочно-линейная интерполяция.
Пусть надо вычислить f(x) для х
∈
[х
i
, х
i+1
], h = х
i+1
– х
i
. Тогда суть
кусочно-линейной интерполяции состоит в том, что используется линей-
ное приближение
f(x)
≈
f
i
+
ff
h
ii+
−
1
(x - x
i
). (1)
Для случая равномерной сетки на отрезке [i,j] выражение (1) преобра-
зуется к виду
f
i+1
≈
f
i
+
ji
ff
ji
−
−
, (2)
где i и j – номер узла сетки.
6
Таким образом, непрерывная функция напора заменяется в области
фильтрации дискретной (сеточной) функцией, значения которой известны
лишь в некоторых узлах сетки и с помощью методов интерполяции нахо-
дятся ее значения во всех узлах сетки.
ПОСТАНОВКА ЗАДАЧИ
Дано
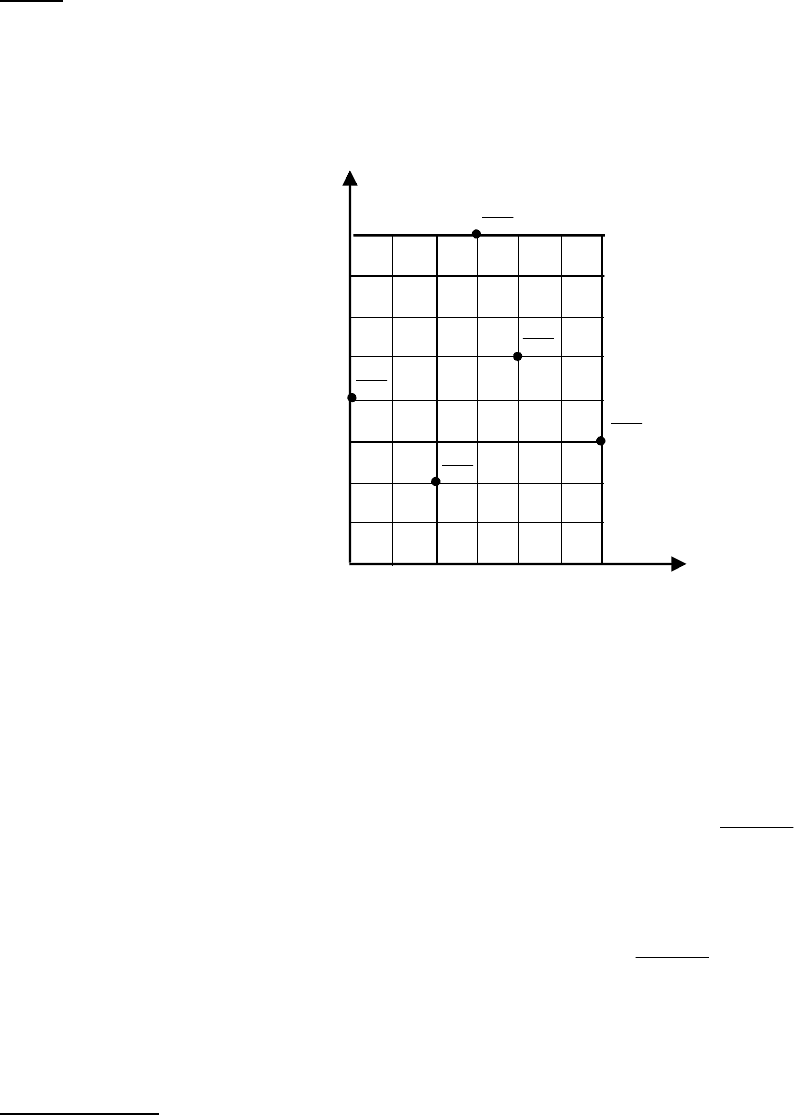
Область фильтрации, которая представлена участком речной долины
протяженностью 1200 м на 1600 м, разбита сеткой с равномерным шагом
по X и по Y и равным 200 м, где значения функции напора известны лишь
в отдельных узлах сетки (рис. 1).
Требуется
¾ найти значения функции во всех узлах сетки, построить линии рав-
ных напоров с шагом 0,5 метра
и линии тока;
¾ используя линии гидроизогипс и закон Дарси Q = K
ф
F
12
L
HH
−
= K
ф
FI,
где F – площадь поперечного водоносного пласта, м
2
; Н
1
и Н
2
– значения
напора в рассматриваемых сечениях, м; L – длина пути фильтрации,
м, К
ф
– коэффициент фильтрации, м/сут., I =
12
L
HH
−
– значение на-
порного градиента; Q – расход потока, м
3
/сут.,
¾ рассчитать водоприток в речную долину, учитывая, что К
ф
= 40 м/сут.,
а h = 50 м.
Выполнение
Для удобства примем следующую индексацию узлов:
Река
(абсолютная отметка уровня воды в реке 100 м)
Водораздельное
пространство
100.0
100.0 100.0 100.0 100.0 100.0
100.0
X
Y
1 2 3 4 5 6 7
1
2
3
4
5
6
7
8
9
скв.1
99.0
скв.5
108.0
скв.2
103.0
скв.4
105.0
скв.3
104.0
Рис.1. Задание к лабораторной работе №1
Рис. 1. Задание к лабораторной работе № 1
7
по Х – i = 1,…7;
по Y – j = 1,…9.
Тогда получим обозначение значения напора в узле H
i,j
. Например, значе-
ние напора в скважине № 4 можно записать как H
5,6
= 105,0 м.
Принимаем, что на водораздельном пространстве напор во всех узлах
одинаков (H
1,9
= H
2,9
= … = H
4,9
=…= H
7,9
). Находим значения напора в ос-
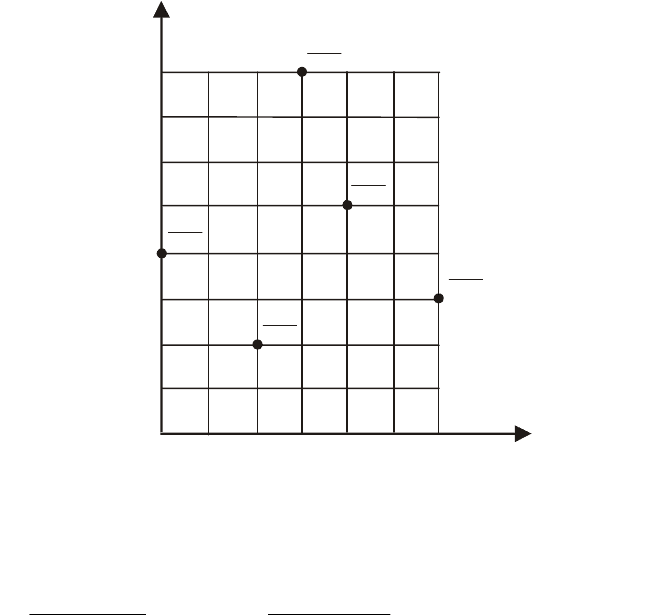
тавшихся граничных узлах (левая и правая границы). Для этого интерпо-
лируем значение напора между узлами H
1,1
и H
1,5
, H
1,5
и H
1,9
, а также между
H
7,1
и H
7,4
, H
7,4
и H
7,9
согласно выражению (2). Например:
H
1,2
= H
1,1
+
1,5 1,1
1,1
104,0 100,0
51 4
HH
H
−
−
=+
−
= H
1,1
+1 = 100 + 1 = 101,0 м,
Используя известные внутренние точки H
3,3
и H
3,7
находим значения
напора в узлах Н
1,3
– H
3,3
и Н
3,3
– H
7,3
и аналогично Н
1,6
– H
5,6
и Н
5,6
– H
7,6
(рис. 2).
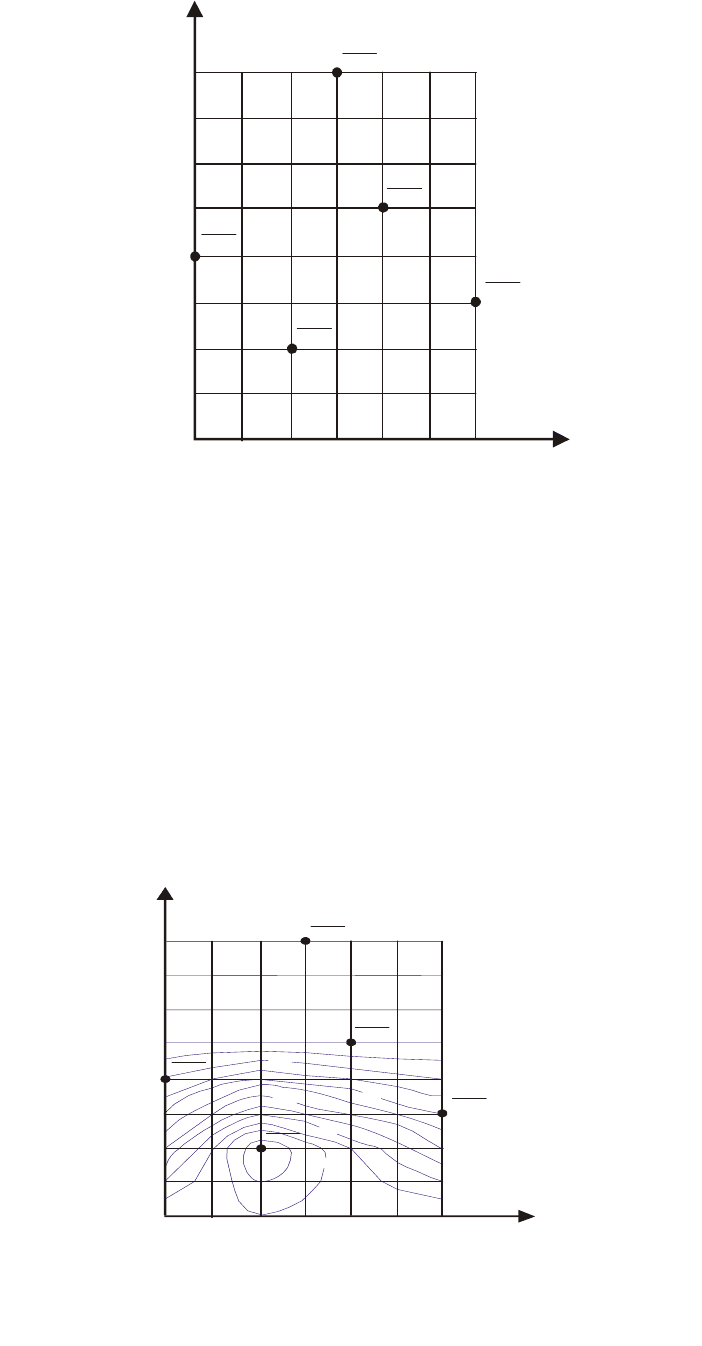
Интерполяция заканчивается нахождением значений напора в проме-
жуточных строках (H
i,2
, H
i,4
, H
i,5
, H
i,7
, H
i,8
). Для этого последовательно
интерполируем между строками H
i,3
– H
i,1
, H
i,6
– H
i,3
, H
i,9
– H
i,6
(рис. 3).
В гидрогеологии линии напряженности называют линиями тока, а эк-
випотенциальные поверхности Н – поверхностями равных напоров (для
напорных потоков – гидроизопьезы, для безнапорных – гидроизогипсы).
Река
(абсолютная отметка уровня воды в реке 100 м)
Водораздельное
пространство
100.0
100.0 100.0 100.0 100.0 100.0
100.0
X
Y
1 2 3 4 5 6 7
1
2
3
4
5
6
7
8
9
скв.1
99.0
скв.5
108.0
скв.2
103.0
скв.4
105.0
скв.3
104.0
Рис.2. Интерполяция области фильтрации
102.0
105.0
105.0
105.0
105.0
105.0
105.0
104.0
102.0
101.0
100.5 99.75
100.5
101.25
106.0
106.0
107.0
107.0
108.0
108.0
108.0
108.0 108.0
108.0
103.0
101.0
Рис. 2. Интерполяция области фильтрации
8
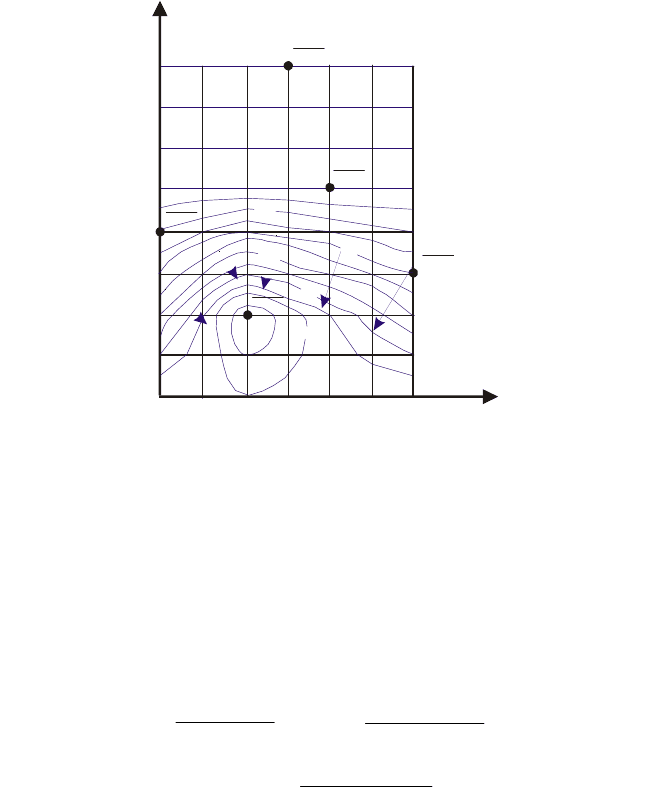
Построение линий равных напоров (гидроизогипс) аналогично процессу
интерполяции узлов сетки области фильтрации. Отличие состоит лишь в том
что интерполяция идет теперь по отдельным узлам. Так, между узлами Н
2,3
–
H
3,3
следует найти точки прохождения гидроизогипс 99,5 м и 100,0 м. Заме-
тим, что интерполяция должна проводится как по горизонтальной, так и по
вертикальной осям. Гидроизогипсы 105,0–108,0 совпадут с линиями сетки,
так как радиус влияния ЭС № 1 составляет ≈ 400 м (рис. 4).
Река
(абсолютная отметка уровня воды в реке 100 м)
Водораздельное
пространство
100.0
100.0 100.0 100.0 100.0 100.0
100.0
X
Y
1 2 3 4 5 6 7
1
2
3
4
5
6
7
8
9
скв.1
99.0
скв.5
108.0
скв.2
103.0
скв.4
105.0
скв.3
104.0
101.0
102.0
103.0
105.0
105.0
105.0
105.0
105.0
105.0
104.0
102.0
101.0
103.5
102.0
100.5
103.0
101.0
100.25 99.5
103.25
101.5
99.75
99.88
103.5
102.0
100.5
100.25
103.75
102.5
101.25
100.63
106.0
106.0
106.0
106.0 106.0 106.0
106.0
107.0
107.0
107.0
107.0 107.0 107.0
107.0
108.0
108.0
108.0
108.0 108.0
108.0
Рис.3. Интерполяция области фильтрации
Река
(абсолютная отметка уровня воды в реке 100 м)
Водораздельное
пространство
100.0
100.0 100.0 100.0 100.0 100.0
100.0
X
Y
1 2 3 4 5 6 7
1
2
3
4
5
6
7
8
9
скв.1
99.0
скв.5
108.0
скв.2
103.0
скв.4
105.0
скв.3
104.0
Рис.4. Линии равных напоров (гидроизогипсы)
101.0
102.0
103.0
105.0
105.0
105.0
105.0
105.0
105.0
104.0
102.0
101.0
103.5
102.0
100.5
103.0
101.0
100.25 99.5
103.25
101.5
99.75
99.88
103.5
102.0
100.5
100.25
103.75
102.5
101.25
100.63
106.0
106.0
106.0
106.0 106.0 106.0
106.0
107.0
107.0
107.0
107.0 107.0 107.0
107.0
108.0
108.0
108.0
108.0 108.0
108.0
100.0
101.0
102.0
103.0
104.0
Рис. 3. Интерполяция области фильтрации
Рис. 4. Линии равных напоров (гидроизогипсы)
9
Линии тока целесообразно строить в местах изгиба линий равных
напоров (рис. 5).
Для определения водопритока выбираем параллельные линии гидро-
изогипс (чтобы снизить погрешность при определении площади попереч-
ного сечения потока подземных вод) и с учетом шага сетки вычисляем во-
доприток в речную долину со стороны водораздела. Например:
Q = K
ф
F
12
HH
L
−
= K
ф
F
L
HH
6,47,4
−
=
= 40 м/сут
(50 м × 200 м × 6)
0.200
0.1050.106
−
= 12000 м
3
/сут.
Литература
1. Мироненко В.А. Динамика подземных вод [Текст] / В.А. Мироненко. –
М. : Изд-во МГУ, 1996. – 519 с.
2. Миpоненко В.А. Теоpия и методы интеpпpетации опытно-фильтpационных
pабот [Текст] / В.А. Миpоненко, В.М. Шестаков. – М. : Hедpа, 1978. – 325 с.
3. Шестаков В.М. Динамика
подземных вод [Текст] / В.М. Шестаков –
М. : Изд-во МГУ, 1979. – 418 с.
Река
(абсолютная отметка уровня воды в реке 100 м)
Водораздельное
пространство
100.0
100.0 100.0 100.0 100.0 100.0
100.0
X
Y
1 2 3 4 5 6 7
1
2
3
4
5
6
7
8
9
скв.1
99.0
скв.5
108.0
скв.2
103.0
скв.4
105.0
скв.3
104.0
Рис.5. Линии равных напоров (гидроизогипсы)
и линии тока потока подземных вод
101.0
102.0
103.0
105.0
105.0
105.0
105.0
105.0 105.0
104.0
102.0
101.0
103.5
102.0
100.5
103.0
101.0
100.25 99.5
103.25
101.5
99.75
99.88
103.5
102.0
100.5
100.25
103.75
102.5
101.25
100.63
106.0
106.0
106.0
106.0 106.0 106.0
106.0
107.0
107.0
107.0
107.0 107.0 107.0
107.0
108.0
108.0
108.0
108.0 108.0
108.0
100.0
101.0
102.0
103.0
104.0
Рис. 5. Линии равных напоров (гидроизогипсы)
и линии тока потокаподземных вод

10
ВАРИАНТЫ ЗАДАНИЙ
№
вар.
№
скв.
X Y H h K
a
№
вар.
№
скв.
X Y H h K
a
1 1 1 3 101.0 32.5 38 21 1 1 6 105.3 18.4 26.4
2 1 7 105.0 2 4 3 99.4
3 3 3 99.66 3 7 5 103.6
4 5 5 102.42 4 2 7 106.4
5 7 6 104.0 22 1 1 5 104.6 26.7 34.7
2 1 1 4 102.0 20.0 33.0 2 3 3 99.3
2 3 5 101.82 3 4 7 105.7
3 4 3 99.66 4 7 6 104.7
4 7 3 101.0 23 1 1 5 104.5 37.2 32.1
5 7 6 104.0 2 4 4 98.7
3 1 1 6 104.8 26.0 30.4 3 4 7 104.3
2 4 3 99.5 4 7 5 104.0
3 4 5 101.7 24 1 1 6 105.0 33.9 26.9
4 7 3 102.4 2 4 3 99.7
5 4 8 106.1 3 7 5 105.0
4 1 1 5 103.2 43.0 27.4 4 4 7 104.1
2 4 3 99.5 25 1 1 5 104.7 28.4 30.7
3 4 4 100.3 2 3 3 99.3
4 4 5 101.7 3 7 5 104.6
5 7 6 104.4 4 5 7 105.3
5 1 1 6 104.0 17.0 22.2 26 1 1 6 105.3 30.8 22.4
2 3 3 99.66 2 4 3 99.7
3 5 5 100.82 3 7 5 105.2
4 7 4 102.0 4 4 6 105.0
6 1 1 6 104.0 29.0 23.2 27 1 1 5 104.7 22.9 34.7
2 4 3 101.0 2 3 3 99.5
3 5 6 102.66 3 7 4 104.7
4 7 7 104.5 4 3 7 105.7
7 1 1 4 102.5 27.4 30.4 28 1 1 5 104.6 26.3 29.4
2 2 3 99.6 2 3 3 99.2
3 2 7 103.5 3 7 4 105.8
4 7 5 103.1 4 4 4 102.3
8 1 1 4 102.5 19.3 26.8 29 1 1 6 106.2 23.7 29.8
2 4 3 101.0 2 4 3 99.6
3 3 6 101.4 3 4 5 103.8
4 7 5 102.9 4 7 5 106.7
9 1 1 4 103.1 24.3 40.3 30 1 1 5 105.3 35.6 36.4
2 4 3 99.0 2 5 3 99.1
3 4 5 101.3 3 7 5 106.2
4 4 7 102.1 4 4 5 103.4
5 7 6 103.5 31 1 1 4 104.5 32.8 25.4
10 1 1 4 102.7 31.1 29.7 2 3 3 98.3
2 2 7 103.0 3 5 5 104.3
