Стариков А.В., Кущева И.С. Экономико-математическое и компьютерное моделирование: методические указания

Подождите немного. Документ загружается.

абсцисс, полагая в (1.8) х

=0:

)(0

x =14,4/0,06=240. Этим же способом строятся

прямые, соответствующие ограничениям (1.9) и (1.10).

В результате получается шестиугольник, вершины которого обозначены

цифрами от 0 до 5. Этот шестиугольник, включая ограничивающие его линии, и

есть область допустимых решений рассматриваемой задачи – симплекс. Любая

точка с соответствующими ей координатами х

и х

, лежащая внутри или на

границе симплекса, удовлетворяет системе ограничений (1.7) – (1.11). Теперь

необходимо из всех точек найти ту, в которой критерий эффективности (1.6)

имеет наибольшее из всех возможных значений. Строится прямая,

соответствующая (1.6). Для этого правой части (1.6) дается некоторое

конкретное значение, например, в рассматриваемом случае – 400. Тогда целевая

функция пройдет через точки х

= 108,108 и х

= 100 (положение I на рис. 1.1).

Эта прямая проходит под углом α к оси абсцисс, который определяется

соотношением прибылей от обоих видов продукции

tgα = 3,7/4 = 0,925. Если изменять величины прибылей (одной или обеих), угол

наклона α также будет меняться. Если полученную прямую I перемещать

параллельно самой себе в сторону увеличения х

и х

(это соответствует

увеличению правой части), то она в итоге займет положение II, в котором имеет

с симплексом единственную общую точку (точку 3). Именно эта точка с

координатами х

=90 и х

=90 доставляет максимальное значение критерию

эффективности. Суммарная прибыль в этой точке достигает максимального

значения 90⋅3,7+90⋅4=693 р.

В табл. 1.2 приведены координаты всех точек – вершин симплекса,

полученные из рис. 1.1, а также значения критерия эффективности в этих

точках, вычисленные по формуле (1.6).

Таблица 1.2

№ вершины симплекса 0 1 2 3 4 5

Шкафы (х

)

0 0 40 90 130 130

Кровати (х

)

0 120 120 90 40 0

Полная прибыль (Z) 0 480 628 693 641 481

Анализ данных табл. 1.2 показал, что наибольшее значение критерия

эффективности достигается в точке 3. Так как эта точка лежит на пересечении

прямых, соответствующих ограничениям (1.8) и (1.9), то можно сделать вывод,

что оптимальное решение ограничено ресурсами пиломатериалов и

оборудования, которые при плане, соответствующем точке 3, будут полностью

израсходованы, тогда как ресурсы обивочной ткани и древплиты (например,

ДСтП или ДВП) будут израсходованы лишь частично. В табл. 1.3 представлены

результаты расчета затрат всех видов ресурсов, а также остатков ресурсов для

всех планов выпуска продукции, соответствующих всем вершинам симплекса.

Задание 2. Выполнить графический анализ модели, для чего построить

область допустимых планов (симплекс), найти все допустимые планы выпуска

мебели, соответствующие вершинам симплекса. Графическим методом найти

оптимальный план, установить, какие виды ресурсов его определяют.

Выполнить количественную оценку прибыли для всех допустимых планов,

соответствующих вершинам симплекса, убедиться, что оптимальный план,

найденный при графическом анализе, обеспечивает наибольшую прибыль.

Таблица 1.3

Вершины симплекса 0 1 2 3 4 5

Ткань 0 396 396 297 132 0

Расход Пиломатериалы 0 12 14,4 14,4 11,8 7,8

ресурсов Оборудование 0 480 680 810 810 650

Древплита 0 0 100 225 325 325

Ткань 396 0 0 99 264 396

Остаток Пиломатериалы 14,4 2,4 0 0 2,6 6,6

ресурсов Оборудование 810 330 130 0 0 160

Древплита 325 325 225 100 0 0

Анализ чувствительности оптимального решения

В процессе выполнения принятой производственной программы (плана)

ее корректировка значительно затруднена. Ведь под нее разрабатываются

календарные планы использования оборудования и производства комплектов

различных деталей мебели, сетевые графики общей последовательности работ,

сменные производственные задания и т.д. То есть, с корректировкой плана

связана необходимость изменения организации работы всего предприятия.

Внедрение новой технологии, оборудования, материалов, организации

производства не всегда может быть спланировано заранее. Однако такого рода

мероприятия выгодны предприятию, поскольку зачастую позволяют снизить

себестоимость, улучшить качество изделий, что в конечном итоге ведет к

увеличению прибыли.

Неизбежное колебание значений таких экономических параметров как

цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может

привести к неоптимальности или непригодности прежнего режима работы. Для

учета подобных ситуаций проводится анализ чувствительности оптимального

решения, т.е. выяснение того, как возможные изменения параметров исходной

модели повлияют на полученное ранее оптимальное решение.

Ограничения линейной модели для решения задачи анализа

чувствительности классифицируются следующим образом:

– связывающие ограничения, проходящие через оптимальную точку;

– несвязывающие ограничения, не проходящие через оптимальную

точку.

Ресурс, представляемый связывающим ограничением, называется

дефицитным, а ресурс, представляемый несвязывающим ограничением –

недефицитным. Ограничение называют избыточным, если его исключение не

влияет на оптимальное решение. Выделяют две задачи анализа на

чувствительность:

1. Анализ сокращения или увеличения ресурсов.

2. Анализ изменения коэффициентов ЦФ.

Методика графического анализа чувствительности

оптимального решения

Первая задача. Рассмотрим вопрос регулирования запасов ресурсов,

используемых для выполнения производственной программы. Анализ

оптимального решения позволяет сделать вывод, что связывающими

ограничениями являются ограничения 2 и 3, соответственно, дефицитными

ресурсами будут: пиломатериалы и оборудование. Согласно табл. 1.3 они

расходуются полностью и по этой причине невозможно дальнейшее

наращивание производства, т.е. если появится возможность увеличить объем

этих ресурсов, она позволит увеличить план выпуска продукции.

Чтобы графически определить максимальное увеличение объема

дефицитного ресурса, вызывающее улучшение оптимального решения,

необходимо передвигать соответствующую прямую в направлении улучшения

ЦФ до тех пор, пока это ограничение не станет избыточным (рис. 1.2).

В нашем случае при прохождении прямой 3 (оборудование) через точку В

ограничение 3 становится избыточным и возникает новый симплекс с

вершинами 0–1–2–3–В–5, в котором оптимальной будет точка В, а

связывающими ограничениями становятся 4 (древплита) и 2 (пиломатериалы).

Аналогично, увеличение объема ресурса 2 (пиломатериалы) целе-

сообразно до точки А, в которой образуется новый симплекс 0–1–А–4–5, а

связывающими ограничениями становятся 1 (ткань) и 3 (оборудование).

Правило 1. Чтобы численно определить максимальную величину запаса

дефицитного ресурса, вызывающую улучшение оптимального плана

необходимо:

1) определить координаты точки (х

; х

), в которой соответствующее

ограничение становится избыточным,

2) подставить координаты (х

; х

) в левую часть соответствующего

ограничения.

3.7x

+4x

→max

100

оборудование

3)5x

+4x

≤810

пиломатериалы

2)0.06x

+0.1x

≤14.4

ткань

1)3.3x

≤396

древплита

4)2.5x

≤325

150

250

100

≥0

Рис. 1.2

Координаты точки В (130;66) находятся путем решения системы

уравнений прямых 4 и 2. При подстановке полученных значений в левую часть

ограничения 3 получается допустимый объем ресурса оборудование равный

914. Дальнейшее увеличение не изменит симплекса и не приведет к другому

оптимальному решению. Полная прибыль в новой оптимальной точке будет

равна 745 р. Аналогично, рассчитываются: координаты точки А (66;120),

максимально допустимый объем ресурса пиломатериалы (15,96) и полная

прибыль (724 р.).

Ограничения 1 и 4 являются не связывающими, а соответствующие им

ресурсы недефицитными. С экономической точки зрения это означает, что в

данный момент объем ресурса ткань непосредственно не определяет объемы

производства. Поэтому некоторое его колебание может никак не повлиять на

оптимальный план производства в точке 3. Увеличение (уменьшение) запаса

будет соответствовать перемещению прямой ограничения 1 вверх (вниз).

Перемещение прямой 1 вниз не влияет на существующее оптимальное

решение только до пересечения с точкой 3. Дальнейшее уменьшение ведет к

образованию нового симплекса с худшим оптимальным решением. Отсюда

вывод: чтобы определить максимальное уменьшение запаса недефицитного

2,5x

≤

325

3,3x

≤396

0,06x

+0,1x

≤

14,4

3,7x

+4x

→max

ресурса необходимо передвигать соответствующую прямую до пересечения с

оптимальной точкой.

Правило 2. Чтобы численно определить минимальную величину запаса

недефицитного ресурса, необходимо подставить координаты оптимальной

точки в левую часть соответствующего ограничения.

В ограничение 1 (ткань) подставляются координаты точки 3, получается

новое значение 297 р. Аналогично проводится исследование возможного

снижения запаса древплиты.

При наличии ограничений на затраты, связанные с созданием

дополнительных запасов исходных продуктов, «лицу, принимающему решения»

(ЛПР), важно знать, какому ресурсу следует отдать предпочтение. Для этих

целей используют дополнительную характеристику – ценность

дополнительной единицы ресурса, которая определяется как отношение

максимального приращения целевой функции к максимально допустимому

приращению объема ресурса. Результаты анализа возможного сокращения

(увеличения) ресурсов представлены в табл. 1.4.

Таблица 1.4

№ ресурса

Тип ресурса Мах изменение

ресурса,

∆max

Мах изменение

прибыли,

max∆Z

Ценность дополни-

тельной единицы

ресурса,

max

∆

1 Недефицитный –99 0 0

2 Дефицитный 1,56 31 19,87

3 Дефицитный 104 52 0,5

4 Недефицитный –100 0 0

Анализируя полученные результаты, ЛПР может сделать вывод, что при

наличии средств дополнительные вложения следует направить на увеличение

объема ресурса 2, а лишь затем на увеличение ресурса 3.

Задание 3. Провести графический анализ возможности увеличения или

сокращения ресурсов при условии неизменности оптимального плана.

Результаты анализа представить в графическом виде и в виде таблицы.

Вторая задача. Рассмотрим вопрос о возможности снижения

себестоимости каждого из видов продукции при условии оптимальности

выбранного плана и неизменности цен продукции. Как отмечалось выше, угол

α прямой, соответствующий целевой функции, определяется соотношением

прибылей, а последняя равна разности оптовой отпускной цены и

себестоимости. Таким образом, если меняется себестоимость продукции, то при

неизменной цене меняется прибыль и, следовательно, угол наклона α. При этом

пределы изменения угла α, обеспечивающие оптимальность выбранного плана,

таковы, что положение прямой II (см. рис. 1.1), соответствующей критерию

оптимальности, заключено между прямыми 2–3 и 3–4, соответствующими

ограничениям на пиломатериалы и оборудование.

Изменение цен на продукцию представляется на графике вращением

прямой, соответствующей критерию эффективности, вокруг оптимальной

точки. Так при увеличении первого коэффициента целевой функции или

уменьшении второго прямая будет вращаться по часовой стрелке, иначе –

против часовой стрелки. При таких поворотах точка 3 будет оставаться

оптимальной до тех пор, пока наклон прямой II не выйдет за пределы,

определяемые наклонами прямых ограничений 2 и 3.

Итак, угол α может меняться в пределах α

≤ α ≤ α

, где α

– угол наклона

прямой, соответствующей ограничению на пиломатериалы, а α

– угол прямой,

соответствующей ограничению на оборудование. Как известно, тангенс угла

наклона прямой пропорционален углу наклона и определяется отношением ее

коэффициентов. Следовательно, в соответствии с данными задания

,925,04/7,3/tg

,25,14/5tg

,6,01,0/06,0tg

====

===

ppk

таким образом

3212

kppk

≤

. (1.12)

Подставляя числа, получим 0,6≤0,925≤1,25. Снижая себестоимость шкафа

на ∆p

, тем самым можно на ∆p

увеличить прибыль p

. Так как значение p

находится в числителе отношения, определяющего значение tgα, то увеличение

прибыли на шкаф приведет к увеличению угла наклона α прямой,

соответствующей критерию эффективности. Как следует из (1.12), предельное

увеличение значения tgα, не нарушающее условия оптимальности выбранного

плана, возможно до значения k

=1,25, т.е.

∆

(1.13)

где ∆p

= k

– p

= 1,25⋅4 – 3,7 = 1,3 р.

Следовательно, если себестоимость шкафа снизится не больше, чем на 1,3

р., то условие оптимальности выбранного плана сохраняется. В противном

случае этот план будет уже не самым лучшим (не оптимальным) по прибыли.

Если снижать себестоимость кровати на ∆p

, то tgα уменьшится.

Предельное снижение себестоимости, не нарушающее условия оптимальности

выбранного плана, составит

∆+

(1.14)

где ∆p

= p

– p

= 3,7/0,6 – 4 = 2,17 р.

Задание 4. Выполнить количественную оценку возможностей снижения

себестоимости каждого из запланированных к выпуску видов продукции при

условии неизменности оптимального плана. Определить, при каких

соотношениях прибылей найденный план перестает быть оптимальным.

Контрольные вопросы

1. Какая система уравнений называется совместной? Определенной?

Несовместной? Неопределенной?

2. С какими системами уравнений приходится иметь дело в задачах

оптимального планирования?

3. Какие системы уравнений называются эквивалентными?

4. Какие преобразования системы уравнений приводят к эквивалентной

системе?

5. Является ли умножение обоих частей уравнения на одно и то же число,

отличное от нуля, эквивалентным преобразованием?

6. Является ли прибавление к обеим частям уравнения соответствующих

частей другого уравнения, умноженных на произвольное число, эквивалентным

преобразованием?

7. Какая система уравнений называется системой с базисом?

8. Что такое базисные неизвестные (переменные)?

9. Какое решение системы уравнений называется базисным?

10. Можно ли привести совместную систему линейных уравнений к

эквивалентной системе уравнений? Если да, то как?

11. Что такое общая задача линейного программирования?

12. Что такое каноническая задача линейного программирования?

13. Что такое стандартная задача линейного программирования?

14. Что включает в себя математическая модель задачи линейного

программирования?

15. Что такое допустимое решение задачи линейного программирования?

16. Что такое оптимальное решение задачи линейного

программирования?

17. Что такое симплекс?

18. Какие задачи решаются при выполнении анализа чувствительности

решения?

19. Какие ресурсы называются дефицитными? Недефицитными?

ЛАБОРАТОРНАЯ РАБОТА № 2 (2 часа)

Тема работы: Использование табличного процессора Excel для поиска

оптимальных решений задач экономики. Формулировка и решение в Excel

задачи линейного программирования.

Содержание работы и порядок ее выполнения

Лабораторная работа включает в себя знакомство с методикой

формулировки и решения задач математического программирования с

использованием процедуры «Поиск решения» (Solver) табличного процессора

Excel, а также практическое приложение полученных знаний для решения

задачи составления оптимального по прибыли плана выпуска двух видов

мебели и рассчитана на 2 часа лабораторных занятий.

Студент на занятии знакомится с процедурой «Поиск решения»

табличного процессора Excel и использует её для формулировки и решения

задачи составления оптимального по прибыли плана выпуска двух видов

мебели по данным задания лабораторной работы №1.

После решения задачи на ЭВМ студент во внеаудиторное время

составляет отчет о порядке выполнения работы, вносит в отчет результаты

обработки данных, полученных на ЭВМ, и защищает отчет в назначенное

преподавателем время. Методические указания по составлению и оформлению

отчета о лабораторной работе изложены в конце методических указаний.

Пример постановки задачи оптимизации в Excel

Рассмотрим задачу оптимального планирования выпуска продукции

(лабораторная работа №1). Производственному участку поручено выпускать

мебель двух видов: кровати и шкафы, на производство которых выделены

сырьевые и производственные ресурсы (табл. 2.1). Требуется составить

оптимальный по прибыли план выпуска продукции.

Таблица 2.1

Затраты ресурсов на единицу продукции

Виды

продукции

Ткань

обивочная, м

Пилома–

териалы, м

Оборудование,

cтанко–смен

Древ.

плита, м

Прибыль на

единицу

продукции, р.

1. Шкаф 0 0,06 5 2,5 3,7

2. Кровать 3,3 0,1 4 0 4

Объемы

ресурсов

396 14,4 810 325

Обозначим искомое число шкафов через х

, а число кроватей – через х

Тогда математическая модель задачи запишется так

Z = 3,7x

+ 4x

→ max











≥≥

≤

≤+

≤

;0 ;0

;3255,2

;81045

;4,141,006,0

;3963,3

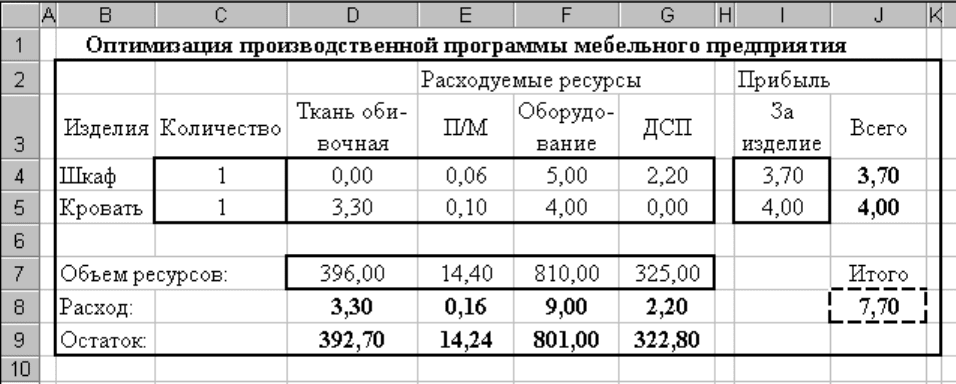
Вначале исходные данные размещаются на рабочем листе Excel, как это

показано на рисунке 2.1, каждой переменной и каждому коэффициенту задачи

ставится в соответствие конкретная ячейка (выделенная рамкой).

Ячейки С4:С5 – изменяемые ячейки, в которые записываются некоторые

начальные значения (в данном примере 1). Расход ресурсов на единицу изделия

помещен в ячейках D4:G5, объем ресурсов – в ячейках D7:G7, прибыль на

единицу изделия – в ячейках I4:I5. Ячейка J8 выбрана в качестве целевой

ячейки, содержащей формулу =СУММ(J4:J5). Она связана с изменяемыми

ячейками через ячейки J4:J5, в которых содержатся формулы: =I4*С4 и =I5*С5.

Расход ресурсов (ячейки D4:G5) связан с изменяемыми ячейками

формулами: =D4*C4+D5*C5, =E4*C4+E5*C5, =F4*C4+F5*C5 и =G4*C4+G5*C5,

помещенными во влияющие ячейки D8:G8 соответственно.

Задание 1. В соответствии с данными индивидуального задания

лабораторной работы № 1 сформировать в ячейках листа Excel шаблон решения

задачи оптимизации по прибыли плана выпуска продукции мебельного

предприятия.

Рис. 2.1

Процедура «Поиск решения» табличного процессора Excel

После внесения всех зависимостей, составляющих математическую

модель, на рабочий лист Excel для дальнейшего решения вызывается процедура

«Поиск решения», с помощью которой могут быть решены многие задачи

экономики, формулируемые как задачи математического программирования, а

именно:

– минимизация затрат на транспортировку,

– составление смеси,

– оптимальный раскрой материалов,

– оптимизация финансовых показателей,

– штатное расписание,

– максимизация выпуска товаров при

ограничениях на сырье.

Поиск решения задач математического

программирования осуществляется в Excel с

использованием команды Поиск решения... из пункта

главного меню Сервис (рис. 2.2). При этом появляется

диалоговое окно Поиск решения, показанное на рис. 2.3.

В поле Установить целевую записывается ссылка

на ячейку, содержащую формулу с целевой функцией. В группе

переключателей Равной указывается направление оптимизации ЦФ.

В поле Изменяемые ячейки указываются ячейки, изменением которых

достигается экстремальное значение целевой ячейки. Они должны содержать

какие–либо допустимые значения элементов решения оптимизационной задачи

и быть связаны формулой листа (целевой функцией), помещаемой в целевую

Рис. 2.3

Рис. 2.2