Спирин Н.А., Лавров В.В. Информационные системы в металлургии

Подождите немного. Документ загружается.

Глава 7. Интеллектуальные системы

7-13

Глава 7. Интеллектуальные системы

7-14

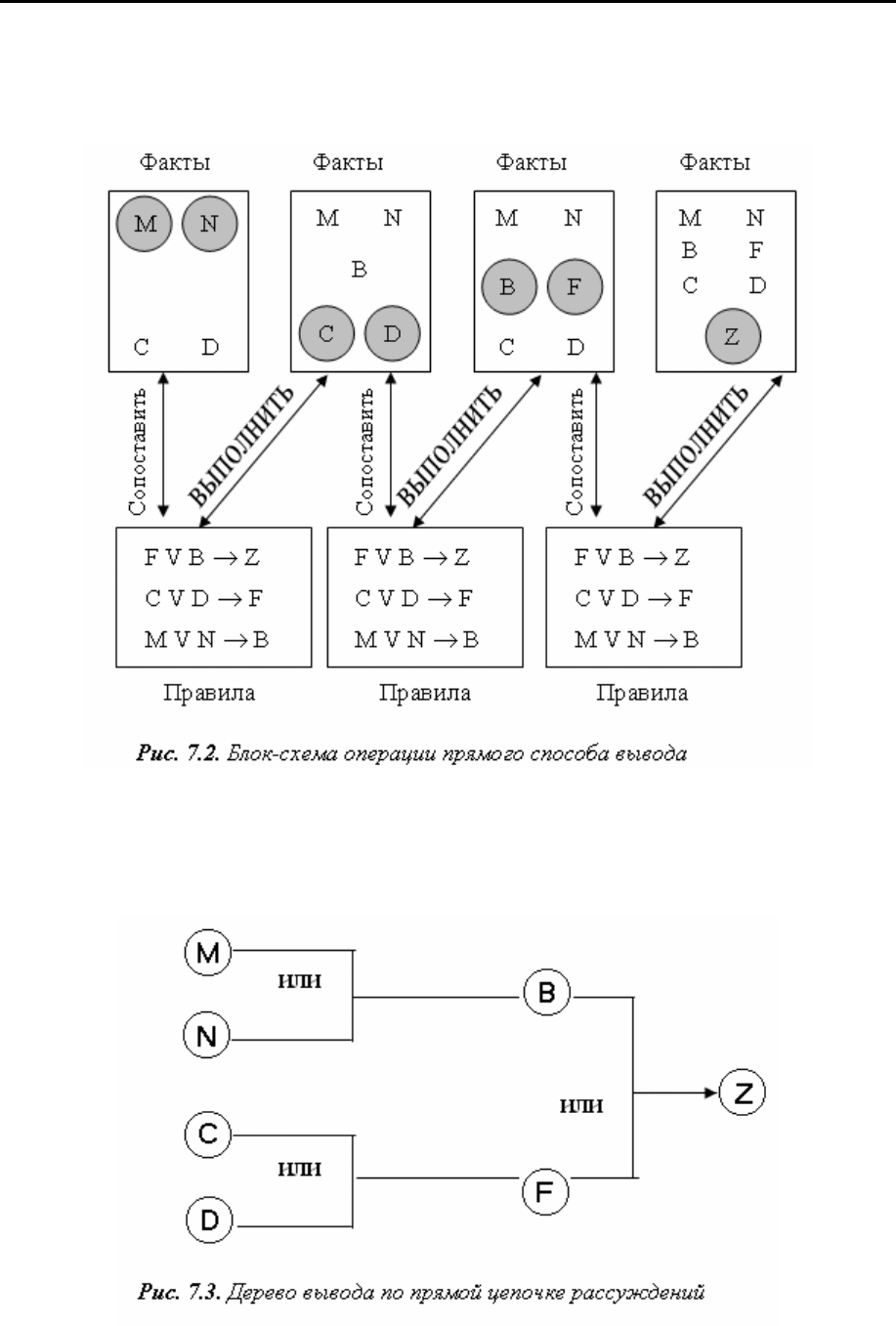
Предположим, что не удалось получить заданную марку стали в кисло-

родном конвертере. В чем дело – неправильно был определен расход кислорода

или неправильно выбран расход флюсов? Рассмотрим ту же задачу, что и при

прямой цепочке рассуждений. По известному результату необходимо опреде-

лить условия, которые к нему привели, т.е. по симптомам найти

причины. Она

отличается от предыдущей задачи тем, что там уже были известны условия (M,

N, C, D), но последствия Z, к которым они приведут, известны не были.

На рис. 7.4 показано, как обратная цепочка рассуждений должна рабо-

тать, используя правила из примера прямой цепочки рассуждений.

На первом шаге системе говорится, чтобы она установила (если

может),

что ситуация Z существует. Сначала она проверит базу в поисках Z, и в случае

неудачи, будет искать среди правил то, которое приводит к установлению факта

Z, т.е. правило, у которого Z стоит справа от стрелки. Она находит правило F∨B

→ Z и решает, что должна установить факты F и

B, чтобы вывести Z.

На втором шаге система пытается установить факт F, сначала проверяя

базу данных, а затем ищет правило, в правой части которого стоит F. Из этого

правила C∨D → F система решает, что должна установить существование фак-

тов С и D для получения заключения о F.

На шагах с

третьего по пятый система находит С и D в базе и устанавли-

вает факт существования F, но решает, что она должна установить факт B, пре-

жде чем она получит заключение о Z.

На шагах с шестого по девятый система находит М и N в базе и устанав-

ливает факт существования B и, наконец

, на десятом шаге выполняет первое

правило, чтобы установить основную цель – факт существования Z.

Цепочка выводов, созданная здесь, идентична той, что была создана в ре-

зультате прямой цепочки рассуждений. Отличие этих подходов заключается в

способе поиска правила и данных, здесь идет поиск и среди правил, и среди

данных.

7.4.2. Логические модели

представления знаний

Логические модели представления знаний отображают знания данной

предметной области в виде совокупности простых фактов, утверждений и суж-

дений.

Факты отображаются в виде базовых элементов некоторой формальной

системы. Утверждения и суждения отображаются в виде формул, которые со-

ставляются из базовых элементов с использованием синтаксических и семанти-

ческих правил.

Любая

формальная логическая система, отображающая знания, задается

совокупностью множеств:

L = <T,S,A,P>,

Глава 7. Интеллектуальные системы

7-15

Глава 7. Интеллектуальные системы

7-16

где T – множество базовых элементов (символов, букв, слов);

S – множество синтаксических правил, позволяющих строить из Т син-

таксически правильные выражения или формулы;

А – множество априорно истинных выражений, называемых аксиомами;

Р – семантические правила, или правила вывода, позволяющие расши-

рять множество аксиом А за счет новых формул, которые также являются ис-

тинными в

данной формальной системе.

Логические модели представления знаний предполагают, что область

или задача описывается в виде набора аксиом.

Для разработки логических моделей представления знаний используют

исчисление высказываний и исчисление предикатов.

Исчисление высказываний

Исчисление высказываний рассматривает высказывания, или утвержде-

ния, которые могут быть либо истинными, либо ложными. Например, высказы-

вание «Увеличение

температуры греющей среды повышает плотность теплового

потока на поверхность нагреваемого тела – научный факт, который всегда явля-

ется истинным». Каждое простое высказывание можно записать в следующей

символической форме, или нотации:

А = «насос увеличивает давление жидкости»; В = «теплообменник при-

меняют для передачи теплоты» (где А и В – истинные простые высказывания,

или атомы

Для представления сложных высказываний, или формул, необходимо

простые высказывания объединить с использованием логических связок.

С этой целью по аналогии с образованием составных высказываний в ре-

чи в логике высказываний вводятся следующие операции над высказываниями.

Отрицание – унарная операция, соответствует употреблению частицы

«не», для обозначения которой используют знак

⎤ , not, (не,).

Конъюнкция

– бинарная операция, соответствующая употреблению сою-

за «и».

∧, &, and (и).

Условие истинности для конъюнкции A∧B заключается в том, что А ис-

тинно и В истинно.

Дизъюнкция – бинарная операция, соответствующая употреблению

союза «или».

∨, or (или).

Условие истинности для дизъюнкции A∨B заключается в том, что А ис-

тинно или В

истинно.

Импликация – бинарная операция, близкая по смыслу к союзу «ес-

ли...то ...».

→ (если...то...).

Условие истинности для импликации A→B заключается в том, что если

А истинно, то В истинно. Высказывание А в импликации A→B читается «А им-

Глава 7. Интеллектуальные системы

7-17

плицирует В» или «из А следует В». Высказывание A→B ложно только в одном

случае, когда А истинно, а В ложно.

Эквивалентность – бинарная операция, обозначается знаком

↔ (тогда, когда).

Высказывание А↔В истинно только тогда, когда А и В оба истинны ли-

бо оба ложны.

Скобки ().

Рассмотрим запись в

символической форме сложного высказывания:

Е = « В технологическую схему входят нагревательные печи и прокат-

ный стан». Имеются два простых истинных высказывания: С = «В технологиче-

скую схему входят нагревательные печи»; D = «В технологическую схему вхо-

дит прокатный стан».

Сложное высказывание Е представляет собой конъюнкцию, т.е.

Е↔(С∧ D).

Сложное высказывание

Н = «Жидкую сталь можно разлить как в излож-

ницы, так и на машине непрерывного литья заготовок» представляет собой

дизъюнкцию двух простых высказываний: М = «Жидкую сталь можно разлить в

изложницы», Р = « Жидкую сталь можно разлить на машине непрерывного ли-

тья заготовок», т.е.

Н ↔ М∨Р.

В сложном высказывании

М = «Если в полупродукте содержатся желе-

зосодержащие частицы, то их можно отделить от пустой породы методом маг-

нитного обогащения» выделим три простых высказывания:

Р = «полупродукт содержит железосодержащие элементы»;

Q = «полупродукт поступает на магнитное обогащение»;

N = «железосодержащие элементы отделяются от пустой породы».

Тогда сложное высказывание М можно представить как импликацию:

Если (полупродукт содержит железосодержащие частицы) и (пустую породу),

то (железосодержащие частицы отделяются от пустой породы)»:

М ↔[(Р∧Q) →N].

Исчисление предикатов

Исчисление предикатов является расширением классического исчисле-

ния высказываний, в котором каждое высказывание рассматривается как единое

целое, не обладающее внутренней структурой, а истинность и ложность формул

и атомов

фиксированы.

В исчислении предикатов основным элементом является предикат – пе-

ременное высказывание, то есть логическая функция

Р(x

, x

,… x

истинность или ложность которого зависит от значения входящих в пре-

дикат предметных переменных, или аргументов x

, x

,… x

Обратим ваше внимание на то, что предикат Р принимает значение “ис-

тина” или “ ложь в зависимости от того, какие значения принимают входящие в

него переменные x

, x

,… x

Глава 7. Интеллектуальные системы

7-18

Порядок следования аргументов должен всегда задаваться в соответст-

вии с интерпретацией предиката, принятой для моделирования предметной об-

ласти при разработке информационной системы, т.е. разработчик должен при-

нять решение о фиксированном, приемлемом для интерпретации порядке и не-

укоснительно соблюдать его в системе при работе с такими данными.

Например, факт “В доменную

печь вдувается горячее дутье” можно

представить следующим образом:

Вдувание (доменная печь, дутье).

Причем теперь в системе все предикаты такого типа должны в списке ар-

гументов на первом месте содержать тип печи, а на втором месте – вид вдувае-

мого вещества.

Вдувание (мартеновская печь, кислород).

Вдувание (методическая печь, природный газ) и

т.п.

Высказывания, состоящие из предиката и связанных с ним аргументов,

называются элементарными. Элементарные высказывания могут объединяться

в сложные высказывания с помощью логических связок.

Действительно, вследствие того, что предикаты являются двоичными

(логическими) переменными, над ними можно производить логические опера-

ции. Рассмотрим выражение

)∧ P

))∨ (P

)∧⎤ P

)).

Его можно рассматривать как составную формулу алгебры логики, кото-

рая является функцией четырех логических переменных P

, x

), P

, x

), P

, x

), P

). Заметим, что P

, x

), P

, x

) зависят от разных перемен-

ных и, следовательно, определяют разные логические функции.

Это же выражение можно рассматривать и как составной трехместный

предикат P

, x

). Ведь в зависимости от значений предметных переменных

, x

предикаты, входящие в выражение, будут принимать значения «истина»

или «ложь», а следовательно, и значение этого выражения будет зависеть от зна-

чений этих трех переменных.

Для того чтобы в исчислении предикатов можно было манипулировать

переменными, введены дополнительные структуры – кванторы.

Кванторы служат для указания меры, в какой экземпляры переменных

должны быть истинны

, чтобы высказывание в целом тоже было истинным.

Кванторы употребляют только с предметными переменными.

∈ – квантор общности («для всех»);

∃ – квантор единственности («существует такой»).

Например, пользуясь кванторами, предложение “все студенты-

дипломники знают теорию горения” можно представить следующим образом:

(∈Х) (студенты-дипломники (Х) →теория горения (Х)),

а предложение “некоторые студенты-дипломники

будут работать по специаль-

ности” можно представить следующим образом:

(∃Х) (студенты-дипломники (Х) → работать по специальности (Х)).

Пользуясь кванторами, предложение “все пламенные печи имеют топли-

восжигающие устройства” можно представить следующим образом:

(∈Х) (пламенные печи (Х) → топливосжигающие устройства (Х)),

Глава 7. Интеллектуальные системы

7-19

а предложение “в некоторые доменные печи вдувается пылеугольное топливо” в

виде

(∃Х) (доменные печи (Х) → пылеугольное топливо (Х)).

Кванторы общности и кванторы существования могут перемежаться в

пределах одного и того же выражения. В этом случае порядок, в соответствии с

которыми вводятся квантифицируемые переменные, может влиять на смысл вы-

сказывания

. Например, утверждение

(∈Х) (∃Y) (Служащий (Х) →Руководит (Y, Х))

может быть интерпретировано как “каждым служащим Х руководит некоторое

лицо Y”.

Логическое выражение

(∃Y) (∈Х) (Служащий (Х) →Руководит (Y, Х))

соответствует утверждению “есть такое лицо Y, которое руководит всеми Х”.

Для закрепления материала приведем примеры с использованием исчис-

ления

высказываний и исчисления предикатов. Применяя исчисления высказы-

ваний, запишем некоторые факты, представленные фразами предметной облас-

ти.

«Реакция экзотермическая»: (Реакция – экзотермическая).

«Реактор адиабатический»: (Реактор – адиабатический).

«Реактор изотермический»: (Реактор – изотермический).

«Реакция не экзотермическая»: (Реакция – ⎤ экзотермическая).

«Реакция экзотермическая и реактор адиабатический»:

(Реакция экзотермическая) ∧ (Реактор адиабатический).

Однако исчисление высказываний

обладает рядом ограничений для вы-

ражений сложных утверждений. Например, используя только исчисление выска-

зываний, необходимо написать такие формулы и фразы естественного языка:

Реакция – А -экзотермическая: «Реакция – А –экзотермическая»;

Реакция – В – экзотермическая: «Реакция – В – экзотермическая» и т.д.

для каждой экзотермической реакции.

Вместо этого, используя исчисление предикатов, можно написать сле-

дующие выражения:

Экзотермическая (х), где х – предметная переменная, имеющая значе-

ния: Реакция – А, Реакция – В и т.д.

Таким образом, можно представить все экзотермические реакции наибо-

лее простой моделью.

Простой факт, что “Для каждой экзотермической реакции имеет место

любой адиабатический реактор, реактор не может быть изотермическим” можно

представить в виде формальной

записи исчисления предикатов:

(∈Х) (Экзотермическая (Х)∧ (∃Y) (Адиабатический (Y)) →

⎤ (Изотермический (Y)).

7.4.3. Представление знаний с использованием

семантических сетей

Глава 7. Интеллектуальные системы

7-20

Термин семантическая означает смысловая, а сама семантика – это нау-

ка, устанавливающая отношения между символами и объектами, которые они

обозначают, т.е. наука, определяющая смысл знаков. Термин семантическая

сеть применяется для описания метода представления знаний, основанного на

сетевой структуре.

Семантические сети были первоначально разработаны для использова-

ния их в качестве психологической модели

человеческой памяти. Теперь это

стандартный метод представления знаний в экспертных системах.

Основная идея способов представления знаний на основе аппарата се-

мантических сетей состоит в рассмотрении проблемной области (а точнее, ее

модели) как совокупности объектов и отношений между ними.

Объекты при таком подходе представляются именованными вершинами,

а связи – направленными именованными дугами

некоторой семантической сети.

Тогда система знаний представляется некоторой семантической сетью (ориенти-

рованным графом, образованным именованными вершинами и дугами или их

совокупностью).

В качестве вершин семантической сети выступают только те объекты

проблемной области, которые необходимы для решения поставленных задач. В

качестве таких объектов могут выступать понятия, события, процессы и т.д.

Знания

можно описывать отношениями между абстрагированными поня-

тиями и сущностями, являющимися конкретными объектами реального мира.

Понятия и отношения между ними можно описать сетью, состоящей из узлов и

дуг. Узлы в такой сети выражают сущности и понятия, а дуги могут быть снаб-

жены метками, которые показывают, что именно они описывают.

Таким образом,

семантическая сеть – это ориентированный граф, верши-

ны которого – понятия, а дуги – отношения между ними.

Проблема поиска решения на базе знаний типа семантической сети сво-

дится к задаче поиска фрагмента сети в виде некоторой подсети, соответствую-

щей поставленному вопросу.

Проиллюстрируем использование семантической сети в качестве проце-

дуры поиска решений неформализованных задач.

Общая

методика решения неформализованных задач основана на ис-

пользовании принципа многоуровневой декомпозиции исходной задачи.

Сущность принципа многоуровневой декомпозиции при поиске решения

состоит в том, что решение исходной задачи – Р

сводится к поиску решений

образующих ее задач меньшей размерности – Р

, Р

, ...., Р

, в целом представ-

ляющих всю задачу. Процедуру декомпозиции повторяют для каждой подзадачи

до тех пор, пока каждая из полученного набора подзадач, образующих решение

исходной задачи, не будет иметь очевидное, или тривиальное решение.

Процедуру поиска исходной неформализованной задачи декомпозицией

ее на подзадачи можно представить в виде семантического графа – дерева де-

композиции

исходной задачи, называемого «И/ИЛИ» («AND/OR») графом. Ка-

ждой вершине этого графа ставится в соответствие описание некоторой задачи

(подзадачи).

В графе выделяют два типа вершин:

Глава 7. Интеллектуальные системы

7-21

• вершины типа «И (AND)»;

• вершины типа «ИЛИ (OR)».

Для «И»-вершины решение задачи сводится к решению всех подзадач, соответ-

ствующих ее вершинам-потомкам. Для «ИЛИ»-вершины решение задачи сво-

дится к решению любой из подзадач, соответствующих ее вершинам-потомкам.

Во множестве вершин «И/ИЛИ» графа выделяют одну начальную вершину

(вершину

-корень), т.е. задачу, которую следует решить, и подмножество вися-

чих конечных (целевых) вершин, т.е. заведомо разрешимых задач.

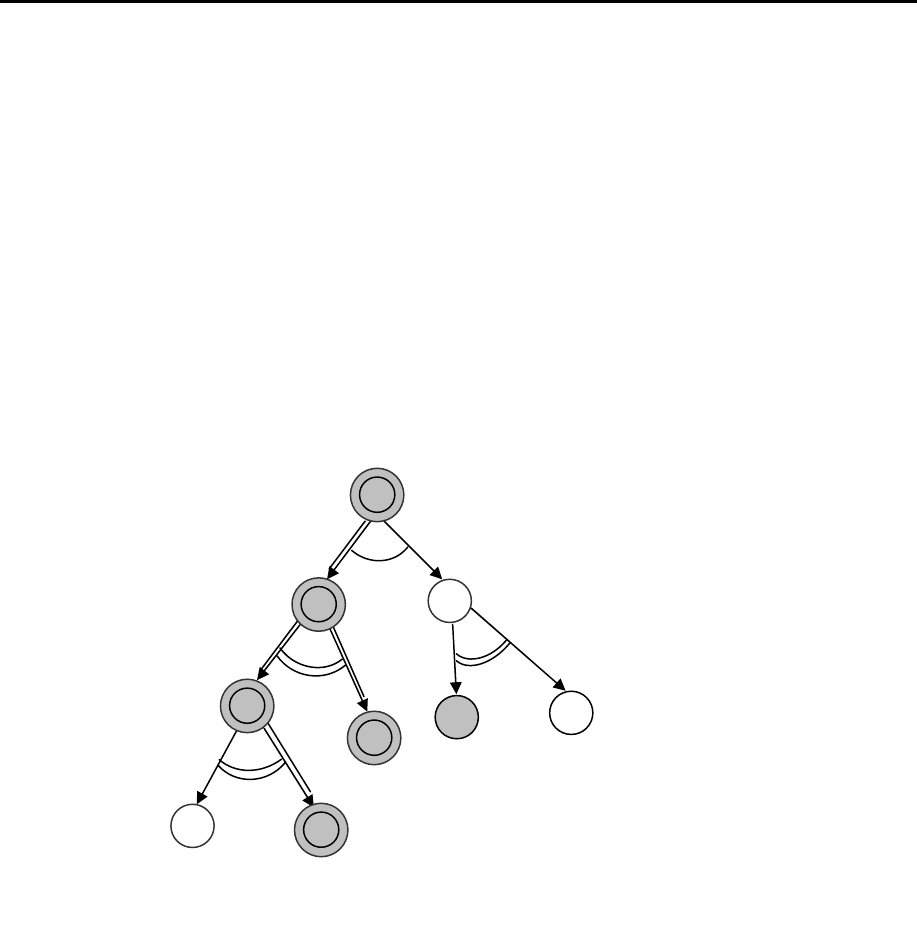
Пример дерева декомпозиции исходной НФЗ на подзадачи приведен на

рис. 7.5. Здесь Р

– исходная задача, для решения которой требуется решить или

подзадачу Р

, или подзадачу Р

. Решение подзадачи Р

сводится к решению под-

задач Р

и Р

, в свою очередь решение подзадачи Р

возможно при наличии Р

или Р

. Решение подзадачи Р

сводится к решению подзадач

и Р

. Решение за-

дач Р

, Р

предполагается известным, а Р

и Р

неизвестным.

или

Рис. 7.5. Дерево декомпозиции и решающий граф «и/или»

Цель процедуры поиска решения в «И/ИЛИ» графе – показать, что на-

чальная вершина разрешима, т.е. для этой вершины существует решающий под-

граф.

Определение разрешимой вершины в «И/ИЛИ» графе можно сформули-

ровать следующим образом:

1) конечные (целевые) вершины разрешимы, так как решение известно

по исходному предположению;

2) «

ИЛИ» – вершина разрешима тогда и только тогда, когда разрешима

хотя бы одна из ее вершин-потомков;

3) «И» – вершина разрешима тогда и только тогда, когда разрешимы все

ее вершины – потомки.

Таким образом, решающий подграф «И/ИЛИ» графа – это подграф из

разрешимых вершин, который показывает, что начальная вершина разрешима в

соответствии

с приведенным выше определением. На рис. 7.5 разрешимые вер-

Глава 7. Интеллектуальные системы

7-22

шины заштрихованы, а неразрешимые не заштрихованы, двойными линиями

выделен решающий подграф задачи Р

Для некоторой подзадачи могут быть неизвестны ни ее решения, ни спо-

соб сведения ее к более простым подзадачам. Такую подзадачу называют нераз-

решимой. Определение неразрешимой вершины в «И/ИЛИ» подграфе можно

сформулировать следующим образом:

1) вершины, не являющиеся конечными и не имеющие вершин-

потомков, неразрешимы;

2) «ИЛИ» – вершина неразрешима тогда

и только тогда, когда неразре-

шима каждая из ее вершин-потомков;

3) «И» – вершина неразрешима тогда и только тогда, когда неразрешима

хотя бы одна из ее вершин-потомков.

В общем случае процедуру решения можно представить в виде графа

G=(X,Y), где X={x

, x

,...} – множество (в общем случае бесконечное) вершин

графа, каждая из которых отображает одно из состояний; Y – множество дуг,

инцидентных паре вершин (x

, x

); x

, x

∈Χ.

Множество дуг, исходящих из вершины x

, отображает множество опе-

раторов, которые могут быть применимы к состоянию, отображаемому верши-

ной x

. В множестве вершин Х выделяют подмножество вершин Х

⊆Х, отобра-

жающее множество начальных состояний (S

), и подмножество вершин X

⊆Х,

отображающее множество конечных (целевых) состояний (S

). Множество Х

может быть задано как явно, так и неявно, т.е. через свойства, которыми должны

обладать целевые состояния. Очевидно, что решение неформализованных задач

методом поиска в пространстве состояний сводится к процедуре поиска пути L в

графе G. Путь из х

∈Х

в x

⊂Χ

называют решающим (целевым). Построение

пространства осуществляется с помощью следующей операции. К некоторой

вершине из х

∈Х

применяют все возможные операции, порождающие все ее

вершины-потомки. Порождение всех вершин-потомков для некоторой вершины

называют операцией раскрытия вершин. Если получена целевая вершина, то

она не раскрывается. Операция построения пространства состояний заканчива-

ется, когда все нераскрытые вершины являются целевыми.

Для поиска решений на «И/ИЛИ» графе необходимо обеспечить полноту

поиска, т.е. организовать поиск так, чтобы все целевые вершины были найдены,

если они существуют. Надежным

способом обеспечения полноты является пол-

ный упорядоченный перебор всех вершин графа. Для каждой операции упорядо-

ченного перебора необходимо определить порядок, в котором будут перебирать-

ся вершины графа. Обычно выделяют два основных способа перебора вершин:

поиск «в глубину» и поиск «в ширину» (рис. 7.6). При поиске «в глубину» рас-

крывается та вершина,

которая была построена самой последней, а при поиске

«в ширину» вершины раскрываются в том же порядке, в котором порождаются.

Поиск «в глубину» и «в ширину» называют рутинным, или слепым поиском, по-

скольку при этом порядок раскрытия вершин предопределен и не зависит от

расположения цели. При увеличении пространства поиска способы слепого

по-

иска требуют чрезмерных затрат времени и/или памяти компьютера. Для сокра-

щения времени поиска применяют эвристические методы поиска, т.е. методы,