Сологаев В.И. Прогнозы и моделирование подтопления и дренирования в городском строительстве

Подождите немного. Документ загружается.

221

собрать, проверить и запустить на счет. Полученные результаты

обработать и осмыслить.

Моделирование с помощью МКР-Excel может производиться в

оперативных системах Windows 3.1/95/98/Me/2000 и более поздних. Таб-

лицы Microsoft Excel имеют массовое распространение. Они снабжены

встроенным языком макропрограммирования Visual Basic for Application

(VBA). Пакет Excel с помощью VBA можно настраивать на автоматиче-

скую совместную работу с другими программными продуктами, например

с картографическим пакетом Surfer. Это обеспечивается новой информа-

ционной технологией OLE Automation (ActiveX).

МКР-Excel наследует все основные полезные качества упомянутых

программных систем [317]: доступность, завершенность, коммуникатив-

ность, модифицируемость, надежность, независимость от устройств, ори-

ентированность на человека, полнота функций, понимаемость, расширяе-

мость, согласованность, тестируемость, точность, удобство переноса,

удобство поддержания, устойчивость. Специализированные коммерческие

пакеты по моделированию не полностью отвечают перечисленным крите-

рием качества (метрикам), поэтому автор рекомендует к широкому ис-

пользованию МКР-Excel — разновидность МЭТ.

Акцент при моделировании в нашей работе сделан на фильтрацию во-

ды, так как это наиболее полно отвечает теме работы по защите от подтоп-

ления в городском строительстве. Формулы моделирования для других

процессов (фильтрация воздуха, фильтрационная консолидация, влаготеп-

лоперенос, электроосмос) приведены по мере необходимости при изучении

конкретных методов борьбы с подтоплением.

Из предшествующих работ наиболее близкими по идейному содержа-

нию к нашей являются справочник Д.Ю. Панова [184] и книги Г.Н.

Каменского, И.К. Гавич, Н.А. Мясниковой и С.М. Семеновой [87; 54]. В

них формулы моделирования приведены в такой же форме записи, как и у

222

нас, то есть относительно последующего значения искомой величины (в

явном виде). В середине XX века это было очень удобно для гидрогеоло-

гов и гидротехников при моделировании с помощью ручных подсчетов.

Однако набор опубликованных формул у предшествующих авторов не так

велик. В нашей работе формулы выведены обобщенно, что позволяет пе-

реходить к частным случаям моделирования с единой методикой. Набор

формул достаточно полный для большинства практических задач по борь-

бе с подтоплением в городском строительстве.

В более поздних публикациях подавляющее большинство авторов от-

казались от непосредственной формы записи формул моделирования в свя-

зи с работой на больших ЭВМ и персональных компьютерах. Это можно

объяснить тем, что в процессе программирования моделей приходилось

применять матричную алгебру, где уравнения для моделирования удобнее

записывать в форме разностей, то есть в большинстве случаев неявно от-

носительно искомых величин (неявные схемы).

В МКР-Excel произведен возврат к первоначальной точке зрения.

Большинство формул моделирования записаны в явном виде относительно

искомой величины. Это позволяет снять с пользователя методики обреме-

нительный груз дополнительного изучения математических правил мат-

ричных операций и сосредоточить усилия непосредственно на получение

модельных результатов по защите от подтопления.

Известно, что явные схемы при нестационарном моделировании имеют

преимущество перед неявными в задачах с двумя и более пространствен-

ными переменными [24, с. 199; 86, с. 391]. Это послужило дополнитель-

ным аргументом к преимущественному использованию явных схем. Одна-

ко и неявные схемы тоже реализованы в МКР-Excel с помощью метода

прогонки. Они неплохо работают в одномерных задачах.

В последующих параграфах данной главы приводится сводка формул

моделирования. Особое внимание уделено одно- и двухмерным формулам

223

в нелинейной гидравлической постановке по Буссинеску, так как такие за-

дачи почти не решаются аналитически (за редкими исключениями, что

рассмотрено в п. 3.3, 3.4). Невозможно создать совершенно универсальные

формулы моделирования. Подборка формул отвечает научным интересам

автора и теме представленной работы.

Основные сведения по формулам моделирования изложены в п. 4.5, где

дана расширенная классификация формул моделирования и показан

способ вывода формул с постановкой исходных балансовых уравнений по

А.А. Самарскому [222; 223; 284].

Технология моделирования фильтрации при защите от подтопления в

городском строительстве аналогична технологии фильтрационных расче-

тов, которая изложена в п. 3.1 и проиллюстрирована на рис. 8 и рис. 9.

Также как и при аналитических расчетах, при моделировании вначале

нужно получить прогноз подтопления. Затем можно построить модель за-

щитного мероприятия, если по результатам прогноза защита от подтопле-

ния необходима. Технология моделирования обеспечивает более точные

результаты.

4.3. Выбор и построение модельной сетки

В начале моделирования рекомендуется проделать аналитические рас-

четы по известным зависимостям. Это позволит получить первоначальное

представление о поведении объекта защиты от подтопления. В ходе расче-

тов приходится схематизировать изучаемую область фильтрации. Приня-

тая схема в дальнейшем может служить отправной точкой при выборе

МКР-сетки.

Компьютерные модели, также как и расчеты, лучше разрабатывать в

направлении от простых к сложным. Нет смысла браться с первого раза за

трехмерную модель, утяжеленную различными особенностями. Лучше на-

224

чать с одномерной, проследить поведение объекта и по мере необходимо-

сти усложнить. Точно также не следует сразу мельчить сетку модели. На-

чинать моделировать надо с минимальным и достаточным числом узлов

сетки.

Д.Ю. Панов [184, с. 42] рекомендует первую модель собирать с мини-

мальным числом шагов сетки не менее двух пространственных шагов, то

есть не менее трех узлов-ячеек по каждой стороне моделируемой области.

Эта рекомендация совершенно правильная. Она проверена нами [254] при

моделировании верховодки на слабопроницаемой линзе. Этот прием при-

веден в [262] (пример 56). После реализации грубой модели можно из-

мельчить сетку и получить более точное решение.

При моделировании с помощью МКР-Excel по горизонтальной (в

плоскости таблицы) координатной оси максимальное число узлов с учетом

ячейки с координатой лучше задавать не более 255, что связано с количе-

ством ячеек Excel в строке, равным 256. Однако число 256 не является

пределом для горизонтальной оси, так как матрицу модели можно про-

длить ниже в таблице Excel. По вертикали, начиная с таблиц версии Excel

97 максимальное число строк равно 65536. Таким образом, в Excel можно

создавать малые, средний и даже большие МКР-модели. Возможности мо-

делирования возрастают с увеличением производительности компьютера,

что зависит от вида процессора, количества оперативной памяти, возмож-

ностей видеокарты, шины передачи данных, тактовой частоты и т.д.

Как показала практика нашего моделирования, для быстрых и эффек-

тивных исследований весьма удобны модели с числом шагов 10–50 по ка-

ждой координате. Это позволяет создавать модели, которые рассчитыва-

ются весьма быстро, за секунды—минуты.

Начинать моделировать рекомендуется с одномерных задач, чтобы хо-

рошо отработать технологию моделирования. При выборе такой модели в

первую очередь следует определить, какой системе координат ближе всего

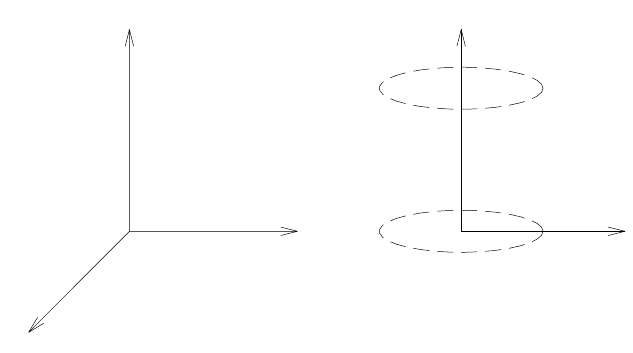
225

соответствует процесс фильтрации. Основные системы координат, приме-

няемые в теории фильтрации при защите от подтопления являются декар-

това (рис. 66а) и цилиндрическая (рис. 66б). Например, подавляющее

большинство аналитических зависимостей в справочном пособии к СНиП

[204] решены именно в этих двух системах.

Рис. 66. Системы координат: а — декартова (трехмерная); б — цилиндрическая (двух-

мерная)

Осью z в обоих системах координат обозначают вертикальную ось.

Одномерные горизонтальные задачи в декартовой системе принято совме-

щать с осью x. В цилиндрической системе координатой r обозначают не

точку, а цилиндрическую поверхность радиусом r.

Вытянутые в плане объекты, например траншеи или реки с прямым

руслом, принимают фильтрующиеся в них воды преимущественно с двух

сторон. Поэтому проводят поперечный разрез по линии течения, с которым

совмещают горизонтальную ось x декартовой системы координат. Такие

простейшие одномерные модели были рассмотрены в [262] (примеры 54 и

58), где была использована декартова система координат. Такой вид тече-

ния по горизонтали называют плоскопараллельной фильтрацией [148, с.

98].

Если фильтрация зависит от двух пространственных декартовых коор-

динат, то возможны два случая:

а) б)

226

1) плановая фильтрация, когда течение подземных вод происходит

преимущественно по горизонтали; оси координат тогда называют x и y;

2) профильная (или плоская) фильтрация, при движении в вертикаль-

ной плоскости; оси координат соответственно обозначают как х и z (верти-

кальная);

Модели плановой фильтрации обычно связаны с достаточно крупными

объектами (см. пример 56 в [262]). Профильная же фильтрация чаще всего

применяется для изучения локальных случаев фильтрации, например для

моделирования шпунтовых ограждений котлованов.

Приведем рекомендации по назначению пространственного шага сет-

ки. Сетки с равномерным шагом рекомендуют многие руководства по чис-

ленному моделированию [20; 69; 135; 184; 222]. Это упрощает формулы

моделирования и вычислительный процесс. Разбиение модели равными

шагами показано в [262] (примеры 54, 56, 58).

На одномерных горизонтальных моделях мы обозначаем равномерный

пространственный шаг в декартовых координатах DL или Dx, а в

радиальных моделях — Dr (цилиндрическая координата).

Для двухмерных моделей мы применяем следующие обозначения рав-

номерного пространственного шага:

— в декартовых координатах при квадратных МКР-сетках DL, при

прямоугольных сетках плановых моделей Dx и Dy и профильных как Dx и

Dz (по вертикали);

— в цилиндрических координатах профильно-радиальных моделей

как Dr и Dz (по вертикали).

На трехмерных моделях, которые собираем только в декартовых коор-

динатах, обозначаем равномерные пространственные шаги МКР-сетки как

Dx, Dy и Dz (по вертикали).

Иногда удобнее использовать переменный пространственный шаг. Эти

случаи обычно возникают на плановых моделях [209], а также радиальных

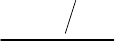
227

и профильно-радиальных [127; 289].

В книгах [76, с. 85; 127, c. 192] приведена формула Р. Столлмена [350]

для определения последующей радиальной координаты МКР-узла r

i+1

че-

рез предыдущую координату r

i+1

, что можно записать в виде

( 253)

Более удобной является формула В.С. Усенко [289, с. 168] при

разбиении неравномерной сетки в цилиндрических координатах для

определения последующей радиальной координаты МКР-узла r

i+1

через

предыдущую координату r

i+1

, которую мы тоже записываем по своему так:

( 254)

где R — максимальный радиус круговой области фильтрации, например

радиус влияния скважины до контура питания; r

— минимальный радиус

круговой области фильтрации, например радиус скважины; N

— общее

число неравномерных шагов, на которые надо разбить область фильтрации

по радиальной координате r (см. пример 57 в [262]).

В ходе исследований при моделировании нестационарных нелинейных

процессов фильтрации грунтовых вод малой мощности мы обнаружили,

что в этом случае также целесообразно использовать переменный про-

странственный шаг по формуле ( 254) не только для осесимметричных

процессов, но и для плоскопараллельных. Малый начальный шаг надо на-

значать около источника возмущения (траншеи с водоотливом, водопони-

жением или вытянутого в плане очага инфильтрации).

4.4. Критерии устойчивости нестационарных моделей

При расчете нестационарных моделей с помощью МКР-Excel мы реко-

мендуем формулы моделирования так называемого явного вида или по яв-





exp ,

i i

R r

r r



 



 

 

i+1

= r

·10

0,25

228

ной конечно-разностной схеме [86, с. 301]. Из теории и практики модели-

рования методом конечных разностей известно [20; 48; 123; 148; 164; 174;

209; 222; 223; 284], что перед расчетом таких моделей надо определенным

образом подобрать соотношение пространственных и временных шагов.

Это необходимо для обеспечения устойчивости расчета.

Критерии устойчивости нестационарных моделей приводим по указан-

ным литературным источникам, а также по результатам нашей практики

моделирования фильтрации с помощью МКР-Excel. Они даны для модели-

рования фильтрации подземных вод, так как это основной изучаемый фи-

зический процесс при защите от подтопления в городском строительстве.

Критерии устойчивости для других процессов (фильтрация воздуха,

фильтрационная консолидация, влаготеплоперенос, электроосмос) можно

принять по аналогии, переосмысливая их соответствующим образом.

Критерии устойчивости нестационарных МКР-моделей даны для одно,

двух- и трехмерных процессов фильтрации воды. Они выражены относи-

тельно максимально возможного шага времени Dt

max

на модели. Шаг вре-

мени на модели Dt в принятых единицах измерения (обычно в сутках) на-

до назначить так, чтобы он был равен или меньше величины Dt

max

. Если

шаг времени Dt = Dt

max

, то формулы моделирования упрощаются, что по-

казано в [262] (пример 58). Однако при этом величина Dt = Dt

max

может

оказаться не круглой, например не в целых сутках, как в [262] (пример 58),

когда получилось Dt

max

= 46,875 сут. В таком случае шаг времени можно

принять в целых числах, соблюдая условие Dt < Dt

max

, а формулы моде-

лирования будут без упрощения. При построении конкретной модели ис-

следователю надо самому выбрать шаг времени Dt

max

или Dt < Dt

max

Следует заметить, что при Dt < Dt

max

начальные шаги расчета будут про-

исходить более гладко, чем при Dt

max

. При дальнейших шагах времени

моделируемые процессы динамики подземных вод происходят достаточно

гладко в любом случае, то есть начальные неровности как бы «забывают-

229

ся».

Нельзя для явных МКР-схем назначать Dt > Dt

max

, иначе счет модели

станет неустойчивым и произойдет переполнение ячеек Excel недопустимо

большими числами. В таком случае в ячейке Excel появляется сообщение

#ЧИСЛО!

о недопустимом для компьютера большом числе, выходящем из диапазона

его возможностей. Например, в версии Excel 97 числа не должны выходить

из диапазона от –1·10

307

до 1·10

307

Для одномерных плоскопараллельных и радиальных МКР-моделей

критерий устойчивости при выборе шага времени такой [86, с. 390]:

( 255)

где DL

min

— минимальный пространственный шаг из принятых на модели,

для плоскопараллельных DL

min

= Dx

min

и радиальных DL

min

= Dr

min

(см.

пример 57 в [262]); а

max

— максимальная пьезопроводность (для

напорного пласта) или максимальная уровнепроводность (для

безнапорного пласта); k

max

— максимальный коэффициент фильтрации;

max

— максимальная мощность напорного или безнапорного пласта

(мощность грунтовых вод h

max

) в течение прогнозируемого периода;



min

— минимальный коэффициент водоотдачи (или недостаток насыщения)

напорного или безнапорного пласта. Если какие-то параметры из перечис-

ленных в течение прогнозируемого периода изменяются, то для расчета

max

по формуле ( 255) надо брать их экстремальные значения. Если этого

не предусмотреть, то на каком-то шаге времени может произойти наруше-

ние устойчивости и разрушение модели.

Таким образом, на модели надо отыскать такой узел, где параметры в

формуле ( 255) принимают минимаксные значения и по ним сделать расчет

max

. Нельзя для расчета брать средние значения, например среднюю

мощность грунтовых вод h

в качестве М

max

, так как это может привести к

 

min

max max

max min

; ,

k M

Dt a



 

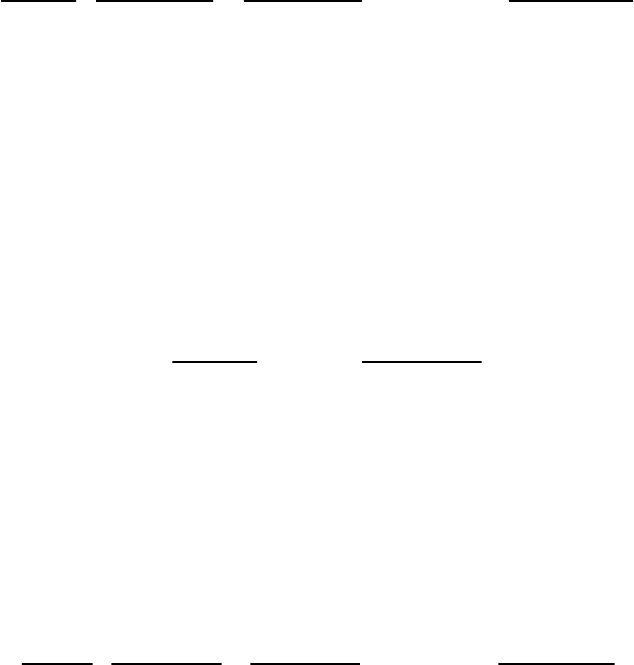
230

потере устойчивости счета модели. В таком случае надо принять М

max

равное максимальной мощности грунтовых вод h

max

, например

максимально возможную высоту купола грунтовых вод при выходе УГВ

на поверхность земли. О расчете Dt

max

см. [262] (пример 58).

Эти требования по применению критерия устойчивости ( 255) для

одномерных моделей относятся также и к двух-, трехмерным МКР-

моделям, использующим явные схемы формул моделирования.

Для двухмерных плановых МКР-моделей критерий устойчивости при

выборе шага времени для прямоугольной сетки по Н.Н. Калиткину [86,

с. 390]:

( 256)

где Dx

min

и Dy

min

— минимальные шаги соответственно по осям x и y из

принятых на модели; остальные обозначения см. в пояснении к формуле

( 255).

Для двухмерных плановых МКР-моделей критерий устойчивости при

выборе шага времени для квадратной сетки [284, с. 600]:

( 257)

где DL — пространственный шаг квадратной сетки; остальные обозначе-

ния см. в пояснении к формуле ( 255).

Для двухмерных профильных МКР-моделей критерий устойчивости

при выборе шага времени для прямоугольной сетки [86, с. 390]:

( 258)

а для квадратной сетки по ( 257).

Для двухмерных профильно-радиальных (осесимметричных) МКР-

моделей критерий устойчивости при выборе шага времени для

 

max max

max min

; ,

k M

Dt a



 

   

max max

2 2

max min

min min

1 1 1

; ,

k M

Dt a

Dx Dy





 

  

 

 

   

max max

2 2

max min

min min

1 1 1

; ,

k M

Dt a

Dx Dz





 

  

 

 