Смелов В.В. Лекции по теории переноса нейтронов

Подождите немного. Документ загружается.

O,llHH

nepBblK

HHTerpaJI

CHCTeMbI

(16.12)

yJKe

ObIJI noaysea nsnne

HCnOJIb30BaH

B, (16.10).

IITOObI

nOJIYllHTb

Jl-pyroH

nepBbIH

HHTerpaJI~

CJIOLKHM MeJKJl-Y

C060H

lIHCJIHTeJIH

3HaMeHaTeJIH

nepsux

,nByX

Jl-PO-

6eii

B (16.12),

YMHOJKliB

npenaapnrensao

lIHCJIHTeJIb

3HaMeHaTeJIh

nepaoa )(POO'H

It. B

pesyasrare

nOJIyllHM

d("~)=l[la,

T. e.

BTOpOH

HHTerpaJI

ecrs

a--->flJ.t

const.

(16.13)

nOCKOJIbKY

ypanneaae

(16.11) aeonnoponao, oomee pemenae

ero

cnezryer

sanacars

nepea nocpencrso nepasrx

HHTerpaJIOB

(16.8) H

(16.13)

CHCTeMbI

(16.12) B caenyromex

HeHBHOM

BHJl-e [24]:

(,VI

fLl,

a - 'fL)

===

0, (16.14)

rne

V-

npOH3BOJIbHaH

,nH<pepepeHII.HpyeMaH

epyHKUHH

Jl-BYX

nepe-

MeHHhIX.

113

oomero

peIIIeHHH

( 16.14) HY2KHO

H3BJIellb

reneps

TaKoe

lIaCT-

Hoe

penreaae,

tiTOObI

onpeneaaexaa

epyHKII.HH

a (If,

1J.t)

3aBHCeJIa

epYHKII.HOHaJIbHO

HaH,neHHOH

panee

epyHKUHH

.f}(r,J.t),

HJIH,

xro

2Ke,

JIeBOH

qaCTH

anrerpana

(16.8).

,aJISI

sroro

,nOCTaTOllHO

no-

rpeoosars,

qTOObI

HCKOMOM

qaCTHOM

peurenaa

BOBce

oTcyTcTBOBaJIa

JIeBaH

sacrs

narerpa.na (16.8).

CaMbIH

npocroa

pesynsrar,

BbITeKalO-

mHH

H3 oomero peureaaa (16.14),

KOTOpbIH

conepaorr

JIeBylO

xacrr,

mrrerpana

(16.13), HO

COJ(epLKHT

JIeBOH

qaCTH

narerpana

(16.8),.

HMeeT

BH,n a-f':J.t=O, T. e.

a(r,

"'1)

=~J..t.

B COOTBeTCTBJiH C

nepnux

paBeHCTBOM

'B (16.4)

HMeeM

X='fJ..t.

(16.15)

3aMeTHM,

liTO

nOCJIe

roro,

KaK

nOJIyqeHO

asrpaxceaae ,nJIH y

(16.10), asrpaaceaae J(JIH x (16.15) MOJKHO

JIerKO

yranars.

caMOM

,l(eJIe,

y===

rV1 -

fL2

rsin 6

(f!'===cos

6),

rorna

eCTeCTBeHHO

«3ano,n03pHTb»,

qTO

x=,r

cos

6=r

J.t

I1TaK,

ypaBHeHHH

(16.1)

npOH3BeJl-eM

aaxeay

nepeueaaux

tPopMyJIaM

X=fP.,

y===rV1 -

p.2

npe06pasyeM

ero

B~y

(r)

<p=+

(r)

<PI

(r)

(r)].

<PI

(r) = S

(r,

po)

dpo.

-1

120

(16.16)

(16.17)

(16.18)

06JIaCTblO

Onpe~eJIeHHH

<pyHKUHH

B HOBbIX

nepexeaaux,

KaK

3TO

cnenyer H3 <pOpMyJI (16.16),

6y~eT

nonyxpyr

+ y2<

y>O.

I'pa-

naua

pasneaa

.llBYX

cpen

r=R

H BHeIIIHHH

rpanaua

r=R.

nepeanyr

COOTBeTCTBeHHO B nOJIyoKpy2KHOCTU: X

+ y2= R2

(y>O)

H X

+ y2= R2

(y>O).

ECJIU

6bI

npanaa

lIaCTb

ypaBHeHHH

(16.17)

1 .

f(r)==2[Es(r)~o(r)+q(r)]

(16.19)

6bIJIa HaBeCTHa, TO

npa

JII060M

<pHKCHpOBaHHOM

3HaqeHHH

(0<

y<i.R

)

nrparotnea

POJIb

napauerpa,

MOiKHO 6bIJIO

6bI

JIerKO

onpenemrn,

peIIIeHHe

06bIKHOBeHHOrO AH<p<pepeHllHaJIbHOrO ypaBHeHH5I

nepsoro

nopanxa

JIHH""

(pHC. 23),

aerrpepsmaoe

B TOtIKaX L

H P

[CM.

(16.3)] H

nonnaaeanoe

yCJIOBHIO

(1\1)

==~

s'. y)

0, (16.20)

xoropoe asrrexaer aa

(16.2).

TOJIbKO liTO B@CKaaaHHOe

3aMellaHHe

nOaBOJIHeT C<pOpMyJIHpOBaTb

CJIe,nyIOIUHH HTepaUHOHHbIH

npouecc.

npOH3BOJIbHO

3a~aHHOMY

HallaJIbHOMY

pacnpezieneaaro

(ir)

aaxonax

<PYHKUHIO

<p,

pemaa

ypaa-

HeHHe

+E(r)ff=f

(r).

(16.21)

nOMOIUblO HaH,neIiHOH <pyHKUHH

<popMyJIe (16.18)

onpenenaex

cpo(r)

, a

sarea

<popMyJIe (16.19)

f(r).

,llaJIee

npouecc

nOBTopHeM.

o R

RIJ

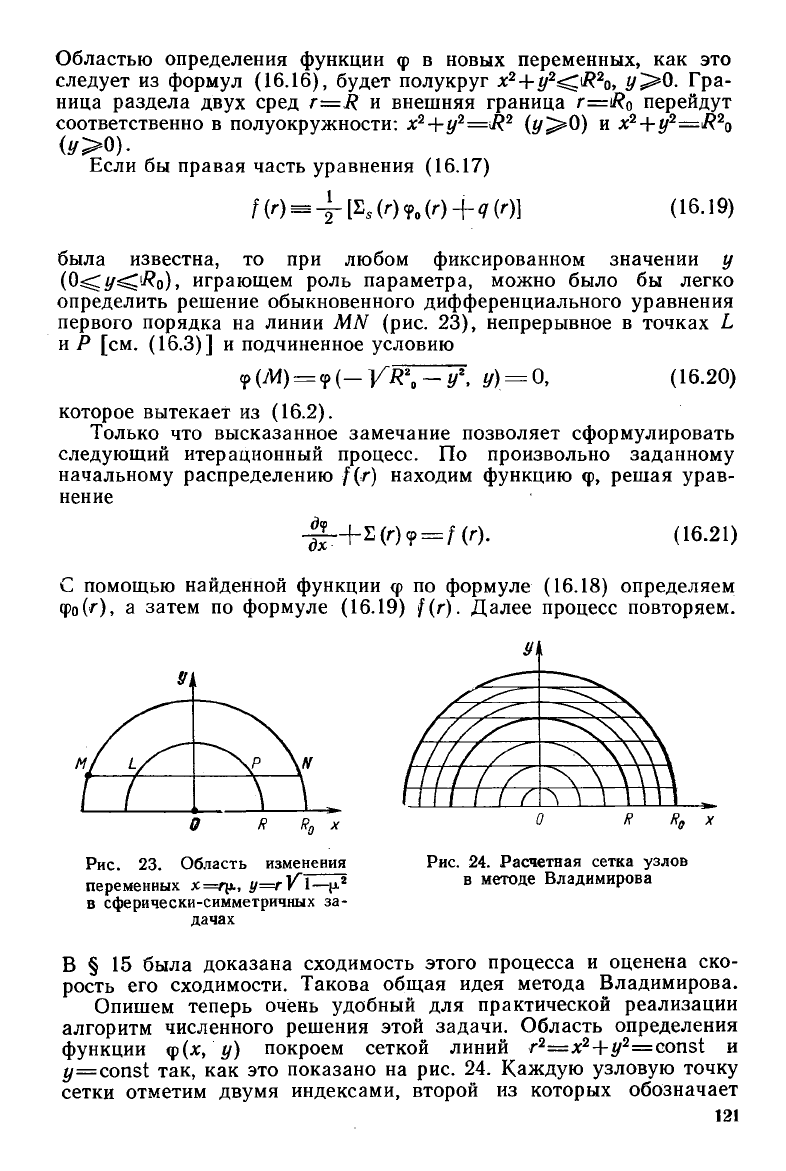
PRC.

23.

06JIaCTb

H3MeHeHHSI

nepesreaaax X=TIJo, y r Y

1_~2

c4>epHQeCKH-CHMMeTpHQHhlX

sa-

AaqaX

PHC.

24.

Pacseraaa

cerxa Y3J10B

MeTO~e

Bna~HMHpoBa

B § 15

6bIJia

AOKaaaHa

CXO.llHMOCTb

3Toro

npouecca

oueHeHa

CKO-

POCTb

ero

CXO,ll.HMOCTH.

Taxosa

otiutaa

H.lleH MeTO.lla

BJIa.llHMHpoBa.

OnHIIIeM

reneps

osens

y,ll.06HbIH

,lI.JISI

npaKTHtIeCKOH

peaJIH3aU

aJIrOpHTM tIHCJIeHHOrO

perneHHH 3TOH aa.llatIH.

06JIaCTb

onpe.lleJIeHHH

<pyHKU

<p(x,·

y) noxpoex ceTKOH JIHHHH

= x

+ y2= const

y=const

TaK,

KaK

3TO noxasaao

pRC. 24. Kazcnyro y3JIOBylO TOQKY

ceTKH OTMeTUM

.llByMH HH.lleKCaMIf, BTOpOH 1I3 KOTOpbIX

060aHaQaeT

121

HQMep

KOOp,lI.HHaTHOH

,JIMHH"

y=const~

HaqHHaH

JIHHHB'

y=O.,

nepBbIH

nOpH,l{KOBbIH

HOMep

TOl.JKH

KaJK,l{OH H3 JIHHHM

y=const

CJIeBa

aanpaso,

Hal.JHHaSl C

TOllKH

(CM.

pHC.

23).

TaKHM

o6pa30M,

eCJIH

,k-

nOp5l,l{KOBhIH

HOMep

OKPY}KHOCTH,

Hal.JHH·aSl C

BHeWHeA,

TOqKH

nepecesenaa

JIHHHeH

Yi 6Y.lJ.YT onpeneasrrscs

«HH,neKcaMH»

(k, i) H (k

i),

rne

k'=ttV-2(i-l)-(k-l)

-l.JHCJIO

Y3JIOBbIX

TOl.JeK

JlH·HHH

y=O).

HT8K,

nycrs

KaKO'M-TO

HTepaIJ.oBOH~HOM

ware

npaaas

qaCTb

ypaBHeHHH

(16.21)

H3BeCTHa

ncex

Y3JIaX

ceTKH.

"MbI

oy,neM

onacuaari,

XOpOIIIO

H3BeCTHbIe

.KOHetIHO-pa3HOCT-

asre

xeronx

peurenas

sanasn

KOIliH

,nJIH

JIHHeHHOro

OObIKHOBeHHoro

,llH<p<pepeHIl;HaJIbHOrO

ypaBHeHHH

nepsoro nopsznca.

tIHTareJIb,

3HaKO-

MbIH

KpaHHeH

Mepe

C O,lI.HHM H3

TaKHX

MeTo,noB,

JIerKO

nOJIyqHT

,nHcKpeTHoe

peurenae

aanaun

(16.20), (16.21)

Ka)f{,lloA

JIH-

HMB

tn:

(()l

<P2i,

•.••

, q>ki,

•••

(16.22)

nOCJIe

Toro

KaK

onpeneaenu

3HalIeHHH

<Phi BO

scex

Y3JIaX

ceTKH,

aerpynno

nOJIYllHTh

npH6JIH)I{eHHOe'

anaxeane

Q>yHKUMH

cpo(r)

[CM.

(

16.18)]~

BOCnOJIh30BaBWMCb

xaanparypaon <l>OpMyJIOH

CPo

(rk)==

~aki

(CPki

CPk1i)'

rne

CYMMHpOBaHHe

npoBo,nHTCSI

ncex

TOlIK8M

nOJIyoKpyJKHOCTH

HOMepoM

aki

K03<pqn'IUHeHTbI

xaanparypnof

<l>OpMyJIhI

,lI.JISI

TO-

qeK

,naRHoA

OKpy:>KHOCTH.

Haxoneu,

<j>opMyJIe

- (16.19) naxonax

HOBbIe

3HaqeHHH

f(rk) ,nJISI

cnenyiomero

HTepaUHOHHoro

mara

H T. n.

3 a M

a H H e 1. Tlpa pemeaaa

ypaBHeHHSI

nepeaoca

'MeTO,llOM

BJIa,llHMHpOB3~

T810Ke

Sn-MeTO.llOM,

0 KOTOPOM 'l10H.lleT

tpellb

B cneayiomea naparpaipe, ,HCnOJlb3yeM

HTepaUHOBHhlH

nponecc.

qaCTo

TaKOH

rrponecc MO>KeT OK338TbCSI Me.!lJleHHO CXO,lUI-

III,.HMCSI.

,B '3TOM caysae Ue.n.ecOO6p33HO

npHMeHSITb

MeTO,llbl yJIy1fWeHHSI

CXOJJ.HMOCTH

nocaenoaareasaax

npH6JIH>KeHHH.

O,ZlHH H3

TaKora

pona MeTO,ll.OB

paCCMOTpeH

B § 18.

ooJlee

'UoJtpoOHhle

C·BeJl.eHHSI

3TOMy

aonpocy

1IHTaTeJIb

MO:>KeT 'HaRTH,

H8IIpH'Mecp,

MOHorpa'CjlHSlx

[3, 15]. .

3 a M e 11a H 'II e 2.

HeJlJWlHe

'HMeTb

B aany, xro

nepexon

OT TOll"HOH

38Jla1lH

(16.17), (16.18) ·K

KOHellHo-pa3HoCTHoH

.MO,ll.eJIH

JIHWaeT

Hac

npasa

ne30rOBOpOtlHO

CCbIJIaTbCSI

pesyasrara

§ 15- oOOCHOBa'H'He

HTepanHOHHOH

npouenypss

OIleHKa

. CKOpOCTH CXO,llHMOCTH HB OCHOBe § 15 HOCHT B 3TOH

cHTyanHHHecTporHH

xapaKTep.

«CTpOrOCTb»

MOJKHO BOCCTaHOBHTb, eCJIH B

pe3YJlhTare

npHMeHeBBSI

nponeaypu § il5

oneparopax

pa3HocTHOH

MO,lleJIH

noaysars

ouenxy

THna

(15':

16).

t7.

Sn-METOA IMETOA KAPnCOHAJ

OCHOBHhIe

nnea

aaaaraexoro

MeTo,na

ObIJIH

snepaue

C<}lOpMyJIHpO-

BaHhI

KapJICOHOM

'[29, 30]. Iloannee

Sn-MeTon.

nenpepuaao

pa3BH-'

BaJJeH

'coBepmeHCTBOB8JICH

H K

HaCTOHDleMY

BpeMeHH

C<j>OpMHpO-

BaJlCH

nepcnexrasnsnl

IIIHpOKO

npHMeHSleMbIH

3JIrOpHTM.

Czenyer

OTMeTHTb,

xro

nOMHMO

I\apJICOHa

HerO

aapyeescaax

KOJIJIer

oxens

KpynHMA

BKJIaA

pa3BHTHe

MeTon.a

BHeCJIH

COBeTCKHe

CneUHaJIHCTH.

lIaCTHOCTH,

HaCTOHmeM

naparparpe

aaman

OTp8JKeHHe

peSYJIbTa-

T:&I

noayseaasre B. H.

MOPO'30'BhIM

[31]. .

122

MhI

npOHJIJIIOCTpupyeM

MeTO,n

'Ra

npaaepe

ypasaenaa (16.1)'.

KO-

Topoe ObIJlO paccaorpeao B § 16 ,l(JIH

c<pepHlIecKH-CHMMeTpHtlHbIX

OOJIaCTeH

C H30TponHoA·

tPyHKUHeH

paccesnas

H30T.ponHhIMH

HCTOq'..

HHKaMH.

,llH€p<!>epeHUHaJIbHYIO

sacn,

sroro

ypaBHeHHSI

HaM

y,l(06HO

ceAqac

sanacars

B COOTBeTCTBHH C

npe,l(CTaBJIeHHeM

(10.28). KaK

H B § 16, npenrronaraeu

HcnOJJb30BaHHe

arepauaoaaoro

npouecca,

QTO

n03BOJIHeT

paccaarpaeart,

ypaaaenae

(16.1) B

BH,l(e

(17.1)

rne

npasyio

sacrs

,{(iT)

KaiKJlOH

J:fTepaUHH

CqHTaeM

H3BeCTHOH

paBHOH

(r)=-2-

[Esfo(r) +q (r)],

<P.

(r)

- S

(r,

po)

dpo.

-1

(17.2)

BHeIIIHeH

rpaaaue

rpanauax

paanena

cpen

HCnOJIb3yeM

yCJIO-

DRSI (i6.2) H (16.3).

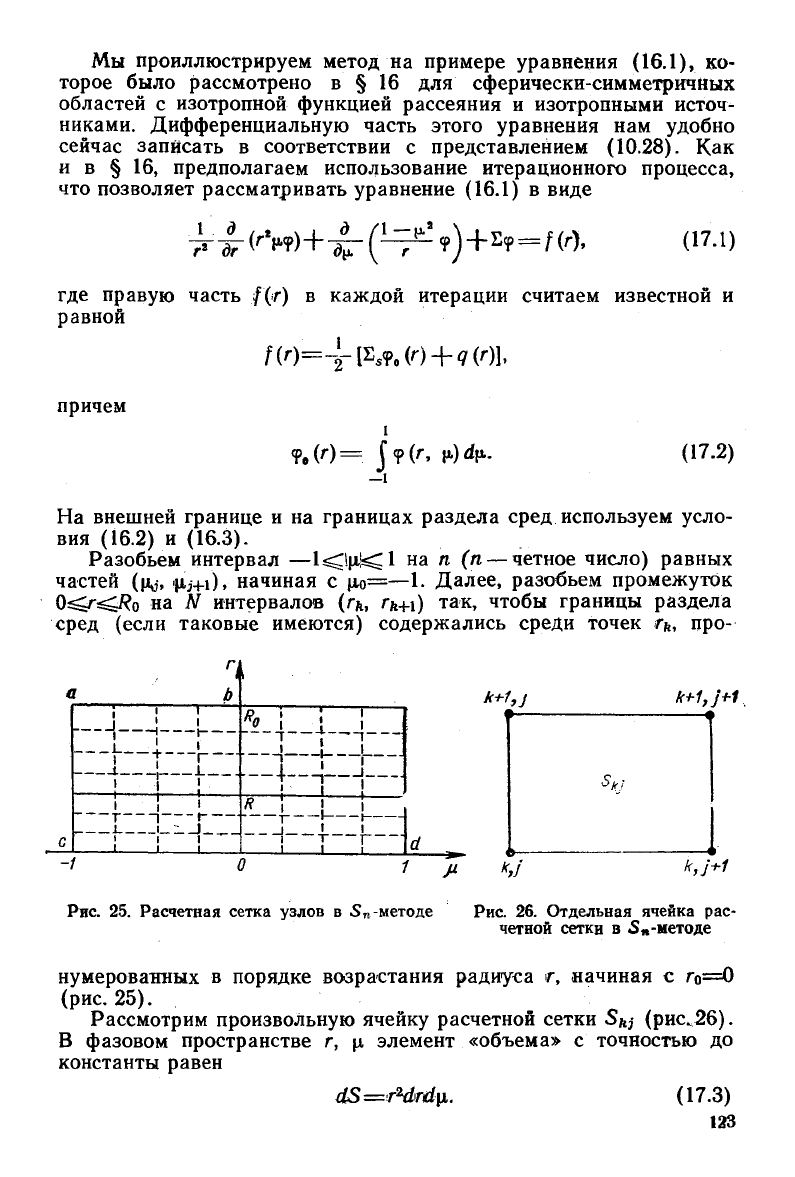
Pa300heM

HHTepBaJi

-1<\J1!~1

(n-qeTHOe

tIHCJIO)

paBHbIX

xacrea

(J\j, 'Ili+l), HaqHHaH C

f.1o=-I.

,UaJiee, pasorisea npoxeacyrox

O~~o

IfHT~pBaJlO'B

(fA, rA+l)

TalK,

lITOOhl

rpaaansr

pasnena

'cpe,n

(eCJIH

TaKOBble

HMeIOTCH)

conepxcanacs

cpena

TOqeK

ifk,npo--

k+1,j+I.,

k+1,J

I I

......

-------

...

.J I I 0

I--~---r--

--i--~--'---

---t---'t--+--

---l---~--:---

--~

~--L--

~--,--~_--

,I I I - I

-1 0 1

k,j

PRC.

25.

PaCqeTHaH

cerxa

Y3JlOB B Sn -xerone

Puc. 26.

OTJ1eJIbHaB

HqeHKa

pac-

qeTHOH CeTKH B Sfa -aeroae

HYMepo-aa'HHblX

a nopaaxe

sospacraaaa

pannyca

If,

H~qHHaSl

To==O

(pHC. 25). . . . ,

Paccxorpax

npOH3BOJIbHYlO

HtIeHKy

paCtIeTHOH

CeTKH

Ski

(pHc",26).

epa30BOM

npocrpaacrse

3JIeMeHT

«OO1>eMa»

C TOqHOCTbIO no

KOHCTaHTbI

pasea

(17.3)

123

(17.4)

Ilponarerpapyea

yp3BHeHHe

(17.1) B npenenax

HqeHKH

Sus e

yseroa

(17.3):

'k+l

=.61'

(r)

dr,

rne

L\fJ.=

fJ.j+l-fJ.j.

npe06p330B3HHe

nepnux

,ZlBYX

CJI3r3eMbIX

npe,lI.CT3BJIHeT

Tpy,lI.3,

TaK

qTO

pe3YJIbT3Te

HMeeM

SJ.j+l

....

j+1

rZk+1

p.rp

k+J'

1')dp. -

r',

p.rp

k. 1')dp.+

....j ....j

'k+l

p.Z/+I)

rrp

(r,

p./+J)

p.Z/)

rrp

(r,

1'/)

'k+l

SJ.j+1

'k+l

+ J

r,(r)rZdr

(r,

p.)dp.=.6p.

f(r)rZdr.

....

npenenax

SlqeHKH

Ski

armpoxcaanpyea

<PYHKIlHIO

(r, ;fJ.)

HHTep-

nOJIHIlHOHHOH

<pOpMyJIOH,

K'OTopaH

nOJIyqaeTCH

pe3YJIbTaTe

nocneno-

B3TeJIbHOro

ocyme'CTBJIeHH5I

JIHHeHHOH

HHTepnOJIHUHH

CH3qaJIa

O,llHOH

nepexenaoa,

33TeM

,llpyroH

(pe3YJIbT3T

33BHCHT

nopH,ZI.Ka

npOBe,ZI.eHHH

nOCJIe,nOB3TeJIbH@X

HHTepnOJI5IIlHH):

1 "

f (r,

p,)=

~rk~tJ-

[(r

- r) (Jl-j+t

p.)

epkj

(rk+l

(p.

P-j)

epk,

j+l

+(r

'k)

(P.j+l -

P)CPk+l,

+(r-r

(p.-l-Lj)CPk+l,j+l]'

(17.S)

rne

<pkj-3HaqeHHe

<pyHKUHH

<p(lr,

:J1)

TOqKe

(rlt,

J.1j);

~'Tk=

Tk+l-Tk

IIIar

nepexeaaoa

KOTOp@H

MO}KeT

6bITb

nOCTO:-

HHHbIM,

BCJIe,ZI.CTBHe

nero

MbI

HCnOJIb3yeM

HH,ZI.eKck.

COOTBeTCTBeHHO

<PYHKUHIO

f(Ir) B npoxexcyrxe

'It~

r.~ifk+l

annpOKcHMHpyeM

JIHHeHHOH

HHTepnOJIHUHOHHOH

<l>O~MYJIOH

1 .

(r)

==~

[(rk+l

fk+

- Tk)f

k+l].

(17.6)

~rk

nO,nCTaBJIHH

(17.5) H (17.6) B (17.4) H

BblnOJIHHH

nee

HHTerpHpoB3-

HHSI,

nOJIyqaeM

Ak/fkj

+Bklfk+J,

Ck/Pk, J+l +D

k+l ,

j+l

==Ekf

Fkf

k+l'

(17.7)

124

r,ne

Akj=-rlkp.;Ap.-(l-p.lj)rtArk+

1::

(r1k)+ArkAp.;

Bkj=rlk+tp.;AP.-(I-p.lj)r;;+lArk

1)-Ar

kAp.;

= -

rlkp.~lAP.+

_p.l

)

rtArk+

(r1k)+ArkAp.; J(17.8) .

rlk+tp.~+lap.+·(1

p.2

)

r-;+ta'k +

(

k+l)-

ArkAp.;

Ek=(r2k)+arkL\p.;

= (

k+t)-

ark~p.,

2fJoj

+fJtj+l

P-

= 3

r+= 2rk + Tk+l

k 3

2P.j+l

fJoj

•

P.j+l=

3 '

- _ 2rk+ 1 +Tk •

'k+t-

t·

(17.9)

06paTHMCSI

reneps

onncaamo

QHCJIeHHOH npouenypu,

n03BOJISlIO-

meA

HeKoTopOM

rrOp~,llKe

rrOCne,llOBaTeJIbHO

orrpe,lleJIHTb

3HaqeHHH

CPkj

OCHOBe

pasencraa

(17.7).

I'panasnoe

yCJIOBHe

(16.2)

oaaanaer

paaeacrno

HyJIIO

3HaqeHHH

<pyHKUHH

Y3JIa~

JIHHHH

abo

(CM.

pHC.

25),

T. e.

CPNj=O

(j=O,

...

n/2).

OTMeqeHHOe

06CTOHTeJIb-

CTBO

noncxaaanaer:

rrOCJIe,llOBaTeJIbHOe

BblqHCJIeHHe

3HaqeHHH

Y3JI3X

ceTKH

HyLKHO

BblrrOJIHHTb

<popMyJIe

(17.7),

HaqHHaH

3HaqeHHH

JIHHHH

ab H

nponsaraacs

BHH3

JIHHHH

(CM.

pHc.25).

Jlerxo

y6e,nHTbcH,

O,llHaKO,

qTO

QHCJIO

HCKOMbIX

BeJIHqHH

<Pkj npeasr-

tnaer

qHCJIO

ypaBHeHHH

(17.7),

noroxy

sanasa

OK33bIB3eTCH

aezio-

onpeneaeaaoa.

Onaaxo

cncrexy

ypaBHeHHH

(17.7)

JIePKO

noonpene-

JIHTb

HeKHM

KOHeqHO-pa3HocTHbIM

COOTHomeHHeM,

CBH3bIBalOIII.HM

HC-

KOMbfe

BeJIHqHHbI

q>kO

JIHHHH

(CM.

pnc,

25).

caMOM

nene,

eCJIH

ypaBHeHHH

(17.1)

nOJIOLKHTblJ.=-I,

TO OHO

otipautaerca

06bIK-

HOBeHHoe

,llH<p<pepeHUHaJIbHOe

ypaBHeHHe

rrepBoro

nOpH,llKa

nepe~

MeHHOH

0,+

-dr

Ecp(r,

-I)=/(r)

Haq3JIbHbIM

yCJIOBHeM

(i7.10)

cp(R

-1)=0.

(17.11)

ECJIH

renepr,

sanauy

Koum

(17.10),

(17.11)

pemars

KaKHM-HH6y,nb

KOHeQHO-pa3HocTHbIM

MeTO,llOM,

MbI

npanex

KOHeQHO-pa3HOCTHOH

125

tj>opMyJIe

OTHOCHTeJIbHO •

BeJIHtIHH

q>kO,

npHQeM

(J'NO=O*.

npe,llDOJI01KllM,

lITO.

3TOAOnOJIHHTeJIbHOe

ypasaeaae

peureao, T. e.

H3BeCTHhI

saaxe-

HHR

(j>

Y3JIaX

JIHHHH

(CM.

pHC.

25).

3HatIeHHSI

<PA;

yaJIOBIiX

TOtIKaX

(k,

np~

l~i~n/2

MorYT

6biTb

onpeneaeau

epopMyJIe

epkj=G;fk+l.

i +

R~,

(17.12)

r.a.e

a;;;

==- D

•

-lICk,

i-I;

Caenyer

ocoticrronsepxnyrs,

sro

CtIeT

ecaepxy -

BHH3»

$opMyJIe

(17.12)

npa

1~j~n/2

cosnanaer

HanpaBJIeHHeM

yCTOHtIHBOCTH

CQeT8.

Ilpa

nt2<j~n

cser,

aanporas,

YCTOHqHB

«cH'Hay:..-

saepx».

3TOM

cnysae

pacxeraaa

$opMyJIa,

noaynaexas

H3 (17

7),

H~eeT

BH,l{

(17.13)

r,11e

= - C

•

i-I;

Rt=

Dk.1f_1

(Ekfk+Fkfk+J

Ak.i-llPk.i-1

-8"k.l-llk+a.I-

) .

,[lJIR

peaJIH3aUHH

cxera

<popMyJle

(17.13) HY>KHO

3HaTh

saane-

HHB

epyHKUHH

JIIHHHHOd

('OM.

pac, 25).,

HaH60Jlee

eCTeCTBeHHO

-3TH

3Haq~HHSI

nOJIytIHTb

CJIe,nYIOIUero

YCJlOBHSI, otiecnenaaajomero

HeHTpOHHhIH

OaJIaHC

B ueurpe

c<j}epbI:

q>Oj=<Po,

n-j,j>n/2

nOCJIe

roro

KaK

3HaQeHHSI

<pyHKUHH

q>kj

nOJIyqeHhI

scex

Y3J1ax

paCtIeTHOH

ceTKH,

nerxo

no,nCQHT3Tb

,nJlSlCJIe,llYIOIUeii

HTepaIlHH

SHa-

qeHHSI

<pyHKUHH

<po

(Ir) (17.2). B COOTBeTCTBHH c

annpoxcauanaea

(17.5)

HMeeM

lP.

(rl)

= A;

~lPk'

+2lPkl

2lPki

+ .••+

2rpk.

"-I+lPkn)·

Zlaaee

HTepaUHOHHhIH

npouecc

MO)KeT

ObITb

nosropea

aeotixonaxoe

QHCJIO

pas

(B03MO>KHO,

npHMeHeHHeM

yCKopeHHSI

CXOJ(HMOCTH).

06ocHoBaHHe

(aecrporoel) CXO,llHMOCTH

HTepaUHOHHoro

nponecca

Sn-MeTo,na

CJIe,nyeT·H3

'§ 15

(CM.

TaK2Ke

3aMetIaHHe

2 K ,§ 16).

3 a Me.q a H

He-

BWlIe6hIJI

yxasaa TOT

lIOPSIJI:OK

'IlOCne,Zl.OOaTeJIbHOrO

BbIlIH~Jle

HHH 3

eHiHH

«P1&l,

KOTOPblH Heo6xo.ll.HM )J.JUI

YCTOHQ'HBOCTB

S,,-aJIrOpHTMa

[12].

·B

JJ.yxe

asaaraeaoro

MeTOAa

!KOHetIHo-'pasHocTHYIO

a1I1IpOKCBMaUHIO

ypasne-

HHH (17.10) ecrecraeaaee acero

peaaasoaars

'B upeA1JIOJlO1KeKBB

JIH:HeHHOCTiH

4JYHK-

~HH

<p(r,

-1)

Me1KAY

'Ka1K,ZI.OH

napoa pacseraux YSJIOB aa

JI'B1I'HH

ac '(!CM.p'HC. 25).

126

O.!t-H8KO

npeJlJlaraeMhlH

nOpH.D.OK Bbl'IIOJlHeHHH BhIqHCJleHHH

-~BJISIeTCH

.Il0CT3TOllHhIJE

YCJlOBHell

ycroiiqlmOCT.H.

ReKOTOpOM

CMhlCJle

POJIb

.ztOCTaTOllHoro

YCJIOBHB

-lIDpaeT

Tpe6oB8HHe

nOJIO>K'HTeJIbHOCTH K03$«I>HUHeHToB

Gkj

H·

ai!i

Stj)opMyJlax

f17.12) B

(17.13) (12). 3anHUleM

ynoMSIHYThie

Ko~clJHU'HeHThi

B q>op-Me ·paSJlO>KeHHB no

nap8--

MeTpy

8k=4I-",/r/&:

rae

akj

= (2

Ip.

/ I- Ek

/(2

IIJ'

11+Ek

4rk).

llJUI

nOIJ.3

&TISlIO~erO

60JIbmH~eTBa

TO-

qeK

ceTKH

ecr

s M3JIh1H napasserp, 3

nOToMY

SHaK

G:J

npeHMYnt.eCTBeHHO

onpene-

JISleTCB

3BaKOM

akj.

CJle.n.OB3TeJlbHO,

Tpe60Ba

HHe ali>0 CBOJI.HTCB B

arore

He-

p3seHcTBy

3 3

e q a H

e 2.

KaK

caenyer H3 y-p3BHeBHSI .( 17.1)

-T3K1Ke H3

co06pa>KeHHH

CHMMeTPH~H,

B IleHTpe

-H3yqaeMoH

ctj)eplll lJIOTOK He.

.llOJDKeH

aaancers OT -

yrJIO'BOH

.KO-

opllHHaThI,

T. e. BO

scex

TOtIKaX

JIH'RHH

'(eM.

'PHC. '25)

SHalleRHH

epyHKUHH

,l1.0JDK-

HhI

6hITb

pa'BHhI

,llpyr .u.pyry:

<J'OO=tq>Ol=(f>OF=

•••

=q>o.n-l=q>On.

3To

06cTOBTeJlb-

CTBO B

paCqeTHOM

aMopHTMe He

OTpa>KeHO,

a 'lIOTOMy

'IlpHBe.aeHU8S1

uenoxxa

paaeacra

MO)f(eT CJIY>KHTb KOBTPOJlbHhIM K-pHTepHeM TOlJHOCT1i· pacsera.

§ 18. &AnAHCHWM

METOA

YCKOPEHHSI CXOAMMOCTM

MTEPAL\MOHHOrO

nPO~ECCA

cnynae

Me,l(JleHHOH

CXO,l(HMOCTH

MeTO,na

BJIa,l(HMHpOBa,

Sn-Me--

rona

HJIH

JII06oro

npyroro,

OCHOBaHHoro

HTepaUHOHHOM

npanuane

(

15.1

)

npHxo,nHTCSI

npaoerari, K

npaexaa

YCK.OpeHHH CXO,nHMOC-TH.

Onmnex

O,nHH H3

TaKHX

npHeMOB,

KOTOphIH

MO}KHO

Ha3BaTb

6aAaHC;..

HbtM

MeToiJoM

YCK,OpeflUfI,

CXOOUMOCTU.

3TOT

MeTO,n

H3BeCTeH

yJKe

cpaBHHTeJIbHO

,naBHO

[~2]

C ycnexox

npHMeHHeTCSI

KaK

npa

peme-

HMH O,nHOCKOpOCTHhIX sanas,

TaK

H B

np06J1eMaX

MHorOCKopOCTHOii-

reopaa

(ca. § 30). Hs

MHorHX

npHeMOB

yCKopeHHH

CXO,nHMOCTH

OCTa-

HOBHMCSI na

6aJIaHCHOM

BBH,ny

ero

npocroru

rJIy6oKoro

<pH3HQeCKo-,

conepacaaas.

MTaK,

paccaorpax

cxO,nHIUHHC~

HTepau.HoHHbIH

npouecc

(15.1),.

KOTOphIH

KOpOTKO

MOJKeT

6bITh

sanacaa

<}lopMe

(18.1

Oneparopsr A, B H $Y'HKUHSI Q onpeneneasr na

c.-

li13.

·npe,llnOJIOLKHM,

qTO

··B

ypaaaenae

(15.5)

no,nCTaBJIeHO

pemeaae,

peayasrare

qero

nOJIyqeHO

TO)K,neCTBO~

YMHOLKHM

3TO

TO}K,neCTB()

CKaJIHpHO

'[eM.

(15.3)

]Ha

aexoropyro <PYHKII.HIO p

(r,

>0:

([A-B]<p,

p) = (Q,

p).

(18.2}

• H3 CCYUlOK

1Ia

OTJleJIbHble

'l»opMyJIhi

§ 15 He

cnenyer,

xro

npensapareasaoe

HsyqeHHe

'§ 15

o6BS8TeJlbHo.

127'

ECJIH

~TepaUHOHHbIH

nponecc (18.1)

npa

,naHHOM

erne

H~JIh3H

ot)o-

paart,

(paanocrs

cp(n)--Icp(n-l)

3aMeTHO

OTJIHqaeTCH

HyJISI)

, TO

paCCMaTpHBaeMOM

HTepaUHOHHOM

arane

<pyHKUHH

(()(n), nootime

rOBOpSI,

y,nOBJIeTBOpSIeT

paseacrsy

(18.2),

TaK

KaK

OHa

3TOM

CJIyIIae

nO,ll.IIHHSIeTC5I

,npyroMy

COOTHOllIeHHIO:

([A-B]ep(n>, p)===(Q,

p)+(B[cp(n-l)_ep(n)],

p).

113

nOCJIe,nHeH <}>OpMyJIhI BH,nHO,

lITO

rpedyexoe

paseacrao

(18.2)

3a-

Be,ll.OMO

y,noBJIeTBOpSIeTcH

TOJIbKO

npH

n-+oo.

A eCJIH

MO,nHq>HUHpoBaTb

HTepaUHoHHhIH

npouecc (18.1)

TaKHM

o6pa30M,

IIT06bI

Ka)K,nOM

HTepaUHoHHoM

nrare

BbII10JIHHJIOCb

pa-

BeHCTBO (18.2)?

XOIIeTC5I

,nyMaTb,

lITO

3TOT

npaesr

enoncrer-aer»

HTe-

paUHOHHbIH

npouecc

yCKOpHT

ero

CXO,nHMOCTb.

nOCJIe

Toro

KaK

BbICKa3aHa

06ruaSI

H,ll.eH, MO,nH<pHKaUHIO.

HTepaUH-

ormoro

npouecca

yxce

JIerKO

npnnyxars.

MOJKHO,

aanpaxep,

nOJIy-

IIeHHyIO

<PYHKUHIO

!(j)(n)(r,

YMHO)KHTb

aexoropyro

KOHCTaHTY

C«,

nO,ll.06pa

IHHYIO

T.aKHM

pacaerox,

qTo6bI

<py'HKUHH

Cnq>(n)(r,

y,ll.OBJIeTBOpSIJIa TOLK,neCTBy (18.2). B

arore

npHXO,ll.HM

cnenyiotneay

MOJJ:H<pHUHpoBaHHoMy

npoueccy:

(18.3)

rne

~(n)

CJIeJI.yeT

paccxarpaaars,

KaK

aexoropsra npOMeJKyTOqHhIii

pesynsr

ar,

(18.4)

(18.5)

nOJIYIIeHHoH

tpopxyne

(Q,

p)=F.O,

TaK

KaK

p>O, a <PYHKIlHH

HCTOq-

HHKOB

ueorpnuarensna

panna

TOLK,neCTBeHHO

HyJIIO.

CJIe,nOBa-

TeJIbHO,

Cn=FO.

XOTSI

,nOKa3aTeJIbCTBO

CXO,nHMOCTH

npe,nJIOJKeHHOrO

MO,nH<pHIlHPO-

BaHHOrO

npouecca

06meM

cnyxae

nOJIyqeHO

[;15],

npaxranecxoe

npnxeaenne

aJIrOpHTMa

(18.3) B

pane

cnyxaea

secsaa 3<p<peKTHBHo.

3 a M e q a H H e

MSI

BblQHCoI1eHHSI

K03<fl<flHUlieHTa

HCnOJlb3yeTcSI,

npelKAe,

acero,

Y}I{e

HaiiAeHHaSl

4lYHKIlHSI

A~(n),

pasaas

B,(n-l)

[CM.

(18.3)].

BhlQHCJle-

HBe

BTOPOH

~YH~HH

~(n)

«He

nponaAaeT

AapOM»"

TaK

KaK

BenHqHHa

B,(n)

Heoo-

XO,!{BMaSl AJISI BhlnOJIHeHHH

CJIeAYIOm.ero

HTepaUHOHHoro

mara,

onpeneaaerca

epop-

qMyJTe

B<p<n)

CnB'<n).

ella

H H e 2.

HcnoJ1b3YSl

nepsoe U3

paeeacrs

(18.3), HeTpYJJ.Ho

nOJIy-

8Th

AJISI

CJIeAYIOmyK> epOPMY

JlY:

(B (;<n) _

ep(n-l)],

= 1 +

---..;...,

--.;.----~---.;---

(Q, p) - (B

(f{n)

- <p<n-l)] , p)

OueHHM

B 3TOM Bblpa>KeHHH CKaJISlpHOe

npoasseaeaae

(B [f(n) - <p(n

-1)]

p).

nOJIa-

ras,

liTO

ecrr, TOqHOe peuieaae 3a,u.allH (15.5), 0OO3HaQHM

~<n)

-fen); e(n) =

,en).

BbIqHTaSl

nepsoe

paseacrao

(18.3) H3 (15.5),

nonysaea

A7<n)

=B€(n-l)

HJlH

7(n)

-lB€(n-l).

128

c·

yqeTOl\1

oiJ.eHKH

(15.16)

HMe6i·

OTCIO,lla

1I,<n)

- ,<n-I)II = IIs<n-l)-

;(11)11

lle(n-l)1l

+1I;(n)1I

ns(n-l)lI.

Haxoaeu, c ,HCnOJIb30BaHHeM

lIepaBeHcTBKoWH

BY'HSfKoBCKoro

IJI

IIBII~I

i(CM. § 15)

HaXO.llHM

ouenxy

CKaJISIpHOrO npOH3Be.ll.eHHH

I(B(fin) -

,en-I)],

p) I

liB(;in) - ,<n·-I»II·lIp(l<

Bll·llpll·lf'<n)

,<n-l)1I

IIpU·ll

(n- l}

1/.

B cnysae CXO,ZJ.SlmerocSI

arepanaoaaoro

nponecca (18.3) Jl8(n)II--+0

'D-pH

n--+oo~

BcooTBeTcTBHH

lJIOJIyqeHHoH'

uenOtIKOH

HepaBeHCTB

3TO osaaxaer,

liTO

CKaJISlpHOe

.npOIf3'BeJJ.eHHe

(IB[q;(n)~cp(n-1)],

p)---+o.

nOCKOJIblKY

(Q, .p)

=#=0,

TO ;H3

q»OpMyJlhl

(18.5) CJIeJly.eT, nro

Cn--+I

'IIpH

.'n~oo~

,nOCneJliHHH

pe3YJIbTa1'

n03BOJISleTB

H3BecT·

HOH

CTeneHH·

CJIe,Z(HTb sa

'HTepaIlHOHH~M

'nPOIlecCOM~

JII06.0M

cnyxae

ero

cnenyer

06pbfBaTb,

noxa Cn

«3aMeTHO

OTJIHlIaeTCSI 01'

eAHHUUbl».

Haxonen, iJIOJIe3HO

06paT,HTb

'BHHMaHHe

erne na O,Z(Hy neraas, A

UMeHHO:

'lIO

Mepe

upH6JIHiKeHHSI

napaxerpa

Cn K enanane Bee cnaeee -ecpatiarsraaer»

aropoe

ypasae-:

'HHe (18.3).

3TO

osaaxaer,

liTO

C'pOCTOM

n MO.lI.H<pHllHPOB8HHhiH nponecc UOCTeneHHO

cr3HOBHTCSI

nosra

3KBHBaJIeHTHhlM

arepanaoanoay

anroparay

,(18.1).'

,llPYfHMJI

CJIO·-

Ba'MH,

MO,Il.H<pHIlHlpoBaHHbIH nponecc

(t8~3)

HaH6oJIee3qx}leKTHBea

nepssex arepa-

UHSlX,

lITO

n03BOJISIeT-

6hICTpO

'IIOJIyqUTb

:«13

06mHX

'lIepTax»

Heil'rpOHHOe

-ooJle.

no-

CJIe.LI.YlOlIJ:HX

HTepaUHSlX

(npa C

n~l)

HallHHaeTCSI

y:>Ke

60JIee

Me,ZlJIeUH3S1

«mJr~OBKa»

sroro

nOJISI. ·KCTaT,H,

TaKOH

xapaxrep CXO.llHMOCTH

npHCYIIl

·K !JIeKOTOlpbIM

p-pyrBMHTe-

pauaonaua

.MeTOj{aM,

aanpaaep

MeTO.llY

MJlHHMaJIbHhlX

;HeBSl30'K [33, 22J.

aCCMoTpHM

Tenepb

BaLKHbIM

qaCTHbIH·

"CJIyqaH,Kor.na

·1.

BbI-

nHllIeM

Heo6xo,l(HMbIMH

;~pe06pa30)3aHHHMH

lKaJK,l(bIH H3

3JIeMeHTOB

paBeHCTBa

(18.2): .

(Aep,p)

ldVJ

dQ(Q\7ep+~ep)=

~dV

SepdQ+ J

dQf

'\](Oep)dV.

v V

Ilpeotipasya nropoe

cnaraexoe

$opMyJIe I'aycca-i-Ocrporpancsoro,

nOJIyqaeM

(Aep,

p) =

~dV

SepdQ

+SdQ

QnepdS.

v "--8

yserou

rpaaaxuoro

yCJIOBHH

({)(rs,

==0

npa

gn~O

HaXO,l{HM

OKOHtIaTeJIbHO

(Aep,

p) = SE

(r)dV

(r,

O)dQ+

dS S Qnep(r, a) dQ.

v . s

00::::;0

BTOpOH

3'JIeMeHT

paseacraa

(18.2)

npHHHMaeT

COOTBeTCTBeHHO BH,n

(Sep,

p).=

IdV S

~s<r)dQ

Sg (r,

00')

(r,

a')

dQ' . .

v ~

(r) dV S

ep.(r,

a')

dQ' Sg (r,

00')

dO,

9-301