Ситник В.Ф. Системи підтримки прийняття рішень

Подождите немного. Документ загружается.

розглядатися як реальна стартова точка в даній галузі знань

1943 року ці автори опублікували свої результати в книзі

«Логічне числення ідей, що стосуються нервової діяльності».

Згідно з теорією Мак-Каллока і Піттса, виведення даних

від нейрона має математичне значення, що дорівнює зваженій

сумі введень. Хоч і було доведено, що ці прості нейрони

можуть бути відмінними обчислювальними пристроями, коли

використовуються відповідні ваги, відчувалася відсутність

універсального правила навчання, тобто методу для

регулювання ваг у нейрон-них функціях.

Одне з найзнаменитіших правил (законів) навчання було

запропоновано 1949 року Дональдом Геббом (Donald Hebb). У

цьому правилі стверджується, що з більшою частотою сприяє

збудженню одного нейрона перша секунда, тобто

ефективнішим буде вплив на першій секунді. Отже, пам'ять

зберігається в синап-тичних зв'язках мозку, і навчання

відбувається зі змінами в силі цих зв'язків.

Першим нейрокомп'ютером (neurocomputer) можна

вважати пристрій «Snark», який розробив М. Мінський

(Marvin Minsky) на початку 50-х років XX ст., що

розглядається багатьма вченими як перший комп'ютерний

аналог людського мозку. Хоча з технічного боку пристрій мав

певний успіх, проте він був неспроможним виконати будь-яку

значну функцію з оброблення інформації.

У середині 50-х років Франк Розенблат (Frank Rosenblatt),

нейрофізик з університету Cornell (США), розробив пристрій

апаратних засобів персептрон (Perceptron) — електронний

пристрій для розпізнавання зорових образів (зображень). В

персепт-роні використані штучні нейронні структури, які

Розенблат назвав персептронами, комбінованими з простим

правилом навчання. Персептрон міг узагальнювати й

реагувати на незнайомі ввідні стимули. Хоч успіх Розенблата і

сприяв появі надій на швидке створення штучного мозку,

проте М. Мінський і С. Па-перт (Seymour Papert), піонери в

галузі штучного інтелекту, довели, що персептрони

Розенблата не зможуть розв'язати прості проблеми логіки, що

послужило тимчасовим гальмом дослідження нейромереж.

Реальні досягнення щодо створення та широкого застосування

нейромереж отримані за останні десять років.

Сучасні інструментальні засоби нейромереж

використовуються для сприймання інформації за допомогою

вивчення взірців (шаблонів) і потім застосовування їх з метою

передбачення майбутніх зв'язків або відношень. Нейромережі

є найзагальнішим типом методики дейтамайнінгу, причому

деякі люди навіть вва-

420

нэть, щ

використання нейромереж є єдиним типом дейтамай-

нінгу. Продавці нейромережевих програмних продуктів часто

використовують багато необгрунтованих рекламних тверджень

стосовно можливостей нейромереж. Одним із таких тверджень, яке

є особливо сумнівним, є те, що нейромережі можуть компенсувати

низьку якість даних.

Нейромережі навчаються створювати взірці безпосередньо з

даних за допомогою повторного їх вивчення, щоб ідентифікувати

зв'язки і побудувати модель. Вони будують моделі методом проб і

помилок. Мережа підбирає значення параметра шляхом зіставлення

з фактичною величиною. Якщо приблизна оцінка вихідного

параметра неправильна, то модель регулюється. Цей процес

включає три ітеративні кроки: передбачення, порівняння і при-

стосування (або корегування). Нейромережі досить просто засто-

совуються в СППР з метою класифікування даних і для передба-

чень. При цьому вхідні дані комбінуються і зважуються, на основі

чого генеруються вихідні значення.

Передусім, коли йдеться про нейронні мережі, то частіше ма-

ються на увазі штучні нейронні мережі. Деякі з них моделюють

біологічні нейронні мережі, а деякі — ні. Однак історично склалося

так, що перші штучні нейронні мережі були створені внаслідок

спроб створити комп'ютерну модель, що відтворює діяльність

мозку в спрощеній формі. Звичайно, можливості людського мозку

незмірно більші, ніж можливості самої потужної штучної нейронної

мережі.

Сучасні нейромережі мають низку властивостей, характерних

для біологічних нейромереж, у тому числі й людського мозку.

Головна їх властивість — здібність до навчання. Для розв'язання

якої-небудь задачі на комп'ютері традиційним методом необхідно

знати правила (математичні формули), за якими зі вхідних даних

можна отримати вихідні, тобто знайти розв'язок задачі. А за

Допомогою нейромережі можна знайти розв'язок, не знаючи пра-

вил, а маючи лише кілька прикладів.

Нейромережі використовують підхід до розв'язання задач

ближчий до людського, ніж традиційні обчислення. Дійсно, на-

приклад, коли людина переходить вулицю, вона оцінює швидкість

руху автомобіля, виходячи з попереднього досвіду, не ви-

користовуючи математичних обчислень. Або, наприклад, як Дитина

без великих зусиль може відрізнити кішку від собаки, або Дівчинку

від хлопчика, ґрунтуючись на раніше бачених прикладах. При

цьому часто вона не може точно сказати, за якими ознаками вона їх

відрізняє, тобто дитина не знає чіткого алгоритму.

421

Інша важлива властивість нейромереж — здатність

знаходити розв'язки, ґрунтуючись на змішаних, загальних,

спотворених і навіть суперечливих даних. Ще одна чудова

властивість — ц

стійкість до відмов у функціонуванні. У разі

виходу з ладу частини нейронів, уся мережа загалом

залишається працездатною, хоча, звичайно, точність

обчислень знижується.

9.4.2. Застосування нейронных мереж

Поява і широке застосування останнім часом

нейромереж і нейрокомп'ютерів зумовлено низкою важливих

підстав. По-перше, дуже багато задач з інформатики та

економіки не можна розв'язати класичними методами теорії

управління, оптимі-зації і системного аналізу. Річ у тім, що

будь-який проектувальник складних систем має справу з тим

самим комплексом проблем, що погано піддаються

розв'язанню традиційними методами. Неповнота знань про

зовнішній світ, неминуча погрішність даних, які надходять,

непередбачуваність реальних ситуацій — усе це змушує

розробників мріяти про адаптивні інтелектуальні системи, які

здатні підстроюватися до змін у «правилах гри» і самостійно

орієнтуватися за складних умов.

По-друге, «прокляття розмірності» стає реальним стримую-

чим чинником за розв'язання багатьох (якщо не більшості)

серйозних задач. Проектувальник не в змозі врахувати і звести

в загальну систему рівнянь всю сукупність зовнішніх умов,

особливо за наявності безлічі активних протидій. Тому

самостійна адаптація системи в процесі динамічного

моделювання «умов, наближених до бойових» — чи не

єдиний спосіб розв'язування задач за таких обставин.

Нейромережі (нейрокомп'ютери) забезпечують

користувачів надзвичайно гнучким і в певному розумінні

універсальним аналітичним інструментарієм. Вони дають

змогу розв'язувати досить різні типи задач. Охарактеризуємо

деякі з них.

Класифікація образів. Завдання полягає у визначенні

належності вхідного образу (наприклад, мовного сигналу або

рукописного символа), поданого вектором ознак, одному або

кільком заздалегідь визначеним типам. До відомих додатків

відносяться розпізнавання букв, розпізнавання мови,

класифікація сигналу електрокардіограми, класифікація

клітин крові тощо.

Кластеризація/категоршація. За розв'язання завдання з

кластери-зації, яке відоме також як класифікація образів «без

учителя», відсу-

422

тНЯ

навчальна вибірка з мітками типів. Алгоритм кластеризації

ґрунтується на подібності образів і розміщує схожі образи в

один кластер. Відомі випадки застосування кластеризації для

добування знань, стиснення даних і дослідження їх

властивостей.

Апроксимація функцій. Допустимо, що є навчальна вибірка

(х

уі), (хг, Уг) ••, (х„, Уп) (пари відповідних даних входу-

виходу), яка генерується невідомою функцією F(x),

спотвореною шумом. Завдання апроксимації полягає в

знаходженні оцінки невідомої функції F(x). Апроксимація

функцій необхідна за розв'язання численних інженерних і

наукових завдань з моделювання.

Передбачення/прогнозування. Нехай задані п дискретних

значень \y(t\), y{h)..., y{t

)} у послідовні моменти часу % Гг,...,

?„. Завдання полягає в прогнозуванні значення у (t„+ 1) в

деякий майбутній момент часу t

+ 1. Передбачення мають

значний вплив на прийняття рішень у бізнесі, науці і техніці.

Прогноз цін на фондовій біржі і прогноз погоди є типовими

додатками методів передбачення/прогнозування.

Оптимізація. Численні проблеми в економіці та інших

наукових галузях можуть розглядатися як проблеми

оптимізації. Завданням алгоритму оптимізації є знаходження

такого розв'язку, який задовольняє систему обмежень і

максимізує або мінімізує цільову функцію.

Контекстно-адресована пам'ять. У моделі обчислень фон

Неймана, що послужила базисом традиційної обчислювальної

техніки, звернення до пам'яті було можливим тільки за

допомогою адреси комірки пам'яті, яка не залежить від її

змісту. Більше того, якщо допущена помилка в адресі, то може

бути знайдена абсолютно інша інформація. Контекстно-

адресована (асоціативна) пам'ять або пам'ять, що адресується

за змістом, доступна за вказівкою заданого змісту.

Асоціативна пам'ять надзвичайно бажана за створення

мультимедійних інформаційних баз даних.

Управління. Розглянемо динамічну систему, задану

сукупністю {и(0, у(і)}, де u(t) є вхідним керуючим впливом, a

y(t) — виходом системи в момент часу t. У системах

управління з еталонною моделлю мети управління є

можливість розрахунку такої величини вхідного впливу u(t),

при якій система рухається за бажаною траєкторією, що

визначається еталонною моделлю.

У принципі, нейронні мережі можуть обчислювати

значення будь-яких функцій, інакше кажучи, виконувати все,

що можуть робити традиційні комп'ютери. На практиці для

того, щоб застосування нейронної мережі було доцільним,

необхідно, щоб задача мала такі ознаки: невідомий алгоритм

або принципи розв'язання

423

задачі, але накопичена достатня кількість прикладів;

проблема характеризується великими обсягами вхідної

інформації; дані неповні або надмірні, містять шуми, частково

суперечливі.

Отже, нейронні мережі добре підходять для розпізнавання

образів і розв'язання задач з класифікації, оптимізації і

прогнозування. Нижче наведений перелік можливих

застосувань нейрон-них мереж у промисловості, на базі яких

або вже створені комерційні продукти, або реалізовані

демонстраційні прототипи.

Банки і страхові компанії, автоматичне зчитування чеків і

фінансових документів; перевірка достовірності підписів;

оцінювання ризику для позик; прогнозування змін

економічних показників.

Адміністративне обслуговування: автоматичне зчитування

документів; автоматичне розпізнавання штрихових кодів.

Нафтова і хімічна промисловість: аналізування

геологічної інформації; ідентифікація зіпсувань обладнання;

розвідування покладів мінералів за даними аерофотознімків;

аналіз складу домішок; управління процесами.

Військова промисловість і аеронавтика: оброблення

звукових сигналів (поділ, ідентифікація, локалізація, усунення

шуму, інтерпретація); оброблення радарних сигналів

(розпізнавання цілей, ідентифікація і локалізація джерел);

оброблення інфрачервоних сигналів (локалізація);

узагальнення інформації; автоматичне пілотування.

Промислове виробництво: керування маніпуляторами;

управління якістю; управління процесами; виявлення

зіпсувань; адаптивна робототехніка; керування голосом.

Служба безпеки: розпізнавання осіб, голосів, відбитків

пальців.

Біомедична промисловість: аналіз рентгенограм;

виявлення відхилень в електрокардіограмах.

Телебачення і зв'язок: адаптивне управління мережею

зв'язку; стиснення і відновлення зображень.

Можна продовжувати наведення прикладів вдалого

використання технологій нейронних мереж. Проте є низка

недоліків, пов'язаних із застосуванням для розв'язання задач з

ідентифікації взірців інформації. Головним із них є те, що для

навчання нейро-мережі потрібна велика кількість фактичної

інформації (кількість спостережень від 50 до 100). Для

аналітичних задач у бізнесі це не завжди можна забезпечити.

Крім цього, неявне навчання призводить до того, що

структура зв'язків між нейронами стає «незрозумілою» — не

існує іншого способу її прочитати, крім як запустити

функціонування мережі. Стає складно відповісти на

запитання: «Як нейронна мережа отримує результат?»— тобто

побудувати зрозумілу людині логічну конструкцію, що відтво-

424

рює дії мережі. Це явище можна назвати «логічною

непрозорістю» нейронних мереж, навчених за неявними

правилами. Навіть добре натренована нейромережа являє

собою «чорний ящик», тобто систему, в якій зовнішньому

спостерігачеві доступні лише вхідні та вихідні величини, а

внутрішня будова її та процеси, що в ній перебігають,

невідомі.

9.4.3. Біологічні нейрони і нейромережі

Як уже зазначалося, ідея створення проекту штучних

нейронних мереж виникла внаслідок бажання штучно

відтворити процеси мислення людського мозку. Нервова

система і мозок людини складаються з нейронів, сполучених

між собою нервовими волокнами. Нервові волокна здатні

передавати електричні імпульси між нейронами. Всі процеси

передавання подразнень від нашої шкіри, вух і очей до мозку,

процеси мислення й управління діями — все це реалізоване в

живому організмі як передавання електричних

(електрохімічних) імпульсів між нейронами.

Компонентою мозку, яка забезпечує можливість

оброблення інформації, є нейрон (neuron), який складається з

трьох основних зон: дендритів (dendrites) — відгалужень

нервових клітин, що проводять нервовий імпульс до клітини,

сома (soma) — тіла нейрона і аксона (axon) (інші назви

аксона: неврит, нейрит) — відростка нервової клітини, по

якому проходять нервові імпульси від клітин. Дендрити

виконують функцію введення електричних (електрохімічних)

сигналів, сома оброблює сигнали, і аксони утворюють вихідні

маршрути для оброблених сигналів. Рис. 9.9 ілюструє модель

окремого біологічного нейрона.

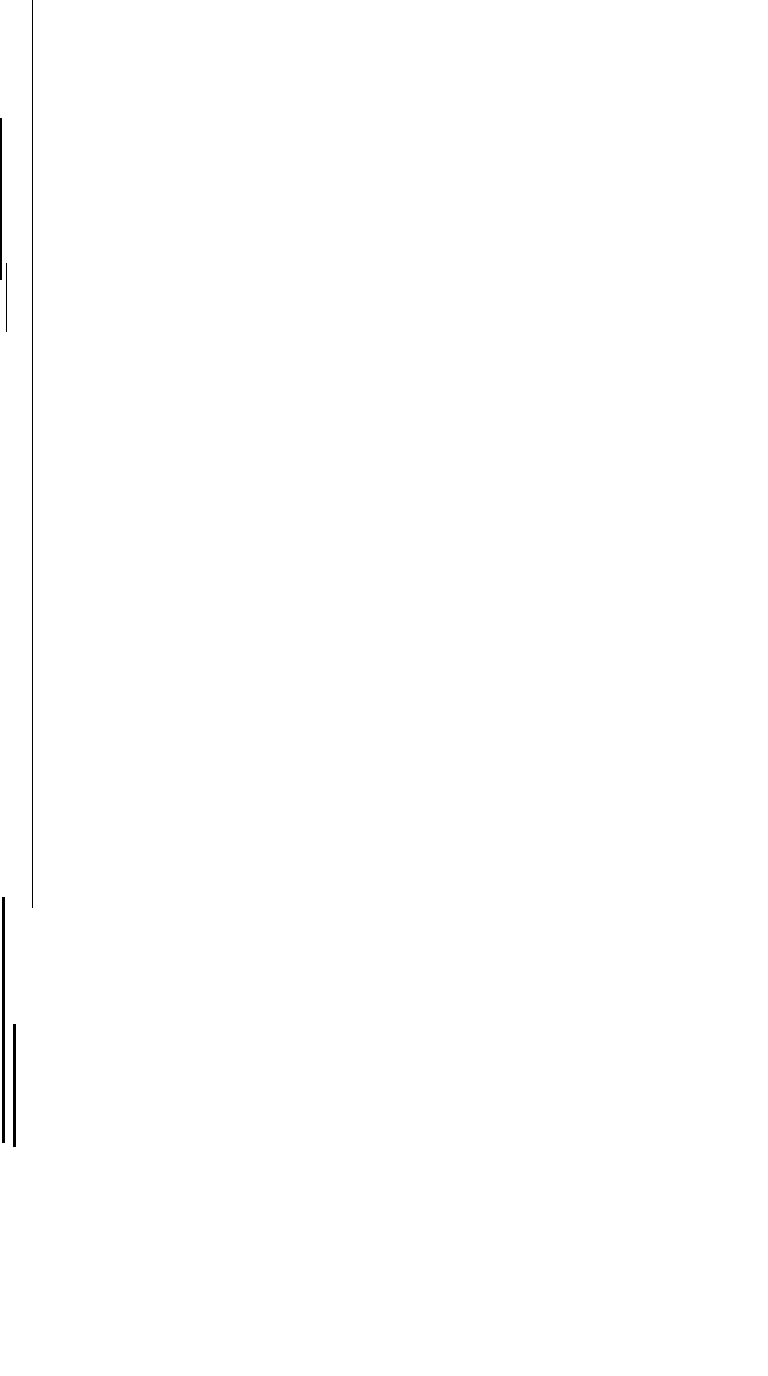
Як видно із рисунка, кожний нейрон має паростки

нервових волокон двох типів — дендрити, які приймають

імпульси, і єдиний аксон, через який нейрон може передавати

імпульси. Аксон контактує з дендритами інших нейронів

через спеціальні утворення — синапси, які впливають на силу

імпульсу. Сила зв'язку синапсового з'єднання між аксоном

збудженого (активізованого) нейрона і дендритами

отримуючого нейрона визначає вплив імпульсу.

Через цей дуже простий механізм вхідним сигналам від

сусідніх нейронів можна присвоювати пріоритети або

коефіцієнти важливості щодо процесів акумуляції сигналів

сомами. Ці пріоритети мають подібне призначення, як

запам'ятовуючий пристрій чи пам'ять у мережі.

Хоч тривалість відповіді для окремого нейрона приблизно

в тисячу разів повільніша, ніж цифрова комутація в

комп'ютері, мозок здатний до розв'язання комплексних

проблем, як наприклад, бачення і мови. Це забезпечується за

допомогою поєднання величезної кількості повільних

нейронів (процесорів) у безмірно велику комплексну мережу.

Кількість нейронів у людському мозку приблизно дорівнює

і6

, І кожний із них формує приблизно 104 синапси з іншими

нейронами. Це є прикладом паралельного розподіленого

оброблення інформації (parallel distributed processing— PDP),

яке уможливлює кожне завдання поділити на безліч

субзавдань, що виконуються одночасно.

Можна вважати, що в результаті проходження через синапс

сила імпульсу змінюється в певну кількість разів, яку будемо

називати вагою синапса. Імпульси, що поступили до нейрона

одночасно через кілька дендритів, підсумовуються. Якщо

сумарний імпульс перевищує деяку порогову величину, то

нейрон збуджується (рівень калію в ньому досягає критичної

межі), формує власний імпульс і передає його далі через

аксон. Важливо зазначити, що ваги синапсів можуть

змінюватися згодом, а отже змінюватиметься і поведінка

відповідного нейрона.

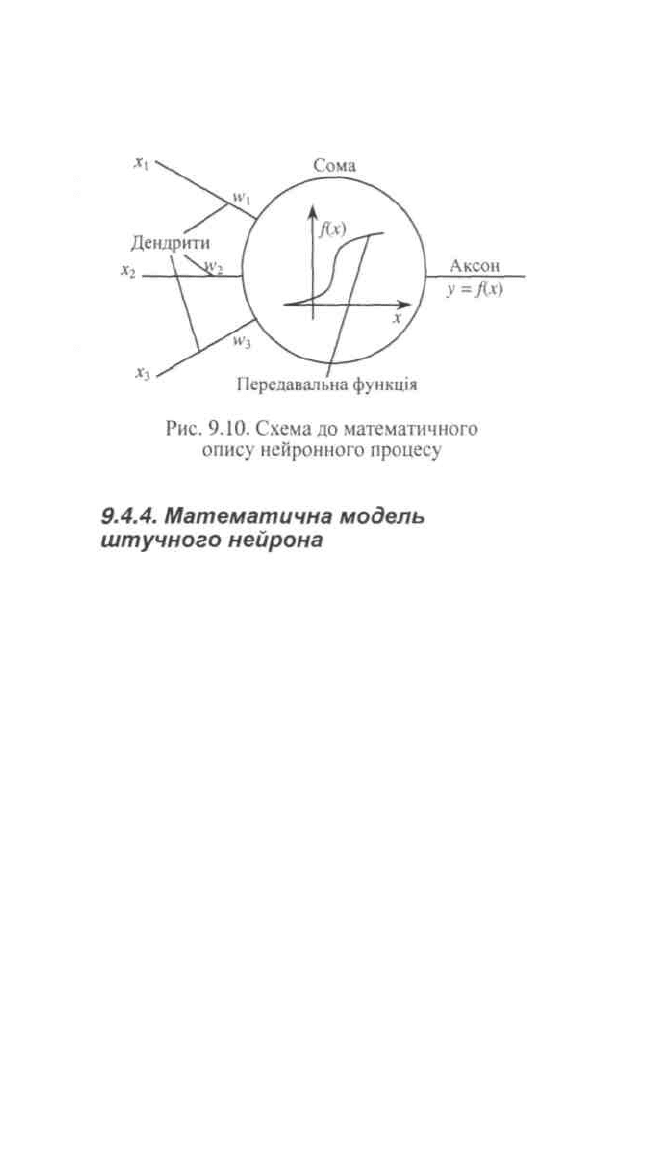
Неважко побудувати математичну модель описаного

процесу. На рис. 9.10 зображена схема нейрона з трьома

входами (дендритами), причому синапси цих дендритів мають

ваги w\, wi, .

Нехай по синапсах поступають імпульси силами відповідно

х\, Хг, хт,, тоді після проходження синапсів і дендритів до

нейрона поступають імпульси w\X\, W2X2, изд- Нейрон

перетворює отриманий сумарний імпульс (функцію стану) х =

w\X\ + изд + wyXi відповідно до деякої передавальної функції

f(x). Силу вихідного імпульсу можна обчислити за формулою:

у = f(x)=f(w\X\ + м?гхг +

426

+ муХз)- Отже, нейрон повністю описується своїми вагами

, що визначають функцію стану, і передавальною функцією/

(х). Функцію fix) інколи називають функцією активації або

функцією перетворення. Отримавши ряд імпульсів (вектор)

на вході, нейрон передає деякий імпульс (число) у на виході.

Штучні нейронні мережі не є точними копіями

біологічної системи людського мозку, проте вони

відтворюють такі здатності людини, як узагальнення,

навчання, абстрагування і навіть інтуїцію. Все залежить від

того, наскільки вдало вибрана математична модель нейронів і

структура взаємозв'язків між окремими нейронами в

нейромережі. Причому слід зауважити, що немає єдиного

підходу до побудови нейромереж, конструкція їх значною

мірою залежить від уміння авторів штучно відтворити функції

біологічного нейрона: від правильності оцінювання вхідних

значень, визначення стану нейрона, адекватності передава-

льної функції вихідному імпульсу.

Математична модель штучного нейрона (далі — нейрона)

має структуру, яка тією чи іншою мірою відтворює описану

математичну модель біологічного нейрона. Введемо такі

позначення: N— загальна кількість нейронів у нейромережі; j

— індекс нейрона (/' = 1,2,..., N); n — кількість входів у j-ий

нейрон 0=1,2,..., tij); x

j— значення сили імпульсу /-входу в у'-

нейрон;

ij ■— вага імпульсу /-входу ву'-нейрон.

427

товуючи готові нейропакети (наприклад, нейропакет BrainMaker

американської фірми «California Scientific Software»), усі ці функції

максимально автоматизовані, користувачеві потрібно задати пише

кількість параметрів задачі (вимірність простору) і програма

автоматично вибере необхідну мережу, потім вибрати низки даних

(наприклад, в електронній таблиці Excel) для навчання і тестування та

виконувати інструкції в інтерактивному режимі.

9.4.5. Архітектура нейромереж

У процесі розроблення нейромереж автори наділяють

штучні нейрони різноманітними властивостями з тим, щоб

комп'ютерні нейромережі адекватно відображали можливості

біологічних нейромереж стосовно розв'язання певного типу проблем,

що зумовило появу великого різноманіття підходів до алгоритмів

нейромереж, зокрема штучні нейрони можуть бути з різними

передавальними функціями, з різними функціями стану, двійковими,

цілочисельними, дійсними та іншими числовими значеннями входів і

ваг. Тому в термінах нейронних мереж можна описувати алгоритми

розв'язання як добре формалізованих задач, наприклад задач

математичної фізики, так і задач розпізнавання, що погано

формалізуються, класифікації, узагальнення і асоціативного

запам'ятовування.

Мережі можуть бути такими, що конструюються або що на-

вчаються. У мережі, що конструюється, кількість і тип нейронів,

граф міжнейронних зв'язків, ваги входів нейронів визначаються за

створення мережі, виходячи із задачі, що розв'язується. Наприклад, за

конструювання мережі Хопфілда, що функціонує як асоціативна

пам'ять, кожна вхідна послідовність із заздалегідь визначеного

певного ряду бере участь у визначенні ваги входів нейронів мережі.

Після етапу конструювання функціонування мережі полягає в

наступному. За подачі на входи часткової або помилкової вхідної

послідовності мережа через якийсь час переходить в один зі стійких

станів, передбачених за її конструювання. При цьому на входах

мережі з'являється послідовність, що визнається мережею як

найближча до спочатку поданої. Кількість вхідних послідовностей —

М, що запам'ятовуються, пов'язана з кількістю нейронів у мережі

співвідношенням: M<N/41ogN, де N — кількість нейронів.

У мережах, що навчаються, графи міжнейронних зв'язків і ваги

входів змінюються за виконання алгоритму навчання. За алго-

429