Шпоры по оптике
Подождите немного. Документ загружается.

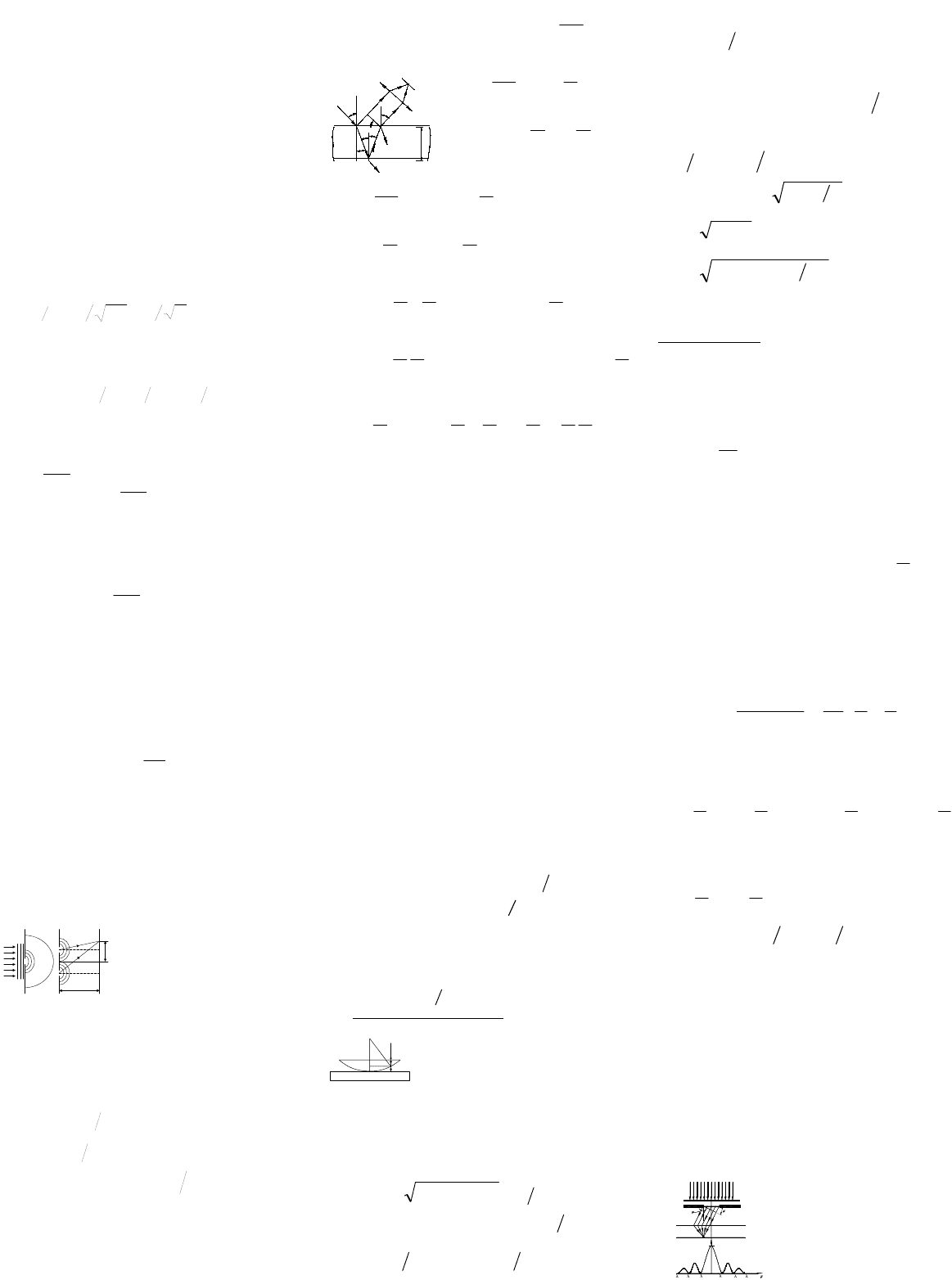
1. Развитие представлений о природе света. Корпускулярно-волповой
дуализм. Уравнение плоской волны, ее характеристики. Когерентность.
Свет – поток частиц-корпускул (твердых шариков). Красный свет –
большие шарики, фиолетовый – малые. Известные тогда явления света:
отражение, преломление, дисперсия – этой теорией объяснялись. В тоже
время Гук выдвинул волновую теорию. Свет – волна в среде. Эта теория
тоже объясняла известные тогда оптические явления. Изучаются явления
интерференции, дифракции и поляризации света. Эти явления объясняются
только волновой теорией. Поскольку явления отражения, преломления и
дисперсии тоже можно объяснить волновой теорией. Триумфом волновой
теории стал 1861 год, когда Максвелл обосновал электромагнитную теорию
света. Казалось, что в оптике все сделано, все объяснено. Но в конце 19 и
вначале 20 века было открыто явление теплового излучения абсолютно
черного тела, эффект Комптона, фотоэффект. Не смотря на все усилия
физиков, волновая теория не смогла объяснить эти явления.
Волновая оптика изучает оптические явления, считая свет электромагнитной
волной. Оптика рассматривает часть излучений воспринимаемых глазом –
видимый свет. Длина волны
меняется от 380нм до 770нм
мнм
9
101
. Свет с длинами волн
380
нм называется ультрафиолетовым, с
770
нм – инфракрасным.
Характерным свойством излучения является частота, которая не зависит от
среды. Длина волны от среды зависит. При переходе из одной среды в
другую меняется скорость света и поэтому меняется длина волны.
Скорость света в среде равна:
ccnc
, где n - показатель
преломления среды,
- электрическая, а
- магнитная
проницаемость среды. Для большинства сред
1
.
Длина волны в среде равна:
nnvcT
ср
, где
-
длина волны в вакууме.
Волны, имеющие одинаковую частоту и постоянную во времени разность
фаз называются когерентными.
Уравнение волны:
kxtEE
cos
0
;
2. Интерференция света. Условие максимума и минимума для разности
фаз и разности хода.
Интерференцией света называется наложение двух и более когерентных
волн, в результате чего происходит перераспределение энергии светового
потока в пространстве и наблюдаются интерференционные максимумы и
минимумы.
Волны, имеющие одинаковую частоту и постоянную во времени разность
фаз называются когерентными.
Разность фаз равна:
L
0
2
Разность хода:
12
LLL
, где
- длина волны в вакууме, а
L
- оптическая разность хода.
Если
0
mL
(m=0,1,2,3,…) ,то
m2
и колебания будут происходить в один. фазе =>
это условие максимума.
Если
2
12
0
mL
(m = 0,1,2,3,…) то,
12 m
и колебания будут происходить в
противофазе => это условие минимума.
Если в оптической разности хода укладывается нечетное число полуволн, то
наблюдается интерференционный минимум.
3. Опыт Юнга. Рассчитать интерференционную картину от 2-х
источников.
Юнг получил полосы интерференции способом – пучок света от солнца
падал на экран с малым отверстием или узкой щелью. Затем на экран с
двумя узкими отверстиями S1 и S2. Световые пучки от S1 и S2
накладывались, в результате чего получается 2 перекрещивающихся,
расходящихся когерентных пучка света. На экране в месте перекрывания
пучков наблюдались параллельные интерференционные полосы.
l
d
O
A
x
r
1
r
2
S
1
S
2
d- расстояние между источниками,
-
расстояние от источников до экрана,
x
- расстояние от точки О до
рассматриваемой точки А.
Интенсивность в любой точке А определяется оптической разностью хода:
121122
rrrnrnL
, так как
1
21
nn
.
Из рисунка следует, что
2
2
2
2
2 dxr
,
2
2
2
1
2 dxr
, тогда
xddxdxdxdxrr 244
22222
1
2
2
xdrrrr 2
1212
2
12
rr
, так как
d
,
12
rr
.
12
rrL
,
xdL 22
,
xd
L
.
Найдем координаты максимумов:
2
2
m
xd
L
,
отсюда
2
2
max
m
d
x
,
координаты минимумов:
2
12
m
xd
L
, отсюда
2
12
min
m
d
x
.
Расстояние между соседними максимумами равно:
d
mm
d
x
1
2
2
max
,
а между соседними минимумами:
d
mm
d
x
12112
2
min
.
Расстояние между соседним максимумом и минимумом:
22
2
2
12
d
m
d
m
d
x
4. Интерференция в тонких пленках. Кольца Ньютона. Получить
выражение для радиуса темных колец.
Явление интерференции в тонких пленках широко наблюдается в
естественных условиях: радужная окраска мыльных пузырей, нефтяных
пленок, масляных пятен на поверхности воды, крыльев бабочки.
В этом случае интерферируют лучи, полученные от отражения
падающего луча от верхней и нижней поверхностей. Оптическая разность
хода между лучами не велика из-за малой толщины пленки и поэтому они
принадлежат одному цугу, а значит когерентны.
Падающая волна частично отражается от поверхности пленки (луч 1) и
частично преломляется (луч OC). Преломленная волна, достигнув нижней
поверхности пленки, отражается от нее (луч CB). Луч CB затем
преломляется на верхней поверхности (луч 2). Лучи 1 и 2 с помощью линзы
собираются на экране в точке P и интерферируют. Результат интерференции
зависит от оптической разности хода между лучами 1 и 2.
Оптическая разность хода между двумя интерферирующими
лучами от точки O до плоскости AB равна:
2
OAnCBOCL
, где
n
- показатель преломления пленки, член
2
обусловлен
потерей полуволны при отражении света от границы раздела с оптически
более плотной средой. Расстояния OA, OC и CB находится геометрическим
методом (
r
, рис.1):
sin2sin dtgOBOA
,
cosdCBOC
.
Установка для наблюдения колец Ньютона состоит из плоско-
параллельной пластины и плосковыпуклой линзы большого радиуса
кривизны. Свет на установку падает вертикально (рис. 4).
r
m
d
m
R
R
1
2
(рис.4) Тонкая пленка образуется между линзой и
пластинкой. Это воздушная пленка или жидкая. Пленка имеет вид клина.
Поэтому возникают полосы равной толщины. Из-за симметрии они имеют
вид окружностей.
Рассмотрим ход одного из лучей. Поскольку угол клина мал, можно
считать, что угол падения везде ноль. Когерентными являются лучи,
отразившиеся в точках 1 и 2. В точке 1 они накладываются. Найдем радиус
m-ого кольца
m
r
.
Оптическая разность хода между лучами 1 и 2 равна:
2sin2
22
ndL
m
. В нашем
случае
0
, поэтому:
22
ndL
m
.
Предположим, что кольцо темное, тогда
21222
mnd
m
. Отсюда
выражаем толщину клина в точке
m
кольца
m
d
:
nmd
m
2
.
Из рис.4 следует, что
2
2
2
mm
rdRR
.
Пренебрегая членом
2
m
d
, получаем:
Rrd
mm
2
2
.
Приравнивая оба выражения для
m
d
, получаем:
Rrnm
m
22
2
. Отсюда выражаем радиус
m
-
ого темного кольца:
nmRr
m
.
Для воздушной пленки (n=1), это выражение принимает вид:
mRr
m
.
Радиусы светлых колец:
nRmr
m
212
5. Дифракция света. Принцип Гюйгенса-Френеля.
Дифракция света – это явление отклонения волн от прямолинейного
распространения, явление огибания волнами препятствий и проникновения
волн в область геометрической тени.
Принцип Гюйгенса-Френеля:
1)Каждая точка фронта волны является источником сферических
когерентных волн.
2)Световой эффект в точке наблюдаемый на экране, определяется
интерференцией вторичных волн.
6. Метод зон Френеля. Дифракция Френеля на диске.
Для упрощения расчета результата интерференции большого числа волн
используется метод зон Френеля. Фронт световой волны делят на области
(зоны) так, что оптическая разность хода
l волн, пришедших в некоторую
точку экрана от соседних зон, равна /2; в этом случае разность фаз этих
волн равна
l2
, т.е. волны будут гасить друг друга и точка экрана не
будет освещена. Если волны распространяются в воздухе, то оптическая
разность хода будет равна разности расстояний, пройденных этими волнами.
Дифракция Френеля на небольшом диске.
В этом случае диск закрывает
m
первых зон Френеля.
Амплитуда результирующего колебания в точке
M
равна:
13211321
2
1
...
2
1
2
1
2
1
...
mmmmmmmm
AAAAAAAAA
Итак, в случае диска в точке M всегда будет светлое пятно,
окруженное концентрическими темными и светлыми кольцами, а
интенсивность в максимумах убывает с расстоянием от центра картины.
7. Дифракция Френеля на круглом отверстии.
Поставим на пути света от источника непрозрачный экран с круглым
отверстием. Дифракционная картина наблюдается на экране, параллельном
плоскости отверстия и находящимся от него на расстоянии b. Выясним, что
будет наблюдаться в точке M, лежащей напротив центра отверстия.
Отверстие открывает m зон Френеля. Зная радиус отверстия можно найти
значение m:
ba
r
ab
bar
m
mm
11
22
.
Амплитуда результирующего колебания в точке M равна:
m
AAAAA ...
321
Если m- нечетное, то
m
AAAAAA
2
1
...
2
1
2
1
2
1
3211
Если m мало, то
m
AA
1
и
1
AA
.
Если m- четное,
0
2
1
2
1
11
mm
AAAA
.
В общем случае
22
1 m
AAA
, где знак «+»
соответствует нечетным m, а «-»- четным.
Как видно из формулы число зон Френеля
m
зависит от
расстояния экрана до перегородки b. Поэтому, перемещая экран, в точке M
будет наблюдаться то светлое пятно (m- нечетное), то темное (m- четное).
Расчет амплитуды колебаний в других точках экрана более сложно.
8. Дифракция Фраунгофера на щели. Условие максимума и минимума.
Пусть на щель шириной
aMN
падает
монохроматический свет с длиной
волны
. Из-за дифракции свет
после щели распространяется во всех
направлениях. Лучи, которые идут не
отклоняясь, собираются линзой в
точке D (экран находится в
C
I
r
i
r
r
B
O
n
â
=1
n
A
1
2
P
d
2
2
или
T
2
k
1.0
0.047
0.017
0.047
0.017
0
+ /a
+2 /a +3 /a
sin
B
B0
D
C
NM
Ý
+3 /a +2 /a
+ /a
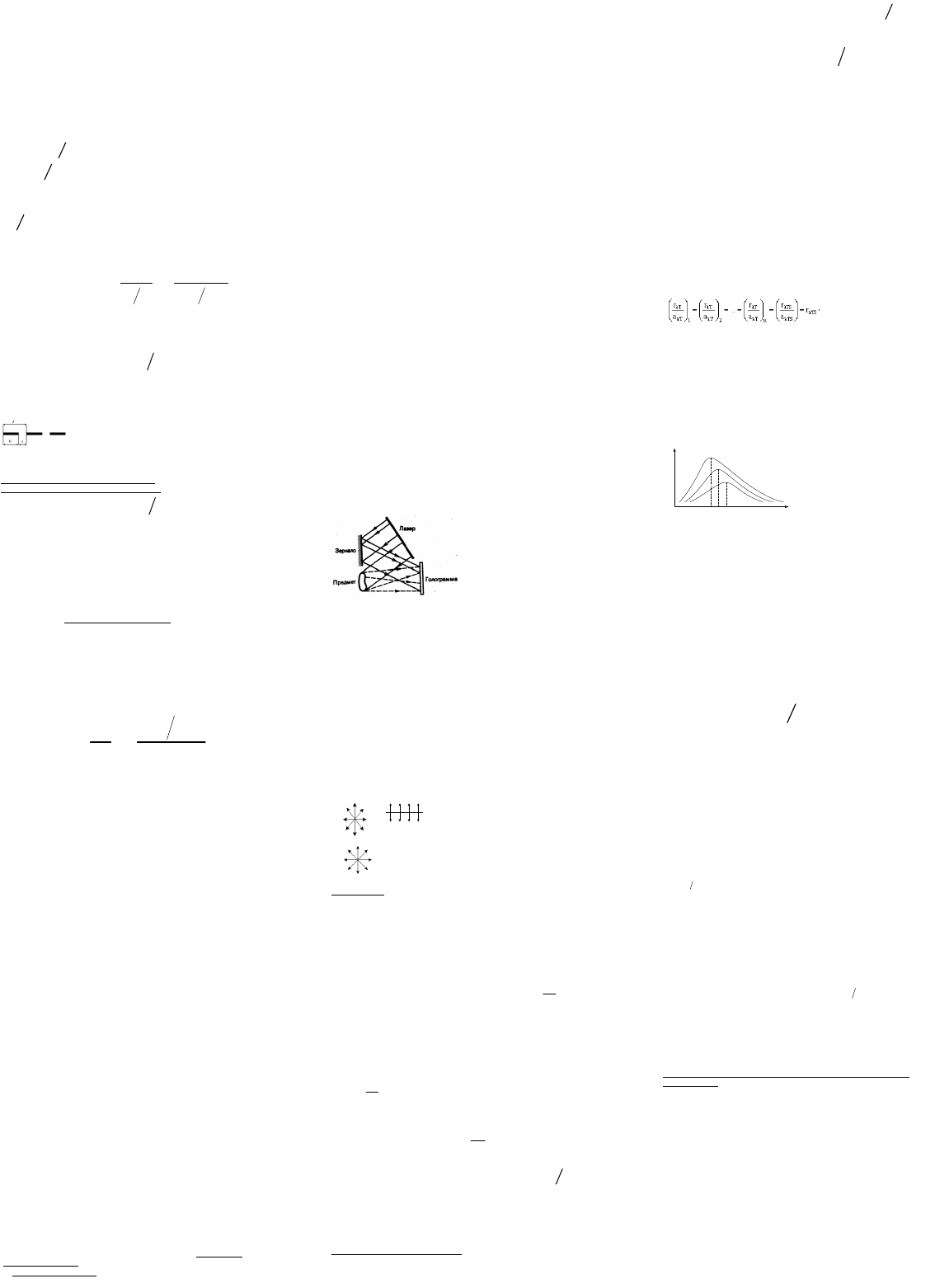
фокальной плоскости линзы). Точка D - главный фокус линзы. Рассмотрим
лучи, которые дифрагируют под углом
. Они соберутся на экране в
некоторой точке B (побочном фокусе линзы). Лучи, дифрагирующие под
другими углами, соберутся в других точках на экране. В итоге экран будет
освещен во многих местах, на нем будет чередование света и тени. Окажется
в точке B минимум или максимум зависит от разности хода поступающих
сюда волн. Щель является волновой поверхностью. По принципу Гюйгенса
каждая точка ее есть источник вторичных волн. Найдем разность хода волн,
приходящих в точку B. Для этого проведем фронт волны BD. Точный расчет
показывает, что оптические пути MB и FB одинаковы (геометрически путь
FB короче, но здесь толще линза). Поэтому разность хода лучей 1 и 2 равна
NFL
. Проведем систему плоскостей параллельных MF на
расстоянии
2
друг от друга. Разность хода разделиться на участки
длиной
2
, а щель на полоски, называемые зонами Френеля.
Площади этих зон одинаковы, поэтому по принципу Гюйгенса-Френеля
они испускают волны равной интенсивности. Разность хода между
соответствующими точками соседних полосок по построению равна
2
. Поэтому, если в щели укладывается четное число зон Френеля,
они попарно друг друга погасят. Тогда в точке B будет наблюдаться
минимум, если нечетное, то одна зона окажется непогашенной и в точке B
будет максимум.
Число зон Френеля равно
2
sin
2
aNF
. Если это
число четное, то мы получаем условие минимума:
ma
sin
,
если нечетное, то условие максимума:
212sin
ma
.
9. Дифракционная решетка. Условия главных максимумов и
минимумов.
Дифракционная решетка – это система одинаковых параллельных
щелей, разделенных равными промежутками.
Величина
bad
называется постоянной
дифракционной решетки.
Условие главных максимумов для решетки:
md
sin
А условие главных минимумов для решетки:
212sin
md
.
10. Дисперсия света. Нормальная и аномальная дисперсия.
Дисперсией света называется зависимость показателя преломления
n вещества от частоты
v
или от длины волны
. В результате
дисперсии света происходит разложение белого света в спектр при
прохождении его через призму. Квадрат показателя преломления равен:.
22
00
2
0
2
1
m
en
n
Если в веществе имеются различные заряды
i
e
, совершающие
колебания с различными собственными частотами
i0
, то
k
i
i
ii
men
n
1
22
0
2
0
0
2
1
,
где
i
m
- масса
i
-ого заряда.
0
- собственная частота
колебаний электрона,
e
- заряд электрона,
Из последних выражений вытекает, что показатель преломления
зависит от частоты внешнего поля, то есть полученные зависимости
подтверждают явление дисперсии. На рис.2. приведен график зависимости
2
n
от
.
A
B
Рис.2.
В области от
0
до
0
,
2
n
больше
единицы и возрастает с увеличением
(нормальная дисперсия). При
0
,
2
n
. В области от
0
до
,
2
n
меньше единицы и возрастает от
до 1
(нормальная дисперсия). Стремление n вблизи собственной частоты
0
к бесконечности получилась в результате допущения об
отсутствии сил сопротивления при колебаниях электрона. Если учесть силы
сопротивления, то график функции
2
n
от
вблизи точки
0
задается штрихованной линией AB. Область AB - это область
аномальной дисперсии (
2
n
убывает при возрастании
).
11. Поглощение света. Закон Ламберта-Бугера.
Явление уменьшения энергии световой волны при ее распространении в
веществе, происходящее вследствие преобразования энергии
электромагнитного поля волны во внутреннюю энергию вещества или в
энергию вторичного излучения (фотолюминесценцию), имеющего другой
спектральный состав и направление распространения, называется
поглощением света.
Закон Бугера–Ламберта: Интенсивность света при прохождении через
поглощающую среду уменьшается по экспоненциальному закону:
axJJ exp
0
,
где
0
J
и
J
- интенсивности света на входе и выходе из слоя
толщиной x, a - показатель поглощения среды, который зависит от
химической природы и состояния вещества, и от длины волны
падающего света.
не зависит от интенсивности света.
12. Рассеяние света.
Рассеянием света называется явление преобразования света
веществом, сопровождающееся изменением направления распространения
света и проявляющееся как несобственное свечение вещества. Рассеяние
света по физическому содержанию представляет дифракцию волн на
неоднородностях среды.
Это свечение обусловлено вынужденными колебаниями электронов в
атомах, молекулах или ионов рассеивающей среды под действием
падающего света. Рассеяние света может возникнуть только в оптически
неоднородной среде, показатель преломления которой нерегулярно
меняется от точки к точке. Примеры таких сред – это мутные среды (дым,
туман, эмульсии, коллоидные растворы, матовые стекла), содержащие
мелкие частицы, показатель преломления которых отличается от показателя
преломления окружающей среды.
13. Основы голографии.
Голография – это особый способ записи на фотопластинке структуры
световой волны, отраженной предметом. При освещении голограммы
пучком света эта волна почти полностью восстанавливается и создается
впечатление, что наблюдается сам предмет. Обычный фотографический
способ получения изображения предмета основан на регистрации с
помощью фотопластинки различий в интенсивности света, рассеваемого
разными малыми элементами поверхности предмета. Но при этом не
учитывается расстояние, откуда идет свет. В результате получается плоское
изображение предмета. Распределение интенсивности в интерференционной
картине определяется как амплитудой интерферирующих волн, так и
разностью их фаз:
1221
2
2
2
1
2
cos2
AAAAA
. Свой метод Габор назвал
голографией.
Лазерный пучок делится на две части, одна его часть отражается зеркалом
на фотопластинку (опорная волна), а вторая попадает на фотопластинку,
отразившись от предмета (предметная волна). Опорная и предметная волны
когерентны и они интерферируют на фотопластинке. Интерференционная
картина, зафиксированная на фотопластинке после ее проявления,
называется голограммой предмета.
14. Поляризация света. Закон Малюса.
Доказательством поперечности световых волн является явление
поляризации света.
Световая волна состоит из множества цугов, испускаемых большим
числом атомов. Каждый цуг имеет случайную ориентацию векторов E и H, в
итоге в результирующей волне все направления равновероятны. Свет со
всевозможными равновероятными направлениями векторов E и H
называется естественным (скорость распространения направлена
перпендикулярно чертежу).
Свет, в котором одно из направлений колебаний светового
вектора
E
становится преимущественным, называется частично
поляризованным
Если колебания светового вектора происходят в одной
плоскости, то свет – плоско-поляризован.
Если конец вектора
E
описывает эллипс, то свет
эллиптически поляризован, если окружность, то
поляризован по кругу.
Закон Малюса: Интенсивность прошедшего света равна интенсивности
падающего света на угол между плоскостью колебаний падающего света и
плоскостью поляризатора.
2
0
cosJJ
.
Поставим на пути естественного света два поляризатора, плоскости
которых составляют угол
. Из первого поляризатора выйдет плоско-
поляризованный свет, интенсивность которого
ест
JJ
2
1
0
.
Согласно закону Малюса из второго поляризатора выйдет свет
интенсивности
2
0
cosJJ
. Интенсивность света,
прошедшего второй поляризатор равна:
2
cos
2
1
ест
JJ
.
Максимальная интенсивность, равная
ест
J
2
1
получается при
0
(поляризаторы параллельны). При
2
интенсивность равна нулю (скрещенные поляризаторы света не
пропускают).
15. Характеристики теплового излучения. Закон Кирхгофа.
Электромагнитное излучение, возникающее за счет внутренней
энергии тела и зависящее от температуры и оптических свойств этого тела,
называется тепловым излучением.
Характеристики теплового излучения.
Излучаемая телом энергия -
W
, измеряется в джоулях.
Мощность излучения или поток излучения
dtdW
-
определяется энергией излучаемой телом в единицу времени, измеряется в
ваттах. [Ф]=Дж/с=Вт.
Интегральная излучательность
sR
T
- физическая
величина, равная энергии, излучаемой в единицу времени с единичной
площади нагретого тела [R
T
]=Вт/м
2
. В этом определении имеется в виду
полная или интегральная энергия, излученная нагретым телом на всех
длинах волн.
T
r
- спектральная плотность излучательности это энергия, излучаемая
телом с единичной площади, в единицу времени в единичном интервале
длин волн вблизи данной длины волны
.
T
r
- зависит от T,
и
от природы вещества тела.
Зная
T
r
можно найти
T
R
:
drR
TT
.
Кирхгоф показал, что отношение спектральной плотности
излучательности
T
r
к спектральной плотности поглощательной
способности
T
a
для данных
и T одинаково для всех тел и
ровно спектральной плотности излучательности абсолютно черного тела
TS
r
:
(1)
Где
1a
TS
– поглощательная способность абсолютно черного тела.
Выражение (1) представляет закон Кирхгофа для теплого излучения. Из (1)
видно, чем больше
T
a
, тем больше
T
r
, поэтому абсолютно черное тело,
должно излучать больше, чем другие тела.
16. Закон Стефана-Больцмана.
Разлагая излучение абсолютно черного тела в спектр и измеряя
интенсивность излучения в разных участках спектра можно найти
зависимость спектральной плотности излучательности абсолютно черного
тела
TS
r
от длины волны при разных температурах (рис. 1).
T
1
T
2
T
3
m
m
m
T
1
T
2
T
3
> >
r
TS
Рис. 1.
Площадь, охватываемая кривой равна интегральной излучательности
абсолютно черного тела
TS
R
при соответствующих температурах.
Стефан и Больцман, анализируя экспериментальные данные, пришли к
выводу: Интегральная излучательность
абсолютно черного тела возрастает
пропорционально четвертой степени
абсолютной температуры тела:
4
ST
TR
(2)
где
- постоянная Стефана - Больцмана равная
8
1071,5
42
КмВт
.
Выражение (2) получило название закона Стефана-Больцмана.
17. Законы Вина. Гипотеза Планка и ее применение к тепловому
излучению.
Немецкий физик Вин установил соотношение между
max
,
соответствующей максимальной излучательности
TS
r
абсолютно
черного тела и его температурой:
Tb
max
(3)
где
3
109,2b
Км
. Выражение (3) отражает математически закон
смещения Вина.
Из анализа кривых на рисунке 1 (см. вопр.16) следует, что максимальная
спектральная излучательность
TS
r
пропорциональна
пятой степени температуры:
5
TS
cTr
,
(4)
где
c
- спектральная константа равная
3
103,1
53
КмВт
.
18. Фотоэффект. Законы внешнего фотоэффекта. Формула Эйнштейна.
Фотоэффектом называется электрические явления, которые
происходят при освещении светом вещ-ва, а именно: выход электронов из
вещ-ва (фотоэлектронная эмиссия), возникновение ЭДС.
Вылет электронов из освещенных тел называют внешним
фотоэффектом.
Столетов опытным путем установил следующие законы (внешнего)
фотоэффекта:
1. Число электронов, вырываемых из катода за единицу времени,
пропорционально интенсивности света. (Фототок насыщения
пропорционален энергетической освещенности E).
2. Максимальная начальная скорость фотоэлектронов не зависит от
интенсивности падающего света, а определяется только его частотой.
3. Для каждого фотокатода существует красная граница фотоэффекта, то
есть минимальная частота
0
v
, при которой фотоэффект еще возможен.
Эта частота зависит от химической природы и состояния его поверхности.
Уравнение Эйнштейна для фотоэффекта
Энергия падающего фотона
расходуется на совершение
электроном работы выхода из металла
и на сообщение вылетевшему
фотоэлектрону кинетической энергии:
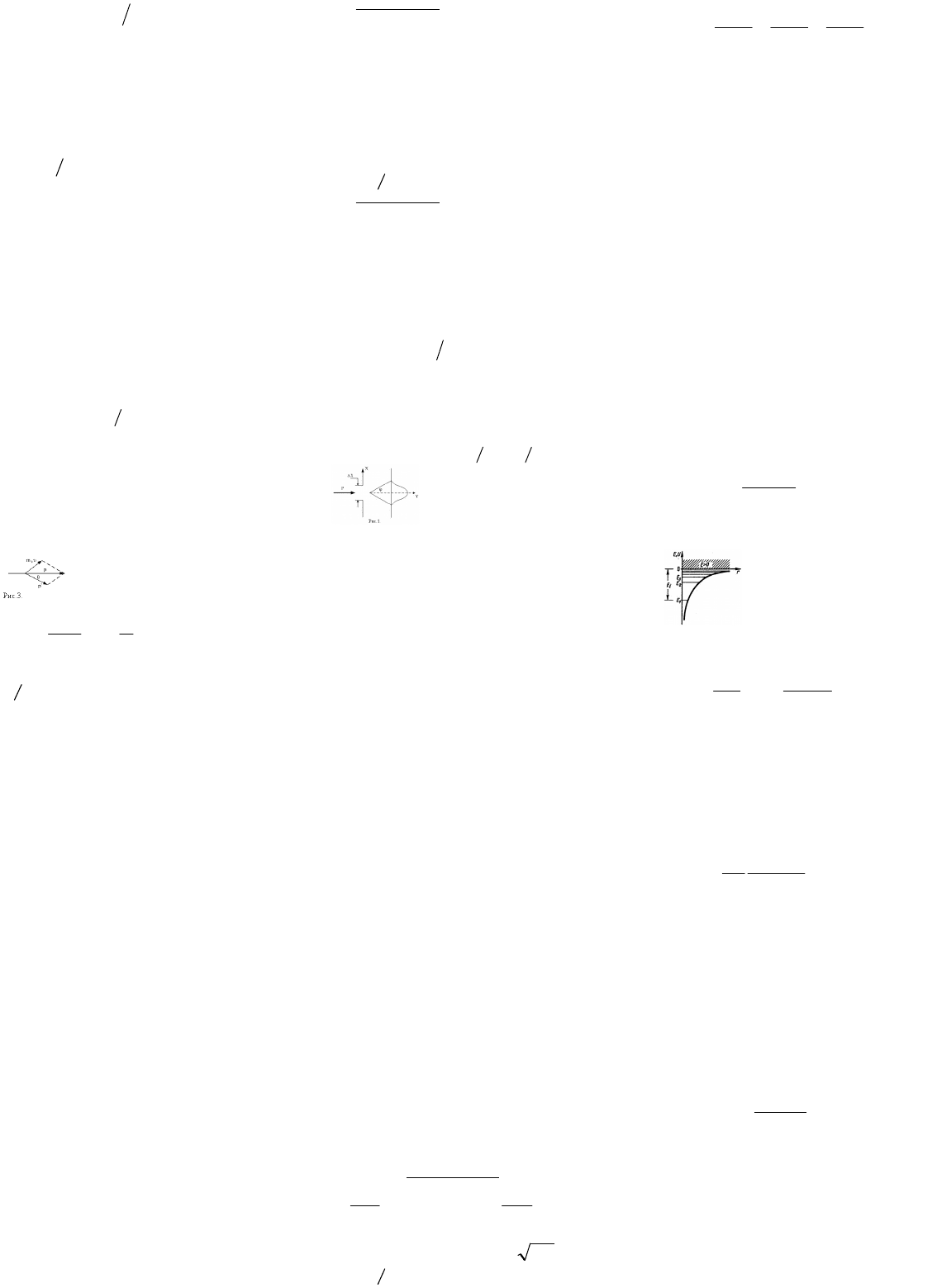
2
2
max
mAhv
(2)
Уравнение (2) называется уравнением Эйнштейна для внешнего
фотоэффекта. Уравнение Эйнштейна позволяет объяснить второй и третий
законы фотоэффекта. Из уравнения (2) непосредственно следует, что
максимальная кинетическая энергия (mV
2
max
/2) возрастает с увеличением
частоты падающего света. С уменьшением частоты кинетическая энергия
(mV
2
max
/2) уменьшается и при некоторой частоте
0
v
она становиться
равной нулю и фотоэффект прекращается (
Ahv
0
).
Отсюда
hAv
0
,
(3)
0
v
- красная граница фотоэффекта (ниже которой фотоэффект не
наблюдается), она зависит лишь от работы выхода электрона из металла (то
есть от химической природы вещества).
19. Эффект Комптона.
Наиболее полно корпускулярные свойства проявляются в эффекте
Комптона. В 1923 году американский физик Комптон исследовал рассеяние
рентгеновских лучей на парафине, атомы которого легкие.
Рассеяние рентгеновских лучей с волновой точки зрения связано
вынужденными колебаниями электронов вещества, так что частота
рассеянного света должна совпадать с частотой падающего света. Однако в
рассеянном свете обнаружилась большая длина волны
.
не зависит от длины волны рассеиваемых
рентгеновских лучей и от материала рассеивающего вещества, но зависит от
направления рассеивания. Пусть
- угол между направлением
первичного пучка и направлением рассеянного света, тогда
2sin2
2
k
, где
Ak 0241,0
(
10
101
A
м).
Этот закон верен для легких атомов (H
2
, C
2
, Br, Al) имеющих электроны,
слабо связанные с ядром. Процесс рассеяния можно объяснить упругим
столкновением фотонов с электронами. Под действием рентгеновских лучей
электроны легко отделяются от атома. Поэтому можно рассматривать
рассеяние свободными электронами. Фотон, имеющий импульс
p
,
сталкивается с покоящимся электроном и отдает ему часть энергии, а сам
приобретает импульс
p
(рис.3).
Используя законы сохранения энергии и
импульса для абсолютно упругого удара, получим
для
выражение:
2
sin
2
2
cm
h
e
, которое совпадает с
экспериментальным, при этом
Acmh
e
02426,0
, что и доказывает
корпускулярную теорию света.
20. Модель атомов. Опыт Резерфорда.
Для объяснения спектров атомов были предложены различные
модели атомов.
В 1903 году английский физик Томсон предложил модель атома,
представляющую собой непрерывно заряженный положительный шар
радиусом
10
10
м, в которую вкраплены электроны. Суммарный
отрицательный заряд, равен положительному заряду шара и поэтому атом
нейтрален.
Однако, в 1911 году английский физик Резерфорд своими опытами по
рассеянию
- частиц опровергает утверждение Томсона о непрерывном
распределении положительного заряда внутри шара. В своем опыте
Резерфорд обнаружил, что при прохождении
- частиц через золотую
фольгу толщиной 1мкм основная их часть испытывает незначительные
отклонения, но некоторые
- частицы (примерно одна из 20000)
отклоняются на углы равные
180
. На основании этих исследований
Резерфорд предложил планетарную модель атома. Согласно этой модели в
центре атома находится положительно заряженное ядро, имеющие размеры
1415
1010
м. Вокруг ядра по орбитам вращаются
электроны. Число электронов равно заряду ядра.
21. Атом водорода по Бору. Постулаты Бора.
Для того, чтобы объяснить линейчатые спектры атомов датский
физик Нильс Бор в 1913 году вводит два постулата.
Первый постулат Бора (постулат стационарных состояний): в атоме
существуют стационарные (не изменяющиеся во времени) состояния, в
которых он не излучает энергию. Энергии этих состояний образуют
дискретный ряд:
1
E
,
2
E
, …,
n
E
. Стационарным
состояниям атома соответствуют орбиты, по которым движутся электроны.
Хотя электроны движутся по стационарным орбитам с ускорением, они не
излучают и не поглощают энергию.
В стационарном состоянии атома электрон, двигаясь по круговой
орбите, должен иметь дискретные значения момента импульса,
удовлетворяющие условию:
nrmL
ne
, n=1, 2, 3,…, где
e
m
- масса
электрона,
- его скорость по n-ой орбите радиуса
n
r
,
2h
.
Второй постулат Бора (правило частот): при переходе электрона с
одной стационарной орбиты на другую излучается (поглощается) квант с
энергией:
kn
EEhv
.
При
nk
EE
происходит излучение фотона (переход из
состояния с большей энергией в состояние с меньшей энергией), при
nk
EE
- поглощение фотона (переход атома в состояние с
большей энергией).
Набор возможных дискретных частот
hEEv
kn
определяет линейчатый спектр атома.
22. Корпускулярно-волновой дуализм вещества. Волны де Бройля.
В 1923 году французский ученый Луи де Бройль выдвинул гипотезу,
что двойственность природы является не только особенностью света, она
универсальна. Частицы вещества на ряду с корпускулярными свойствами
обладают волновыми. Движущейся частице сопоставляется волна. Таким
образом, любой частице, обладающей импульсом, сопоставляют волновой
процесс с длиной волны, определяемой по формуле де Бройля:
mhph
где m
- масса частицы, движущейся со скоростью
.
Волны де Бройля не являются обычными
волнами. Они имеют статистический смысл.
Если через фольгу пропустить
небольшое число электронов, то на экране будет картина, похожая на
мишень, простреленную плохим стрелком. Если число электронов большое,
то получится обычная дифракционная картина. Такое поведение частиц
привело к статистическому толкованию волн де Бройля. Интенсивность
волн де Бройля в каком-либо месте пространства пропорциональна
вероятности обнаружения частицы в этом месте в данный момент.
Поведение отдельных электронов случайно. Повеление большого числа
электронов закономерно. Нельзя угадать движение каждой отдельной
частицы, можно говорить лишь о вероятности ее попадания в данную точку
экрана.
23. Соотношение неопределенностей Гейзенберга.
Каждая частица движется по определенной траектории, то есть в
любой момент времени она имеет определенную координату и импульс.
Микрочастицы из-за наличия у них волновых свойств существенно
отличаются от классических частиц. Нельзя одновременно точно определить
значение координаты и импульса, т. к. нельзя говорить о движении частиц
по определенной траектории. Положение, что микрочастица не имеет
одновременно вполне точные значения координаты и импульса выражено в
соотношение неопределенностей Гейзенберга:
hxP
x
.
Из соотношения неопределенностей следует, что если микрочастица
находится в состоянии с точным значением координаты (
0x
),
то в этом состоянии соответствующая проекция ее импульса оказывается
совершенно неопределенной (
x
P
), и наоборот.
Соотношение неопределенностей Гейзенберга можно пояснить на примере
дифракции электронов. Пусть поток электронов проходит через узкую щель
шириной
x
, расположенную перпендикулярно направлению их
движения (рис. 1).
Дифракционная картина, наблюдаемая на экране, характеризуется главным
максимумом, расположенным симметрично оси
y
, и побочными
максимумами по обе стороны от главного (мы их не рассматриваем, так как
основная доля интенсивности приходится на главный максимум).
До прохождения через щель электроны двигались вдоль оси
y
, поэтому
составляющая импульса
0
x
P
, так что
0
x
P
, а
координата
x
частицы является совершенно неопределенной. В момент
прохождения электронов через щель их положение в направлении оси
x
определяется с точностью до ширины щели, то есть с точностью
x
.
В тот же момент вследствие дифракции электроны отклоняются от
первоначального направления, и будут двигаться в пределах угла
2
.
24. Волновая функция. Уравнение Шредингера.
Квантовая механика способна объяснить поведение микрочастиц.
Подобно тому, как законы Ньютона не выводятся, а является обобщением
большого числа опытных фактов, так и уравнение Шредингера не
выводятся. Оно постулируется. Шредингер записал уравнение, основываясь
на экспериментальных результатах.
Состояние микрочастиц в квантовой механике описывается
волновой функцией
. Она является функцией координат и времени и
может быть найдена из уравнения Шредингера:
t
iU
m
2
2
.
Это временное уравнение Шредингера для случая, когда
c
. Здесь i - мнимая единица (
1i
),
2h
, m - масса частицы,
- оператор Лапласа (
2
2
2
2
2
2
zyx
),
)...( tzyxU
- потенциальная энергия частицы.
25. Атом водорода в квантовой механике.
Самой простой задачей квантовой механики является задача о
движении электрона в кулоновском поле ядра. Это задача об атоме водорода
и водорода подобных ионов: однократно ионизированный гелий и
однократно ионизированный литий.
Потенциальная энергия
взаимодействия электрона с ядром:
r
Ze
rU
0
2
4
,
(1)
где
Ze
- заряд ядра (для атома водорода Z=1), r - расстояние между
электроном и ядром.
Состояние электрон в атоме водорода описывается
волновой функцией
,
удовлетворяющей
стационарному
уравнению Шредингера,
учитывающему выражение (1):
0
4
2
0
2
2
r
Ze
E
m
(2)
где m - масса электрона, а E - полная энергия электрона в атоме.
Уравнение (2) имеет решения,
удовлетворяющие требования
однозначности, конечности и
непрерывности волновой функции
только при следующих собственных
значениях энергии:
2
0
2
42
2
8
1
emZ
n
E
n
, (n=1, 2, 3,…).
(3)
Таким образом, из решения уравнения Шредингера следует, что
энергия электрона в атоме квантуется. Формула (3) дает набор дискретных
значений энергии, совпадающими со значениями энергии, найденными из
спектров. Возможные значения показаны на рис.1. в виде горизонтальных
прямых. Самый низкий уровень энергии
1
E
называется основным, все
остальные – возбужденными. При
0E
движение электрона
является связанным: по мере роста главного квантового числа
энергетические уровни располагаются теснее и при
n
0E
. При
0E
движение электрона является свободным.
Область непрерывного спектра
0E
соответствует
ионизированному атому. Энергия ионизации атома водорода равна:
2
0
2
4
1
8
me
EE
= 13,55 эВ
26. Квантовые числа. Принцип Паули.
Собственные функции
, являющиеся решениями уравнения
Шредингера зависят от трех квантовых чисел: n,
и
m
. n - главное
квантовое число, определяет энергетические уровни электрона в атоме и
принимает значения n = 1, 2, 3,…
- орбитальное квантовое число, оно связано с
квантованием момента импульса
электрона (механического

орбитального момента). То есть
орбитальный момент не может быть
произвольным, а принимает
дискретные значения, определяемые
формулой:
1
L
(1)
При данном значении n
- принимает значения
0,1, 2,…, n-1.
Всего n значений.
m - магнитное квантовое число, связанное с квантованием проекции
момента импульса на выбранное направление (обычно в направлении
магнитного поля по оси z):
mL
z
(2)
Магнитное квантовое число может
принимать следующие значения:
m=0,
1
,
2
,…,
Всего
12
значений.
Принцип Паули - в одном и том же атоме не может быть двух
электронов с одинаковыми квантовыми числами
n
,
,
m
,
S
m
. То есть два электрона должны отличаться по крайней мере
значениями одного квантового числа.
Состояние каждого электрона в атоме характеризуется четырьмя
квантовыми числами:
n
(n = 1, 2, 3,…) – квантует энергию
n
E
,
(
0, 1, 2,…,
1n
) – квантует орбитальный
механический момент
L
,
m
(m = 0,
1
,
2
,…,
) – квантует проекцию
момента импульса на заданное направление
z
z
L
,
S
m
(
21
S
m
) – квантует проекцию спина на
заданное направление
Sz
L
. С возрастанием
n
растет энергия. В
нормальном состоянии атома электроны находятся на самых низких
энергетических уровнях.
27. Строение ядра. Зарядовое и массовое число ядра.
В центре атома сосредоточена основная его масса и весь положительный
заряд. Эта область атома получила название ядра.
Размеры атома
10
10
м, а размеры ядра
1514
1010
м масса ядра составляет 99,95% массы
атома. В нейтральном атоме Z электронов. Заряд ядра положительный и
кратен элементарному заряду
19
106,1
e
Кл. Заряд
ядра можно представить как
Ze
, где Z - зарядовое число, оно
совпадает с химическим номером таблицы Менделеева и равно числу
протонов, входящих в ядро.
Второй важнейшей характеристикой ядра является его масса. Масса ядра
оказалась больше суммы масс протонов, входящих в ядро.
Было сделано предположение, что в состав ядра входят нейтральные
частицы. В 1932 году Чедвиг открыл нейтроны. Иваненко и Гейзенберг
предложили протонно-нейтронную теорию ядра. Ядро расщепляется на
протоны и нейтроны. Они называются нуклонами. Общее число нуклонов в
ядре называется массовым числом A . Общее число нейтронов равно N=A-Z.
Масса покоя протона равна
27
10672,1
p
m
кг,
масса нейтрона равна
27
106749,1
N
m
кг.
Ядро химического элемента обозначают тем же символом, что и
нейтральный атом
X
A
Z
, где Z - атомный номер (заряд ядра), A -
массовое число (число нуклонов в ядре). Ядра с одинаковым зарядовым
числом, но с разным массовым, называются изотопами (изотопы
различаются числом нейтронов). Ядра с одинаковым массовым числом, но с
разным зарядовым, называются изобарами.
28. Свойства ядерных сил.
Особенности ядерных сил:
1. ядерные силы являются силами притяжения
2. ядерные силы короткодействующие (на расстояниях
15
10
м)
3. ядерные силы не зависят от заряда нуклонов
4. ядерные силы зависят от взаимной ориентации спинов
нуклонов (протон и нейтрон образуют дейтрон только при
антипараллельной ориентации спинов)
5. ядерные силы обладают свойством насыщения (каждый
нуклон взаимодействует с ограниченным числом нуклонов)
6. ядерные силы имеют обменный характер (обмен
-
мезонами)
7. ядерные силы не центральные
29. Радиоактивность. Альфа и бетта-распад. Правила смещения.
Радиоактивностью называется превращение неустойчивых изотопов
одного химического элемента в изотопы другого элемента,
сопровождающееся испусканием некоторых частиц. Естественной
радиоактивностью называется радиоактивность, наблюдающаяся у
существующих в природе неустойчивых изотопов. Искусственной
радиоактивностью называется радиоактивность изотопов, полученных в
результате ядерных реакций.
Радиоактивное излучение имеет сложный состав. В магнитном поле
узкий пучок радиоактивного излучения расщепляется на три компонента:
1. слабо отклоняемый пучок положительных частиц (
-
излучение)
2. сильно отклоняемый пучок отрицательных частиц (
-
излучение)
3. не отклоняемый пучок (
-излучение)
-частицы – поток ядер гелия с зарядом Z=2e и массовым числом
A=4 (
He
4
2
). Скорость
-частиц равна
7
10~
м/с.
Попадая в вещество
-частицы активно взаимодействуют с атомами и
молекулами, ионизируют и возбуждают его. Когда энергия
-частицы
уменьшается до теплового движения, она захватывает два электрона и
превращается в атом гелия (He). До этого она проходит путь, называемый
пробегом. Из-за сильного взаимодействия с веществом пробег малый. Лист
бумаги или одежда задерживают
-частицы. Лист алюминия толщиной
0,05 мм также задерживает
-частицы. Ионизирующая способность
-частиц велика и равна
5
10
пар на длине пробега.
-частицы – это поток электронов, вылетающих из ядер со
скоростью
8
10~
м/с. Ядро испускает электрон при превращении
нейтрона в протон:
где
e
0
1
- обозначение электрона,
e
v
~
0
0
- электронное
антинейтрино.
Ионизирующая способность
-частиц в сотни раз меньше, чем у
-частиц, а проникающая способность больше.
-излучение
задерживается слоем алюминия толщиной в 2мм.
Выброс
и
-частиц сопровождается превращением
атомных ядер. Материнским называется ядро испытывающее
радиоактивный распад. Возникающее дочерние ядро оказывается
возбужденным и его переход в основное состояние сопровождается
испусканием
-кванта. При всех превращениях выполняются законы
сохранения заряда, массы и импульса.
Пусть
X
A
Z
- материнское ядро, Y - дочернее ядро, тогда
справедливы правила смещения:
Из этих правил следует, что в результате
- и
-распадов ядра
атомов радиоактивных элементов превращаются в ядра изотопов других
элементов. В ряде случаев дочернее ядро является радиоактивным и
возникает цепочка радиоактивных превращений.
30. Гамма-излучения. Закон ослабление гамма-излучения (Бугера).
-излучение, жесткое электромагнитное излучение (
10
10~
м). Его ионизирующая способность слабая и очень
большая проникающая способность (проходит через слой свинца толщиной
5см).
31. Закон радиоактивного распада.
Число нераспавшихся ядер со временем убывает, а число дочерних –
растет. Самопроизвольный распад атомных ядер подчиняется закону
радиоактивного распада:
где
0
N
- число ядер в начальный момент, N - число ядер в момент
времени t,
- постоянная распада равная доле ядер, распавшихся в
единицу времени.
Средняя продолжительность жизни радиоактивного элемента
выражается формулой:
1
. Период полураспада T
характеризует продолжительность данного распада:
TN
N
exp
2
0
0
или
2exp T
. Отсюда
693,02ln
T
.
Период полураспада колеблется от
7
10
с до
15
10
лет.
32. Дефект масс. Энергия связи.
Экспериментально установлено, что энергия ядра меньше, чем энергия
частиц, из которых оно состоит. Поэтому для расщепления ядра на
составные части нужно затратить энергию. Энергия, которую нужно
затратить для расщепления ядра, называется энергией связи ядра. Mасса
ядра меньше массы составляющих его нуклонов. Но так как всякому
изменению массы должно соответствовать изменение энергии
2
cEm
(c - скорость света), то при образовании ядра
должна выделяться энергия. для расщепления ядра на составные части
необходимо затратить столько же энергии, сколько ее выделяется при его
образовании. энергия связи равна:
ЯNсв
EEE
,
где
N
E
- энергия всех нуклонов,
Я
E
- энергия ядра.
(1)
Следовательно
Эта величина называется дефектом массы ядра. На эту величину
уменьшается масса ядра при образовании его из нуклонов. Часто вместо
энергии связи используют удельную энергию связи. Это энергия связи,
приходящаяся на один нуклон
AEE
св
. Она
характеризует устойчивость атомных ядер. Чем она больше, тем устойчивее
ядро.
33. Деление тяжелых ядер. Цепная реакция деления.
Деления ядер урана при их бомбардировке нейтронами. При этом
образуются латан и барий. Этот процесс положил начало изучения ядерных
реакций нового типа – реакций деления тяжелых ядер под действием
нейтронов. Замечательной особенностью деления тяжелых ядер является то,
что оно сопровождается выделением двух – трех нейтронов, называемых
нейтронами деления. Так как у средних атомов отношение числа протонов и
числу нейтронов равно единице (N/Z=1), а у тяжелых (N/Z=1,6), то
образующиеся осколки перегружены нейтронами и поэтому выделяются
нейтроны деления. Деление ядер сопровождается выделением большого
количества энергии, так как удельная энергия связи ядер средней массы 8,7
МэВ, в то время как у тяжелых 7,6 МэВ.
Цепная реакция деления. Испускаемые при делении ядер вторичные
нейтроны (2,5 штуки на акт деления) могут вызвать новые акты деления, что
делает возможным осуществление цепной реакции. Цепная реакция деления
характеризуется коэффициентом размножения нейтронов К, который равен
отношению числа нейтронов в данном поколении к их числу в предыдущем
поколении
12
NNK
. Необходимым условием развития
цепной реакции деления является
1K
. При меньших K реакция
невозможна. При K=1 реакция идет при постоянном количестве нейтронов
(постоянной мощности выделяемой энергии). Это самоподдерживающая
реакция. При
1K
- затухающая реакция. Коэффициент
размножения зависит от природы делящегося вещества, размеров и формы
активной зоны. Минимальная масса делящегося вещества, необходимая для
осуществления цепной реакции называется критической. Для
U
235
92
критическая масса равна 9 кг, при этом радиус уранового шара равен 4 см.
34. Синтез легких ядер. Термоядерные реакции.
При слиянии ядер выделяется огромная энергия, так как энергия связи
более тяжелых ядер больше, чем в легких. Сливающие ядра несут
положительные заряды, поэтому испытывают огромные силы кулоновского
отталкивания. Энергия такого отталкивания для двух ядер равна:
Такая энергия соответствует температуре
9
106,2 T
К.
При сближении ядер до расстояния
15
10
м начинают действовать
ядерные силы притяжения нуклонов.
Для преодоления кулоновских сил отталкивания энергию относительного
движения ядер увеличивают путем повышения температур. Поэтому
реакции синтеза легких ядер называют термоядерными, потому что
протекают при высоких температурах.
35. Принцип работы и устройство лазеров.
Рубиновый лазер
Один из первых генераторов когерентного света, работающих по схеме трех
уровней с твердым телом в качестве активной, усиливающей среды.
Активным веществом является рубин. Это окись
32
OAl
, в
которой часть атомов Al замещена на Cr. Активным веществом в рубине
являются ионы хрома. От содержания хрома зависит окраска рубина.
Стержень
S
1
S
2
Ксеноновая лампа
1
S
- непрозрачное зеркало,
2
S
-
полупрозрачное зеркало.
Накачка рубина осуществляется ксеноновой лампой, работающей в
импульсном режиме. Эффект усиления света
можно увеличить путем многократного прохождения усиливаемого света
через один и тот же слой усиливающей среды. Для этого торцы рубина
делают зеркальными.
Газовый лазер
Газовые лазеры – это лазеры непрерывного действия. Работают они на 4
уровне системы. Усиливающей средой служит плазма высокочастотного
газового разряда, полученная в смеси гелия с неоном вследствие соударения
с электронами атомы гелия переходят в возбужденное состояние. При
столкновениях возбужденных атомов гелия с атомами неона последние
возбуждаются и переходят на один из верхних уровней неона, близко
расположенных к соответствующему уровню гелия. Переход атомов неона с
этого уровня на один из нижних
2
E
сопровождается с излучением
лазера.
E
1
E
2
E
3
He Ne
Лазерное
излучение
E
36. Взаимные превращения элементарных частиц.
Элементарные частицы – это первичные неразложимые частицы, из
которых, по предположению, состоит вся материя.
Истинно нейтральные частицы не имеют античастиц. Это фотон,
0
-мезон,
-мезон. Они не способны аннигилировать, но
испытывают взаимные превращения.
