Шпоры по Механике грунтов

Подождите немного. Документ загружается.

1.Физические свойства грунтов

Грунты состоят из твердых минеральных частиц («скелет» грунта), воды

и воздуха и, таким образом, представляют собой (при положительной

температуре) трехфазную систему. Все грунты различаются между

собой многими признаками. Для механики грунтов наиболее важными

являются их физические и механические свойства. Количественные

показатели свойств грунтов называют характеристиками. Основные из

этих характеристик определяют опытным путем в лаборатории или в

полевых условиях, остальные вычисляют затем по найденным основным

характеристикам. Основными характеристиками физических свойств

грунтов служат: гранулометрический состав, удельный вес грунта

природного сложения, удельный вес частиц грунта, влажность, границы

раскатывания и текучести.

Гранулометрический состав характеризует содержание по массе групп

частиц (фракций) грунта различной крупности по отношению к общей

массе абсолютно сухого грунта. В зависимости от содержания в грунте

частиц разных размеров определяют степень неоднородности

гранулометрического состава.Степень неоднородности

гранулометрического состава не может быть меньше единицы и

практически не бывает больше 200.

Удельным весом грунта природного сложения у называют отношение

массы грунта, включая массу воды в его порах, к занимаемому этим

грунтом объему, включая поры, умноженное на ускорение свободного

падения g, равное 9,81 м/с2. Удельные веса нескальных грунтов

природного сложения, встречающихся в строительной практике, имеют

значения от 15 до 22 кН/м3.Разные грунты имеют удельные веса частиц,

мало отличающиеся между собой. Удельные веса частиц песков

составляют от 26,5 до 26,8 кН/м3, супесей и суглинков — от 26,0 до 27,0

кН/м3 и глин — от 26,0 до 27,5 кН/м3.

Пластичность?? и?? консистенция?? глинистых?? грунтов.

Изменение влажности оказывает большое влияние на свойства

глинистых грунтов, которые при этом могут переходить из твердого

состояния в полутвердое, затем в?пластичное?и,?наконец,?в?текучее или

наоборот. Если образцу маловлажного глинистого грунта попытаться

путем раскатывания придать форму проволоки, то он будет крошиться

Основными физико-механическими свойствами

грунтов являются:

1. Гранулометрический состав, т. е. процентное содержание по весу

частиц различной крупности: гальки (40 мм), гравия (2—40 мм), песка

(0,25—2 мм), песчаной пыли (0,05— 0,25 мм), пылеватых частиц (0,005

—0,05 мм) и глинистых частиц (менее 0,005 мм).

2. Объемный вес, т. е. отношение веса грунта к его объему при

естественной влажности. Для грунтов он составляет от 15 до 20 кн/м3

(1,5—2 г/,и3).

3. Пористост ь — объем пор, заполненных водой и воздухом в

процентах от общего объема грунта. Она характеризуется

коэффициентом пористости, представляющим собой отношение объема

занятых водой и воздухом пор к объему твердых частиц.

4. Весовая влажность — отношение веса воды к весу сухого грунта в

5. Связность (взаимное сцепление частиц) — способность грунта

сопротивляться разделению на отдельные частицы под действием

внешних нагрузок. Типичным представителем связных грунтов являются

глину, несвязных грунтов — сухие пески.

6. Пластичность — свойство грунта изменять свою форму под

действием внешних сил и сохранять эту форму после удаления внешних

сил. Наибольшей пластичностью отличаются влажные глины; песок и

промытый гравий — материалы непластичные.

7. Прочность. В связи с тем, что грунты, особенно не связные, имеют

незначительную прочность, не удается пользойваться такими

характеристиками, как прочность на одноосное.

8. Сопротивление сдвигу. Под действием механической нагрузки грунт

разрушается в результате деформаций, превосходящих предельные

значения. Считается, что эти деформации происходят по плоскостям

скольжения (плоскостям, по которым происходит сдвиг одних частиц

относительно других). При разрушении грунта частицы сопротивляются

относитель—ному сдвигу. Это сопротивление характеризуется

величиной, сцепления. Сопротивление сдвигу по плоскости скольжения

уве-личивается в результате внутреннего трения частиц, возникаю щего

под действием нормальных напряжений.

Если выделить условно сдвигаемую частицу грунта, то напряжения,

действующие в плоскости скольжения частицы, могут быть упрощенно

представлены так, как показано на рис. 49.

Рис. 48. Предел прочности на одноосное сжатие мерзлых грунтов в

зависимости от температуры и влажности ш в :

Рис. 49. Условия равновесия частицы грунта на откосе

9. Угол естественного откоса ф — угол у основания конуса, который

образуется при отсыпании разрыхленного грунта с некоторой высоты.

Этот угол зависит от величины коэффициента внутреннего трения и от

связности. Для несвязных грунтов угол естественного откоса равен углу

внутреннего трения. Величины углов естественного откоса приводятся в

табл. 8.

10. Сопротивл ени е грунта вдавливанию. При вдавливании в грунт

штампа или какой-либо опорной поверхности (ходовой части машины,

элемента рабочего органа) под штампом происходят деформации в

условиях, близких к всестороннему сжатию (т. е. когда на элемент

грунта действуют одновременно окружающий массив и поверхность

штампа так, что элемент оказывается сжатым со всех сторон).

Чем ближе к поверхности грунта расположен элемент, тем меньше

влияние всестороннего сжатия. Вдавливание на небольшую глубину (до

1 см) называют смятием. При этом усилие, необходимое для

вдавливания штампа, во много раз меньше, чем при вдавливании

штампа на значительную глубину.

В частности, допускаемые нагрузки для ходовых частей” машин

предусматривают погружение до 6—12 см. Величина усилия,

необходимого для вдавливания штампа, зависит от размеров

штампа. Чем меньше он, тем больше должно быть удельное усилие

при вдавливании.

11. Абразивность (от латинского слова abrasio — соскабливать) —

способность материала оказывать истирающее действие на другой

материал. Абразивность грунтов из горных пород в значительной

степени определяет износ рабочих органов землеройных машин.

Имеются различные методы оценки аб-разивности, однако все они

пока еще являются относительными, так как износ зависит от

удельных давлений, скорости взаимного перемещения и

прочностных показателей. При одних и тех же прочностных

показателях величина износа может быть различной.

Коэффициент трения грунта о сталь зависит от состояния

поверхности стали и физико-механических свойств грунта.

12. Разрыхляемость определяется как отношение объема

разрыхленного грунта Vp к объему V первоначальному (в плотном

теле).

Первоначальное разрыхление — это разрыхление, наблюдаемое

сразу после отделения грунта от массива; остаточное разрыхление

наблюдается через некоторое время после укладки грунта в отвал

или насыпь, где происходит его самоуплотнение без трамбования.

Копание и резание грунтов

Копание — совокупность процессов отделения грунта от массива,

включающих резание грунта, перемещение его по рабочему органу

и впереди последнего, а в отдельных случаях и перемещение внутри

рабочего органа (в частности, в ковшах экскаваторов).

Резание — процесс отделения грунта от массива при помощи

режущей части рабочего органа, обычно имеющей вид клина.

Одно из них — движение, при котором отделяется стружка1, другое

(оно может быть названо движением подачи) — при котором

изменяется толщина стружки.

Скорость движения подачи обычно в несколько раз меньше

скорости главного движения. Соотношение скоростей этих

движений в известной мере определяет траекторию рабочего органа.

Рис. 50. Геометрия рабочего органа

В землеройно-транспортных машинах режущий орган (нож)

предварительно внедряется в грунт до определенной глубины, а

затем, двигаясь в нужном направлении, срезает стружку заданной

толщины.

Как правило, внедрение в грунт происходит в результате

одновременного перемещения ножа вглубь и вперед.

Механику отделения грунта от массива в процессе резания можно

представить так.

Термином «стружка» пользуются при обработке металлов, он не

всегда отражает физическую сущность процессов, происходящих

при резании грунтов, однако удобен при расчетах сил

сопротивления грунта резанию и копанию, наполнения ковша и

производительности землеройных машин. Поэтому применяется

условно.

Указанный способ моделирования процесса резания был впервые

предложен М. И. Гальпериным и В. Д. Абезгаузом.

У передней грани формируется уплотненное ядро (рис. 52), которое,

двигаясь перед режущей частью рабочего органа, внедряется в

массив и отделяет стружку. Размеры ядра в процессе резания

непрерывно изменяются, а само ядро периодически обновляется.

При углах резания, меньших 30°, у большинства грунтов ядро не

образуется. В этом случае стружка отделяется под воздействием

передней грани рабочего органа.

Рис. 51. Внедрение штампа у одной открытой стенки

Грунт отделяется от массива в результате сдвига или отрыва.

Характер этого отделения зависит от физико-механических свойств

грунта, геометрии рабочего органа и режимов работы.

Определение отдельных параметров процесса резания и копания

грунта, усилий, наивыгоднейших режимов, геометрии рабочего

органа из-за сложности процесса и одновременного влияния многих

факторов пока еще не получило аналитического решения. В

основном усилия и режимы подбираются на основе

экспериментальных данных.

Рис. 53. Удельное сопротивление резанию при разработке

До определенных значений с по мере его увеличения второй фактор

оказывает большее влияние и, следовательно, величина kp

уменьшается. После увеличения с сверх определенных значений

большее влияние оказывает всестороннее сжатие и сопротивление

kp увеличивается. Это продолжается, пока значение с не достигнет

величины си после чего значения kp стабилизируются.

С увеличением Ь величина kv уменьшается и после определенных

значений Ь она также стабилизируется.

При полусвободном и свободном резании удельное сопротивление с

увеличением с при постоянном b уменьшается и после

определенных значений с тоже стабилизируется.

Величина kp в значительной степени зависит от физико-

механических свойств грунта и в большей степени от его прочности

на одноосное сжатие. Последняя зависит от влажности, объемного

веса, пластичности, связности грунта и других параметров. Так как

прочность на одноосное сжатие многих талых грунтов мала и

трудно поддается измерению, а для некоторых грунтов, например

для песков, ее вообще нельзя измерить, то трудность разработки

характеризуют категорией грунта.

Рис. 54. Ударник конструкции ДорНИИ

Под действием удара стержень внедряется в грунт. В

зависимости от физико-механических свойств грунта для

внедрения стержня на глубину 0,1 м требуется различное число

ударов: например, в просеянный песок влажностью 9,2 требуется

всего один удар, а в легкий суглинок вл а леностью 10,6% — 12

ударов. Величина kp зависит также от геометрии режущей части

рабочего органа. Опыты показывают, что для большинства

грунтов оптимальное значение угла резания б должно быть 20—

30°. При меньших углах б лезвие получается очень тонким. С

увеличением этого угла удельное сопротивление резанию

возрастает. Задний угол а должен быть не меньше 7°, особенно

для экскаваторов и бурильных машин, при работе которых в

результате сложного перемещения рабочего органа угол а

фактически уменьшается. При а = 7-М0° не всегда можно

достигнуть, чтобы угол резания составлял 20—30°, так как в этом

случае угол заострения р не превышает 25°, а при такой величине

угла заострения прочность режущей части рабочего органа

недостаточна. Поэтому угол р делают больше 25°, тогда при а —

7—10° угол резания получается очень часто больше 20—30°.

С увеличением угла б на каждые 10° удельное сопротивление

резанию возрастает примерно на 10—12%. Поэтому, если

прочность режущей части достаточна, то следует работать на

углах, близких к оптимальным значениям.

2. Сила сопротивления внедрению режущего лезвия рабочего

органа в грунт Р п (в направлении, нормальном к траектории) , т.

е. сила подачи.

Как правило, режущая часть рабочего органа быстро затупляется

и на ней образуется так называемая площадка затупления.

Профиле площадки затупления может совпадать или не

совпадать с траекторией движения режущего лезвия. На форму

профиля влияют физико-механические свойства грунта и режимы

работы.

Рис. 55. Виды затупления режущего лезвия

На рис. 55 показан различный характер затупления режущего

лезвия и возникающие при этом силы.

Если траектория движения совпадает с профилем площадки

затупления и радиус закругления незначителен, то можно

считать, что сопротивление Рп возникает только при отжиме

рабочего органа от поверхности грунта (рис. 55.а) в результате

упругого последействия.

Если траектория движения совпадает с профилем площадки

затупления и при этом на режущей кромке образовался радиус

закругления, определяющий площадку затупления, то

появляются дополнительные силы, отжимающие рабочий орган в

процессе резания.

Если профиль траектории не совпадает с профилем площадки

затупления, то выступающая за траекторию часть (рис. 55, в)

внедряется в грунт. Сила Р„ при этом определяется

сопротивлением внедрению выступающей части в грунт.

Рис. 56. Изменение усилий при вдавливании плоского штампа в

мерзлый песок в условиях всестороннего сжатия

Классификационные показатели грунтов.

Основные физические показатели, характеризующие состав и

состояние грунтов. Гранулометрический состав, плотность

грунтов, удельный вес, влажность, пористость. Пластичность

глинистых грунтов, границы текучести и раскатывания,

показатели текучести. Методы определения физических

характерист

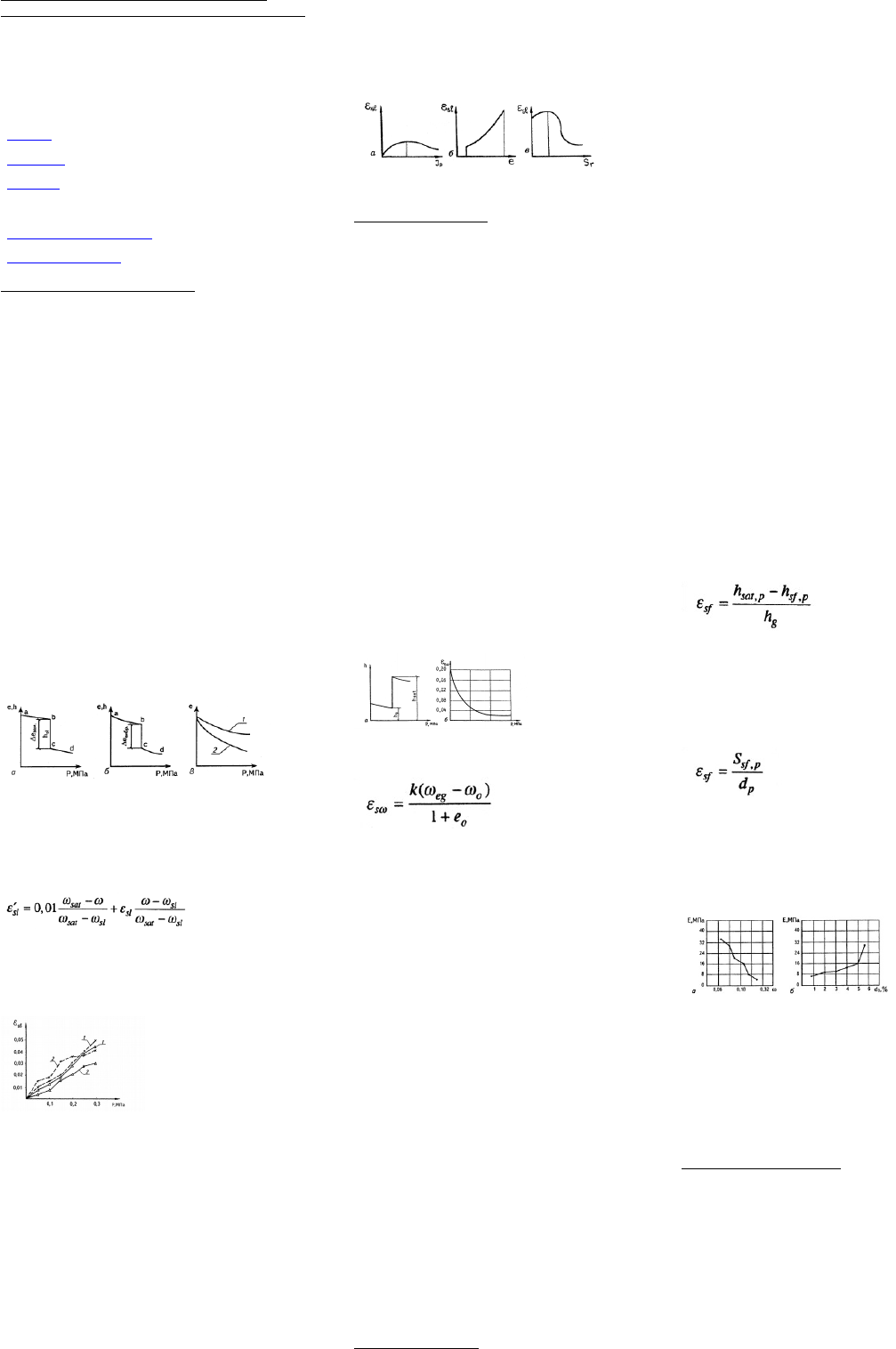
2. Структурно-неустойчивые грунты, их

особенности как основания для строительства.

Структурно-неустойчивыми называют такие грунты, которые обладают

способностью изменять свои структурные свойства под влиянием

внешних воздействий с развитием значительных осадок, протекающих,

как правило, с большой скоростью. К основным воздействиям относятся

увлажнение грунтов, промерзание и оттаивание, суффозия и

выветривание, внешние нагрузки, перемятие грунтов и др.

Такое название они получили потому, что при определенных условиях

их природная структура сравнительно резко нарушается. К структурно-

неустойчивым относятся следующие грунты:

- лессовые, структура которых нарушается при замачивании их под

нагрузкой;

- набухающие, которые при увлажнении способны существенно

увеличиваться в объеме даже под нагрузкой;

- засоленные, песчано-глинистые отложения, в которых накопление

солей произошло в процессе их формирования

сильносжимаемые грунты, деформационные и прочностные свойства

которых резко изменяются при нарушении их природной структуры;

- торфы и заторфованные грунты, обладающие очень большой

сжимаемостью и малой прочностью;

- мерзлые и вечномерзлые, структура которых нарушается при

оттаивании.

Лессовые просадочные грунты широко распространены в

Среднем и Нижнем Поволжье, Западной Сибири, на Северном Кавказе и

в других районах страны.

В зависимости от увлажнения лессы различным образом ведут себя под

действием внешней нагрузки. Так, в «сухом» состоянии (ω≤0,09) лессы

отличаются значительной прочностью и относительно высокой несущей

способностью. В таком состоянии они выдерживают давление на грунт

Р≤0,4МПа при небольших осадках и способны сохранять достаточно

большую высоту вертикального откоса.

Просадочные грунты характеризуются:

относительной просадочностью εsl — относительным сжатием грунтов

при заданном давлении после их замачивания (см. п. 4.10);

начальным просадочным давлением Psl — минимальным давлением, при

котором проявляются просадочные свойства грунтов при их полном

водонасыщении;

начальной просадочной влажностью ωsl — минимальной влажностью,

при которой проявляются просадочные свойства грунтов.

Относительная просадочность грунта определяется в компрессионных

приборах по методу одной или двух кривых (ГОСТ 23161—78).

По методу одной кривой (рис. 5.18,а,б) испытывают пробу грунта

естественной влажности при заданном давлении. После стабилизации

осадки грунт насыщают водой, замеряя просадку, и испытание

продолжают уже для водонасыщенного грунта.

По методу двух кривых (см. рис. 5.18,в) компрессионным испытаниям

подвергают две пробы грунта: одну — при естественной влажности,

вторую — при полном водонасыщении, после чего строят графики

зависимости е, ∆h=ƒ(P). На кривых (см. рис. 5.18,а) различают три

области деформирования просадочных грунтов: область ab,

соответствующую сжатию грунта в ненарушенном состоянии; область

bc, характеризующую просадку грунтов, и область cd — уплотнение

грунта с ненарушенными структурными связями. По кривым e, Δh=ƒ(P)

просадочных грунтов непосредственно определяют значение изменения

коэффициента пористости грунта при просадке ∆εsl а также

относительную просадочность εsl,по формуле (4.5).

Рис. 5.18. Компрессионные кривые просадочного грунта: а, б — по

методу одной кривой, соответственно, пылевато-глинистых при

замачивании и рыхлых песчаных при вибрации; в — по методу двух

кривых; 1 — для грунта естественной влажности; 2 — для грунта,

насыщенного водой

Согласно СНиП 2.02.01—83* расчетным состоянием просадочных

грунтов по влажности является полное водонасыщение Sr> 0,8.

Относительная просадочность грунта при его неполном водонасыщении

(ωsl≤ω≤ωsat) определяется по формуле

??????????????????????(5.34)

где εsl — относительная просадочность при полном водонасыщении

Начальное просадочное давление Psl — это давление, при котором

относительная просадочность esl = 0,01, т.е. при котором грунт

считается просадочным. Если провести серию компрессионных

испытаний лессового грунта с замачиванием образцов при различных

нагрузках, то нетрудно получить график зависимости относительной

просадочности от давления (рис. 5.19).

Рис. 5.19. Зависимость относительной просадочности от нормального

давления лессового суглинка Георгиевска (1) и Ростова-на-Дону (2) (по

Я.Д. Гильману, 1991):?Δ — метод одной кривой; х — метод двух кривых

За начальную просадочную влажность ωsl по аналогии принимается

влажность, при которой в условиях заданных давлений esl = 0,01.

Ее значения зависят от напряженного состояния грунта, природной

плотности и прочности структурных связей. С увеличением давления на

грунт начальная просадочная влажность уменьшается.

Значения модуля общей деформации лессового грунта изменяются в

широком интервале. Это обусловлено тем, что они существенно зависят

от исходной влажности и пористости грунта. В качестве примера в табл.

5.6 приведены систематизированные значения модуля деформации

лессовых суглинков Ростовской области. Данными табл. 5.6 можно

воспользоваться в том случае, когда отсутствуют результаты штамповых

испытаний грунта с учетом прогнозируемой его влажности.

Таблица 5.6. Значения модуля деформации лессовидных суглинков в

диапазоне нормативных давлений 0,1—0,3 МПа (по Я.Д. Гильману,

1991)

Степень

влажности Sr

Модуль деформации Е, МПа , при коэффициенте

пористости е, равном

0,56-0,65 0,66-0,75 0,76-0,85 0,86-0,95 0,96-1,05

0,3 50 44 38 30 22

0,4 35 30 25 20 14

0,5 25 21 17 13 8

0,6 18 15 12 9 6

0,7 14 12 9 7 5

0,8 12 10 7 6 4

0,9 10 8 6 5 3

1,0 8 7 5 4 2

Просадка как деформация зависит (рис. 5.20) от минералогического

и гранулометрического составов грунта, его влажности, плотности и

напряженного состояния, поэтому для каждого лессового грунта

определяют просадочность при давлениях, которые он будет

испытывать в основании под сооружением.

Рис. 5.20. График зависимости относительной просадочности от Ip,

е и Sr: а — от числа пластичности; б — от коэффициента

пористости; в — от степени влажности

Набухающие грунты имеют широкое распространение.

Такие грунты распространены в Египте, Бирме, США, ЮАР, а в

Индии более 30% территории занимают так называемые хлопковые

почвы. В странах СНГ такие группы встречаются в Казахстане,

Грузии, Азербайджане, Украине, России (Поволжье, Северный

Кавказ и других районах).

Характерной особенностью набухающих грунтов является резкое

снижение их несущей способности при замачивании.

Набухающие глинистые грунты характеризуются следующими

параметрами:

давлением набухания Psω;

влажностью набухания ωsω;

относительным набуханием при заданном давлении εsω;

относительной усадкой при высыхании εsh.

Эти характеристики определяются в лабораторных условиях

согласно ГОСТ 24143-80.

Давлением набухания Psω грунта называют то минимальное

давление, при котором грунт не набухает.

Давление набухания развивается в глинистом грунте как реакция

внешней нагрузке, передаваемой на грунт от сооружения или

выщелачивающей толщи грунта. Это давление может достичь 0,8

МПа и возникает в основании гидротехнических сооружений после

пуска в них воды, что приводит к деформациям этих сооружений,

вследствие неравномерного поднятия фундамента на разных

участках.

За влажность набухания ωsω принимается влажность, полученная

после завершения набухания образца, обжатого без возможности

бокового расширения заданным давлением Р. С увеличением

плотности грунта влажность набухания уменьшается.

Набухаемость грунтов оценивают коэффициентом относительного

набухания εsω, который находят испытанием грунта в одометре, и

нагружают давлением, которое ожидается на данной глубине с

учетом давления от возводимого сооружения. Затем в одометр

подают воду. В результате чего происходит набухание образца

грунта, т.е. поршень одометра будет перемещаться вверх. По

данным испытания можно построить кривую (рис. 5.21,а).

Рис. 5.21. Зависимости деформаций набухающего грунта (а) и

относительного набухания (б) от нормального давления

При экранировании поверхности и изменении водно-теплового

режима относительное набухание находят по формуле

?????? (5.35)

где k — коэффициент, определяемый опытным путем, а при

отсутствии экспериментальных данных принимается равным 2;

ωeg — конечная (установившаяся) влажность грунта;

ω0 — начальная влажность грунта;

ε0 — начальное значение коэффициента пористости грунта.

Значения относительного набухания зависят от плотности и

начальной влажности грунта. С увеличением начальной влажности

образца грунта набухание снижается тем быстрее, чем больше ωо.

Снижение прочностных характеристик при набухании происходит у

всех набухающих грунтов. После набухания грунта модуль

деформации уменьшается в несколько раз, что наглядно видно из

табл. 5.7. Также видно, что модуль деформации набухающих глин,

определенный в лабораторных условиях, значительно ниже, чем

определенный при полевых испытаниях.

Таблица 5.7. Значения модуля деформации набухающих глин до и

после замачивания (по Е.А. Сорочану, 1989)

Глины

Значения модуля

деформации, МПа

Отношение значений

модуля деформации,

определенного

полевым методом,

к лабораторным Eлаб

/ Епол

Лабораторные

Елаб

Полевые

Епол

Сарматские

(Керчь):

?? до замачивания

?? после

замачивания

11,0

3,0

25-30

9-10

2,3-2,7

3,0-3,3

Киммерийские

(Керчь):

?? до замачивания

?? после

замачивания

8,0

2,7

7-11

2,6

2,6-4,1

Хвалынские

(Волгоград)

?? до замачивания

?? после

замачивания

8,0

2,0

16-20

3,6

2,0-2,5

1,8

Так, для глины природной влажности модуль деформации по

полевым данным больше, чем по лабораторным, в 2,3—2,7 раза, а

для увлажненной — в 3,0—3,3 раза.

Засоленные грунты широко распросфанены в

Прикаспийской низменности, Центральном Поволжье, Западной и

Восточной Сибири. К засоленным грунтам относятся песчано-

глинистые отложения, в которых накопление солей произошло в

процессе их формирования. При оценке грунтов важно знать

содержание в них водорастворимых солей.

В соответствии с классификацией В.П. Петрухина (1989) к

засоленным относятся грунты, минимальное содержание в

которых водорастворимых (легко- и среднерастворимых) солей

от массы абсолютно сухого грунта, составляет:

Крупнообломочные с содержанием песчаного

заполнителя < 40% или глинистого < 30%

То же, но при содержании песчаного заполнителя >

40%

0,5%

Песчаные

0,5% и

более

Супеси и суглинки

5% и

более

Глины 10%

При замачивании засоленных грунтов наблюдаются:

появление суффозионной осадки при длительной фильтраци;

набухание или просадка грунта;

снижение прочностных характеристик грунта;

повышение агрессивности подземных вод.

К легкорастворимым солям относятся: хлориды — NCI, СаСl2;

сульфаты — Na2SO4 и карбонаты натрия — NaHCO3 и Na2CO3;

к среднерастворимым — гипс CaSO4 · 2H2O и ангидрид CaSO4.

Карбонаты растворяются трудно и медленно, поэтому особого

влияния на свойства грунтов не оказывают, однако они могут

способствовать созданию горизонтов агрессивных вод, которые

разрушительно влияют на подземные конструкции зданий и

сооружений.

Причинами, приводящими к засолению грунтов, являются:

бессточный рельеф;

недостаточное увлажнение в результате преобладания испарения

над осадками;

наличие в грунтах или грунтовых водах повышенного количества

солей;

малая проницаемость грунтов или наличие водоупорных

прослоек;

?несовершенство систем орошения;

техногенное воздействие на гидросферу застроенных или

застраиваемых территорий;

фильтрация через грунты растворов химических веществ

производственных отходов из накопителей, шламонакопителей,

отвалов.

Засоленные глинистые грунты характеризуются относительным

суффозионным сжатием εsƒ и начальным давлением

суффозионного сжатия Psƒ.

Величина относительного суффозионного сжатия должна

определяться, как правило, по данным испытаний засоленных

фунтов с длительным замачиванием.

Значение εsƒ при компрессионно-фильтрационных испытаниях

определяется по формуле

?? ?(5.36)

где hsat,p — высота образца после замачивания его до полного

водонасыще-ния при некотором давлении Р;

hsƒ,p — высота того же образца после длительной фильтрации

воды и выщелачивания солей при давлении Р;

hg — высота образца природной влажности при давлении от

собственного веса.фунта на рассматриваемой глубине σzg.

При полевых испытаниях засоленных грунтов статической

нагрузкой с длительным замачиванием значение? εsƒ

определяется по формуле

???? ?(5.37)

где Ssƒ,p — суффозионная осадка штампа при давлении Р;

dp — зона суффозионной осадки.

За начальное давление суффозионного сжатия Рsƒ принимается

давление, При котором εsƒ= 0,01.

Маловлажные и сухие грунты при увлажнении резко изменяют

свои деформационные, прочностные и фильтрационные свойства

из-за выноса солей. В качестве примера на рис. 5.22 показано

влияние изменения влажности засоленных грунтов и

выщелачивания солей на модуль деформации.

Рис. 5.22. Зависимость модуля общей деформации засоленных

глинистых грунтов от влажности (а) и выщелачивания солей (б)

Как видно из рис. 5.22, рассматриваемые грунты при

естественной влажности (ω = 0,08) и природном содержании

солей (d0 = 5,7%) имеют высокий модуль деформации. При

увеличении влажности (см. рис. 5.22,а) или выщелачивании солей

(см. рис. 5.22,6) снижение модуля деформации составляет 4—10

раз и более (по СБ. Ухову и др., 1994).

Выщелачивание водорастворимых соединений приводит к

уменьшению плотности и устойчивости грунтов, а также к

увеличению их водопроницаемости. Фильтрующая через грунт

вода становится агрессивной по отношению к бетону, раствору и

металлу.

Торфы и заторфованные грунты представляют собой

грунты органогенного происхождения, образовавшиеся в болотах

в результате накопления и разложения растительных остатков в

условиях затрудненного доступа воздуха.

Специфическими особенностями заторфованных грунтов

являются во-донасыщенность, большая сжимаемость, медленное

протекание осадок во времени, анизотропия и изменчивость

характеристик под нагрузкой.

К заторфованным относятся песчаные и глинистые грунты,

содержащие в своем составе 10—50% (по массе) органических

веществ. При содержании органических веществ 50% и более

грунт называется торфом.

Поскольку биогенные слабые грунты (сапропели, заторфованные

и торфяные) содержат значительное количество органического

вещества J, % (или? Jот, долях единицы), то их разделяют по этой

составляющей (рис. 5.23). Как видно из рис. 5.23, влияние

содержания органических веществ в грунте на изменение

влажности существенно для нормальнозольных торфов.

Рис 5.23. Зависимость природной влажности от содержания

органических веществ в слабых грунтах (по Л.С. Амаряну, 1990)

Так как сапропели (пресноводный ил) по содержанию органических

веществ захватывают области как торфяных (J ≥ 50%), так и

заторфованных грунтов (J< 50%), то их подразделяют на минеральный

— 10 < J≤30%, среднеминеральный — 30 < J≤50% и слабоминеральный

— J > 50%. Сапропели, как правило, имеют коэффициент пористости

более 3, а показатель текучести более 1.

Различие в структуре и дисперсности твердой фазы слабых грунтов не

позволяет по величине J оценить однозначно изменчивость их

прочностных показателей.

На рис. 5.24 показаны изменения предельного сопротивления сдвигу т,

определенные крыльчаткой в полевых условиях, в зависимости от J (по

Л.С. Амаряну, 1990). Как видно из рис. 5.24, при одинаковых значениях

прочность сапропелей и торфов по величине тотличается в 4—5 раз.

Данные рис. 5.24 позволяют установить классификационные отличия

между торфяными, заторфованными грунтами и сапропелями.

Рис. 5.24. Зависимость сопротивления сдвигу слабых

органоминеральных фунтов от содержания органических веществ

Эти грунты имеют низкую прочность. Так, у сапропелей угол

внутреннего трения φ близок к нулю, а удельное сцепление С в

зависимости от степени уплотненности и минерализации находится в

пределах 0—20 кПа. У погребенных торфов в зависимости от степени

разложения эти характеристики составляют: φ = 10-22°; С = 10—30 кПа

(по СБ. Ухову и др., 1994).

Мерзлые и вечномерзлые грунты в зависимости от их

температуры и длительности ее действия делят на немерзлые (талые),

мерзлые и вечно-мерзлые.

Мерзлыми называются грунты с отрицательной температурой, в которых

часть поровой воды находится в замерзшем состоянии (в виде

кристаллов льда). Мерзлые грунты являются четырехкомпонентными

системами, в которых кроме твердой, жидкой и газообразной фаз

существует лед.

Если неминерализованная вода замерзает при 0 °С, то грунт при такой

температуре замерзает только при наличии в них свободной

неминерализованной воды, поскольку связанная вода в виде тонких

пленок и минерализованная вода замерзает при более низкой

температуре.

Вечномерзлыми называют грунты, находящиеся в мерзлом состоянии в

течение трех лет и более. Вечномерзлые грунты представляют собой

ярко выраженные структурно-неустойчивые грунты, так как при их

оттаивании происходят просадки в результате нарушения природной

структуры.

При промерзании оттаявшего грунта возможно его пучение.

Поверхностный слой грунта, промерзающий зимой и оттаивающий

летом, называют деятельным слоем, или слоем сезонного промерзания и

оттаивания, поскольку в нем происходят интенсивные процессы,

связанные с промерзанием и оттаиванием грунта.

Если наблюдать за образцом глинистого грунта (по Б.И. Далматову,

1988), помещенного в морозильную камеру, то при изменении

температуры полученная кривая будет иметь четыре участка (рис. 5.25).

Первый участок аb соответствует понижению температуры с

переохлаждением поровой воды. Второй участок bc характеризует

резкое повышение температуры грунта, что связано с кристаллизацией

части воды в образце грунта до значения Тbƒ, соответствующего началу

замерзания. Третий участок cd, параллельный оси времени t,

характеризует резкий переход большей части воды в лед. На четвертом

участке de происходит постепенное понижение температуры уже

замерзшего фунта, т.е в этот период замерзает вода, не замерзшая при

значении Тbƒ.

В зависимости от вещественного состава и температурно-влажностны

условий мерзлые фунты делятся на твердомерзлые, пластичномерзлые и

сыпучемерзлые.

Рис. 5.25. График процесса замерзания фунта во времени (по Б.И.

Далматову, 1988)

К твердомерзлым относят грунты, характеризуемые относительно

хрупким разрушением и практической несжимаемостью под нагрузкой.

Под действием нагрузок от сооружений такие фунты практически не

сжимаются (модуль деформации Е > 100 МПа), так как сцементированы

льдом.

К твердомерзлым относятся крупнообломочные грунты с суммарной

влажностью ωtot > 0,03, а также песчаные и глинистые, если их

температура ниже значений, приведенных в табл. 5.8, при которых грунт

переходит из пластичного в твердомерзлое состояние.

Таблица 5.8. Температура перехода грунта из пластичного в

твердомерзлое состояние

Наименование грунта

Температура,

T°С

Крупнообломочный 0

Песок:

?? крупный и средней крупности

?? мелкий и нылеватый

0,1

0,3

Супесь 0,6

Суглинок 1,0

Глина 1,5

Пластичномерзлыми являются грунты, сцементированные льдом, но

имеющие вязкие свойства и характеризуемые сжимаемостью под

нагрузкой. К ним относятся песчаные и пылевато-глинистые грунты

с температурой, вышеуказанной в табл. 5.8. Они характеризуются

достаточной сжимаемостью (Е < 100 МПа) и вязкими свойствами.

Сыпучемерзлые — это крупнообломочные, гравелистые и песчаные

грунты, имеющие отрицательную температуру, но не

сцементированные льдом вследствие малой их влажности.

Суммарная влажность таких грунтов ωtot≤ 0,03. Их свойства

практически не изменяются под влиянием температуры и близки к

свойствам тех же грунтов в немерзлом состоянии.

В связи с тем, что мерзлые грунты состоят из твердой минеральной

части, пор, льда и незамерзающей воды, то дополнительно к

характеристикам талых грунтов для мерзлых определяются:

суммарная влажность мерзлого грунта ωtot, которая слагается из

влажности, обусловленной включениями льда ωi, и влажности

между включениями льда ωm. Суммарную влажность выражают в

долях единицы и определяют отношением массы всех видов

содержащихся в нем воды и льда (в прослойках и порах) к массе

скелета грунта.

Суммарная влажность определяется по формуле:

?????????????????????????? ωtot = ωi + ωm??????????????? (5.38)

льдистость мерзлого грунта Ii— это отношение содержащихся в нем

объема льда к объему мерзлого грунта (с включением льда) и

определяется по формуле:

??????????????????????????????? ??????? (5.39)

где ρi— плотность льда, принимается равной 0,9 г/см3.

Н.А. Цытович (1973) мерзлые грунты по льдистости подразделяет

на три категории: сильнольдистые, слабольдистые и льдистые.

К сильнольдистым (льдистость более 50%) относятся суглинки и

глины, переходящие при оттаивании в текучее, текучепластичное

или мягко-пластичное состояние. Сильнольдистые грунты обладают

малой несущей способностью в оттаявшем состоянии и большой

сжимаемостью.

Слабольдистые (льдистостью менее 25%) суглинки и глины

приобретают обычно тугопластичную или полутвердую

консистенцию и обладают малой сжимаемостью.

Льдистые (льдистость 25—50%) грунты имеют свойства

промежуточные между двумя выше приведенными категориями.

Количество незамерзшей воды в мерзлых грунтах ωω, если

отсутствуют опытные данные, допускается ориентировочно

определять по формуле СниПа:

????????????? (5.40)

где кω — коэффициент, зависящий от числа пластичности Jp и

температуры грунта (табл. 5.9);

ωр — влажность грунта на границе раскатывания.

Таблица 5.9. Значения коэффициента kω

Грунты Число пластичности Jp

Температура грунта, °С

-0,3 -0,5 -1 -3 -5 -10

Пески и супеси Jp≤ 0,02 0 0 0 0 0 0

Супеси 0,02 <Jp≤ 0,07 0,6 0,50 0,40 0,33 0,28 0,25

Суглинки 0,07 <Jp<0,13 0,7 0,65 0,60 0,48 0,43 0,40

Суглинки 0,13 <Jp<0,17 * 0,75 0,65 0,53 0,48 0,45

Глины Jp>0,17 * 0,95 0,90 0,63 0,58 0,55

* Примечание. Вся вода в порах грунта не замерзает.

Мерзлые грунты, как и глины, характеризуются не только

вещественным составом, но и определенным строением, т.е.

размером, формой, характером пространственного

взаиморасположения составных частей. Для мерзлых грунтов

различают следующие основные текстуры: слитную, слоистую и

ячеистую.

Слитная (массивная) текстура (рис. 5.26,а) характеризуется

отсутствием видимых невооруженным глазом ледяных тел (линз,

прослоек и т.д.) в грунте. Грунты слитной текстуры в мерзлом

состоянии обладают, как правило, высокой прочностью, а при

оттаивании их прочностные свойства снижаются в меньшей

степени, чем у грунтов со слоистой или ячеистой текстурами.

Рис. 5.26. Основные виды текстуры мерзлых грунтов: а — слитная

(массивная); б — слоистая; в — ячеистая (сетчатая)

Слоистая текстура (см. рис. 5.26,б) возникает при одностороннем,

медленном промерзании преимущественно глинистых грунтов,

обладающих высокой влажностью. Грунты со слоистой текстурой

обладают достаточно высокой прочностью, но при оттаивании их

прочностные показатели резко падают.

Ячеистая (сетчатая) текстура (рис. 5.26,в) возникает в тех случаях,

когда ледяные тела различного размера, формы и ориентировки

образуют более или менее непрерывную сетку или решетку.

Из механических свойств мерзлых грунтов наибольшее значение

имеют величина относительного сжатия εth при переходе мерзлого

грунта в талое состояние и сопротивление сжатию (σсж).

Относительное сжатие определяют путем испытания грунта в

компрессионном приборе и рассматривают по формуле

???????????? ?(5.41)

где hƒ и hth — высота образца, находящегося в мерзлом и талом

состояниях при неизменном давлении.

При оценке механических свойств расчетное сопротивление сжатию

(σсж) засоленных мерзлых грунтов принимают по табл. 5.10, а

сцепление (с) мерзлых грунтов ненарушенной структуры дано в

табл. 5.11.

Таблица 5.10. Расчетные сопротивления сжатию засоленных

мерзлых грунтов σсж> МПа

Грунт Засоленность грунта J

Температура грунта, °С

-1 -2 -3 -4

Песок:

пылеватый

мелкий и средний

0,05

0,10

0,30

0,50

0,10

0,20

0,50

0,75

0,60

0,30

0,80

0,40

1,30

0,50

0,25

0,15

1,20

0,80

0,40

1,60

0,90

0,55

0,20

1,40

1,10

0,60

0,35

1,80

1,30

0,65

0,30

1,70

1,40

0,80

0,45

Супесь 0,20

0,50

0,75

0,50

0,75

0,40

1,30

0,70

0,20

1,5

0,9

0,3

Суглинок 0,50

0,20

1,00

0,45

0,25

0,15

0,65

0,35

0,22

1,20

0,65

0,30

1,20

0,95

0,50

Глина 0,25

0,50

1,00

0,45

0,25

0,15

0,65

0,35

0,22

1,10

0,65

0,30

1,20

0,95

0,50

Таблица 5.11. Сцепление мерзлых грунтов ненарушенной

структуры при мгновенном см и длительном сд действии

нагрузки, МПа

Грунт Влажность,ω

Температура грунта, -°С

0,3-0,4 1,1-1,2 4,0-4,2

Величина сцепления при

см сд см сд см сд

Песок 0,24 1,4 0,22 1,6 0,25 1,9 0,4

Песок

пылеватый

0,23 1,1 0,21 1,4 0,27 2 0,4

Супесь 0,28-0,34

0,40-

0,45

0,09-

0,10

0,73 0,16

0,8-

1,15

0,28-

0,32

Суглинок 0,36 0,43 0,06 0,7 0,1 1,2 -

Глина

ленточная

плотная

0,30-0,40 0,57 0,18 - 0,26 0,16 0,42

Фундаменты на структурно-

неустойчивых % грунтах

При строительстве и эксплуатации городских зданий и

сооружений на структурно-неустойчивых грунтах при

определенных инженерно-геологических условиях

зафиксированы многочисленные случаи образования резко

выраженных неравномерных осадок, которые часто приводили к

полному разрушению. К структурно-неустойчивым грунтам

относятся лёссовые грунты, грунты, находящиеся в мерзлом и

вечномерзлом состоянии, рыхлые пески, илы, чувствительные

пылеватолинистые грунты, а также пылевато-глинис-тые

набухающие грунты.

Развитие значительных неравномерных осадок в структурно-

неустойчивых грунтах происходит из-за нарушения их

природной структуры, которое возможно в результате

механических и физических воздействий.

Механические воздействия обусловлены приложением внешней

нагрузки от фундаментов, а также различными динамическими

явлениями (вибрация, колебания и т. п.), происходящими в

результате движения транспорта, технологических,

производственных и других факторов. К механическим

воздействиям наиболее чувствительны несвязные и слабосвязные

грунты, а именно, слабые насыщенные водой пылевато-

глинистые грунты, илы, заторфованные грунты, рыхлые пески и

др.

Физические воздействия, при которых происходит нарушение

структуры грунтов, обусловлены дополнительным увлажнением,

которое может оказать неблагоприятное влияние на лёссовые и

набухающие грунты; оттаиванием мерзлых и вечномерзлых

грунтов, а также химической а механической суффозией и

выветриванием. Данный тип воздействий приводит к увеличению

деформативности вследствие разрушения структурных связей,

вызывая дополнительные неравномерные осадки.

В структурно-неустойчивых грунтах при приложении внешней

нагрузки разрушение структурных связей происходит быстрее,

чем образование новых, в отличие от структурно-устойчивых

грунтов, в которых одновременно с частичным нарушением

структуры и уплотнения возникают новые связи, увеличивая тем

самым их прочность. Поэтому в структурно-неустойчивых

грунтах процесс разрушения структурных связей происходит

лавинообразно и приводит к развитию просадки, не связанной с

процессом постепенного уплотнения.

Возведение и эксплуатация сооружений на структурно-

неустойчивых грунтах весьма затруднительны, поэтому при

проектировании необходимо учитывать условия, при которых

возможно нарушение их природной структуры и развитие

просадки, и принимать меры, направленные на устранение таких

неблагоприятных явлений.

Следует отметить, что основания, сложенные структурно-

неустойчивыми грунтами при нагрузках, напряжения от которых

не превышают структурной прочности, обладают в некоторых

случаях удовлетворительными физико-механическими

характеристиками, которые резко ухудшаются при нарушении

структуры или превышения напряжениями структурной

прочности.

3. Напряжение в грунтовых массивах, закон

уплотнения

Основы напряженного состояния грунтов оснований

При определении напряжений в основаниях сооружений массива грунта

обычно рассматривают как полупространство 0 ≤ z < ∞, ограниченное

горизонтальной плоскостью z = 0. Грунт считают находящимся в

сложном напряженно-деформированном состоянии и линейно-

деформированном, поэтому для него справедливо основное положение

закона Гука — линейность связи между напряжениями и деформациями.

Однако при действии внешних сил с давлениями, превышающими

структурную прочность грунта, возникают не только упругие, но и

значительно большей величины остаточные (пластические) деформации.

Напряжения в массивах грунтов возникают как под действием внешних

нагрузок, так и от собственного веса грунта. Знание напряжений

необходимо для расчетов деформаций грунтов, обусловливающих

осадки и перемещения зданий и сооружений для оценки прочности,

устойчивости грунтов и давления на ограждения.

Без учета распределения напряжений в грунте невозможно, например,

рассчитать осадки насыпей, устоев мостов, акведуков, лотков,

фундаментов искусственных и других сооружений.

Распределение напряжений в грунтовой толще зависит от следующих

факторов: характера и режима нагружения массива, инженерно-

геологических и гидрогеологических особенностей площадки

строительства, состава и физико-механических свойств грунтов.

Давление от нагрузки, приложенной к поверхности грунтового массива,

передается в грунте частицами или структурными агрегатами через

точки контакта, распределяясь по мере углубления в грунт на все

большую площадь.

Чтобы уяснить характер распределения напряжений, сделав допущение,

представим себе грунт состоящим из одинаковых по форме и размерам

твердых частиц (упрощающая модель), уложенных рядами друг на

друге, как показано на рис. 6.1.

Рис. 6.1. Пример модели дискретной среды из одинаковых шаров: а —

схема укладки; б — схема передачи (распределения) внешней

сосредоточенной силы на частицы грунта

Как видно из рис. 6.1, на II ряд действует вес частиц I ряда, а на III ряд

— частицы I и II ряда и т.д. Согласно рис. 6.1,б, внешняя

сосредоточенная сила действует на одну частицу I ряда, которая в свою

очередь воздействует на две частицы П.

Таким образом, с увеличением глубины количество твердых частиц, на

которые передается давление, увеличивается и в свою очередь

происходит рассеивание напряжений (см. рис. 6.1), т.е. напряжение от

приложенной внешней силы распределяется в массиве под некоторым

углом.

При оценке напряжений, действующих в грунтах, реальные силы,

приложенные к отдельным грунтовым частицам, заменяют

воображаемыми силами, распределенными по всему объему или

сечению грунтового массива.

Величину этих сил, отнесенных к единице площади сечения массива, и

принимают условно за величину напряжений в грунте.

Формирование напряжений в грунтовой толще происходит не мгновенно

при приложении нагрузки, а может развиваться весьма длительное

время. Это связано со скоростью проектирования деформаций и

особенно сильно проявляется в глинистых грунтах, где процессы

фильтрационной консолидации (консолидация — процесс уплотнения

грунта по мере удаления воды из его пор) и ползучести развиваются

очень медленно.

Изучение напряженного состояния грунта можно проводить по двум

направлениям:

экспериментальным путем, измеряя непосредственно давления в грунте

при помощи специального оборудования;

теоретическим путем, используя методы теории упругости, так как здесь

мы имеем дело с объемным напряженным состоянием грунтов.

Работа грунта основания существенно отличается от работы материала

строительной конструкции, сооружений и т.д. Отличия состоят в

следующем:

грунты имеют малую прочность и большую деформируемость по

сравнению с материалами конструкций; прочность их в десятки и сотни

раз больше по сравнению с грунтом основания, а деформируемость,

наоборот, меньше;

деформация грунта во времени при постоянной нагрузке возрастает

(например, для глинистых грунтов процессы консолидации и

ползучести) (рис. 6.2).

Рис. 6.2. Деформация грунта во времени

Как было сказано выше, деформация глинистых грунтов может длиться

годами и даже десятки лет;

неоднородность грунтов и их свойств в основании фундаментов, а

следовательно, прочности и деформируемости (понятие

анизотропность), т.е. неодинаковые свойства грунтов в различных

направлениях;

неоднородность напряжений в грунтовой толще в естественных

условиях и сложность их изменений под действием внешней нагрузки;

различие закономерностей изменения напряженного состояния грунтов,

однородных по составу, но при различной величине внешней нагрузки

(график Герсеванова).

Работа оснований сооружений рассматривается применительно к

плоской, пространственной, осесимметричной или контактной задаче в

зависимости от принятой расчетной схемы.

По схеме плоской задачи рассчитываются ленточные фундаменты,

основания подпорных стен, насыпей, дамб, а также фундаменты плит

водосливных плотин, шлюзов, сухих доков и т.д.

Таким образом, по этой схеме напряжения распределяются в одной

плоскости, а в перпендикулярном направлении они будут равны нулю

или постоянны (рис. 6.3).

Рис. 6.3. Схема к плоской задаче

По схеме осевой симметрии (рис. 6.4) рассчитываются фундаменты

водонапорных башен, доменных печей, фабричных труб, днища

резервуаров, газгольдеров и т.д.

Рис. 6.4. Схема к осесимметричной задаче

По схеме пространственной задачи рассчитываются фундаменты под

отдельные колонны и сплошные фундаментные плиты под сетку колонн.

Закон уплотнения и линейная деформируемость грунта

Поскольку уравнение (2.3) описывает изменение коэффициента

пористости ei лишь в пределах секущей АВ (см. рис. 2.2, б), оно

дает приближенную зависимость между коэффициентом пористости

и давлением. Для большого диапазона изменения давления

компрессионная кривая первичного сжатия (прямая CD на рис.

2.3,6) описывается логарифмической зависимостью

(2.5)

где ei — коэффициент пористости при давлении pi; е0 — начальный

коэффициент пористости грунта; Сс — коэффициент компрессии

(параметр кривой); р0 — давление, при котором начинается

первичное сжатие грунта.

Продифференцировав выражение (2.5), получим

de=- Ck dp/p,

где Ck —постоянная величина.

Следовательно, при первичном сжатии изменение коэффициента

пористости грунта прямо пропорционально изменению давления и

обратно пропорционально суммарному давлению. Эту зависимость

применяют либо при рассмотрении деформаций очень слабых

грунтов, либо при изменении давления в значительных пределах.

Давление в грунте основания промышленных и гражданских зданий

и сооружений обычно изменяется в небольших пределах. Чаще

всего оно повышается не более чем до 0,3 МПа и в редких случаях

до 0,6 МПа. При таких давлениях секущая АВ (см. рис. 2.2, б)

близка к кривой, т. е. для расчетов можно пользоваться уравнением

(2.3). Продифференцировав его, получим

de =— m0 dp. (2.3')

Поэтому закон компрессии грунта формулируется так: изменение

коэффициента пористости грунта прямо пропорционально

изменению давления.

Линейная деформируемость грунта в пределах небольших

изменений давления вытекает из выражения (2.4'). Действительно,

из (2.4') следует:

mv pi =si / h

Правая часть этого равенства является относительной деформацией

грунта. Поскольку для определенного грунта и данного изменения

давления величина mv постоянна, относительная деформация

грунта прямо пропорциональна давлению. Следовательно, грунт

можно считать линейно деформируемым телом.

Однако в ряде случаев это положение приводит к значительным

расхождениям между рассчитанными и наблюдаемыми в натуре

деформациями. Поэтому в последнее время исследователи

стремятся учесть нелинейную зависимость между напряжениями и

деформациями. Однако такие решения еще не вошли в инженерную

практику и требуют дополнительных разработок.

4.Сопротивление грунтов сдвигу . Прочностные

характеристики грунтов.

Изучение сопротивления грунтов сдвигающим усилиям,

возникающим в результате воздействия различных инженерных

сооружений, имеет большое значение для правильного расчета

устойчивости оснований (несущей способности оснований), оценки

устойчивости откосов, расчета давления грунтов на подпорные

стенки и других инженерных расчетов.

В настоящее время нет единой точки зрения на природу

сопротивления глинистых пород сдвигу. Одни исследователи

считают, что сопротивление глинистых пород сдвигу обусловлено

только сцеплением между частицами, показателем которого

является коэффициент сцепления. Другие полагают, что

сопротивление глинистых пород сдвигу зависит как от сил трения,

так и от сил сцепления. Показателями сил трения, действующих в

грунте, считают угол внутреннего трения и коэффициент трения.

Вследствие неясности природы сопротивления глинистых пород

сдвигу и условности разделения его на внутреннее трение и

сцепление, некоторые исследователи предлагают вообще отказаться

от такого разделения и характеризовать сопротивление глинистых

пород сдвигу так называемым углом сдвига φ соответственно

тангенс этого угла называют коэффициентом сдвига tgφ.

Сопротивление сдвигу одного и того же грунта непостоянно и

зависит от физического состояния грунта - степени нарушенности

естественной структуры, плотности, влажности, а также от условий

производства испытаний (конструкция прибора, размеры образца,

скорость сдвига и т. д.). Для получения наиболее достоверных

данных испытания на сдвиг должны всегда проводиться в условиях,

максимально приближающихся к условиям работы грунта под

сооружением или в самом сооружении.

Показатели сопротивления грунта сдвигу определяются различными

способами, среди которых можно выделить три группы:

•? способы определения сопротивления сдвигу по одной или двум

заранее фиксированным плоскостям в сдвиговых приборах;

•? способы определения сопротивления сдвигу путем раздавливания

при одноосном и трехосном сжатии;

•? способ определения сопротивления сдвигу по углу естественного

откоса.

Способы первой группы могут быть в свою очередь разделены на

две подгруппы:

а) способы поперечного сдвига с конечной плоскостью сдвига;

б) способы кольцевого сдвига с бесконечной (замкнутой)

плоскостью сдвига.

Лабораторные испытания грунтов для определения показателей

трения и сцепления способом поперечного сдвига производят путем

среза нескольких образцов исследуемого грунта. При этом в

зависимости от характера предварительной подготовки образцов к

опыту различают:

а) сдвиг нормально уплотненных образцов (завершенное

уплотнение), когда образцы перед опытом предварительно

уплотняются под разными нагрузками до окончания процесса

консолидации; срез каждого образца производится при той же

вертикальной нагрузке, под которой он предварительно уплотнялся;

б) сдвиг переуплотненных образцов, когда образцы предварительно

уплотняются до окончания процесса консолидации, а сдвигаются

без нагрузки или при меньших нагрузках;

в) сдвиг недоуплотненных образцов (незавершенное уплотнение),

когда образцы предварительно не уплотняются или уплотняются в

продолжение короткого времени, за которое не наступает полная

консолидация; срез производится при различных вертикальных

нагрузках.

В зависимости от скорости приложения сдвигающего усилия в

процессе опыта различают медленный сдвиг и быстрый сдвиг. При

медленном сдвиге сдвигающую силу увеличивают только после

прекращения деформации, вызванной предыдущей ступенью

этой силы. При быстром сдвиге увеличение сдвигающей силы

производят быстро, не дожидаясь прекращения деформаций

Прочностные характеристики грунтов .

Показатели физических свойств грунтов определяются либо на

отобранных в натуре в массиве образцах грунтов, либо

непосредственно путем испытания грунтов, находящихся в

грунтовом массиве, то есть в полевых условиях. При испытаниях

следует выполнять требования соответствующих ГОСТов, если

они имеются, или ведомственных нормативных документов. Для

испытаний используются стационарные либо полевые

лаборатории. Предпочтительными являются прямые методы

испытаний, но в ряде случаев используются результаты

косвенных методов исследования.

Минимально достаточным для последующего осреднения

результатов в математической статистике принято считать 6

определений. Однако, чем большее количество результатов

определений введено в формулу для статистического нахождения

среднего значения, тем "точнее" оказывается результат. В

обработку вводятся результаты одной статистической

совокупности, характеризующей данный массив. Если

прослеживается закономерность в изменении частных

интересующих нас значений показателя от точки к точки в одном

направлении, то тогда их нельзя обычным путем вводить в одну

статистическую совокупность.

Показатели (характеристики) физических свойств грунтов

определяются как нормативные.

Нормативными считаются средние значения показателей или

характеристик, определяемые как среднеарифметические.

Виды испытаний прочностных характеристик

грунтов:

Испытания на сдвиговом приборе – при прямом плоскостном

срезе цилиндрического образца грунта выполняется в

лабораторных условиях.

Испытания в приборе трехосного сжатия (стабилометре).

Методика проведения испытаний с наибольшей полнотой

отражает работу грунта в основании. При загружении грунта в

приборе создается трехосное напряженное состояние с

измерением каждого компонента напряжения. Конструкция

прибора позволяет определить: нейтральное или поровое

давление по манометру, продольную и поперечную деформацию

образца, изменение объема образца по валюмометру.

Помимо прочностных характеристик на этом приборе можно

определить деформационные характеристики (коэффициент

Пуассона, модуль деформации).

Испытания при одноосном сжатии. Проводятся для

тугопластичных и твердых глин, которые хорошо сохраняют

форму после обработки образцов. Образцы изготавливают в

форме цилиндра с соотношением размеров h=(1,5 – 2,0) d.

Разрушение образцов будет происходить как у хрупких

материалов по плоскости, где касательные напряжения достигают

предельного сопротивления сдвигу. Угол наклона этой плоскости

стремится к 45 градусов.

Лопастные испытания – проводятся в полевых условиях для

грунтов, из которых трудно отбирать образцы без нарушения

природного строения (торф, илы, глинистые водонасыщенные

грунты). Для испытания откапывается небольшой шурф, в грунт

вдавливается крестовина прибора и фиксируется крутящий

момент, при котором происходит срез грунта лопастью по

цилиндрической поверхности. Результаты испытаний

используются для расчета ула внутреннего трения и сцепления.

Метод шарикового штампа. Применяется для определения

сцепления для связных грунтов (глинистых) и вязких (льдистых,

вечномерзлых). Испытания состоят во вдавливании в

исследуемый грунт сферического штампа постоянной нагрузкой

Р и измерении во времени осадки S. Расчетное сопротивление

вычисляется по формуле:

DSРC



/18,0

, где В – диаметр штампа.

Испытания на сдвиг в шурфах. Применяются в основном для

крупнообломочных грунтов, из которых невозможно отобрать

для лабораторных испытаний. Эти испытания аналогичны

испытаниям в сдвиговом приборе.

18. Деформационные характеристики грунтов с жесткими

связями (модуль Юнга, коэффициент Пуассона).

19. Понятия сцепления и внутреннего трения.

5.Коэффициент фильтрационной

консолидации

Деформации грунта являются результатом процессов, проте-

кающих под влиянием напряженного состояния, созданного в

грунте внешней нагрузкой. Внешние нагрузки, приложенные к

грунту, вызывают взаимное перемещение твердых минеральных

частиц, их структурных агрегатов. При последовательном

увеличении нагрузки на грунт наблюдается три стадии его

напряженного состояния: 1) стадия уплотнения; 2) стадия

сдвигов; 3) стадия разрушений или стадия выпирания. В первой

стадии наблюдается уплотнение грунта, и скорость деформации с

течением времени уменьшается, приближаясь к нулю. В этой

стадии зависимость между напряжениями и деформациями с

достаточной точностью может быть принята линейной.

Пластические деформации вызывают в грунте изменение

свойств, размеров и форм частиц. Грунтовое тело становится

неспособным возвращаться в первоначальное состояние,

появляются так называемые остаточные деформации,

зависимость между напряжениями и деформациями теряет свой

линейный характер. Третья стадия характеризуется интенсивным

возрастанием скорости деформаций и выпиранием грунта в

стороны от периметра фундамента. Деформации возникают

внезапно и катастрофически растут. Осадки этой фазы являются

значительными. В конечном итоге в грунтах могут иметь место

следующие виды деформаций: 1) упругие, возникающие в

результате перемещений узлов кристаллической решетки

минералов; 2) остаточные, которые обусловлены: а)

адсорбционными явлениями (изменение толщины водных пленок

в контактах между структурными элементами); б) изменением

взаимного расположения структурных элементов; в)

пластическими деформациями? необратимые перемещения

элементов кристаллической решетки минералов); г)

псевдопластическими деформациями, происходящими в текучих

и глинистых грунтах без изменения их объема.

6. Водопроницаемость грунтов.

В грунтах часть его объема занимают твердые минеральные частицы, а

другую часть — поры, которые обусловливают водопроницаемость.

Различные виды грунтов обладают разной водопроницаемостью. При

прочих равных условиях лучшей водопроницаемостью обладают

песчаные грунты и меньшей — глинистые.

Водопроницаемостью грунта называют его способность пропускать

через себя свободногравитационную воду под действием разности

напоров. От водопроницаемости грунтов зависит ряд процессов,

влияющих на устойчивость сооружений, в том числе:

скорость уплотнения основания (грунтов);

суффозия грунта — перемещение или вынос мелких частиц по порам,

образованным более крупными частицами под воздействием

фильтрационного потока;

оползневые явления — перемещение грунтовых масс под действием

силы тяжести или внешней нагрузки.

Движение свободногравитационной воды в грунтах оснований

называется фильтрацией. Фильтрация может происходить по различным

направлениям:

горизонтально (рис. 5.15,а);

вертикально вниз (рис. 5.15,6);

вертикально вверх (рис. 5.15,в).

Рис. 5.15. Схемы движения воды в фунтах: l — длина или высота

образца грунта; ΔН — разность отметок воды перед входом в образец и

выходом из него

Таким образом, движение воды в грунте происходит под действием

возникающего в нем градиента напора.

Движение воды в песчаных и глинистых грунтах рассматривается как

параллельно-струйное, т.е. имеет ламинарный характер движения, так

как скорость фильтрации в таких грунтах невелика.

Первые эксперименты по изучению фильтрации воды были поставлены

французским инженером А. Дарси в 1854 г. Дарси установил, что объем

воды V, профильтровавшийся через заполненную песком трубу,

пропорционален площади ее поперечного сечения, потерям напора и

продолжительности фильтрации:

V = kfJAt,???????????? (5.29)

где kf — коэффициент фильтрации, см/с (м/сут);?J — гидравлический

градиент (уклон), равный потере напора на пути фильтрации:

??????????????? ???????? (5.30)

где kƒ — площадь поперечного сечения трубки, м2;

?t — продолжительность фильтрации, с.

Коэффициент фильтрации

Коэффициент фильтрации — это скорость фильтрации при

гидравлическом градиенте, равном единице. Он широко используется в

практике гидрогеологических расчетов, характеризует

водопроницаемость грунтов, зависит от грануломефического состава,

плотности и пористости грунта. Коэффициент фильтрации определяется

в лабораторных и полевых условиях.

Коэффициент фильтрации — это скорость фильтрации при

гидравлическом градиенте, равном единице. Он широко используется в

практике гидрогеологических расчетов, характеризует

водопроницаемость грунтов, зависит от грануломефического состава,

плотности и пористости грунта. Коэффициент фильтрации определяется

в лабораторных и полевых условиях.

Средние ориентировочные значения коэффициента фильтрации для

некоторых видов грунтов приведены в табл. 5.5.

Таблица 5.5. Ориентировочные значения коэффициента фильтрации

грунтов

Грунт

Коэффициент

фильтрации kƒ, м/сут.

Галечниковый (чистый) 200

Гравийный (чистый) От 100 до 200

Крупнообломочный с песчаным заполнителем От 100 до 150

Песок:

???? гравелистый

???? крупный

???? средней крупности

???? мелкий

???? пылеватый

От 50 до 100

От 25 до 75

От 10 до 25

От 2 до 10

От 0,1 до 2

Супесь От 0,1 до 0,7

Суглинок 0,005 до 0,4

Глина 0,005

Торф:

???? слаборазложившийся

???? среднеразложившийся

???? сильноразложившийся

От 1 до 4

От 0,15 до 1,0

От 0,01 до 0,15

Для хорошо фильтрующих грунтов (песков и супесей) коэффициент

фильтрации определяют с помощью прибора (рис. 5.16), состоящего из

трубы длиной l, заполненной грунтом, и двух трубок — подводящей и

отводящей воду. При разности напоров Н2 - Н1 вода будет

фильтроваться под действием градиента (J). Определив объем воды V,

профильтровавшейся за время t, можно по формуле

?????? (5.31)

Зависимость скорости фильтрации (Vƒ) от гидравлического фадиента,

характеризующего водопроницаемость фунтов, носит название закона

ламинарной фильтрации. Математическое выражение этого закона,

предложенное Дарси, имеет вид

???????? ?????????? (5.32)

Рис. 5.16. Схема установки для определения коэффициента фильтрации

Формулируется закон ламинарной фильтрации следующим образом:

скорость движения (фильтрации) воды в грунте прямо пропорциональна

гидравлическому градиенту.

Фильтрация воды в вязких глинистых грунтах имеет свои особенности,

связанные с малыми размерами пор и вязким сопротивлением

водноколлоидных пленок, обволакивающих минеральные частицы

грунтов.

Движение (фильтрация) воды в глинистых грунтах, в отличие от

песчаных (рис. 5.17, кривая а), начинается лишь при достижении

некоторого градиента напора (см. рис. 5.17, кривая б),

преодолевающего внутреннее сопротивление движения воды.

Рис. 5.17. Зависимость скорости фильтрации в грунте от

гидравлического градиента

Для кривой (б) различают три участка:

?? I — начальный (0—1), когда скорость фильтрации практически

равна нулю (Vf = 0);

? II — переходный (1—2) криволинейный участок;

? III — прямолинейный (2—3), характеризующий процесс

установившейся фильтрации.

Таким образом, в глинистых грунтах, особенно в плотных, при

относительно небольших значениях градиента напора фильтрация

может не возникать (участок 0—1, кривая б). Увеличение градиента

напора приведет к постепенному, очень медленному развитию

фильтрации (участок 1—2). Наконец, при некоторых значениях

гидравлического градиента устанавливается постоянный режим

(участок 2—3).

Напорный градиент, до достижения которого фильтрация в грунте

не наблюдается, называется начальным градиентом (J'0).

Во многих случаях исключают из рассмотрения участок 0—2

кривой «б» и закон ламинарной фильтрации для глинистых грунтов

принимают в виде

?????? ?????????? (5.33)

где J'0 — начальный градиент напора, т.е. участок на оси J,

отсекающий продолжение отрезка прямой 2—3 до пересечения с

этой осью. Для песчаных грунтов фильтрация начинается сразу

после передачи напора (рис. 5.17, кривая а).

7.Теория фильтрационной консолидации

Деформации грунта являются результатом процессов, протекающих

под влиянием напряженного состояния, созданного в грунте

внешней нагрузкой. Внешние нагрузки, приложенные к грунту,

вызывают взаимное перемещение твердых минеральных частиц, их

структурных агрегатов. При последовательном увеличении нагрузки

на грунт наблюдается три стадии его напряженного состояния: 1)

стадия уплотнения; 2) стадия сдвигов; 3) стадия разрушений или

стадия выпирания. В первой стадии наблюдается уплотнение

грунта, и скорость деформации с течением времени уменьшается,

приближаясь к нулю. В этой стадии зависимость между

напряжениями и деформациями с достаточной точностью может

быть принята линейной. Пластические деформации вызывают в

грунте изменение свойств, размеров и форм частиц. Грунтовое тело

становится неспособным возвращаться в первоначальное состояние,

появляются так называемые остаточные деформации, зависимость

между напряжениями и деформациями теряет свой линейный

характер. Третья стадия характеризуется интенсивным возрастанием

скорости деформаций и выпиранием грунта в стороны от периметра

фундамента. Деформации возникают внезапно и катастрофически

растут. Осадки этой фазы являются значительными. В конечном

итоге в грунтах могут иметь место следующие виды деформаций: 1)

упругие, возникающие в результате перемещений узлов

кристаллической решетки минералов; 2) остаточные, которые

обусловлены: а) адсорбционными явлениями (изменение толщины

водных пленок в контактах между структурными элементами); б)

изменением взаимного расположения структурных элементов; в)

пластическими деформациями? необратимые перемещения

элементов кристаллической решетки минералов); г)

псевдопластическими деформациями, происходящими в текучих и

глинистых грунтах без изменения их объема.

8. Напряжение от собственного веса грунта.

Фактическое напряженное состояние грунтов основания при

современных методах изысканий определить не представляется

возможным. В большинстве случаев ограничиваются вычислением

вертикальных напряжений, возникающих от веса вышележащих

слоев грунта. Эпюра этих напряжений по глубине однородного слоя

грунта будет иметь вид треугольника. При слоистом напластовании

эпюра ограничивается ломаной линией, как показано на рис. 9

(линия abсde).

На глубине z вертикальное напряжение будет равно:

где γ0i — объемный вес грунта i-го слоя в т/м3; hi — толщина i-го

слоя в м; п — число разнородных слоев по объемному весу в

пределах рассматриваемой глубины z. Объемный вес

водопроницаемых грунтов, залегающих ниже уровня грунтовых вод,

принимается с учетом взвешивающего действия воды:

здесь γу — удельный вес твердых частиц грунта в т/м3; ε —

коэффициент пористости грунта природного сложения.

При монолитных практически водонепроницаемых глинах и

суглинках в случаях, когда они подстилаются слоем

водопроницаемого грунта, имеющего грунтовые воды с

пьезометрическим уровнем ниже уровня грунтовых вод верхних

слоев, учет взвешивающего действия воды не производится. Если

бы в напластовании грунтов, изображенном на рис. 9, четвертый

слой представлял собой монолитную плотную глину и в

подстилающем водоносном слое грунтовая вода имела бы

пьезометрическим уровень ниже уровня грунтовой воды верхнего

слоя, то поверхность слоя глины являлась бы водоупором,

воспринимающим давление от слоя воды. В таком случае эпюра

вертикальных напряжений изобразилась бы ломаной линией

abcdmn, как показано на рис. 9 пунктиром.

Следует отметить, что под действием напряжений от собственного

веса природного грунта деформации основания (за исключением

свежеотсыпанных насыпей) считаются давно загасшими. При

большой толще водонасыщенных сильносжимаемых грунтов,

обладающих ползучестью, иногда приходится считаться с

незавершенной фильтрационной консолидацией и консолидацией

ползучести. В таком случае нагрузку от насыпи нельзя считать за

нагрузку от собственного веса грунта.

9.Напряжения от вертикальной

сосредоточенной силы

М.7.1. Решение какой задачи теории упругости для

полупространства является основным? Чем обусловлена

возможность использования его для решения других практически

важных задач?

Основным является решение задачи о сосредоточенной силе,

приложенной к поверхности полупространства перпендикулярно

к граничной плоскости (задача Буссинеска). Для решения задач о

нагрузке, имеющей горизонтальную составляющую,

рассматривается дальнейшее развитие решения этой же задачи,

но при сосредоточенной силе, действующей вдоль граничной

плоскости (как бы "прикрепленной" к ней в одной точке, рис.

М.7.1.). Аналогичные решения задач о сосредоточенных силах

вертикальной и горизонтальной, то есть приложенных

перпендикулярно (решение Фламана) и по касательной к границе

полуплоскости, также являются основными. Из них путем

интегрирования могут быть получены многие решения

интересующих нас в практических целях задач.

Рис.М.7.1. Схема приложения сосредоточенных сил при

рассмотрении основных задач теории упругости

М.7.2. Чему равны напряжения непосредственно под

сосредоточенной силой? Какое предположение делается в

отношении зоны, расположенной непосредственно у

сосредоточенной силы?

Задача эта является абстрактной, так как в действительности

усилия всегда распределяются по некоторой площадке.

Непосредственно под сосредоточенной силой напряжения

являются бесконечно большими. Предполагается, что сплошная

среда является бесконечно прочной и не может разрушаться.

Буссинеск, чтобы обойти это обстоятельство, не рассматривал

небольшую зону, непосредственно находящуюся у

сосредоточенной силы.

М.7.3. Каковы граничные условия в задаче о сосредоточенной

силе на полупространстве?

В месте приложения сосредоточенной силы, непосредственно

совпадающем с началом координат (так проще решить задачу),

действует эта сила, а во всех остальных точках границы никаких

сил не действует. В точках, бесконечно удаленных от места

приложения силы, напряжения должны стремиться к нулю.

М.7.4. Каким образом напряжение s R зависит от угла, радиуса,

величины силы? Сколько координат участвует в решении этой

задачи и какие?

Напряжениеs R является основным. Это напряжение

пропорционально косинусу угла между радиусомвектором и

вертикалью, обратно пропорционально квадрату радиуса и прямо

пропорционально величине действующей силы. В решении этой

задачи, вследствие имеющейся симметрии, участвуют две

координаты - радиус и угол между ним и вертикалью.

М.7.5. Из каких условий определяется безразмерный

коэффициент в формуле для s R в задаче о сосредоточенной силе

на полупространстве?

Из условия равновесия при проектировании всех сил на

вертикальную ось. Вырезается полусфера и на вертикальную ось

проектируются все напряжения s R, умноженные на

элементарные площадки (чтобы получить элементарные силы).

Эти проекции должны уравновешиваться силой, действующей

сверху вниз на полупространство (рис.М.7.5).

М.7.6. Как можно воспользоваться теорией размерностей для

решения задачи о сосредоточенной силе?

Поскольку напряжение s R зависит от величины силы P, угла

между вертикалью и радиусом q , а также радиуса R, то,

учитывая, что напряжение должно быть пропорционально силе,

она попадает в числитель. Далее выбирается тригонометрическая

функция от угла q , четная, не зависящая от знака q , имеющая

максимум при q =0 и равная нулю при q =± p /2. Такой

простейшей функцией является cosq . Естественно, что этот

множитель попадает также в числитель. Поскольку напряжение s

R с увеличением расстояния от точки приложения силы должно

убывать, то радиус R должен попасть в знаменатель. Однако для

того, чтобы уравнять разномерности (слева H/м2, а справа, если R

в знаменателе в первой степени, то Н/м, а если во второй степени,

то H/м2), необходимо записать R в квадрате, откуда получим

Коэффициент A определяется в соответствии с ответом на вопрос

М.7.5. и равен A=3/2p .

М.7.7. Как получить напряжение sz, зная напряжение s R?

Если известно s R, то из условия равновесия элемента мы имеем в

данном случае s z=s Rcos2q .

М.7.8. Какой вид имеют эпюры напряжений szв задаче о

сосредоточенной силе?

Эпюры напряжений s z изображены на рис.М.7.8.

Рис.М.7.8. Эпюры напряжений s z в полуплоскости и

полупространстве по вертикальным и горизонтальному сечениям

М.7.9. Каким образом привести решение задачи о

сосредоточенной силе для напряжения s z к удобной табличной

форме?

Напряжение s z в координатах x,y,z имеет следующий вид:

Следует ввести обозначение , где r - проекция радиуса R на

граничную плоскость z = 0, а затем ввести относительную

координату r/z. Тогда получим

М.7.10*. Каким образом следует изменить решение о

сосредоточенной силе, нормальной к границе полупространства,

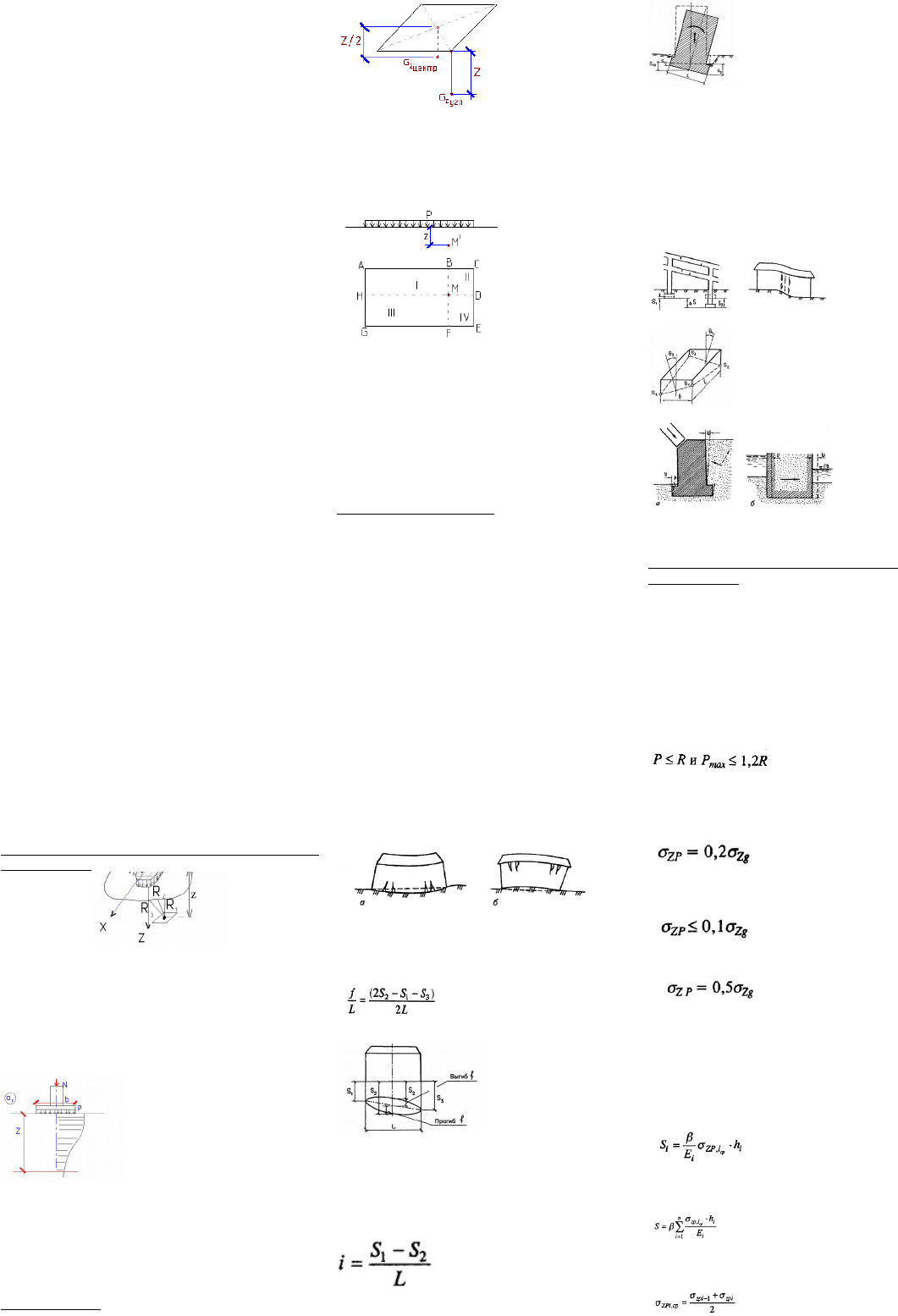
чтобы получить решение задачи о силе, действующей вдоль границы

полупространства?

Для вертикальной силы P имеем

для горизонтальной силы Q имеем

Таким образом, в функции одно из z заменяется на x. Для наклонной

силы следует учесть обе эти составляющие P и Q.

М.7.11. Как следует просуммировать напряжения, если действуют

несколько сосредоточенных сил?

Если действуют несколько сосредоточенных сил, то для одной силы Pi,

согласно ответу на вопрос М.7.9, имеем

При нескольких сосредоточенных силах получим

Коэффициенты Ki определяются каждый раз отдельно для своих

значений ri/z, так как радиус для каждой силы свой.

М.7.12*. Как строится решение задачи для силы, приложенной на

границе полуплоскости? Как соблюсти условие размерностей в этом

случае?

В случае плоской задачи решение строится таким же образом, как и в

пространственной задаче (см.вопрос М.7.9). В качестве аргументов

используются: сосредоточенная сила P (в случае плоской задачи она

имеет разномерность Н/м в отличие от пространственной, где

размерность силы в H), угол между радиусом и вертикалью q и радиус r.

Для того, чтобы левая и правая части имели одинаковые размерности,

числитель следует разделить не на квадрат радиуса, как в

пространственной задаче, а на радиус в первой степени. Следовательно,

получим

М.7.13*. Как определяется безразмерный коэффициент A1 в формуле

для s r (см.М.7.12) и в чем отличие в его определении по сравнению с

пространственной задачей?

Безразмерный коэффициент A1 определяется из условия равновесия

путем проектирования напряжений s r , умноженных на величину

элементарной площадки, на вертикальную ось. В данном случае берется

не полусфера, как в пространственной задаче, а полукольцо.

Коэффициент после интегрирования оказывается равным A1=2/p ,

поэтому

М.7.14. Как выглядят эпюры напряжений при действии сосредоточенной

силы в случае плоской задачи и чем они отличаются от эпюр

пространственной задачи?

Эпюры напряжений в случае плоской задачи имеют тот же вид, что и в

пространственной задаче, однако ординаты их другие. Напряжения в

случае плоской задачи рассеиваются как бы медленнее, чем в случае

пространственной задачи.

М.7.15. Какое условие накладывается на эпюры напряжений для

выполнения условия равновесия?

Для выполнения условия равновесия необходимо, чтобы в случае

пространственной задачи объем эпюры s z при заданной постоянной

величине z равнялся бы действующей сосредоточенной силе.

В случае плоской задачи это условие сохраняется, однако оно

упрощается, и поэтому площадь эпюры s z при постоянной величине z

должна быть равна внешней нагрузке.

10.Напряжения от распределенной нагрузки (метод

угловых точек)

В случае действия распределенной нагрузки напряжение в массиве

можно определить по формулам для нахождения напряжения при

действии сосредоточенной силы, используя принцип суперпозиции

(независимость действия сил)

Область загружения делится на ряд элементов, распределенная нагрузка

на которых заменяется равнодействующей в центрах их тяжести.

σz=(3/2)*π* (F1Z13/R15 + F2Z23/R25 +…+ FnZn3/Rn5)

или

σz=∑(FiKi/Z2)

Решение для определения σz под центром площади выглядит как:

σz=P*f*(z/(0.5b); a/b), где

b- ширина подошвы, a-длинна подошвы фундамента, z – глубина на

которой определяется напряжение, P- среднее давление под подошвой.

Значение f приводится в СНиП 2.02.01-83*, в виде таблиц. В них по двум

параметрам:

1) ξ=2z/b;

2) η=a/b.

Метод угловых точек.

В результате сравнения численных решений оказалось, что

напряжение под центром и под углом площади связанны

следующим образом:

σzугл/Z=0.25 σzцентр/(0,5z)

Для определения вертикального напряжения σz в любой точке

полупространства можно воспользоваться выражением

σz=0.25αP, где α- коэфф., принимаемый в зависимости от

отношения сторон площадей загружения a,b и глубины z.

Если проекция рассматриваемой точки M’ на горизонтальную

поверхность полупространства (точка М) располагается в пределах

площади загружения, то эту площадь можно разбить на 4

прямоугольника (ABMH, BCDM, DEFM, FGHM) так, что бы точка

M была угловой точкой каждого из них. Тогда напряжение σz

найдем суммированием напряжений под угловыми точками четырех

площадей загружения:

σz= σz1+ σz2 + σz3 + σz4=0,25(α1+α2 +α3 +α4)P

Так, пользуясь методом угловых точек, можно найти напряжение в

любой точке полупространства, к поверхности которого приложена

равномерно распределенная нагрузка в пределах прямоугольной

площади.

11.Деформации основания

Прогноз величины деформаций оснований на стадии

проектирования сооружения позволяет выбрать наиболее

правильные конструктивные решения фундаментов и надземных

частей зданий и сооружений. Осадки оснований оказывают

решающее влияние на прочность и устойчивость подземных

конструкций.

Осадкой называется медленная и сравнительно небольшая

деформация, происходящая в результате уплотнения грунта под

действием нагрузок и сопротивляющаяся коренным изменениям его

структуры.

При равномерных осадках основания подошва фундамента в любой

моент времени опускается на одинаковую величину. Такие осадки

не вызывают перераспределения усилий в конструкциях, но

затрудняют нормальную эксплуатацию.

При неравномерных осадках основания подошва фундамента

опускается на разную величину, вызывая перераспределение усилий

и деформаций в надземных частях зданий и сооружений. Такие

осадки ухудшают эксплуатацию оборудования, изменяют условия

устойчивости сооружений, вызывают перенапряжения в отдельных

конструкциях и элементах.

В зависимости от характера развития неравномерных осадок и от

жесткости здания или сооружения возникают следующие виды

деформаций.

Прогиб и выгиб возникают в протяженных зданиях и сооружениях,

не обладающих большей жесткостью.

В случае развития прогиба (рис. 7.1,а) наиболее опасная зона

растяжения находится в нижней части здания или сооружения,

выгибе (см. рис. 7.1,6), — наоборот, в верхней части сооружения.

Рис. 7.1. Схема прогиба (а) и выгиба (б) сооружения

Относительный прогиб или выгиб (ƒ/L) здания или сооружения

оценивается отношением стрелы прогиба или выгиба к длине

прогнувшейся части здания и кривизной изгибаемого участка (рис.

7.2) и определяется по формуле (по пособию к СНиП, 1986; СНиП

2.02.01—83):

?????? ?7.1.

где S1 и S3 — осадки в краях фундамента; S2 — наибольшая или

наименьшая осадка фундамента; L — длина фундамента.

Рис. 7.2. Относительный прогиб или выгиб сооружения

Крен (наклон) — поворот фундамента относительно горизонтальной

оси, проявляющийся при несимметричной загрузке основания.

Наибольшую опасность данный вид деформации представляет для

высоких сооружений — дымовых труб, узких зданий повышенной

этажности и др., т.е. характерен для жестких сооружений.

Крен рассматривается как разность абсолютных осадок двух точек

фундаментов, отнесенных к расстоянию между ними (рис. 7.3), и

определяется по формуле

???????????????? ?(7.2)

где S1 и S2 — осадки крайних точек сплошного фундамента или

двух фундаментов.

Рис. 7.3. Крен сооружения

Перекос зданий и сооружений характерен при резком проявлении

неравномерности осадок на участке небольшой протяженности

при сохранении относительной вертикальности несущих

конструкций (рис. 7.4).

Кручение возникает при неодинаковом крене здания или

сооружения по длине, при этом происходит развитие крена в

двух сечениях сооружения в разные стороны (рис. 7.5).

Горизонтальные перемещения фундаментов зданий или

сооружений возникают при действии на основания

горизонтальных нагрузок (рис. 7.6). Например, устои мостов

(рис. 7.6,а), гидротехнические сооружения (рис.7.6,б), они

возможны при развитии оползней и при выполнении подземных

выработок.

Рис. 7.4. Перекос сооружения

Рис. 7.5. Кручение сооружения

Рис. 7.6. Схема горизонтального перемещения устоя моста (а) и

гидротехнического сооружения (б)

12. Расчет осадок по методу послойного

суммирования.

Расчет осадки слоистых оснований выполняется методом

послойного суммирования, в основу которого положена выше

разобранная задача (основная задача). Сущность метода

заключается в определении осадок элементарных слоев

основания в пределах сжимаемой толщи от дополнительных

вертикальных напряжений σZP, возникающих от нагрузок,

передаваемых сооружениям.

Так как в основу этого метода положена расчетная модель

основания в виде линейно-деформируемой сплошной среды, то

необходимо ограничить среднее давление на основание таким

пределом, при котором области возникающих пластических

деформаций лишь незначительно нарушают линейную

деформируемость основания, т.е. требуется удовлетворить

условие

??????? ?(7.11)

Для определения глубины сжимаемой толщи Нс вычисляют

напряжения от собственного веса σZq и дополнительные от

внешней нагрузки σZP.

Нижняя граница сжимаемой толщи ВС основания принимается

на глубине z = Нс от подошвы фундамента, где выполняется

условие

? ???????????????? (7.12)

т.е. дополнительные напряжения составляют 20% от

собственного веса грунта.

При наличии нижеуказанной глубины грунтов с модулем

деформации Е≤5 МПа должно соблюдаться условие

??? ?????????????? ?(7.13)

Для оснований гидротехнических сооружений по СНиП 2.02.02—

85 «Основания гидротехнических сооружений» нижняя граница

активной зоны находится из условия

?????? ???????????????? (7.14)

Расчет осадки удобно вести с использованием графических

построений в следующей последовательности (рис. 7.11):

строят геологический разрез строительной площадки на месте

рассчитываемого фундамента;

наносятся размеры фундамента;

строятся эпюры напряжений от собственного веса грунта σZg и

дополнительного σZP от внешней нагрузки;

определяется сжимаемая толща Нс;

разбивается Нс на слои толщиной hi≤0,4b;

определяется осадка элементарного слоя грунта по формуле

?? ?

????????????????????????????????????????????????????????????????????????????????????????????? (7.15)

Тогда полную осадку можно найти простым суммированием

осадок всех элементарных слоев в пределах сжимаемой толщи из

выражения

??????????????? (7.16)

где β— безразмерный коэффициент, зависящий от коэффициента

относительных поперечных деформаций, принимаемый равным

0,8; hi — высота i-го слоя; Ei — модуль деформации i-го слоя

грунта;

— среднее напряжение i-го элементарного

слоя.

Метод послойного суммирования позволяет определять осадку не

только ценфальной точки подошвы фундамента. С его помощью

можно вычислить осадку любой точки в пределах или вне

пределов фундамента. Для этого пользуются методом угловых точек и

строится эпюра напряжений вертикальной, проходящей через точку, для

которой требуется расчет осадки.

Рис. 7.11. Расчетная схема для определения осадки методом послойного

суммирования: DL — отметка планировки; NL — отметка поверхности

природного рельефа; FL — отметка подошвы фундамента; ВС — нижняя

граница сжимаемой толщи; Нс — сжимаемая толща

Таким образом, метод послойного суммирования в основном

используется при расчете небольших по размерам фундаментов зданий и

сооружений и при отсутствии в основании пластов очень плотных

малосжимаемых грунтов.

13. Расчет осадки фундаментов методом

эквивалентного слоя грунта.

Метод суммирования, как показывают приведенные выше примеры,

громоздок. Кроме того, он не является точным, так как основан на ряде

ранее отмеченных допущений. Во многих случаях расчет осадки

фундаментов может быть произведен по более простому методу

эквивалентного слоя. Основные допущения рассматриваемого метода

при мощном слое однородного грунта: 1) однородный грунт имеет

бесконечное распространение и пределах полупространства; 2)

деформации в пределах полупространства пропорциональны

напряжениям, т. е. полупространства линейно деформируемо; 3)

деформации полупространства устанавливаются методами теории

упругости. Из теории упругости известно, что осадка поверхности

линейно деформируемого полупространства может быть найдена по

формуле:

где ω — коэффициент осадки, зависящий от формы площади

загружения, жесткости фундамента и места расположения точки, в

которой определяется осадка; рд — интенсивность приложенного

давления, деформирующего рассматриваемое полупространство (грунты

основания), в кГ/см2; b — ширина площади загружения в см; Е —

модуль общей деформации грунта в кГ/см2; μ — коэффициент бокового

расширения грунта основания. Эта формула учитывает ограниченное

боковое расширение грунтов основания и деформации их под действием

всех компонентов напряжений.

14. Теория предельного напряженного состояния.

При действии внешних сил материал конструкции может находиться в

различных механических состояниях. При невысоких уровнях

напряжений материал пребывает в упругом состоянии. При

значительных напряжениях в материале обнаруживаются заметные

остаточные деформации и он переходит в пластическое состояние.

Затем, при дальнейшем увеличении внешних сил происходит

образование местных трещин, и наступает его разрушение.

Механическое состояние материала в точке зависит в первую очередь от

напряженного состояния в ней. С целью определения прочности

материалов вводится понятие предельное напряженное состояние.

Для пластичного материала предельным обычно считается, напряженное

состояние, которое соответствует возникновению заметных остаточных

деформаций, а для хрупкого - такое, при котором начинается

разрушение материала.

Для выполнения расчетов на прочность вводятся понятия

коэффициента запаса прочности и эффективное напряжение.

Коэффициент запаса при данном напряженном состоянии это число,

показывающее во сколько раз следует одновременно увеличить все

компоненты тензора напряжений, чтобы оно стало предельным.

Эквивалентное напряжение sЭКВ - это такое напряжение, которое

следует создать в растянутом образце, чтобы его напряженное состояние

было равно опасно с заданным.

Для пластичных материалов критерием наступления предельного

состояния принимается состояние, при котором максимальные

касательные напряжения достигают некоторого предельного значения:

sЭКВ = 2 tmax = s1 - s3 . (10.24)

Гипотеза максимальных касательных напряжений, приемлемая для

пластичных материалов, обнаруживает заметные погрешности для

материалов, имеющих различные механические характеристики при

сжатии и растяжении.

В таких случаях применяется энергетическая гипотеза, согласно

которой предельное состояние в точке наступает тогда, когда выражение

принимает некоторое заранее заданное значение. Это предельное

значение для UОФ определяется следующим образом. Для простого

растяжения выражение (10.25) принимает вид:

В сложном напряженном состоянии UОФ принимает значение

. (10.26)

При совместном рассмотрении (10.25) и (10.26) получим:

sЭКВ

или

sЭКВ

15. Устойчивость грунта в откосах .

При разработке грунта, устройстве насыпей (дамбы, земляные

плотины, дорожное полотно и т.д.) и выемок (котлованы, траншеи,

каналы и т.п.) и в ряде других случаев возникает необходимость в

устройстве откосов.

Откосом называется искусственно созданная поверхность,

ограничивающая природный грунтовый массив, выемку или насыпь.

Откосы нередко подвержены деформированию в виде обрушений

(рис. 9.1, а), оползней (см. рис. 91,б, в, г), осыпаний и оплываний

(см. рис. 9.1, д).

Обрушения имеют место при потере массивом грунта опоры у

подножия откоса. Оползни и оползания характеризуются

перемещением некоторого объема грунта. Осыпание происходит

при превышении силами сдвига сопротивления несвязного грунта

на незакрепленной поверхности. Оплыванием (сплывом) называется

постепенная деформация нижней части обводненного откоса или

склона без образования четких поверхностей скольжения.

Основными причинами потери устойчивости откосов являются:

устройство недопустимо крутого откоса;

устранение естественной опоры массива грунта из-за разработки

траншей, котлованов, подмыва откосов и т.д.;

увеличение внешней нагрузки на откос, например, возведение

сооружений или складирование материалов на откосе или вблизи

него;

снижение сцепления и трения грунта при его увлажнении, что

возможно при повышении уровня подземных вод;

неправильное назначение расчетных характеристик прочности

грунта;

влияние взвешивающего действия воды на грунты в основании;

динамические воздействия (движение транспорта, забивка свай и

т.п.), проявление гидродинамического давления и сейсмических сил.

Нарушение устойчивости откосов часто является результатом

нескольких причин, поэтому при изысканиях и проектировании

необходимо оценивать вероятные изменения условий

существования грунтов в откосах в течение всего периода их

эксплуатации.

Рис. 9.1. Характерные виды деформаций откосов: а — обрушение; б

— сползание; в — оползень; г — оползень с выпором; д —

оплывание; 1 — плоскость обрушения; 2 — плоскость скольжения;

3 — трещина растяжения; 4 — выпор грунта; 5 — слабый прослоек;

6,7—установившийся и первоначальный уровни воды; 8 —

поверхность оплывания; 9 — кривые депрессии

Различают три основных типа разрушения откоса (рис. 9.2):

разрушение передней части откоса (см. рис. 9.2,а). Для крутых

склонов (α > 60°) характерно сползание с разрушением передней

части откоса. Такое разрушение чаще всего возникает в вязких

грунтах, обладающих адгезионной способностью и углом

внутреннего трения;

разрушение нижней части откоса (см. рис. 9.2,6). На сравнительно

пологих откосах разрушение происходит таким образом, что

поверхность

скольжения соприкасается с глубоко расположенным твердым

слоем. Такой тип разрушения чаще всего возникает в слабых

глинистых грунтах, когда твердый слой расположен глубоко;

разрушение внутреннего участка откоса (см. рис. 9.2,в). Разрушение

происходит таким образом, что край поверхности скольжения

проходит выше передней части откоса. Такое разрушение также

возникает в глинистых грунтах, когда твердый сдой находится

сравнительно неглубоко.

Таким образом, основными причинами нарушения устойчивости

земляных масс являются эрозионные процессы и нарушение

равновесия. Эрозионные процессы в механике грунтов не

рассматриваются, так как они более подробно рассмотрены в

инженерной геологии.

Рис. 9.2. Типы разрушения откосов: а — разрушение передней части

откоса; б — разрушение нижней части откоса; в — разрушение

внутреннего участка откоса

Методы расчета устойчивости откосов

Основными элементами открытой разработки карьера, котлована

или траншей без крепления откосов является высота Н и ширина l

уступа, его форма, крутизна и угол естественного откоса?α (рис. 9.3).

Обрушение уступа происходит чаще всего по линии ВС,

расположенной под углом θ к горизонту. Объем ABC называется

призмой обрушения. Призма обрушения удерживается в равновесии

силами трения, приложенными в плоскости сдвига.

Нарушение устойчивости земляных масс часто сопровождается

значительными разрушениями мостов, дорог, каналов, зданий и

сооружений, расположенных на оползающих массивах. В результате

нарушения прочности (устойчивости природного склона или

искусственного откоса) формируются характерные элементы

оползня (рис. 9.4).

Устойчивость откосов анализируется с помощью теории

предельного равновесия или путем рассмотрения призмы

обрушения или сползания по потенциальной поверхности

скольжения как твердого тела.

Рис. 9.3. Схема откоса грунта: 1 — откос; 2 — линия скольжения;

3 — линия, соответствующая углу внутреннего трения; 4 —

возможное очертание откоса при обрушении; 5 — призма

обрушения массива грунта

Рис. 9.4. Элементы оползня

1 - поверхность скольжения; 2 - тело оползня; 3 - стенка срыва; 4

- положение склона до оползневого смещения; 5 - коренные

породы склона

Устойчивость откоса в основном зависит от его высоты и вида

грунта. Для установления некоторых понятий рассмотрим две

элементарные задачи:

устойчивость откоса идеально сыпучего грунта;

устойчивость откоса идеально связного массива грунта.

Устойчивость откоса идеально сыпучего грунта

Рассмотрим в первом случае устойчивость частиц идеально

сыпучего грунта, слагающего откос. Для этого составим

уравнение равновесия твердой частицы М, которая лежит на

поверхности откоса (рис. 9.5,а). Разложим вес этой частицы F на

две составляющие: нормальную N к поверхности откоса АВ и

касательную Т к ней. При этом сила Т стремится сдвинуть

частицу М к подножию откоса, но ей будет препятствовать

противодействующая сила Т', которая пропорциональна

нормальному давлению.

Устойчивость откоса идеально связного массива грунта

Рассмотрим устойчивость откоса АД высотой Нk для связного

грунта (рис. 9.5,6). Нарушение равновесия при некоторой

предельной высоте произойдет по плоской поверхности

скольжения ВД, наклоненной под углом?θ к горизонту, так как

наименьшей площадью такой поверхности между точками В и Д

будет обладать плоскость ВД. По всей этой плоскости будут

действовать силы удельного сцепления С.

Метод круглоцилиндрических поверхностей скольжения

Реальные грунты, как правило, обладают не только сцеплением,

но и трением. В связи с этим проблема устойчивости откосов

становится значительно сложнее, чем в рассмотренных случаях.

Поэтому на практике для решения задач в строгой постановке,

большое распространение получил метод круглоцилиндрических

поверхностей скольжения.

16. Давление грунта на подпорную стену.

Основные понятия и допущения

Давление грунта?на ограждающую поверхность зависит от

многих факторов:

способа и последовательности засыпки грунта;

естественного и искусственного трамбования;

физико-механических свойств грунта;

случайных или систематических сотрясений грунта;

осадок и перемещений стенки под действием собственного веса,

давления грунта;

типа сопряженных сооружений.

Все это значительно осложняет задачу определения давления

грунта. Существуют теории определения давления грунта,

использующие предпосылки, позволяющие с разной степенью

точности выполнять решения задачи. Отметим, что решение этой

задачи выполняется в плоской постановке.

Теория Кулона, предложенная в 1776 г., основывается на

рассмотрении предельного равновесия призмы грунта,

Ограниченной прямолинейными плоскостями обрушения

(выпирания). Более строгое решение о предельном равновесии

показывает, что действительное очертание этих поверхностей

скольжения является криволинейным. Однако величины

активного давления грунта на вертикальные или близкие к

вертикальным, жесткие, гладкие и шероховатые стенки,

определенные по Кулону и по точной методике,различаются

между собой на 2—3 % что, несомненно, можно считать

удовлетворительным результатом с инженерной точки зрения.

Пассивное давление грунта весьма существенно зависит от

трения грунта о стенку, которое в реальных условиях всегда

имеет место. Учет трения грунта о стенку с использованием

зависимостей, вытекающих из теории Кулона, дает при φ = 15—

20° существенную погрешность в сторону преувеличения по

сравнению с имеющимся решением. Более точные результаты

дает теория, предложенная СВ. Соколовским, построенная на

основе общей теории предельного напряженного состояния

сыпучей среды. Существуют различные интерпретации этой

теории, в том числе и хорошо известная графическая трактовка

С.С. Галушкевича.

В большинстве инженерных расчетов используются результаты,

полученные на основании теории Кулона; в тех случаях, когда

результаты следует уточнить, используются поправочные

коэффициенты, вводимые на основании точных решений и

экспериментальных данных. Различают следующие виды

бокового давления грунта:

давление покоя?(Eа), называемое также естественным

(натуральное), действующее в том случае, когда стена

(ограждающая поверхность) неподвижна или относительные

перемещения грунта и конструкции малы (рис. 10.7);

активное давление ? (Eа) возникающее при значительных

перемещениях конструкции в направлении давления и

образования плоскостей скольжения в грунте, соответствующих

его предельному равновесию (рис. 10.8). АБС — основание

призмы обрушения, высота призмы — 1 м;

пассивное давление?(Ер), появляющееся при значительных

перемещениях конструкции в направлении, противоположном

направлению давления и сопровождающееся началом «выпора

грунта» (рис. 10.9). АБС— основание призмы выпирания, высота

призмы —1м;

дополнительное реактивное давление (Еr), которое образуется

при движении конструкции в сторону грунта (в направлении,

противоположном давлению), но не вызывает «выпора грунта».

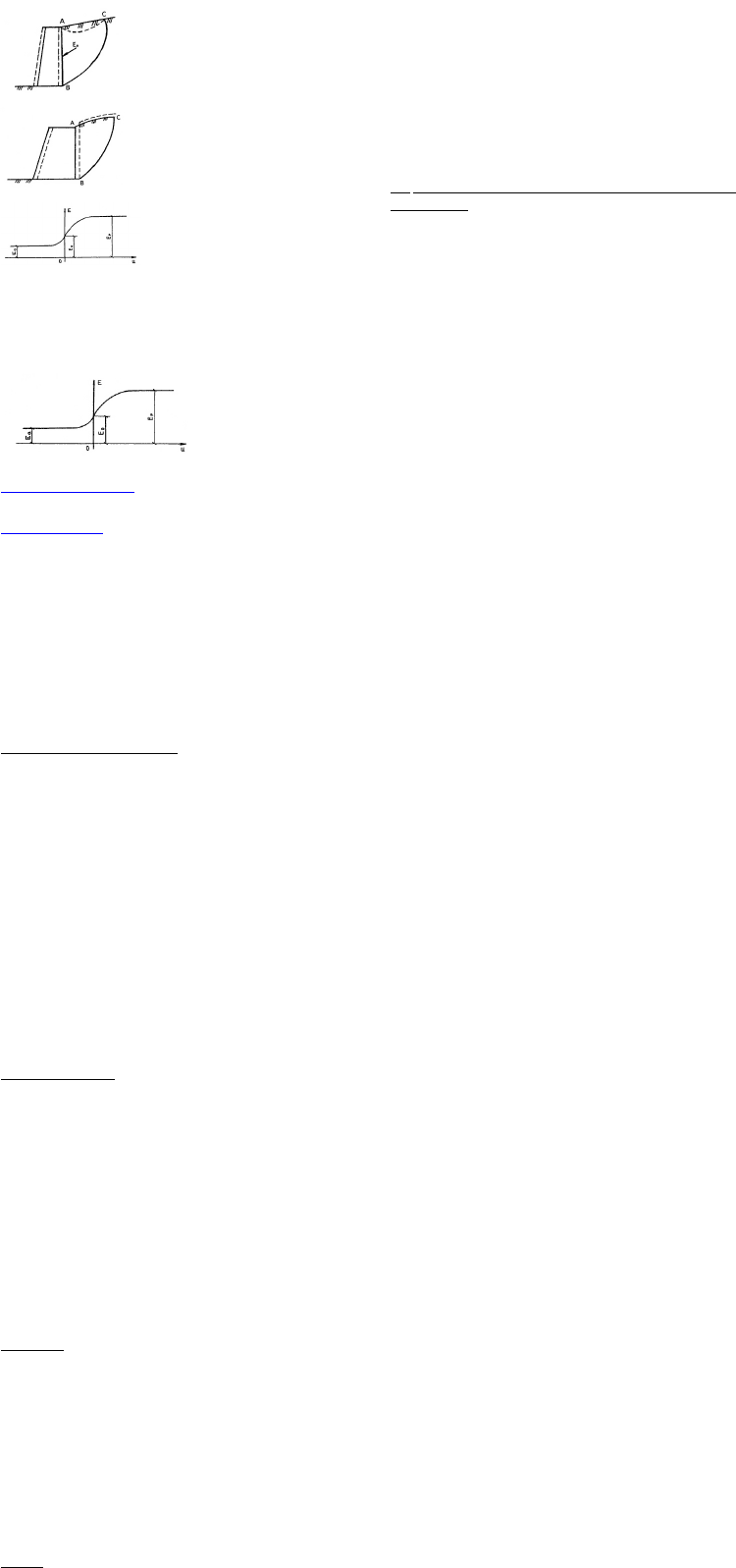
Рис. 10.7.?Схема к понятию давления покоя

Рис. 10.8.?Схема к понятию активного давления

Рис. 10.9.?Схема к понятию пассивного давления

Наибольшей из этих нагрузок (для одного и того же сооружения)

является пассивное давление, наименьшей — активное.

Соотношение между рассмотренными силами выглядит так:

?????Ea?< Eo < Er < Ep?????????????(10.1)

Изменение?давления грунта?в зависимости от перемещения стены и

представлено на?рис. 10.10.

Рис. 10.10.?Схема изменения давления грунта на подпорную стенку в

зависимости от ее перемещения

Активное давление грунта?вводится в качестве внешней нагрузки в

расчетах на устойчивость сооружений на сдвиг и прочность гибких

конструкций.

Пассивное давление?учитывается как предельная реактивная сила при

устойчивости и прочности сооружений, для которых горизонтальные

перемещения являются допустимыми.

Боковое давление грунта в состоянии покоя принимают во внимание в

том случае, когда устанавливают прочность уголковых и контрфорсных

подпорных стен, массивных стен камер шлюзов, доков и т.п.

Для расчета?подпорной стенки?необходимо знать полное давление на

любой участок, считая от поверхности земли. Рассматривая бесконечно

длинную стенку с одинаковыми условиями по ее длине, приводим

задачу к плоской. В этом случае рассматривается подпорная стенка

протяженностью 1 м. Давление грунта, приходящееся на единицу

высоты стенки шириной 1 м, называется интенсивностью давления,

которая считается распределенной по высоте стенки по линейному

закону.

17. Армирование грунтов

Укрепление откосов, насыпей и оврагов необходимо для

предотвращения водной и ветровой эрозии. С помощью армирующих

материалов легко решаются такие задачи, как укрепление слабых

оснований земляного полотна, усиление дорожной одежды, возведение

насыпей с откосами повышенной крутизны, строительство

армогрунтовых подпорных стен.

Армирование грунтов и грунтовых насыпей представляет собой

введение в грунтовые конструкции специальных элементов, которые

позволяют увеличить механические свойства грунта. Армирующие

элементы, работая в контакте с грунтом, перераспределяют нагрузку

между участками конструкции, обеспечивая передачу напряжений с

перегруженных зон на соседние менее загруженные участки. Такие

элементы могут быть изготовлены из различных материалов: метал,

железобетон структуры из стеклянных или полимерных волокон и т.д.

Наиболее эффективными и экономически выгодными для армирования

грунтов являются геосинтетические материалы, обладающие высокой

прочностью, устойчивостью к низким температурам и агрессивным

средам, неподверженностью коррозии и гниению, низкой ползучестью

(старением).

Одним из наиболее простых решений задачи укрепления грунтов

является геотекстиль, который представляет собой нетканое полотно из

синтетических полимерных волокон. Главной функцией геотекстиля

является укрепление грунта. Хорошая водопроницаемость этого полотна

позволяет свободно пропускать воду, однако не допускать вымывание

грунтов. Геотекстиль получил широкое применение при создании

ландшафта на слабых и техногенных грунтах, строительстве и

возведении гидротехнических сооружений, автомобильных и железных

дорог, аэродромов, туннелей, а также используется для предотвращения

эрозии почвы.

Наиболее распространенным материалом при укреплении склонов и

грунтов является применение геотекстиля дорнит. Дорнит представляет

собой иглопробивное полотно, которое хорошо пропускает воду,

осуществляя ее фильтрацию, и препятствует смешиванию слоёв грунта

при устройстве дорожного полотна или фундаментов Применение

геотекстильного полотна как материала для защиты и укрепления грунта

дало возможность строить дороги, выдерживающие довольно высокие

нагрузки, даже на слабом основании. Геоткань дорнит может

применяться как самостоятельно, так и совместно с георешётками,

которые являются не менее эффективным способом укрепления грунта.

Георешетка представляет собой гибкую ячеистую конструкцию из

пластиковых лент, скрепленных между собой сварными швами.

Георешетка применяется при организации противоэрозионной защиты

насыпей и откосов повышенной крутизны, неизбежной при

строительстве железнодорожных путей, автодорог, мостов, тоннелей,

пешеходных переходов через магистрали. Этот материал незаменим и

для укрепления прибрежных зон водоемов , в которых грунт особенно

сильно подвержен водной эрозии. Основными достоинствами при

укреплении ОТК Ёосов георешеткой является его высокая

устойчивость к пресной и соленой воде, грунтовой среде и

ультрафиолетовому излучению, что позволяет продлить срок службы

конструкции. В транспортном и гидротехническом строительстве

применение георешетки повышает надежность дорог и водоемов, что

уменьшает затраты на дополнительное обслуживание обслуживания зон

с нестабильной почвой.

Геосетка представляет собой геосинтетический материал, широко

применяемый для армирования и стабилизации строительных

конструкций. Эффективность применения материала геосетки

обеспечивается водостойкостью и долговечностью геосинтетика.

Этот материал устойчив к воздействию химических соединений и

ультрафиолета, не подвержен гниению и экологически безопасен.

На сегодняшний день геотекстиль «Стабитекс» является наиболее

эффективным геосинтетическим материалом, который применяется

для армирования слабых оснований при строительстве

автомобильных и железных дорог. «Стабитекс» представляет собой

геоткань, которая обладает высокой прочностью на растяжение,

изготавливается из полиамида, поэтому она может выдерживать

большие растягивающие нагрузки при незначительном удлинении.

18. Реологические свойства грунта: ползучесть и

релаксация

Характер сопротивления грунтов внешним силам зависит от

скорости приложения к ним этих сил. При быстром возрастании

нагрузки сопротивление грунта будет наибольшим и в нем будут

преобладать упругие деформации, при медленном возрастании

внешних сил — сопротивление грунта будет меньшим, и он будет

проявлять свойства ползучести и текучести.

Степень проявления упругости или ползучести в грунте зависит от

отношения времени действия силы к так называемому времени

релаксации, под которым понимается такой промежуток времени, в

течение которого напряжение уменьшается на определенную

величину, например, в е раз (е = 2,71).

Время релаксации различно у разных тел. Для скальных грунтов оно

измеряется сотнями и тысячами лет, для стекла около ста лет, а для

воды — 10-11 сек. Если продолжительность действия сил на грунт

меньше периода релаксации, то будут развиваться в основном

упругие деформации. Если же время действия силы на грунт

превышает время релаксации, то в грунте возникают необратимые

деформации ползучести и течения. Иными словами, в зависимости

от отношения времени действия силы ко времени релаксации тело

будет вести себя или как твердое, или как жидкое. Период

релаксации является основной константой, объединяющей свойства

твердых и жидких тел.

В современной физико-химической механике деление на жидко-

образные и твердообразные тела производится на основе картины

развития скорости деформации сдвига от величины действующего

сдвигающего давления.

Для жидкости при действии сколько угодно малых напряжений за

время, большее периода релаксации, устанавливается стационарное

течение с постоянной вязкостью, не изменяющейся при возрастании

напряжений. Для структурированных жидкостей (суспензий,

высокодисперсных и высоковлажных илов, сапропелей) вязкость

уже зависит от действующего касательного напряжения и поэтому

называется эффективной.

Для твердообразных тел, к которым относятся дисперсные и

скальные грунты, характерно наличие предельного напряжения

сдвига, называемого пределом текучести и совпадающего с

пределом упругости.

Для твердообразных тел говорят о пластической вязкости.

Н. Ф. Шведов (1889), а затем Бингам (1916) показали, что

пластические тела характеризуются двумя параметрами: пределом

текучести тел и пластической вязкостью.

Физический механизм ползучести очень сложен и зависит от

большого числа факторов. В кристаллах ползучесть обусловлена

движением дефектов структуры, двойникованием, трансляцией,

диффузией; в поликристаллических телах и дисперсных глинистых

грунтах, которые ползут при меньших давлениях, чем кристаллы, —

квазивязким скольжением частиц относительно друг друга,

переориентацией частиц в направлении, нормальном

результирующему напряжению, и развитием микротрещин.

Кинетика ползучести зависит от давления и температуры и

осложняется различными структурными превращениями —

уплотнением и упрочнением грунта на стадии затухающей

ползучести и дилатансным разупрочнением на стадии течения.

Для составления прогноза ползучести сооружений необходимо

знание двух величин — порога ползучести и эффективного

коэффициента вязкости грунта и его изменения во времени. Порог

ползучести (по Н. Н. Маслову) представляет собой такое

касательное напряжение, при котором и выше которого деформация

ползучести, имевшая до этого по своей величине и скорости

практически пренебрегаемый характер, резко интенсифицируется.

Порог ползучести грунтов зависит от структуры и состава грунта, от

температуры и давления и скорости действия давления. Для

плотных пород порог ползучести выше, чем для малоуплотненных.

«Порог ползучести» определяется по данным длительных опытов на

ползучесть идентичных образцов грунта, испытываемого при

различных значениях касательного напряжения.

Ж. С. Ержанов (1964) отмечает, что скальные грунты (алевролиты,

аргиллиты, песчаники, известняки) в условиях изгиба при

нагрузках, не превышающих ~70% от разрушающих, четко

обнаруживают свойство ползучести. Следовательно, порог

ползучести у этих пород может достигать нескольких десятков

кГ/см2. Из рассмотренных им пород специфическим поведением

при ползучести обладали известняки, ползучесть которых затухала в

10—20 раз быстрее, чем у других пород. Такое поведение

известняка, по-видимому, можно объяснить высоким углом

внутреннего трения и высокой вязкостью, присущих кальциту,

основному минералу, слагающему известняки.

Эффективная вязкость грунтов характеризует сопротивление их

течению под действием внешних сил. Количественно вязкость

определяется величиной касательной силы, которая должна быть

приложена в единице площади сдвигаемого слоя, чтобы поддержать

в нем ламинарное течение с постоянной скоростью относительного

сдвига, равной единице.

Факторы, определяющие вязкость грунтов. Вязкость грунтов

зависит от их структуры и текстуры, химико-минералогического

состава, от температуры и величины касательных напряжений.

Коэффициент вязкости для разных грунтов изменяется в очень

широких пределах: от 102—104 пз для илов с нарушенной

структурой до 1022 пз для известняка. С увеличением плотности

грунтов их вязкость, а также порог ползучести возрастают.

Нарушение структурных связей в глине путем ее перемятая

приводит к существенному уменьшению вязкости. Отношение

наибольшей вязкости к наименьшей возрастает от менее

дисперсных грунтов (суглинок лёссовидный, глина кембрийская)

к более дисперсным (хвалынская глина).

С увеличением интенсивности касательных напряжений вязкость

грунтов уменьшается, изменяясь от наибольшей вязкости по,

характерной для практически неразрушенной структуры, до

наименьшей вязкости, отвечающей структуре в состоянии

максимального нарушения связей между частицами.

Зависимость вязкости скальных грунтов от касательного

напряжения М. В. Гзовский аппроксимирует логарифмической

зависимостью.

М. В. Гзовский (1963) по величине вязкости горных пород в

природных условиях выделяет:

наименее вязкие породы (тощие глины, соли, гипсы,

тонкослоистые алевролито-глинистые толщи);

слабовязкие породы (тонкослоистые известняково-мергелистые,

песчано-глинистые, флишевые толщи);

сильно вязкие породы (слабо слоистые песчаниковые,

конгломератовые, карбонатные, вулканогенные, в прошлом

сильно дислоцированные и слабо метаморфизованные песчано-

глинистые толщи);

наиболее вязкие породы (граниты, гнейсы, кристаллические

сланцы);

Таким образом, петрографический состав является основным

фактором, который определяет вязкость монолитных пород.

Глины, соли и мергели обусловливают относительно низкую

вязкость грунтов, так как, присутствуя в виде прослоев, они

снижают вязкость песчаных и известняковых толщ и

способствуют их оползанию на склонах. Примером такого

смещения являются деформации Дзора ГЭС (Армения),

описанного Г. М. Ломизе (1945). Сооружение стало с некоторого

момента времени обнаруживать осевое сжатие в результате

давления толщи андезито-дацитов, сползавшей по слою

глинистых туфов, кровля которых была наклонена к горизонту

под углом порядка 8—9°. Геодезические наблюдения установили,

что скорость смещения толщи в направлении ГЭС измерялась

величиной 2—3 см/год.

Вязкость грунтов, так же как и жидкостей, зависит от

температуры. Однако исследования вязкости грунтов в диапазоне

температур, представляющих интерес для инженерной геологии

(примерно от —40 до +80° С), не проводились и данных об

изменении вязкости грунтов от температуры практически нет.

Расчеты, выполненные по данным изучения ползучести глин в

недренированных условиях при разных температурах, показали,

что для иллита увеличение температуры от 20 до 26°С привело к

уменьшению вязкости от 20•1012 до 0,7•1012 пз, т. е. почти в 30

раз.