Шпоры - Электропривод
Подождите немного. Документ загружается.

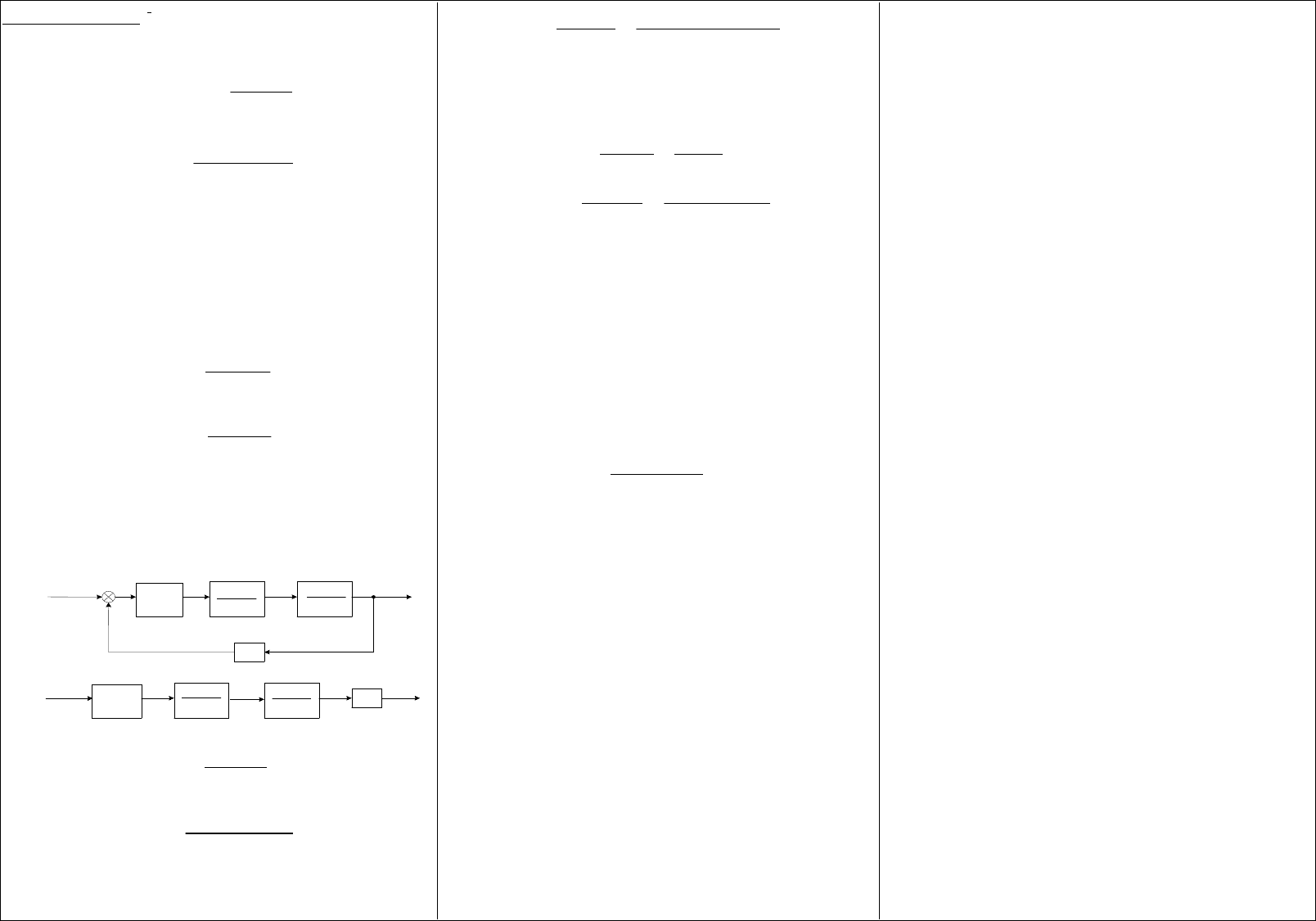
В этих выражениях коэффициент а определяет быстродействие контура регулирования и называется
коэффициентом демпфирования. В конечном итоге все контуры регулирования можно представить
эквивалентным инерционным звеном второго порядка с передаточной функцией (7.24).
С учетом вышепринятого допущения структурная схема любого контура системы подчиненного
регулирования может быть представлена в виде приведенном на рис. … . Согласно этой структурной
схеме передаточная функция разомкнутого контура запишется в следующем виде
окреграз
W
ра
рWрW
1
1
)()(
. (7.25)
Тогда, из условия равенства правых частей (7.24) и (7.25) получим выражение для определения
передаточной функции регулятора
)(
1
)(
ррWа
рW
ок
рег
. (7.26)
7.3. Синтез системы подчиненного регулирования.
Синтез системы подчиненного регулирования заключается в последовательной оптимизации
соподчиненных замкнутых контуров регулирования, начиная с первого внутреннего и кончая
основным внешним. При синтезе системы по заданной структуре и параметрам подобъектов
регулирования определяется структура и параметры соответствующих регуляторов.
Под оптимизацией контура регулирования понимается придание контуру таких статических и
динамических свойств при которых он удовлетворяет требованиям, определяются принятым
критериям оптимальности. При этом необходимо отметить, что оптимизация всех соподчиненных
контуров в многоконтурной системе осуществляется по единой методике и выполняется
последовательно начиная с первого внутреннего конура и кончая основным внешним контуром.
Рассмотрим методику синтеза на примере одного контура подчиненного регулирования с учетом
определенного критерия оптимальности. Структурная схема контура подчиненного регулирования
приведены на рис. 7.3а, в которой объект регулирования представлен звеном с малой
некомпенсируемой постоянной и единичным передаточным коэффициентом
1
1
)(
рТ
рW
НК
(7.27)
и объектом компенсации
1
)(
0
0
рТ
К
рW
ОК
. (7.28)
При этом имеется ввиду, что обратная связь в контуре не единичная.
Для определения передаточной функции регулятора по выше изложенной методике исходную
структурную схему необходимо представить в виде разомкнутой структурной схемы с выходом по
сигналу обратной связи, как это показано на рис. 7.3б.
Исходя из структурной схемы, некомпенсируемая постоянная времени равна
Т
,
Х
вх
(р)
Х
вых
(р)
)р(W
рег
1рТ
1
1рТ
к
0
0
ос
к
Х
вх
(р)
ос
к
Х
вых
(р)
)р(W
рег
1рТ
1
1рТ
к
0
0
а)
б)
Рис. 7.3. Структурные схемы контура регулирования: а – замкнутого; б - разомкнутого.
а передаточная функция расчетного объекта компенсации запишется в следующем виде:
1
)(
рТ
КК
рW
о
око
ок
. (7.29)
Подставив эти данные в ( ) получим передаточную функцию регулятора в следующем виде
КосрКаТ
рТ
рW
о
рег
1
)(
0
. (7.30)
Полученное выражение позволяет определить структуру регулятора, а для определения параметров
регулятора необходимо знать значение коэффициента демпфирования а.
Передаточная функция замкнутого контура, учитывая (7.30), с выходом по сигналу обратной связи
запишется в следующем виде
1
1
)(
)(
)(
22
раТраТрХ
рХ
рW
вх
ос
з
(7.31)
Из этого следует, что динамические свойства контура, при заданном значении некомпенсируемой
постоянной времени
Т
, зависят только от коэффициентов демпфирования. Он может быть
определен из условия обеспечения оптимального переходного процесса.
В системах подчиненного регулирования за оптимальный принимается переходный процесс в
идеальном фильтре, при котором достигается максимальное быстродействие, т.е. минимальное
время регулирования, при перерегулировании не превышающем 20%. Такой оптимум
динамического процесса называется техническим или модульным.
Применительно к этому оптимуму желаемая передаточная функция системы второго порядка
исходя из нормированной равна
14,1
1
)(
)(
)(
2
рррХ
рХ
рW
вс
ос
ж
. (7.32)
Тогда, из условия
)()( рWрW
жз
, (7.33)
получим следующие равенства
а
1
2
Т
; (7.34)
а
4,1
Т
, (7.35)
из которых следует, что
а=1,4
2
2 (7.36)
Таким образом, из условия принятого оптимума динамического процесса, получено конкретное
значение коэффициента демпфирования контура регулирования, в соответствии с которым
определяются параметры регулятора.
Далее необходимо отметить, что при оптимизации какого-либо внешнего контура по отношению к
одному или ряду внутренних контуров, в полиноме знаменателя передаточной функции не
учитываются члены высшего порядка от р, а учитывается лишь член первого порядка, т.е.
передаточная функция внутренних контуров равна
1
1
)(
2
рсаТ
рW
вн
, (7.37)
где с – целое число, зависящее от количества внутренних контуров
