Шпоры - Дискретный анализ
Подождите немного. Документ загружается.

Вопросы для подготовки к экзамену по дисциплине
«Дискретный анализ»
1. +Понятие множества, элементов множества,
подмножество, универсальное множество, пустое
множество.
Множество – неупорядоченная именованная
совокупность элементов, удовлетворяющая следующим
условиям:
каждый элемент совокупности уникален, т. е.
отличим от других;
для любого объекта существует возможность
установить, принадлежит ли он множеству или нет.
Принадлежность элемента а множеству А обозначается
аА
( происходит от греческой буквы ).
Элементы множества в математике принято заключать в
фигурные скобки {1, 2, 3, 4, 5, 6}.
Элементами множества могут быть объекты разной
природы и структуры. В частности, множества могут
сами быть элементами множеств. Примеры: множество
студентов одной группы; множество команд языка
программирования; множество групп студентов 2-го
курса и т.д. В последнем случае элементы (группы
студентов) сами являются множествами.
Число элементов множества А обозначается как А и
называется мощностью (размером, нормой, длиной и др.)
множества А. Вводится множество, не содержащее
элементов, обозначаемое символом и называемое
пустым множеством. Пустое множество может
встретиться в реальных задачах и не является
«изобретением» математиков. Так, например, может
оказаться, что множество студентов, получивших две
неудовлетворительные оценки, пусто (таких студентов
просто нет).
Для сокращения записи используется символ | вместо
слов «таких, что». В дальнейшем будем применять также
символы & для обозначения связки И, | для обозначения
связки ИЛИ, квантор общности a (для всех a) и квантор
существования a (существует a).
Множества А и В равны, что обозначается как А=В, если
(а А b В, а=b) ( b В aА, а=b).
Это условие лежит в основе методов проверки равенства
двух множеств.
Если заведомо выполняется только условие, записанное
в первой скобке определения равенства, то множество A
является частью множества В или его подмножеством,
что обозначается как А В.
Для множества A множество B называется дополнением
A, если в B включены те и только те элементы, которые
не принадлежат A (обозначается как B = ~A, В =A или B
=А). Эту операцию ещё называют НЕ, т.е. говорят B
равно НЕ А.
Предполагается, что дополнение происходит до
некоторого универсального множества (универсума),
определяемого предметной областью задачи.
Универсальное множество обозначается символом U.
Любое множество является подмножеством
универсального множества. Например, универсальным
множеством может быть множество студентов
факультета, и для него можно рассматривать множества
студентов конкретных групп, студентов, получающих
именные стипендии и т.п.
Под множеством понимают совокупность объектов
произвольной природы различимых по некоторому
признаку. Объекты, принадлежащие множеству,
называются его элементами. Элементы множества в
математике принято заключать в фигурные скобки {1, 2,
3, 4, 5, 6}.
Множества принято обозначать большими буквами
латинского алфавита
,...,, CBA
, а
элементы множеств малыми буквами
,...,, cba
. Если множество имеет конечное
число элементов, то его можно описывать, перечисляя
элементы в фигурных скобочках через запятую:
6,5,4,3,2,1A
,
xtrbaB ,,,,
,
где А – множество натуральных чисел 1,2,3,4,5 и 6, а В –
множество букв a,b,r,t и x.
В этом случае говорят, что, например, элемент 3
принадлежит множеству А (обозначается
A3
).
Если же объект не является элементом множества
(например, 10 для множества А), то говорят, что он не
принадлежит множеству (обозначается
A10
).
Множество также можно определять указанием свойства
элементов данного множества.
Пример 1.1.
0532
2
xxRxC
,
то есть множество С состоит из тех действительных
чисел x, которые удовлетворяют неравенству
0532
2
xx
.
Определение 1.1. Множество А называется
подмножеством множества В (обозначается
BA
), если каждый элемент множества А
является элементом множества В.
Пример 1.2.
Множество
7,5,3A
является
подмножеством множества
14,9,7,5,3,1B
, то есть
BA
.
Определение 1.2. Говорят, что множество А равно
множеству (обозначается А=В), если любой
Ax
, тогда и только тогда, когда
Bx
. Иначе говоря,
имеют место два включения:
BA
и
AB
.
Если
BA
и
BA
, то это записывают
BA
и говорят, что А есть собственное
подмножество множества В.
Определение 1.3. Пустым множеством (обозначается
) называется множество, которое не содержит
элементов.
Определение 1.4. Универсальным множеством E
называется множество, обладающее таким свойством,
что все рассматриваемые множества являются его
подмножествами.
2. +Операции над множествами и их семействами:
объединение, пересечение, дополнение, разность.
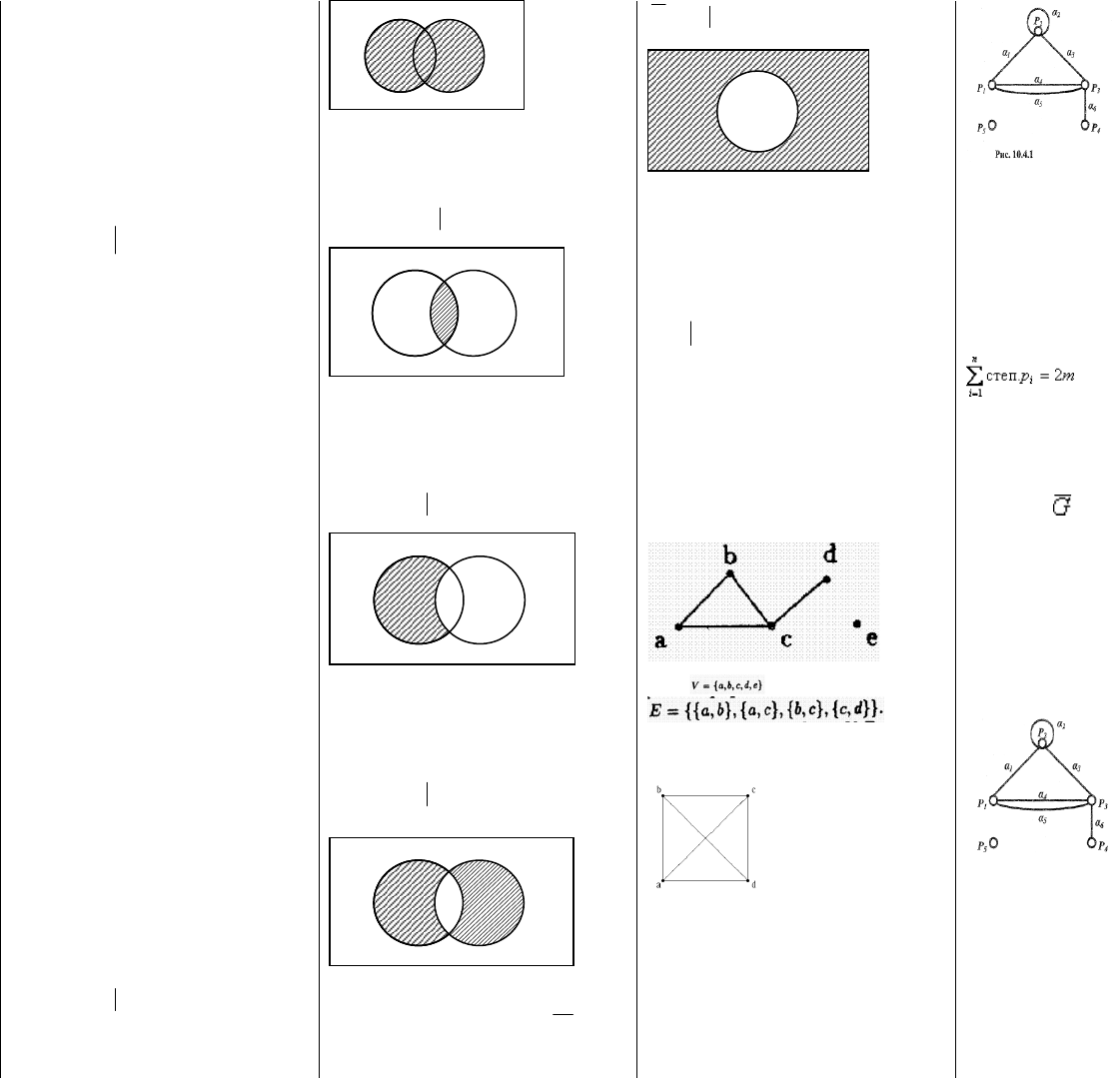
При изучении операций над множествами удобно
использовать диаграммы Эйлера. На них универсальное
множество изображается в виде прямоугольника, а
рассматриваемые множества в виде кружков,
расположенных внутри прямоугольника. Множество,
полученное после выполнения операций над
множествами, изображают заштрихованной областью.
Объединением множеств А и В (обозначается
BA
) называется множество, состоящее из всех
тех элементов, которые принадлежат хотя бы одному из
множеств A или B (рис. 2.1.). То есть:
BxилиAxxBA
.
Пересечением множеств А и В (обозначается
BA
) называется множество, состоящее из всех
тех и только тех элементов, которые принадлежат и А, и
В (рис. 2.2.). То есть:
BxAxxBA и
.
Разностью множеств А и В (обозначается
BA /
)
называется множество всех тех и только тех элементов
множества А, которые не содержатся во множестве В
(рис. 2.3.). То есть:
BxAxxBA и /
.
Симметрической разностью множеств А и В
(обозначается
BA
) называется множество всех
тех и только тех элементов, которые принадлежат либо
только А, либо только В (рис. 2.4.). То есть:
AxBxилиBxAxxBA и и
.
Дополнением множества А (обозначается
A
)
называется множество, состоящее из элементов, не
принадлежащих множеству А (рис. 2.5.). То есть:
AxxA
.
Для трех, четырех и более множеств операции
определяются аналогично. Так, например, для множеств
n
AAA ,...,,
21
их объединение:
i
n
n
i
i
Axчтоniтакоесуществуетx
AAAA
,1
...
21
1
3. + Понятие графа. Полный граф. Вершина, степень
вершины.
Граф (graph) G — множество вершин V и набор рёбер E.
G = G(V, E)
Простым графом называется упорядоченная пара G =
G(V, E),
где ‚V — непустое конечное множество (элементы V —
вершины графа);
Е — конечное множество неупорядоченных пар
различных элементов V (элементы E — ребра графа).
Графы удобно представлять рисунками, в которых
вершины изображаются точками, а ребра — линиями,
соединяющими соответствующие точки.
на рисунке изображен простой граф с множеством
вершин и множеством ребер
Полным называется граф, у которого каждые две
вершины соединены ребром. В полном графе любые две
вершины смежные. Полный граф с n вершинами
обозначают K
n
.
Вершины в графе могут отличаться друг от друга тем,
скольким ребрам они принадлежат.
Степенью вершины называется число ребер,
инцидентных ей. Вершина степени 1 называется висячей.
Вершина степени 0 называется изолированной. На рис.
10.4.1 степень вершины Р
1
равна трем, Р
4
—висячая
вершина, Р
5
—изолированная.
Количество ребер, выходящих из вершины, называется
ее степенью. Четная вершина - та, у которой это
количество четно, нечетная - та, у которой оно нечетно.
Вершина называется изолированной, если ее степень
равна 0, и висячей, если ее степень равна 1.
Имея даже общие представления о графе, иногда можно
судить о степенях его вершин. Так, степень каждой
вершины полного графа на единицу меньше числа его
вершин.
4. +Теорема о сумме степеней вершин графа.
Теорема о числе нечетных вершин графа.
Теорема 1: В графе G сумма степеней всех его вершин -
число п четное, равное удвоенному числу ребер графа:
, где п - число вершин графа, m —
число его ребер.
Теорема 2: Число нечетных вершин любого графа, т. е.
вершин, имеющих нечетную степень, четно.
Граф G называется полным, если любые две его
различные вершины соединены ребром, и он не
содержит параллельных ребер. Дополнением графа G
называется граф с теми же вершинами, что и граф G
и содержащий только те ребра, которые нужно добавить
к графу G чтобы получился полный граф. Граф G
называется плоским, если он может быть изображен на
плоскости так, что все пересечения ребер являются его
вершинами.
5. + Цикл. Путь. Длина пути. Связность графа.
Мост. Деревья, лес.
Путем в графе называется такая последовательность
ребер, ведущая от некоторой начальной вершины Р1 в
конечную вершину Рn, в которой каждые два соседних
ребра имеют общую вершину и никакое ребро не
встречается более одного раза. Например, в графе,
изображенном на рис.
последовательность ребер (а
1
, а
2
, а
3
, а
4
, а
5
, а
6
) образует
путь, ведущий от вершины Р
1
к вершине Р
4
.
Циклом называется путь, начальная и конечная
вершины которого совпадают. На рис. ребра (a
1
, a
3
, a
4
)
образуют цикл.
Цикл графа G называется простым, если он не проходит
ни через одну вершину G более одного раза.
Длиной пути или цикла называется число ребер этого
пути или цикла.
Граф G называется связным, если для любых двух его
вершин существует путь, их соединяющий. В противном
случае граф G называется несвязным.
Связный граф без циклов называется деревом.
Граф называется деревом, если
E
A
B
рис.2.1
.
E
A
B
рис.
2.2.
E
A
B
рис.
2.3.
E
A
B
рис.
2.4.
E
рис.
2.5.
A
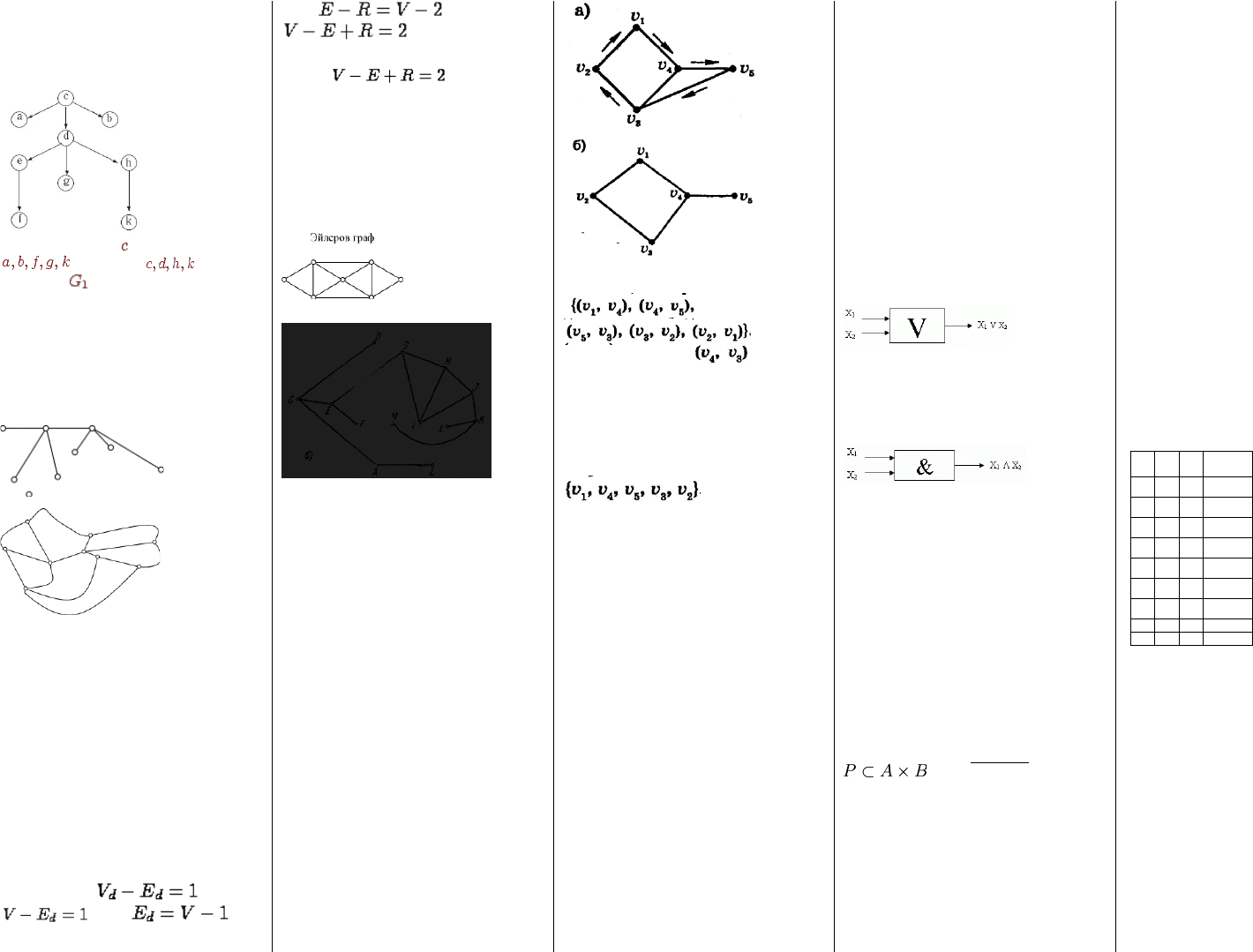
1. в нем есть одна вершина, в которую не входят ребра;
она называется корнем дерева;
2. в каждую из остальных вершин входит ровно по
одному ребру;
3. все вершины достижимы из корня.
Граф, являющийся объединением нескольких
непересекающихся деревьев, называется лесом.
В дереве на рис. вершина является корнем, вершины
- листья. Путь - одна из
ветвей дерева .
6. + Плоский граф. Формула Эйлера о числе ребер и
числе граней для плоского представления плоского
связного графа.
Плоский граф — это граф, нарисованный таким
образом, что его ребра не пересекаются. Говорят, что
граф допускает плоскую укладку, если его можно
нарисовать как плоский. Также плоские графы называют
планарными. Плоские графы — это простые циклы,
деревья, лес, а также граф, содержащий цикл, из вершин
которого "выходят" деревья
Формула Эйлера
Для всякого плоского представления связного плоского
графа без перегородок число вершин (V), число ребер (E)
и число граней с учетом бесконечной (R) связаны
соотношением V-E+R=2
Пусть граф G— связный, плоский граф без перегородок.
Определим значение алгебраической суммы V-E+R для
его произвольного плоского представления.
Преобразуем данный граф в дерево, содержащее все его
вершины. Для этого удалим некоторые ребра графа G,
разрывая поочередно все его простые циклы, причем так,
чтобы граф оставался связным и без перегородок.
Заметим, что при таком удалении одного ребра число
граней уменьшается на 1, так как при этом либо
пропадет один простой цикл, либо два простых цикла
преобразуются в один. Следовательно, значение
разности E-R при этом остается неизменным.
На рисунке ребра, которые мы удаляем, изображены
кривыми. В полученном дереве обозначим число вершин
—V
d
, число ребер —E
d
, число граней — R
d
. Справедливо
равенство. E-R= E
d
- R
d
В дереве одна грань, то есть E-R= E
d
- 1. Операция
удаления ребер из графа не меняет число его вершин, то
есть V=V
d
. B дереве . Отсюда
, то есть , а
потому или
.
Итак, доказано, что если в плоском представлении
связного графа без перегородок V вершин, E ребер и R
граней, то . Полученная
формула называется формулой Эйлера.
7. +Эйлеровы графы и Эйлеровы пути.
Эйлеровым называется цикл, проходящий по каждому
ребру графа ровно один раз.
Граф, имеющий эйлеров цикл, тоже будем называть
эйлеровым.
Связный граф является эйлеровым тогда и только тогда,
когда степени всех его вершин – чётные числа.
Эйлеровым путем в графе называется путь, содержащий
все ребра графа. Эйлеровым циклом в графе называется
цикл, содержащий все ребра графа.
8. + Лабиринты. Циклы.
Лабиринты, как известно, состоят из коридоров,
перекрестков, тупиков (любой участок можно проходить
по несколько раз), и маршруты в них могут быть
представлены графами, в которых ребра соответствуют
коридорам, а вершины — входам, выходам,
перекресткам и тупикам.
Задача о лабиринте в общем случае сводится к
построению алгоритма, позволяющего отыскать
маршрут в соответствующем графе от заданной вершины
v
a
до заданной вершины v
b
. Вершина v
a
может быть
входом или внутренней точкой лабиринта, из которой
нужно выбраться, вершина v
b
— выходом или тоже
внутренней точкой, в которую необходимо попасть.
Чтобы избежать бесконечного блуждания, необходимо
иметь возможность запоминать пройденный путь,
например, отмечать ребра графа, по которым уже
прошли, и направление пути.
Циклом в графе называется замкнутый путь, не
проходящий дважды через одну точку.
9. +Гамильтоновы графы, гамильтоновы пути и
циклы.
Граф называется гамильтоновым, если в нём имеется
цикл, содержащий каждую вершину этого графа. Сам
цикл также называется гамильтоновым.
Гамильтоновым называется цикл, проходящий по
каждой вершине графа ровно один раз.
Гамильтонов путь (или гамильтонова цепь) — путь
(цепь), содержащий каждую вершину графа ровно один
раз.
Гамильтонов путь, начальная и конечная вершины
которого совпадают, называется гамильтоновым
циклом. Гамильтонов цикл является простым основным
циклом.
На рис., направление одного из гамильтоновых циклов
отмечено стрелками. Соответствующий гамильтонов
цикл представлен последовательностью ребер
Можно заметить, что ребро в этом цикле не
используется.
Этот факт указывает на то, что в гамильтоновом цикле
могут участвовать не все ребра графа. Существенным в
цикле данного типа является наличие всех вершин графа.
В связи с этим в случаях, когда нет кратных ребер,
гамильтонов цикл записывают последовательностью
вершин. Так, в рассмотренном примере гамильтонов
цикл можно представить следующей
последовательностью вершин:
.
10. +Понятие алгебры логики, булевой алгебры.
История создания алгебры логики.
Алгебра логики - это математический аппарат, с
помощью которого записывают, вычисляют, упрощают и
преобразовывают логические высказывания.
Алгебра логики — раздел математической логики, в
котором изучаются логические операции над
высказываниями. Высказывания могут быть истинными
и ложными.
Булева алгебра - раздел математической логики,
изучающий высказывания и операции над ними.
Наиболее известными операциями булевой алгебры
являются: конъюнкция, дизъюнкция, импликация,
эквивалентность, отрицание.
История.
Логика - наука, изучающая методы доказательств и
опровержений, т.е. методы установления истинности или
ложности одних высказываний (утверждений) на
основе истинности или ложности других высказываний.
Математическая логика - это современная форма
логики , которая полностью опирается на формальные
математические методы. Основы логики как науки
были заложены великим древнегреческим учёным
Аристотелем (4 век до н.э.), а со средины 19 века
благодаря трудам англичанина Дж. Буля 1815 -1864),
шотландца А. де Моргана (1806 - 1871), немца Г.Фреге
(1848 - 1925), итальянца Дж. Пеано (1858 - 1932) и
других возникла математическая логика , которая
перевела на точный язык математики все прежние
достижения логики , дала мощный толчок её
дальнейшему развитию и существенно повысила уровень
строгости и доказательности математики в целом.
11. + Понятие высказывания. Операции над
высказываниями (дизъюнкция, конъюнкция,
отрицание).
Алгебра высказываний – раздел математической логики,
занимающийся
построением и преобразованием высказываний с
помощью логических опера-
ций, а также изучающий свойства и отношения между
ними.
При этом под высказываниями понимается всякое
предложение, относительно которого можно утверждать,
что оно истинно или ложно.
Приведем примеры высказываний:
1) Москва – столица России;
2) число 27 является простым;
3) Волга впадает в Каспийское море.
Высказывания 1 и 3 являются истинными. Высказывание
2 – ложным, потому что число 27 составное 27=3*3*3.
Дизъюнкция высказываний (V, ИЛИ, OR)
Это сложное высказывание истинно тогда, когда истинно
хотя бы одно высказывание, входящее в него.
Читается X
1
ИЛИ X
2
: Некоторое отличие от смысла
союза "или", принятого в русском языке: в данном
случае этот союз употребляется в смысле объединения, а
не разъединения.
Конъюнкция высказываний (&, И, AND).
Возьмем 2 высказывания:
А=<Киев – столица Украины>
В=<дважды два - четыре>
тогда сложное высказывание: А & В будет истинным,
так как истинны оба этих высказывания.
Функция конъюнкции истинна тогда, когда истинны
одновременно оба высказывания.
Отрицание высказываний (– над буквой, НЕ, NOT).
Отрицанием высказывания называется высказывание,
истинное только тогда, когда исходное высказывание
ложно.
12. + Унарные операции, бинарные операции, n-
арные операции.
В зависимости от количества операндов различают
одноместные (унарные), двуместные (бинарные) и
многоместные (n-арные) операции
Унарной операцией или одноместной операцией на
множестве M называется отображение множества в себя
M→M, которое каждому элементу множества M,
называемому операндом, ставит в соответствие
некоторый элемент того же множества, называемый
результатом.
Унарную операцию принято обозначать знаком
действия, который ставится перед или над операндом.
Например, для унарной операции «?» результат её
применения к элементу x записывается в виде - x.
Пусть A,B,C — тройка непустых множеств. Бинарной
операцией или двуместной операцией в паре A, B со
значениями в C называется отображение P→C, где
Если A = B = C, то действие называется внутренним,
если A = C или B = C— внешним. В частности, любое
внутреннее действие является внешним.
Бинарную операцию принято обозначать знаком
действия, который ставится между операндами
(инфиксная форма записи). Например, для произвольной
бинарной операции ○ результат её применения к двум
элементам x и y записывается в виде x○y
Это не значит, что не используются другие формы
записи бинарных операций. Существуют и другие виды
записи:
префикснаяn— x○y;
постфикснаяn — xy○.
n-арным (n-местным) отношением на множестве A
называется подмножество n-ой декартовой степени An
множества A.
Число n для n-арной операции f (n-арного отношения r)
называется арностью операции f (отношения r) и
обозначается n(f) (n(r)).
Арности отношений – это числа большие нуля.
Арности операций – это числа большие или равные
нулю. Операции арности 0 представляют собой функции
с областью определения, состоящей из одного элемента
(n-ки длины 0) и отождествляются со значением
функции
13. -Понятие набора. Понятие «значения функции на
данном наборе».
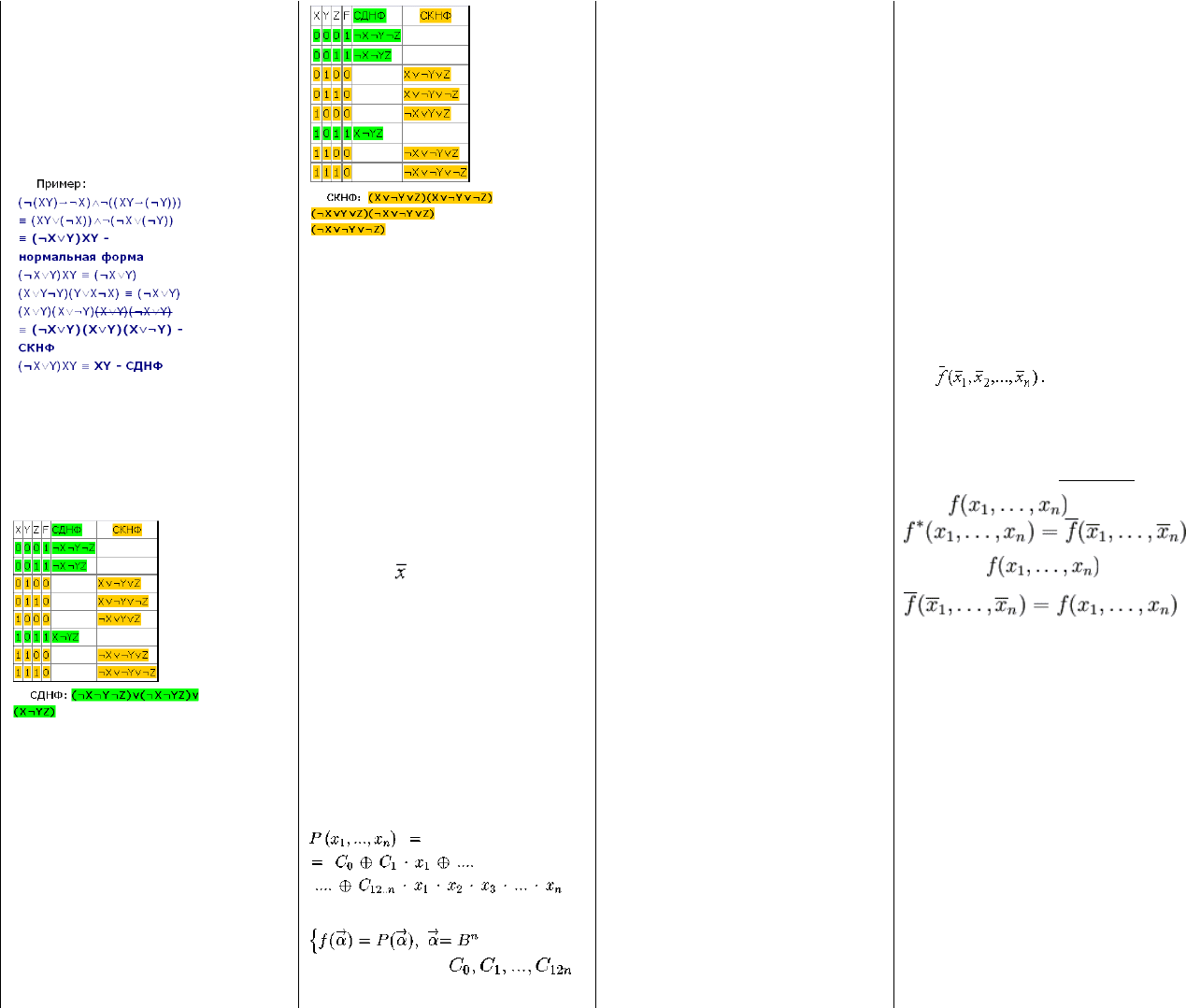
14. +Методика построения таблиц истинности
логических функций.
Логической ( булевой) функцией (или просто функцией)
n переменных y = f(x1, x2, …, xn) называется такая
функция, у которой все переменные и сама функция
могут принимать только два значения: 0 и 1.
Из определения логической функции следует, что
функция п переменных – это отображение Е
п
в Е,
которое можно задать непосредственно таблицей,
называемой таблицей истинности данной функции.
Например, функция трех переменных f(x,y,z)
может определяться
следующей таблицей
истинности.
x y z f(x,y,z
)
0 0 0 1
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 0
1 1 1 0
Это означает, что f(0,0,0) = 1, f(0,0,1) = 0, f(0,1,0) = 1 и
т.nд.
15. +Понятие дизъюнктивной нормальной формы
(ДНФ).
Формула D называется дизъюнктивной нормальной
формой (ДНФ), если она является дизъюнкцией
элементарных конъюнкций, т.е. имеет вид
D=K
1
vK
2
v…K
r
, где каждая формула
K
j
(j =1,...,r) - это элементарная конъюнкция. D
называется совершенной ДНФ, если в каждую из ее
конъюнкций K
j
входят все n переменных из X
Элементарной конъюнкцией называется конъюнкция
переменных высказываний и (или) их отрицаний.
Элементарной дизъюнкцией называется дизъюнкция
переменных высказываний и (или) их отрицаний.
16. +Понятие конъюнктивной нормальной формы
(КНФ).
формула C называется конъюнктивной нормальной
формой (КНФ), если она является конъюнкцией
элементарных дизъюнкций, т.е.
C=D
1
v D
2
v…v D
r
,
где каждая формула D
j
(j =1,...,r) - это элементарная
дизъюнкция. Она является совершенной КНФ, если в
каждую D
j
входят все n переменных из X
Элементарной конъюнкцией называется конъюнкция
переменных высказываний и (или) их отрицаний.
Элементарной дизъюнкцией называется дизъюнкция
переменных высказываний и (или) их отрицаний.
17. +Понятие совершенной дизъюнктивной
нормальной формы (СДНФ).
Определение 1.
Элементарная конъюнкция называется правильной,
если в неё каждая переменная входит не более одного
раза, включая её вхождение и под знаком отрицания.
Определение 2.
Элементарная конъюнкция называется полной
относительно переменных x,y,z ..., если в неё входит
каждая из этих переменных не менее одного раза,
включая и их вхождение под знаком отрицания.
Определение 3.
Совершенной дизъюнктивной нормальной формой
(СДНФ) относительно переменных x,y,z,... ,
называется дизъюнктивная нормальная форма, в которой
нет одинаковых элементарных конъюнкций и все
элементарные конъюнкции правильные и полные
относительно переменных x,y,z,... .
Т.е.:
1) Различны все члены конъюнкции ("множители");
2) Различны все члены каждой дизъюнкции
("слагаемые");
3) В каждой дизъюнкции нет одновременно переменной
и ее отрицания;
4) Каждая дизъюнкция содержит все переменные,
входящие в данную формулу или их отрицания.n
18. +Понятие совершенной конъюнктивной
нормальной формы (СКНФ).
Определение 1.
Элементарная дизъюнкция называется правильной,
если в неё каждая переменная входит не более одного
раза, включая её вхлждение и под знаком отрицания.
Определение 2.
Элементарная дизъюнкция называется полной
относительно переменных x,y,z ..., если в неё входит
каждая из этих переменных не менее одного раза,
включая и их вхождение под знаком отрицания.
Определение 3.
Совершенной конъюнктивной нормальной формой
(СКНФ) относительно переменных x,y,z,... ,
называется конъюнктивная нормальная форма, в которой
нет одинаковых элементарных дизъюнкций и все
элементарные дизъюнкции правильные и полные
относительно переменных x,y,z,... .
Т.е.:
1) Различны все члены дизъюнкции ("слагаемые");
2) Различны все члены каждой конъюнкции
("множители");
3) В каждой конъюнкции нет одновременно переменной
и ее отрицания;
4) Каждая конъюнкция содержит все переменные,
входящие в данную формулу или их отрицания.n
19. + Правила приведения произвольной формы
алгебры логики к СДНФ и СКНФ.
Приведение формулы к СДНФ с помощью
равносильных преобразований:
1) Привести формулу к нормальному виду (т.е.
избавиться от импликации, эквиваленции и отрицания
неэлементарных формул).
2) Из всех одинаковых членов дизъюнкции
("слагаемых") оставить только один.
3) Если в каком-то члене дизъюнкции ("слагаемом") не
хватает переменной X
i
, то "домножаем" его с на
(X
i
v¬X
i
), т.е. на 1 .
4) Раскрыть скобки и из всех одинаковых членов
дизъюнкции ("слагаемых") оставить только один.
Приведение формулы к СКНФ с помощью
равносильных преобразований:
1) Привести формулу к нормальному виду (т.е.
избавиться от импликации, эквиваленции и отрицания
неэлементарных формул).
2) Из всех одинаковых членов конъюнкции
("множителей") оставить только один.
3) Если в каком-то члене конъюнкции ("множителе") не
хватает переменной X
i
, то "прибавить" к нему
(X
i
Λ¬X
i
), т.е. 0 .
4) Раскрыть скобки и из всех одинаковых членов
конъюнкции ("множителей") оставить только один.
Пример:
20. +Методика построения СДНФ по таблице
истинности логической функции.
1) Выбрать из таблицы истинности те строки, в которых
значение формулы - "Истина" (1).
2) Для каждой выбранной строки составить конъюнкцию
переменных или их отрицаний так, чтобы эта
конъюнкция была истинной (для этого переменные,
которые в соответствующей строке имеют значение
"Ложь" (0) нужно взять с отрицанием, а переменные,
имеющие значение "Истина" - без отрицания).
3) Составить дизъюнкцию полученных конъюнкций.
21. +Методика построения СКНФ по таблице
истинности логической функции.
1) Выбрать из таблицы истинности те строки, в которых
значение формулы - "Ложь"(0).
2) Для каждой выбранной строки составить дизъюнкцию
переменных или их отрицаний так, чтобы эта
дизъюнкция была ложной (для этого переменные,
которые в соответствующей строке имеют значение
"Истина" (1) нужно взять с отрицанием, а переменные,
имеющие значение "Ложь" - без отрицания).
3) Составить конъюнкцию полученных дизъюнкций.
22. + Определение полинома (многочлена)
Жегалкина.
Полиномом (многочленом) Жегалкина от п переменных
называется функция
P =
x
x
2
+ ...
n
x
n
+
n
+1
x
x
2
+...+
n +C
2
n
x
n-1
x
n
+ ...+
2n-1
x
x
2
..xn. Всего здесь 2
п
слагаемых. Напомним,
что + сейчас означает сложение по модулю 2,
коэффициенты
,
n
-1
являются константами
(равными нулю или единице).
Теорема. Любая функция п переменных может быть
представлена полиномом Жегалкина и это
представление единственно.
Доказательство. Любая функция f(x
1
, x
2
, …, x
n
) имеет
свою таблицу истинности. Запишем сначала данную
функцию в виде полинома Жегалкина с
неопределенными коэффициентами. Затем по очереди
подставляем всевозможные наборы переменных и
находим коэффициенты. Легко видеть, что за каждую
подстановку находим только один коэффициент. Так как
число наборов равно числу коэффициентов (и равно 2
п
),
отсюда следует утверждение теоремы.
Доказательство этой теоремы показывает, как по таблице
истинности построить полином Жегалкина.
Имеется 2-й способ нахождения полинома Жегалкина
для функций, заданных в виде ДНФ. Этот способ основан
на том, что х+1 = . Если функция задана в виде ДНФ,
то сначала убираем дизъюнкцию, используя при этом
правило де Моргана, а все отрицания заменяем
прибавлением единицы. После этого раскрываем скобки
по обычным правилам, при этом учитываем, что четное
число одинаковых слагаемых равно нулю (так как х+ х =
0), а нечетное число одинаковых слагаемых равно
одному такому слагаемому.
23. -Эквивалентности перевода дизъюнктивных и
конъюнктивных форм в полином Жегалкина.
24. - Правила перевода дизъюнктивных и
конъюнктивных форм в полином Жегалкина.
25. - Метод неопределенных коэффициентов
нахождения коэффициентов многочлена Жегалкина.
Если функция зависит от п переменных, то
выписывает общий вид искомого многочлена
Жегалкина с неизвестными коэффициентами:
составляем систему линейных уравнений, содержащую
2
п
неизвестных:
Неизвестные коэффициенты
находят из решения системы.
26. + Суперпозиция функций. Замыкание набора
функций. Замкнутые классы функций.
Пусть имеется некоторый набор K, состоящий из
конечного числа булевых функций. Суперпозицией
функций из этого набора называются новые функции,
полученные с помощью конечного числа применения
двух операций;
- можно переименовать любую переменную, входящую в
функцию из K;
- вместо любой переменной можно поставить функцию
из набора K или уже образованную ранее суперпозицию.
Суперпозицию еще иначе называют сложной функцией.
Пример. Если дана одна функция х|y (штрих
Шеффера), то ее суперпозициями, в частности, будут
следующие функции x|x, x|(x|y), x|(y|z) и т. д.
Замыканием набора функций из K называется
множество всех суперпозиций. Класс функций K
называется замкнутым, если его замыкание совпадает с
ним самим.
Т
0
– это набор всех тех логических функций, которые на
нулевом наборе принимают значение 0 (Т
0
– это класс
функций, сохраняющих 0);
Т
1
– это набор всех логических функций, которые на
единичном наборе принимают значение 1 (Т
1
– это класс
функций, сохраняющих единицу) (заметим, что число
функций от п переменных принадлежащих классам Т
0
и
Т
1
равно 2
2n-1
);
L – класс линейных функций т.nе. функций, для которых
полином Жегалкина содержит только первые степени
переменных;
М – класс монотонных функций.
Теорема. Классы функций Т
0
, Т
1
, L, M, S замкнуты.
Это утверждение следует непосредственно из
определения самих этих классов, а также из определения
замкнутости.
27. +Понятие полного набора функций. Понятие
базиса.
Существуют наборы логических функций, с помощью
которых можно выразить любые другие логические
функции. Такие наборы называются функционально
полными наборами или базисами.
Базисом называется совокупность элементов, с
помощью которых схемотехнически можно реализовать
устройство любой сложности.
Наиболее известный и изученный базис - набор И, ИЛИ,
НЕ (конъюнкция, дизъюнкция, отрицание). Множество
всех логических функций, на котором определены эти
три операции, называется булевой алгеброй.
Пример. Дана одна функция х|y (штрих Шеффера), то
ее суперпозициями, в частности, будут следующие
функции x|x, x|(x|y), x|(y|z) и т.nд.
Замыканием набора функций из K называется множество
всех суперпозиций. Класс функций K называется
замкнутым, если его замыкание совпадает с ним самим.
Набор функций называется полным, если его замыкание
совпадает со всеми логическими функциями. Иначе
говоря, полный набор – это множество таких функций,
через которые можно выразить все остальные булевы
функции.
Неизбыточный полный набор функций называется
базисом (“неизбыточный” означает, что если какую-то
функцию удалить из набора, то этот набор перестанет
быть полным).
28. +Пять основных классов функций.
Теорема Поста. Для того чтобы некоторый набор
функций K был полным, необходимо и достаточно,
чтобы в него входили функции, не принадлежащие
каждому из классов T
0
, T
1
, L, M, S.
Т
0
– это набор всех тех логических функций, которые на
нулевом наборе принимают значение 0 (Т
0
– это класс
функций, сохраняющих 0);
Т
1
– это набор всех логических функций, которые на
единичном наборе принимают значение 1 (Т
1
– это класс
функций, сохраняющих единицу) (заметим, что число
функций от п переменных принадлежащих классам Т
0
и
Т
1
равно 22n-1);
L – класс линейных функций т. е. функций, для которых
полином Жегалкина содержит только первые степени
переменных;
М – класс монотонных функций. Опишем класс этих
функций более подробно. Пусть имеются 2 набора из п
переменных: s
1
= (x
1
, x
2
,..., x
n
).
s
1
= (х
1
, х
2
,…, х
п
) и s 2 = (y
1
, y
2
,…, y
п
). Будем говорить, что
набор s 1 меньше набора s2 (s
1
£ s
2
), если все х
i
£ y
i
.
Очевидно, что не все наборы из п переменных сравнимы
между собой (например, при п = 2 наборы (0,1) и (1,0) не
сравнимы между собой). Функция от п переменных
называется монотонной, если на меньшем наборе она
принимает меньшее или равное значение. Разумеется,
эти неравенства должны проверяться только на
сравнимых наборах. Понятно, что несравнимые наборы –
это те, в которых есть некоторые координаты типа (0,1) в
одном наборе и (1,0) в другом на соответствующих
местах (в дискретной математике монотонные функции
это только как бы “монотонно возрастающие функции”,
“монотонно убывающие” функции здесь не
рассматриваются).
Класс Sn– класс самодвойственных функций. Функция
п переменных называется самодвойственной, если на
противоположных наборах она принимает
противоположные значения, т.nе. самодвойственная
функция f(x
1
, x
2
,…,x
n
) удовлетворяет условию f (x
1
,x
2
, ...,
x
n
) =. Например, функции f
1,
f
2
-
являются самодвойственными, а функции f
3,
f
4
– не
являются. Нетрудно устанавливается следующий факт.
29. + Определение самодвойственной функции.
Носитель функции. Мощность носителя. Лемма о
мощности носителя.
Самодвойственная функция - булева функция,
двойственная сама к себе. Функцией, двойственной к
функции , называется функция
.
Значит, функция является
самодвойственной, если
.
Другими словами самодвойственная функция на
противоположных друг другу наборах значений
аргументов принимает противоположные значения.
Множество самодвойственных функций обозначается
символом S.
Определение 8.10. Носителем функции
f
называется
совокупность наборов, на которых функция обращается
в 1.
Определение 8.11. Мощностью носителя называется
количество единиц в векторе значений функции.
Лемма 8.2. Если мощность носителя функции отлична от
половины, то функция не является линейной. Обратное
не верно.
Таким образом, если количество единиц в векторе
значений функции отлично от половины, то функция не
является линейной. Если же единиц ровно половина, то
для проверки на линейность нужно представить
функцию в виде многочлена Жигалкина и проверить
отсутствие произведений переменных.
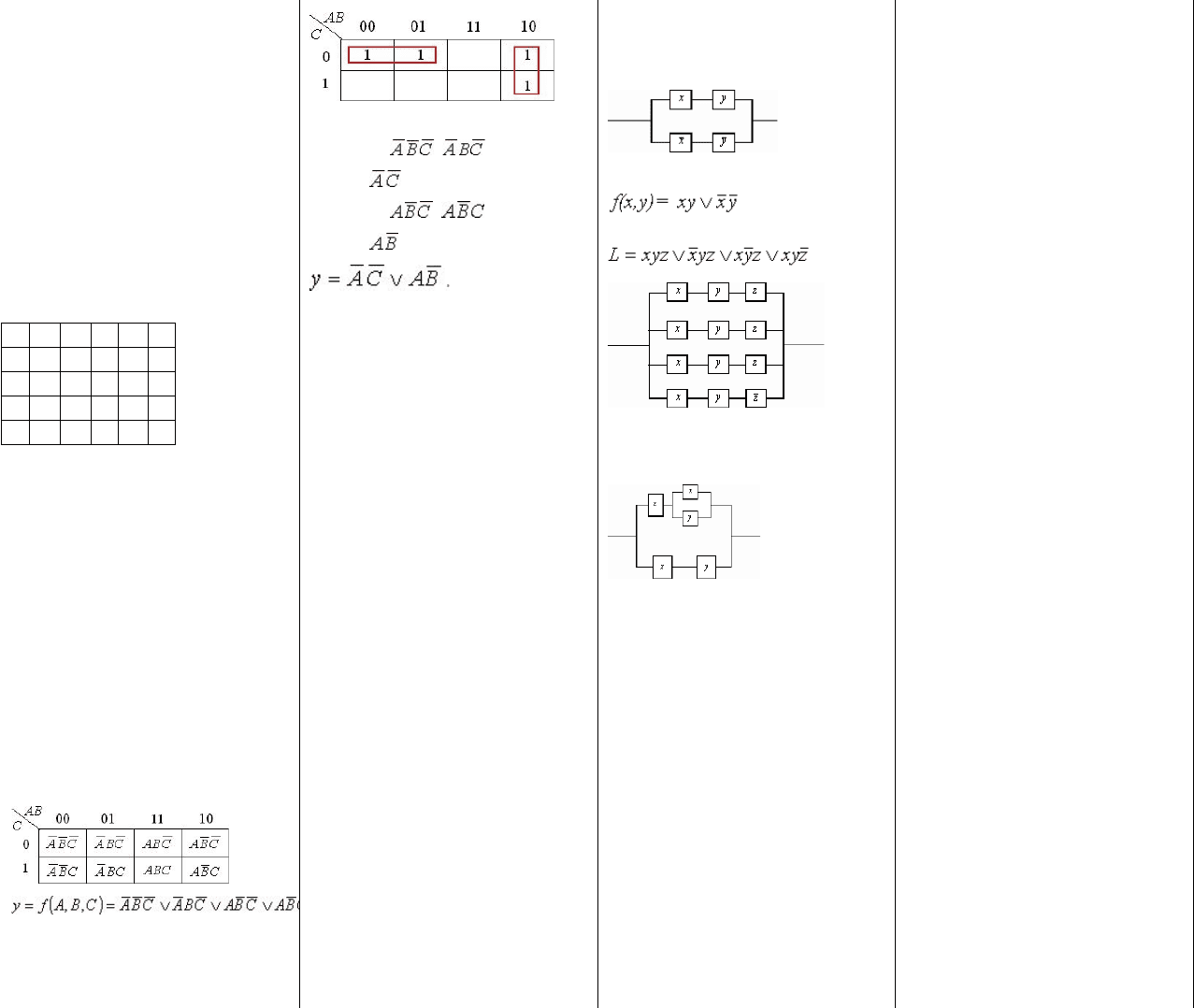
30. +Теорема Поста. Таблица Поста. Следствие из
теоремы Поста о числе базисных функций в наборе.
Теорема Поста. Для того чтобы некоторый набор
функций K был полным, необходимо и достаточно,
чтобы в него входили функции, не принадлежащие
каждому из классов T
0
, T
1
, L, M, S.
Заметим, что необходимость этого утверждения
очевидна, так как если бы все функции из набора К
входили в один из перечисленных классов, то и все
суперпозиции, а значит, и замыкание набора входило бы
в этот класс и класс К не мог быть полным.
Из этой теоремы следует довольно простой способ
выяснения полноты некоторого набора функций. Для
каждой из этих функций выясняется принадлежность к
перечисленным выше классам. Результаты заносятся в
так называемую таблицу Поста (в нашем
примере эта таблица
составлена для 4-х функций,
причем знаком “+”
отмечается принадлежность
функции соответствующему
классу, знак “–” означает,
что функция в него не
входит).
f T
0
T
1
L M S
f
1
+ – + – –
f
2
+ – – – +
f
3
– + – – –
f
4
+ + – + –
В соответствии с теоремой Поста набор функций будет
полным тогда и только тогда, когда в каждом столбце
таблицы Поста имеется хотя бы один минус. Таким
образом, из приведенной таблицы следует, что данные 4
функции образуют полный набор, но эти функции не
являются базисом. Из этих функций можно образовать 2
базиса: f
3
, f
1
и f
3
, f
2
. Полными наборами будут любые
наборы содержащие, какой-либо базис.
Непосредственно из таблицы Поста следует, что число
базисных функций не может быть больше 5.
31. +Актуальность минимизации логических
функций.
Минимизация логических функций необходима для
упрощения сложных выражений этих самых функций,
например, сложные логические функции могут
отображаться в две-три и более строк (допустим, на
листе формата А4). Понятно, что сразу приступать к
схемной реализации таких функций по большому счету
тупо. Минимизировать логические функции можно с
помощью всяких правил и законов алгебры логики, а так
же можно с помощью так называемых карт Карно.
32. + Минимизация СДНФ методом карт Карно.
Среди формальных методов большое распространение
получил метод Карно и метод Квайна. Метод Карно
основан на представлении исходной функции, заданной
в форме ДСНФ, в виде карты следующего вида:
Пусть задана функция 3-х переменных
Заданную функцию представим с помощью карты
Карно:
Затем производится объединение 2-х, 4-х или 8-ми
единиц. В данном случае объединение двух единиц по
горизонтали соответствует операции склеивания над
конституентами и , в результате
которой исключается переменная B и получена
импликанта .Объединение двух единиц по
вертикали соответствует операции склеивания над
конституентами и , в результате
которой исключена переменная С и будет получена
импликанта . Следовательно, минимальная форма
заданной функции примет следующий вид:
33. + Понятие функционального элемента.
Определение схемы. Необходимое и достаточное
условие существования схемы.
Пусть имеется некоторое устройство, внутренняя
структура которого нас не интересует, а известно лишь,
что оно имеет n упорядоченных входов (занумерованных
числами от 1 до n) и один “выход”. На каждый из входов
может подаваться один из двух сигналов: 0 или 1
(“отсутствие тока” или “наличие его”) и при каждом
наборе сигналов на входе возникает один из двух
сигналов 0 или 1 на выходе. Такое устройство
называется функциональным элементом (ФЭ).
Если имеется несколько ФЭ, то из них можно получать
новые сложные ФЭ (например, один из входов ФЭ
можно соединить с выходом другого. В этом случае
полученное соединение соответствует суперпозиции
двух функций. Можно также соединять некоторые
входы, что означает отождествление некоторых
переменных).
Соединение нескольких ФЭ называется схемой.
Но не всякое соединение ФЭ является схемой.
Соединение S конечного числа функциональных
элементов является схемой тогда и только тогда, когда
выполнены 3 условия:
- среди ФЭ есть один и только один свободный выход
(т.е. выход, не соединенный ни с каким входом);
- каждый вход любого ФЭ может быть соединен не более
чем с одним выходом другого ФЭ;
- в соединении S нет циклов (т.е. нет такого
упорядоченного набора ФЭ, когда вход следующего
соединен с выходом предыдущего и вход первого
соединен с выходом последнего. Цикл в соединении
иначе называют обратной связью).
34. +Определение релейно-контактной схемы (РКС).
Привести пример.
Релейно-контактной схемой или РКС будем
называть некоторое соединение, состоящее из
следующих элементов:
- переключателей (это могут быть как механические
устройства, так и лампы, электромагнитные реле и т. д.)
Каждый переключатель может принимать значение 1
(через него пройдет ток) или 0 (через него ток не
проходит). Будем считать, что любой переключатель
соответствует либо логической переменной x, либо ;
- проводников, могущих соединять переключатели либо
последовательно, либо параллельно (это соответствует
замене ФЭ, определяющих конъюнкцию или
дизъюнкцию);
- входа и выхода из системы (вход и выход называются
полюсами системы).
Иначе РКС называют переключательной схемой (П-
схемой).
Будем говорить, что конкретная РКС принимает
значение 1 при данных значениях переключателей, если
через нее проходит ток, в противном случае мы считаем,
что она принимает значение 0.
Две РКС считаются равносильными, если они
принимают одинаковые значения при одних и тех же
значениях переключателей.
Очевидно, что любая суперпозиция функций
конъюнкции, дизъюнкции и отрицания может быть
изображена в виде РКС. Например, функции
соответствует следующая
РКС.
Следующая РКС соответствует функции
(в ней 12
переключателей).
После сокращения СДНФ по правилу Блейка можно
получить равносильную формулу: L = xz yz xznn, для
которой РКС будет иметь 6 переключателей. Если
ставить целью уменьшение числа переключателей, то
последнее выражение можно преобразовать к виду L
=n(xn y)nz xynn(РКС будет иметь 5 переключателей).
«Дискретный анализ»
1. Понятие множества, элементов множества,
подмножество, универсальное множество, пустое
множество.
2. Операции над множествами и их семействами:
объединение, пересечение, дополнение, разность.
3. Понятие графа. Полный граф. Вершина, степень
вершины.
4. Теорема о сумме степеней вершин графа. Теорема о
числе нечетных вершин графа.
5. Цикл. Путь. Длина пути. Связность графа. Мост.
Деревья, лес.
6. Плоский граф. Формула Эйлера о числе ребер и
числе граней для плоского представления плоского
связного графа.
7. Эйлеровы графы и Эйлеровы пути.
8. Лабиринты. Циклы.
9. Гамильтоновы графы, гамильтоновы пути и циклы.
10. Понятие алгебры логики, булевой алгебры. История
создания алгебры логики.
11. Понятие высказывания. Операции над
высказываниями (дизъюнкция, конъюнкция, отрицание).
12. Унарные операции, бинарные операции, n-арные
операции.
13. Понятие набора. Понятие «значения функции на
данном наборе».
14. Методика построения таблиц истинности логических
функций.
15. Понятие дизъюнктивной нормальной формы (ДНФ).
16. Понятие конъюнктивной нормальной формы (КНФ).
17. Понятие совершенной дизъюнктивной нормальной
формы (СДНФ).
18. Понятие совершенной конъюнктивной нормальной
формы (СКНФ).
19. Правила приведения произвольной формы алгебры
логики к СДНФ и СКНФ.
20. Методика построения СДНФ по таблице истинности
логической функции.
21. Методика построения СКНФ по таблице истинности
логической функции.
22. Определение полинома (многочлена) Жегалкина.
23. Эквивалентности перевода дизъюнктивных и
конъюнктивных форм в полином Жегалкина.
24. Правила перевода дизъюнктивных и конъюнктивных
форм в полином Жегалкина.
25. Метод неопределенных коэффициентов нахождения
коэффициентов многочлена Жегалкина.
26. Суперпозиция функций. Замыкание набора функций.
Замкнутые классы функций.
27. Понятие полного набора функций. Понятие базиса.
28. Пять основных классов функций.
29. Определение самодвойственной функции. Носитель
функции. Мощность носителя. Лемма о мощности
носителя.
30. Теорема Поста. Таблица Поста. Следствие из
теоремы Поста о числе базисных функций в наборе.
31. Актуальность минимизации логических функций.
32. Минимизация СДНФ методом карт Карно.
33. Понятие функционального элемента. Определение
схемы. Необходимое и достаточное условие
существования схемы.
34. Определение релейно-контактной схемы (РКС).
Привести пример.
