Шпора по комбинаторике. 3 семестр

Подождите немного. Документ загружается.

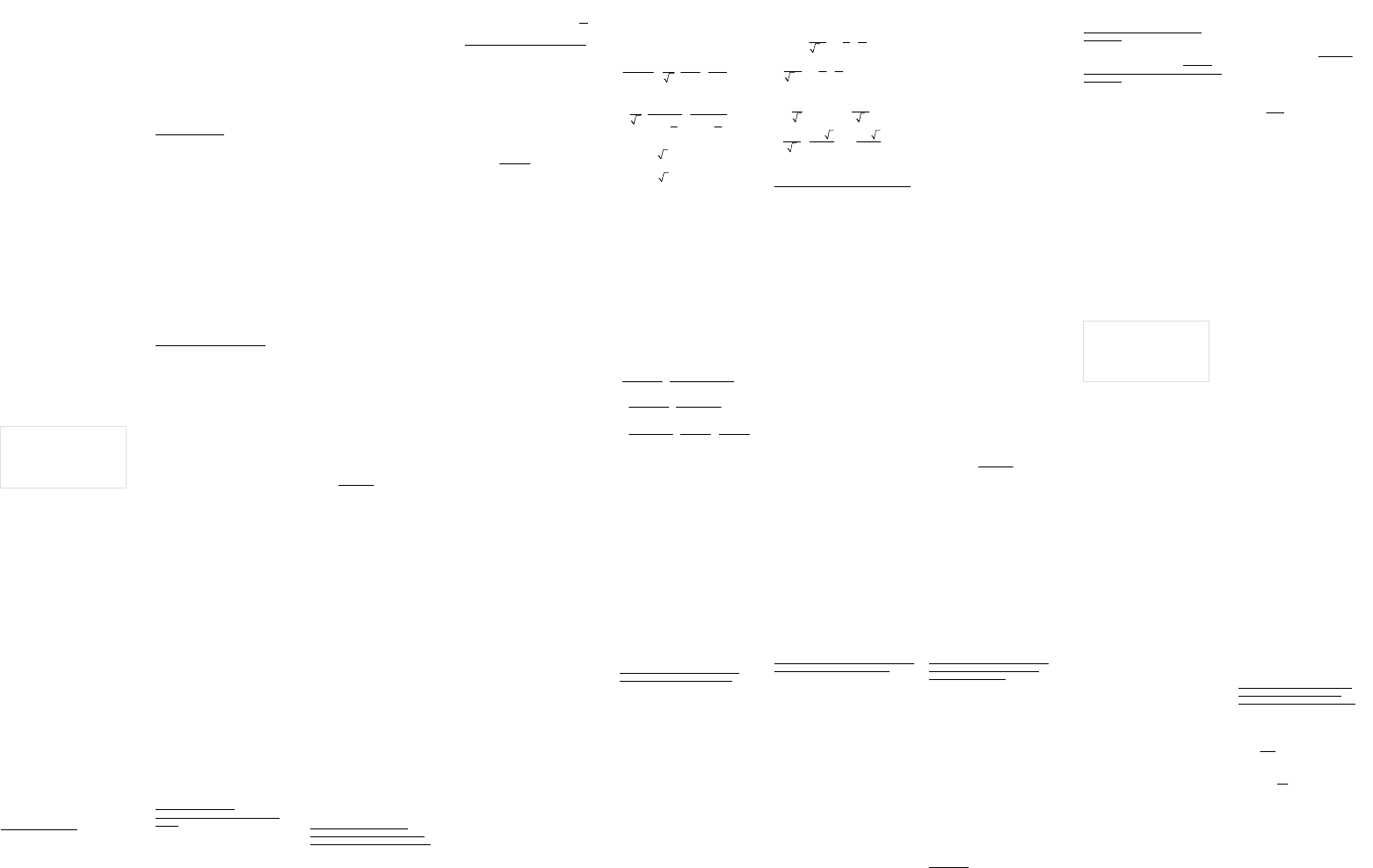
((1))

Метод производящих функций.

В комбинаторных задачах на подсчет

числа объектов при ограничении

решением часто является

последовательности

0 1 2

, , ,..., (1)

a a a a

,(а>=1), где

число искомых объектов. Каждой

числовой последовательности вида

(1) ставится в соответствие функция

действительного или комплексного

аргумента так, чтобы обычная

операция над последовательностями

соответствовала простым операциям

над соответствующими функциями.

Один из способов отображений

последовательность в функцию в

форме степенного ряда называется

производящей функцией.

0 1 2

( ) ... (2)

n i

А х a x a a x a x a x





     



Ряд (2) является формальным, т.е. 1)

это удобная форма записи

последовательности (1) 2) не

существенно для каких значений х

ряд сходится 3) мы не будем

вычислять значение суммы ряда для

конкретного х. Будем использовать

(2) для 1) выполнения операций на

рядах 2) определять коэффициенты

при отдельных степенях х 3) изучать

свойства последовательности вида

(1).

Операции над ПФ.

Для произвольных рядов А(x) и B(x)

определены

1)операция сложения

( ) ( ) ( ) ( )

n n

A x B x D x a b x





   



2)умножение на число р(действ или

комплекс)

( ) ( )

pA x D x pa x





 



3)произведение коши

0 0

( ) ( ) ( ) ,

...

n i n i n n

A x B x D x d x

d a b a b a b









 

   



Замечание: Операции сложения и

умножения рядов удовлетворяют

законом ассоциативности,

коммутативности и

дистрибутивности умножения

относительно сложения. Один из

видов производящих функций это

экспоненциальная.

( )

E x







вывод ПФ для чисел Фибоначчи

Чтобы вывести формулы ПФ

2 3 4

( ) 1 2 3 5 ..Fib s s s s s     

умно

жим обе части равенства на

s s

Получим

2 2 3 4 5

2 3 4 5 2 3 4 5

( ) 2 3 5 ..

2 3 .. 2 3 5 8 ...

s s Fib s s s s s s

s s s s s s s s s

       

          

или

( ) ( ) ( ) 1s s Fib s Fib s  

откуда

( )

Fib s

s s



 

эту формулу

можно понимать как композицию

двух ПФ

 

1 s



s s

, т.е.

2 2 2 2 3

( ) 1 ( ) ( ) ( ) ..Fib s s s s s s s       

Полезнее представить дробь в виде

суммы 2х дробей:

2 1

1 2

1 1 1 1

1 1 1

1 1

s s s s s s

s s

 

  

 

   

 

 

 

 

 

   

 

 

   

 

   

 

, где

 

1 5 / 2 s   

 

1 5 / 2 s   

- корни Ур-ия

1 0s s  

. Из последнего

разложения получаем

1 1

2 2

( ) 1 ..

1 ..

s s

Fib s

s s

 

    

 

 

 

   

 

 

Поэтому

 

1 1 1 1

1 2 1 2

1 1

5 5

1 5 1 5

2 2

n n n n

n n

f s s s s

       

 



    

 

   



   

 

    

   

 

   

 

1 2

1s s 

Использование ПФ в теории графов.

Опр: Бинарным деревом k c n

вершинами называют либо пустое

дерево

T 

n=0, или тройку

, ,T L r P 

, где r - корень

дерева, L – левое поддерево с l

вершинами, P – право поддерево с p

вершинами. Всего в этом дереве

l+1+p=n вершин.

Различие между бинарным деревом

и простым состоит в том, что дерево

не может быть пустым и каждый

узел дерева может иметь правое

число поддеревьев бинарное древо

может быть пустым и каждый его

узел может содержать 0, 1, 2

поддерева.

Опр: Будем говорить, что деревья T1

и Т2 изоморфны (T1~T2) если

1 2

T T 

или T1=<L1,r1,P1>

T2=<L2,r2,P2>. L1~L2 P1~P2.

Задача подсчета бин деревьев

порядка n: Найдем число бинарных

деревьев с n- вершинами, пусть Ск –

это число не изоморфных бинарных

деревьев с к- вершинами. Задача

подсчета числа помеченных графов

порядка n : Дано число N вершин.

Требуется посчитать количество

различных помеченных графов

с N вершинами (т.е. вершины графа

помечены различными числами от 1

до N, и графы сравниваются с учётом

этой покраски вершин). Рёбра графа

неориентированы, петли и кратные

рёбра запрещены.Рассмотрим

множество всех возможных рёбер

графа. Для любого ребра (i,j)

положим, что i<j (основываясь на

неориентированности графа и

отсутствии петель). Тогда множество

всех возможных рёбер графа имеет

мощность

, т.е.

 

N N 

.Поскольку любой помеченный граф

однозначно определяется своими

рёбрами, то количество помеченных

графов с вершинами равно:

 

N N





((4)) начало

((3))Вывод чисел Каталана.

(примение)

Порядок вычислений

арифметических выражениях

задается расстановкой скобок,

например: (3-1)*(4+(15-9))*(2+6)).

Если стереть все элементы

выражения, за исключением скобок,

то оставшиеся скобки образуют

правильную скобочную структуру: ( )

( ( ) ( ) ). Вот все правильные

скобочные структуры с числом пар

скобок 1, 2, 3:

Числом К.

наз-ся число

различных скобочных структур из n

пар скобок.

Если

=1, то последовательность

чисел К. равна: 1,1,3,5,14,42,132,…

Применение чисел Каталана.

Числа К. перечисляют самые

разнообразные комбинаторные

объекты. Реализация чисел К.

осуществляется диагональной

триангуляцией(это разбиение

многоугольника на треугольники

непересекающимися

диагоналями).Еще одна важная

реализация чисел К. связана с

путями Дика на плоскости (путем

Дика называется непрерывная

ломанная в верхней полуплоскости,

составленная из векторов (1,1) и (1,-

1),начинающаяся в начале координат

и заканчивающаяся на оси абсцисс).

Совершенно ясно, как

устанавливается соответствие

между путями Дика и правильными

скобочными структурами : нужно

сопоставить вектору (1,1) левую

скобку, а вектору (1,-1) правую.

Тогда условие, что путь лежит в

верхней полуплоскости и

заканчивается на оси абсцисс, и есть

в точности условие правильности

скобочной структуры. Поэтому число

путей Дика из 2n звеньев

равно n-му числу Каталана

((4))Свойства биномиальных

коэффициентов.

док-ва 4-мя способами. 1)

Использование опр-е биномиального

коэфф. 2) Комбинаторный подход.

Рассматриваются комбинации

различных условий, которые

разбиваются на непересекающиеся

полосы. 3) Использование ПФ. 4)

Геометрический подход – метод

траекторий.

[1]

k n k

n n

C C





Док-во 1) (опр)

( )! !

n k k

n n

C C

n k k



 



Док-во 2) (комбин.) Если выбрать из n

различных предметов некоторое k

сочетание, то останется

дополнительное сочетание из n-k

элементов. А дополнительным к n-k

сочетанию является исходное k

сочетание. Таким образом, k

сочетание и n-k сочетание образует

взаимно дополнительные пары,

поэтому их число одинаковое. ч.т.д.

Док-во 3) (траекторий) Рассмотрим

прямоугольную сетку квадратов

размером

m n

. Это шахматный

город, состоящий из

m n

кварталов с n-1 горизонтальными и

m-1 вертикальными улицами.

Необходимо найти каково число

различных кратчайших путей на этой

сетке от (0;0) до (m;n). Каждый

кратчайший путь из (0;0) в (m;n)

состоит из m+n отрезков, причем из

них m – горизонтальных и n –

вертикальных путей. Различные пути

отличаются порядком чередования

горизонтальных и вертикальных

отрезков, поэтому общее число

путей равно числу способов,

которыми можно из m+n отрезков

выбрать n вертикалей. А если бы мы

выбирали m горизонтальных, то

число способов было бы тем же, но

формула другая.

n m

m n m n

C C

 



[2]

1 1

k k k

n n n

C C C



 

 

1) (опр)

 

( 1)! ( 1)!

!( 1 )! ( 1)!( 1 1)!

( 1)! ( 1)!

!( 1)! ( 1)!( )!

( 1)!

( 1)! !

!( )! !( )! !( )!

n n

k n k k n k

n n

k n k k n k

n n k

k n n

k n k k n k k n k

 

 

     

 

  

   

 



   

  

2) (комбин.) Составим k сочетания из

n элементов

1 2 3

, , ..

a a a a

и разобьем

их на 2 класса. Пусть в 1-й из них

войдут сочетания, содержащие

элемент

, а во второй сочетания

без этого элемента. Если из каждого

сочетания 1-го класса убрать

, то

получится k-1 сочетания,

составленные из элементов

1 2 3 1

, , ..

a a a a



. Число таких

комбинаций



. Во втором классе

собраны k сочетания из n-1

элемента, и их число поэтому



Поскольку любое паросочетание из

элементов

1 2 3

, , ..

a a a a

принадлежит только одному из этих

2-х классов и общее число сочетаний

, то приходим к равенству

1 1

k k k

n n n

C C C



 

 

[3]

0 1

.. 2

n n

n n n

C C C   

1) (ПФ) Известно что для

биномиальных коэффициентов ПФ

является

(1 )

k k n

C x x



 



. Пусть

х=1, тогда

(1) (1 1) 2

k k n n



  



Число элементов с

повторениями. Разобьем все

элементы на классы, отнеся в k класс

те, в которые входят элементы

первого типа и n-k элементов 2-го

типа. Это всевозможные

паросочетания k элементов первого

типа n-k элементов второго типа,

таких перестановок

( , )

!( )!

P k n k C

k n k

  



Перебирая все значения k от 0 до n

получим

0 1

...

n n n

C C C  

. С другой

стороны это число

3) (траек)

Рассмотрим все пути, ведущие из А

к точке вида

 

B k n k

где

0 k n 

. Эти пути разбиваются на

классы, в зависимости от того, в

какой точке заканчиваются. В саму

точку

ведет

( , )

P n n k C 

путей. Подсчитаем общее число

таких путей. Длина кратчайшего

пути n, зашифруем кратчайший путь

последовательностью 0 и 1, причем

сопоставим 0 горизонтальным

отрезком пути, а вертикальным

единицы. Число n-

последовательностей 0 и 1 будет

. и в тоже время пути различны,

значит k от о до n, сумма путей до

есть сумма

0 1

n n n

C C C  

[4]

0 1

.. ( 1) 0

n n

n n n

C C C    

1) (ПФ)

0 0

[ 1] ( 1) 0

n n

k n k k

n n

k k

C x x C

 

    

 

[5]

( 1) 0

k k

k C



 



(ПФ) Известно, что

(1 )

k n n

C x x



 



дифф-ем по х обе

части равенства:

1 1

(1 )

k k n

kC x n x

 



 



пусть х=-1

 

1 0







 



((6))Рекуррентные соотношения.

Рекуррентные соотношения – это

равенства, определяющие

последовательность рекурсивно,

каждый элемент

последовательности определяется

как функция от предыдущих

элементов. Дифференциальные

уравнения – это отдельный вид

рекуррентных соотношений. Пример

РС – это формула чисел Фибоначчи.

Другие примеры РС могут иметь

хаотичное поведение и встречаются

в нелинейном анализе. Линейные

однородные РС с постоянным

коэффициентами. Рс порядка k:

1 1 2 2

...

n k n k n k k n

f a f a f a f a

    

    

Если а=0, то Рс однородная. Если

известны начальные значения

0 1

f f



, то говорят, что

последовательность задана

однозначно.

Общее решение РС. Рассмотрим

решение РС второго порядка.

2 1 1 2

( )

n n n

f a f a f

 

  

Решение РС

такого типа основано на двух типах

предложений. Предложение 1: если

являются решениями (*), то

любые числа А,В

n n n

f Ax By 

тоже является решением данного РС.

Предложение 2: если число

явл.

корнем квадратного уравнения

1 1 2

r ra a 

, то послед.

2 1

1, , ...,

r r r



явл. решением (*).

Замечание: наряду с

последовательностью

{ }



любая

последовательность вида

n m

f r n N



 

также являются

решениями (*)

Случай, когда корни

характеристического уравнения

равны, то решение получается в

виде

1 2

( )

r C nC





. Докажем это.

По теореме Виета:

1 2

r a r a 

имеет

1 2

r r

, если

1 2 1

2 , a r a r 

тогда

2 2

1 1

2r r r r 

и РС имеет вид

2 1 1 1

n n n

f r f r f

 

 

Проверим что

y nr





действ явл решением

данного соотношения

1 1

2 1

( 1)

( 2)

y n r



 

Получим

1 2 1

1 1 1 1 1

1 1 1

( 2) 2 ( 1)

( 2) 2( 1)

2 2 2

n n n

n r r n r r n nr

n r n r nr

n n n

 

  

    

   

Тождество,

y

явл решением.

Линейные неоднородные

рекуррентные соотношения с

постоянными коэффициентами.

Если РС неоднородное, то его

частное решение может быть

найдено методом неопределённых

коэффициентов, а решение будет

суммой общего и частного решения.

Ещё один способ называется

символической дифференциацией.

Например, рассмотрим РС

2 1

1, 1

n n

a a n n

a a



 

   

 

далее вычтем

из второго первое

2 1 1

2 1

2 0

n n n n

n n n

a a a a

a a a

  

 

  

  

. В общем

случае, если линейная

рекурентность имеет вид

1 1 2 2

... ( )

n k k n k k n k

f a f a f

a f p n

      

  

  

. Здесь

применение символической

дифференциации n раз приведет к

однородному РС.

((7))Генерирование

комбинаторных

последовательностей

Алгоритм генерирования состоит,

как правило, из трёх компонентов: 1)

выбор начальной конфигурации 2)

трансформация одного объекта в

следующий 3) условия окончания.

Генерирование перестановок.

Пусть имеется

(1, 2,3,.., )X n

Генерирование перестановок в

лексикографическом порядке.

Последовательность перестановок

на множестве Х, представленных в

лексикографическом порядке, если

она записана в порядке возрастания.

Определение. Если х=(х1,х2,…,хn)

y=(y1,y2,..,yn), то говорят что х

лексикографически меньше y, если

для некоторого k>=1 имеет место

j j k k

x y j k x y   

Алгоритм: записываем 1234, находим

самую правую убывающую

подпоследовательность (это просто

цифра 4), и выбираем из этой

подпоследовательности

минимальное число, и меняем

местами с тем числом, которое стоит

прям перед данной

подпоследовательность (4 выделили,

минимальное та же 4, число перед

подпоследовательностью это 3,

меняем местами, и так далее). После

перастановки минимального из

подпослед. и числа перед

подпослед. остальные цифры

переписываем по возрастанию.

Генерирование перестановок в анти

лексикографическом порядке.

Определение. Если х и у

перестановки, то говорят, что х анти

лексикографически меньше у, если и

только если

x , ( ')

j k k

k n y j k x y      

Например, 1234<’2134.

Алгоритм для генерации

перестановок в

антилексикографическом порядке

может базироваться на двух

утверждениях: 1.Если множество

перестановок P упорядочено

антилексикографически, то

начальная и конечная перестановки -

это соответственно (1, 2, …, n) и (n,

n-1,…,1). 2.Упорядоченная

антилексикографически

последовательность перестановок

по значению последнего элемента в

них может быть разбита на n блоков

длины (n-1)!. При этом q-й блок на

последнем месте имеет элемент,

равный (n-q+1), а первые n-1

позиций этого блока определяют

последовательность перестановок

множества {1,2,…,n}\{q} в

антилексикографическом порядке.

Генерирование перестановок с

однократной транспозицией

соседних элементов.

Пусть построена

последовательность перестановок

элементов от 2 до n, обладающая

однократной композицией соседних

элементов. Так для n=3

перестановки будут: 23; 32. Тогда

требуемая последовательность

перестановок 1,2,3… n мы получим,

вставляя элемент 1 всеми

возможными способами каждую

перестановку из элементов от 2 до n.

123, 132, 213, 312, 231, 321

(чередуются 23,32) В общем виде

элемент перемещается между

первой и последней позицией (n-1)!

раз по переменным вперед и назад.

Недостаток метода:

последовательность перестановок

строится целиком и только после

окончания построения её можно

считывать, поэтому метод требует

большого объёма памяти.

Коды Грея

Ранее мы рассматривали

рекурсивный алгоритм перебора 0-1

наборов. Этот алгоритм позволяет

перебирать все наборы B

так, чтобы

каждый следующий набор отличался

от предыдущего только в одном

разряде. Построенная с помощью

этого алгоритма последовательность

наборов (приводится в таблице)

называется кодом Грея. Вообще, n-

разрядный код Грея — это

упорядоченная (возможно,

циклическая) последовательность,

состоящая из 2

n-разрядных

кодовых слов, каждое из которых

отличается от соседнего в одном

разряде.

Приведем еще один (на этот раз

нерекуррентный) алгоритм

генерации кодов Грея. Будем

рассматривать бинарные коды Грея

порядка n. Итак, на вход алгоритма

подается единственное число n,

которое указывает порядок кода

Грея. По ходу выполнения алгоритма

мы получим последовательность

всех подмножеств n-элементного

множества, в которой каждое

последующее подмножество

получается из предыдущего

добавлением или удалением

единственного элемента

(наименьшим возможным

изменением) — код Грея. При этом

каждое подмножество будет

представляться бинарной

последовательностью B[1], …, B[n].

Генерирование k -элементных

подмножеств множества в

лексикографическом порядке:

Метод: генер. k-элементное

подмнож: Сформируем из

{1,2,3,4,5,6} подмнож

| 3 |

3!3!

C  

(123,124,125,126,134,135,136,145,146

,156,234…) Начнем составлять

, 1,

x i i k 

, ищем первый

компонент, который можно

увеличить, если такой не найдется -

заканчиваем процедуру при i=k. Если

увеличивать на 1, то для всех

следующих за

комп. продолж.

натур. ряд

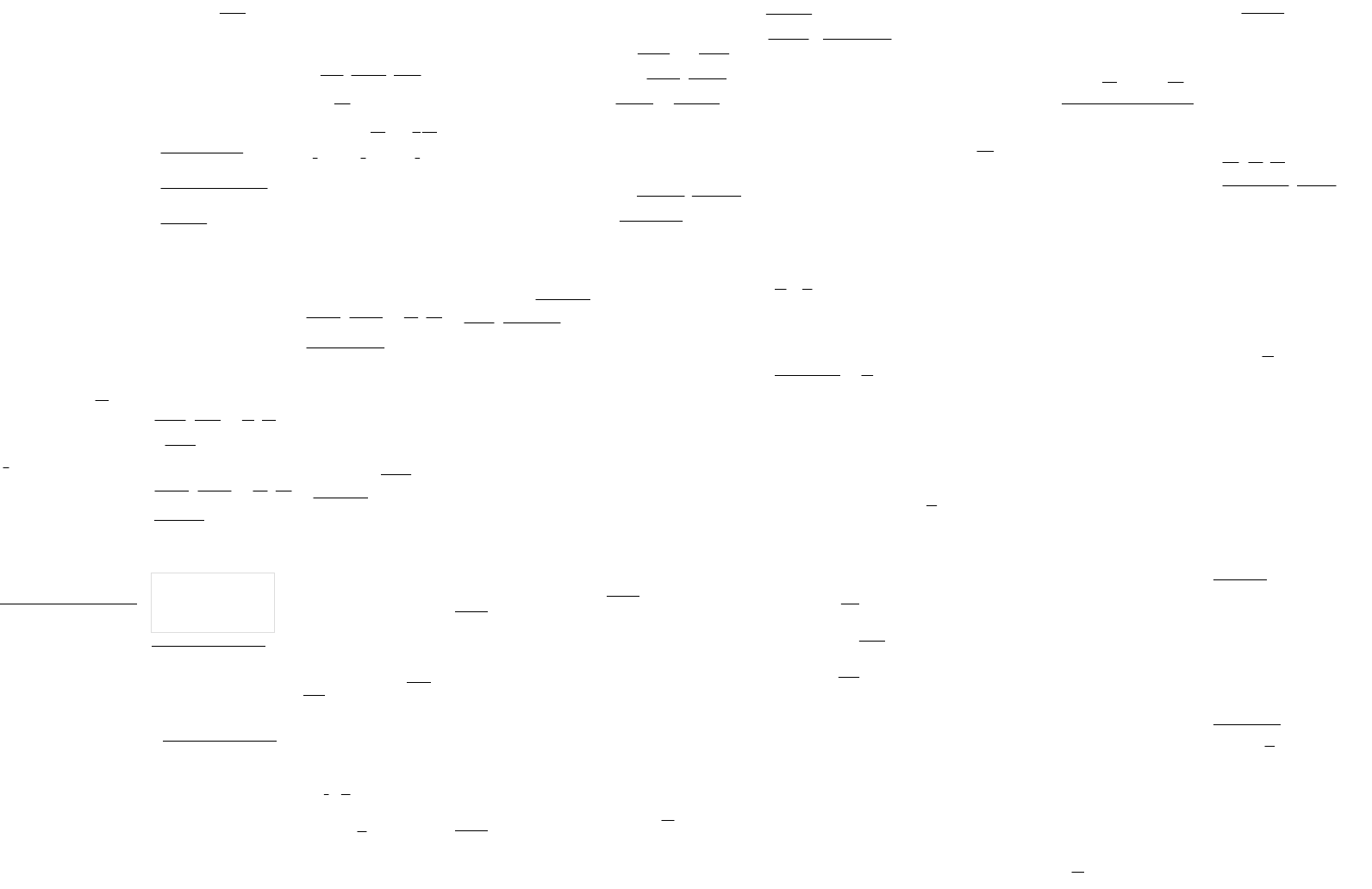
((2))

Операции над комбинаторными

последовательностями.

Пусть

, ,

k k k

a b d

комбинаторные

последовательности. A(x), B(x), D(x)

их ПФ.

1) Линейные операции. Если

или

 

константы, действит. или

комплекс., то

k k k

d a b

 

 

ПФ

имеет вид

D(x)= A(x)+ B(x)

 

2) Свёртка операции Если

то D(x)=A(x)B(x)

k i k i

d a b







3) Сдвиг послед. на фиксир число 1.

Пусть

0, 0, ( 1)

k i

a k i





 













0 1

0 1 2

( ) ..

( ...) ( )

n n i i

k k i

i i k i

B x b x a x a x a x

x a a x a x x a x x A x

 



 





     

     

 



2. Сдвиг в начало. Пусть

k k i

b a





0 2

1 2

1 1

0 0

( ) ...

...

( )

k i i i i

i i i

i i

k k i i

k k

B x a x a x a x a x

a x a x a x

a x a x a x a x

A x a x



  



 

 



 





     

  

 

  

 







 



4. Изменение масштаба

А)

k k

b ka

, k=0,1,…

0 0 0

( ) ( )

( )

( ) ( ( ))

( )

k k k

B x b x ka x x a kx

xd a x

a d x xd A x

xA x

dx dx dx

  



  





   



   

  



Б)





0 0 0

0 0

0 0 0

( )

1 1

1 1 1

( ) ( )

k k

k k k

x x x

k k

a a x

B x b x x

k x k

a t dt a t dt A t dt

x x x



  

  

 

 

  

 

  

  

 

  

5) Оценка сумм с помощью

изменения масштаба.

Докажем что

1 2

1 1

2 1

( )( )

n n

n k k

n n

k k

n k n k C k C

 



 

 

  

 

Оценим сначала правую часть этого

равенства. Пусть

k n

k k

k n

a k C

a kb

b kC









 









k k k n

b kd d C



 

Тогда (по 4А)

( ) '( ) B x xD x

( ) '( ) [ '( )] ' ( '( )

''( )) '( ) ''( )

A x xB x x xD x x D x

xD x xD x x D x

   

  

. т.к.

-1

2 -3

, ( ) (1 ) '( )

( 1)(1 ) ''( ) ( -1)( - 2)(1 )

k n

n n

d C то D x x D x

n x D x n n x



   

    

2 3

( ) ( 1)(1 )

( 1)( 2)(1 )

A x x n x

x n n x



   

   

Подставим

-2 3

1 (1) ( -1)2 ( 1)( 2)2

n n

x A n n n



    

Найдем для этой послед

производящую сумму

0 1 2

2 2 2

( 1)2 ( 1)

( 1)[ .. ]

( 2)! ( 2)!

( 1) ( 1)

0!( 2)! 1!( 3)!

( 2)! ( 1)! 1

.. ( 1)

( 2)!0! 0!( 2)! 1

( 1)! 2 ( 1)!( 1)

...

1!( 3)! 2 ( 2)!( 1)

n k k

n n n

n n C x

n C C C

n n

n n n







  



   

     

 

    

 

  

    

  

   

   

   

 



2 1

1 1 1

2 ... ( 1)

n k

n n n

C n C kC



  



    



0 1 3

3 3 3

( 1)( 2)2 ( 1)( 2)

( 1)( 2)[ .. ]

( 2)( 3)! 1 ( 2)( 3)! 2

( 1)[ ..

0!( 3)! 1 1!( 4)! 2

( 2)( 3)!( 2)

.. ]

0!( 3)!( 2)

n k k

n n n

n n n n C x

n n C C C

n n n n

n n

n n n

n n







  

     

      

     

   

   

  

 

 



2 3 1

1 1 1

( 1)( 2)! 1 2

0!( 3)! 1 2

( 1)( 2)! 3 ( 2)( 1)( 2)!( 1)

2 ..

2!( 4)! 3 ( 2)!( 1)

1 2 2 3 .. ( 1)( 2)

( 1)

n n n

n n

n n n n n n

n n n

C C n n C

k k C



  





   

 

  

      

   

   

        

 



1 1

2 2

1 1

(1) ( 1)

( )

n n

k k

n n

k k

n n

k k

n n

k k

A kC k k C

C k k k k C

 

 

 

 

  

   

 

Это равенство можно переписать в

следующем виде, поменяв пределы

суммирования и на основе свойства

1 0

( )

n n

k n k

n n

k k

kC n k C



 

 

 

получим

сумму

1 2

2 1 2

1 1

2 1

( )

n n

k n k

n n

k k

k C n k C

 

 

 

 

Зная, что

2 2 3

2 2 2 2

2 2

( 1)2 ( 1)( 2)2

2 [2( 1) 2( 1)( 2)]

( 1)2

( 1) ( )

k n n

n n n n

n k

k C n n n

n n n

n n

n n k C



 







    





     

  

   



Откуда получается

3 2 2

( 1)2 ( 1) ( )

n n k

n n n n k C



 





    



6) Частичные суммы Если

( )

, ( )

k i

A x

b a B x



 





Докажем:

0 0 0

0 0 1 0 1 2

2 2

0 1

2 2

0 1

( ) ( )

( ) ( ) ..

(1 ...) ( ...) ...

(1 ...) (1 ..) ..

1 ( )

[| | 1] ( ...)

1 1

k k

k i

k k i

B x b x a x

a a a x a a a x

a x x a x x

a x x a x x x

A x

x a a x

x x

 

  

       

        

         

     

 

  

Дополнительные частичные суммы

Если



( )

A x a x







, то

k i

i k

b a







имеет ПФ

(1) ( )

( )

A xA x

B x







, Док-во:

0 0

0 1 1 2 3

2 3 4 0 1

0 1 0 1

2 3

0 0 1 0 1

2 2 3

0 1 0

( ) ( )

( ...) ( ...)

( ...) ... ( ...)

( ...) ( ...) ..

( ) ( ...) ..

( ...)(1 ..) [ ( ..)

k k

k i

k k i k

B x b x a x

a a x a a a x

a a a x a a

a a x a a x

a x a a x a a x

a a x x a x x x

  

  

       

        

       

       

         



  

2 3

0 1

( ...) ...] [| | 1]

[ ...]

1 1 1

(1) [ ...] (1) ( )

1 1

a x x x

a x a x

x x x

A x a a x A xA x

x x





     

    

  

   

 

 



((4))продолжение; ((5))Суть

метода траекторий [6]

1 1

n n n n

n m n n n m

С C C C



   

   

1) (комбин) Рассмотрим m сочетаний

с повторениями, составленные из

элементов n+1 типов

1 2

, ,..,

a a a

Число таких сочетаний равно

m m

n n m

C C

 



. Разобьем все эти

сочетания на классы и отнесем к k-

му классу сочетание, в котором k раз

входит элемент

0,k m

Остальные m-k мест могут быть

заняты оставшимися буквами, общее

число которых n. Т.о., в k-ый класс

входят столько сочетаний, сколько

можно составить m-k сочетаний из

элементов n типов. Т.е.

m k

n m k

C C



  



. Общее число

сочетаний

1 1 2

m k m m

n m k n m n m

C C C

 

      



   



. По

свойству [1] следует

1 0

n n n m

C C C

 

  

1 1 1 1

1 2 1

...

m n n n n

n m n m n m n n

C C C C C

   

     

    

. Заменим теперь

( 1) ( )

( ) ( 1)

n n

m m

 

 

получим

1 1

...

n n n n

n m n m n n

C C C C



   

   

Частные случаи:

2 1 1 1

1 2 1

1: ...

m m

n C C C C



    

( 1)! ! 2! 1!

...

2!( 1) ( 1)! 1!1! 1!0!

( 1)

1 2 ...

m n

m m



    

 



    

3 2 2 2

2 1 3 2

2 : ..

m m

n C C C C

 

    

( 2)! ( 1) ! 3! 2!

...

2!( 1)! 2!( 1)! 2!1! 2 !0!

m m

 

   

 

( 1)( 2)

1* 2 2 * 3 ... ( 1)

m m m

m m

 

    

3 3 3

3 2 3

3 : ...

n n n

n C C C C

 

    

( 3)! ( 2)! 4! 3!

...

4!( 1)! 3!( 1)! 3!1! 3!0!

m m

 

   

 

( 1)( 2)( 3)

1 2 3 2 3 4 .. ( 1)( 2)

m m m m

m m m

  



         

С помощью этих формул можно

найти сумму квадратов и сумму

более высоких степеней

натуральных чисел от 0 до n. Для

случая с квадратами используем

n=2.

2 2 2

( 1) 1* 2 2 *3 .. ( 1)

1 2 .. 1 2 ..

m m m m m m

m m

        

       

2 2 2

( 1)

или 1 2 ..

( 1)( 2)

m m

m m m



    

 



2 2 2

( 1)( 2)

или 1 2 ...

( 1) ( 1)(2 1)

2 6

m m m

m m m m m

 

    

  

 

[7]

k k s s

m n n m

C C C









Тождество

Коши.

(комбин) Пусть из группы, состоящей

из m мужчин и n женщин нужно

выбрать k человек. Это можно

сделать

m n



способами. Каждое k

элементное множество можно

классифицировать по числу мужчин.

k – элементное множество,

содержащее s мужчин можно

получит выбирая s мужчин из m.

Тогда женщин в k элементной группе

будет k-s и их можно выбрать

k s



Суммируя получаем

s k s

m n

C C









[8]

0 1 1 0

1 1 1

...

m m m m

n k n k n m k m n k

C C C C C C C



     

   

(траект) Пусть есть сетка А(0,0)-В(n-

m+k+1,m). Рассмотрим все

возможные траектории, являющиеся

ломаными линиями кратчайшей

длины и соединяющими точку A и B.

Пусть каждая горизонтальная линия

0, а вертикальная 1, тогда у каждой

траектории есть соответствие в виде

булевого набора длины n+k+1

(координат точки в сумме). Таких

траекторий

n k

 

. Разобьем

траектории на классы, в классе Vi

попадут все траектории, имеющие

прямую x=k+0,5, в точке

, ее

координаты (k+0,5,i), т.е.

проходящие через B1 и B2. Каждая

траектория в классе Vi, проходящем

через

, разбивается на 3 участка.

1 – ломаная AB1, 2- отрезок B1B2, 3-

ломаная B2B, AB=: A(0;0), Bi(k,i),

0, y 0,x n i 

т.о. у траект. k

горизонт. и i вертикальных отрезков

соответствует набор содержащий

k+i элементов (k нулей, i единиц) =>

выберем траекторию

i n



способами; Участок В1В2 -

единственным способом. Оценим,

B2B: B2 (k+1,i), В(n-m+k+1,m);

( 1, 1), ,x k n m n y i m     

В траектории m-n горизонтальных

отрезков и m-i вертикальных,

соответственно булевой набор

содержит n-i символов.

m i

n i



кол-во

траекторий. Суммируя по классам

получим

i m i m

i k n i n k

C C C



   





[9]

m k n m k

n m n n k

C C C C





(комбин) Сформируем m сочетания в

которых фиксируется

k m

элементов. Возьмем n различных

элементов, выберем из них k

элементов, а из оставшихся n-k

элементов выберем ещё m-k. Так

получим m сочетания

k m k

n n k

C C



способами. Проверим, что при этом

каждое

сочетание получается

способами, а именно выбрать m

элементов из n можно

способами, а зафиксировать k

элементов из m можно

способами. Таким образом, доказано.

[10]

n k

n kC





 



1) (комбин)

Составим список, содержащий по

порядку все подмножества n-

элементного множества х. Этот

список содержит

k –

элементных подмножеств для

1,k n

1 2

- 1 . - , 2 .

n n

C эл мн во C эл

Т.о, его длина или общее число

элементов х выражается суммой

. С

другом стороны, каждый элемент

x X

появляется в списке

n

раз

потому что таково число

подмножеств, содержащих х

(столько же, сколько имеется всех

подмножеств множества х\{x}) Всего

элементов в списке n, поэтому длина

списка равна





2)(ПФ)

(1 )

n k k

x C x



 



Дифференцируем

по х:

1 1

(1 )

n k k

n x kC x

 



 



(х=1

доказано)

[11]

m m k m k

n n n k

C C C







(комбин) Решим следующую задачу:

каким способом можно из n

кандидатов выбрать m депутатов и

из них кого-нибудь наградить.

Можно наградить всех или никого.

Решение: с одной стороны,

депутатов будем выбирать

способами и награждать их будем

способами, с другой стороны,

если число награждаемых депутатов

равно k,

0,k n

, то их можно

выбрать

способами, после чего

остальные m-k депутатов

выбираются

m k

n k



способами.

Суммируя, получаем

k m k

n n k

C C







((5)) Суть метода траекторий.

Пример доказательства одного из

свойств методом траекторий

Свой-во [3](1,8). Метод траекторий

состоит в том, что для

комбинаторной задачи указывается

геометрическая интерпретация,

которая сводит задачу к подсчету

числа путей (траекторий),

обладающих определенным

свойством.

((8)) Разбиение множества, числа

Стирлинга, Белла, свойства,

доказательство 6 свойства

Разбиение n-элементного множества

X на k блоков — это семейство Q =

{B1, …, Bk}, в котором B1 ∪ … ∪ Bk =

X, Bi ∩ Bj = Ø, Bi ≠ Ø, для 1 ≤ i < j ≤ k.

Обозначим множество всех

разбиений множества X на k блоков

через Πk(X), а через Π(X) —

множество всех разбиений. Метод

генерирования разбиений

множества: Каждое разбиение



мн-ва

 

1,.., n

однозн. опр.

разбиение





мн-ва

 

1,.., 1n 

возн из



после удал эл-та n из

соотв. блока и удал образов. пустого

блока если n входила в измененный

блок и наоборот, если дано

разбиение

 

...

B B





мн-ва

 

1,.., 1n 

то легко найти все

разбиения



мн-ва

 

1,.., n

такие

что

 





, т.е.

 

1 2

, ,.., ;

B n B B

 

1 2

, ,.., ;

B n B B

 

1 2

, ,.., .

B B n B

Пример:

Числа Стирлинга первого рода s(n, k)

— это коэффициенты при

последовательных степенях

переменной x в многочлене

[ ]

 

[ ] ,

x s n k x





Свойства: 1)

s(n,k)=0 (k>n) 2) s(n, n) = 1, для n ≥ 0

3) s(n, 0) = 0, для n > 0; 4) s(n, k) =

s(n−1, k−1) + (n−1)s(n−1, k), (0 < k <

n). Число Стирлинга второго рода

S(n, k) — это число разбиений n-

элементного множества на k блоков,

т. е.

S(n, k) = |

(X)|, где множество X

состоит из n элементов. Свойства: 1)

S(0,0)=1 2) S(n,0)=0, (n>0) 3)

S(n,1)=1 (n>0) 4) S(n, n) = 1 5)

S(n,k)=0 (k>n) 6) S(n,k)=S(n-1,k-

1)+kS(n-1,k) Док-во: Рассм мн-во всех

разбиений мн-ва

 

1,...k

на k

блоков. Это мн-во разб на 2 класса:

1) Тех разбиений которые сод

 

качестве 1ноэлементного блока 2)

Тех разб. для которых n явл эл-ом

хотя бы 2хэлем. блока. Мн-во

разбиений первого класса

 

1, 1S n k  

равно числу

разбиения мн-ва

 

1,.. 1n 

на k-1

блок. Мощность второго класса сост.

kS(n-1,k). Т.к.



разб. мн-ва

 

1,.. 1n 

на k блоков в этом классе

соотв k разб. обр. добавлением эл-та

т поочер. л каждому блоку. Число

Белла

— это число всех

разбиений n-элементного

множества:

= |Π(X)|, где |X| = n.

Число Белла можно вычислить как

сумму чисел Стирлинга второго

рода:

( , )

B S n m





Справедлива

также формула Добинского:

e k







Экспоненциальная

производящая функция чисел Белла

имеет вид

n e

n o

x e









1 2

2 3 5

((9))Композиции и разбиения

целых чисел. Задача 1, задача 2,

задача 3.

Задача 1. Сколькими способами

можно записать данное натуральное

число N в виде b1+b2+…+bk=n для

k<=n, bi>0 если порядок слагаемых

является существенным. Числу n

сопоставим линию, состоящую из n

отрезков единичной длины. Линия,

таким образом, разделена n-1 точкой

и композиция получается пометкой

некоторых из них. Элементами

композиции будут расстояния

между смежными точками. Каждая

композиция n соответствует способу

выбора подмножества из n-1 точек.

Чтобы получить композицию из k

частей следует отметить k-1 точку.

Число способов выбора этих точек



. Чтобы найти общее число

композиций просуммируем

1 0 1 1

1 1 1 1

k n

n n n n

k k

C C C C

 

   







    

 



Задача 2. Сколькими способами

можно записать данное натуральное

число N в виде суммы b1+b2+..

+bk=n при фиксированном значении

k<=n, bi>0. Представим число N как

отрезок прямой. Прямая состоит из

N+k отрезков. Расстояние между

последовательно выбранными

точками увеличивается на единицу.

Воспользуемся решением задачи 1.

Задача 3. Имеются марки

достоинством n1,n2,…,nk рублей. Все

числа ni различны и n1<n2<…<nk.

Запас марок не ограничен.

Сколькими способами, наклеивая

марки в ряд, можно оплатить с их

помощью сумму n рублей, если 2

способа следования марок друг за

другом отличающиеся порядком

следования, считаются различными.

Обозначим через F(N) число

способов, которыми можно наклеить

марки для оплаты n рублей. F(0)=1,

т.к. не наклеить ни одной марки мы

можем единственным способом.

F(x)=0, x<n1. Соответственно

F(n1)=1. Для любого N большого

F(N)=F(n-n1)+F(N-n2)+..+F(N-nk).

Теорема. Число разбиений числа n на

k слагаемых равно числу разбиений

числа n с наибольшим слагаемым,

равным k.

Теорема. Перечисляющий

производящей функции для

разбиения без ограничений является

следующее

   

 

2 2 4

( ) 1 .. 1 ..

.. 1

k k

P x x x x x

x x



       

    





Каждый множитель в разбиении

характеризует всевозможные

вклады, имеющие данную величину.

2 3 4

( ) 1 2 3 4 ...

P x p x x x x x





      



Разбиение, все части которых не

превосходят числа k перечисляются

с помощью

( )

P x







Разбиение, в которой все части

нечётные числа

2 1

( )

P x











Разбиение в котором все части

чётные числа

( )

P x





((10))

Разбиения на слагаемые

Необходимо заметить, что

разбиения, отличающиеся только

порядком слагаемых, мы считаем

совпадающими. Назовем (N,K)-

разбиениями все те разбиения числа

N, для которых каждое из слагаемых

не превосходит K. Пусть A(N,K) -

количество таких разбиений. Числа

A(N,K) будем вычислять методом

динамического программирования.

Для вывода рекуррентной формулы

разделим все (N,K)-разбиения на два

класса. В первый попадут разбиения,

в которых есть слагаемые, равные K,

а во второй - все остальные. Ясно,

что количество разбиений во втором

классе равно A(N,K-1). Найдем

количество разбиений в первом.

Заметим, что если из каждого

разбиения этого класса выбросить

одно число K (а их может быть

несколько), то получим все (N-K,K)-

разбиения. Следовательно, верна

следующая формула:A(N, K) = A(N, K-

1) + A(N-K, K)

Перейдем к задаче генерирования

(N,K)-разбиений. Каждое разбиение

единственным образом записывается

в виде последовательности чисел,

расположенных в порядке

невозрастания. Будем порождать

(N,K)-разбиения в

антилексикографическом порядке,

т.е. порядке, обратном Для этого,

согласно предыдущим

рассуждениям, необходимо

сгенерировать сначала все (N-K,K)-

разбиения, приписывая к каждому из

них слева число K, а затем

сгенерировать все (N,K-1)-

разбиения52-3211; 511-31111; 43-

2221; 421-22111; 4111-211111; 331-

1111111;322

Как получить по (N,K)-разбиению

следующее? Каждое разбиение

выглядит таким образом: сначала

идут числа, большие единицы, а

затем - только единицы. Пусть L -

количество единиц в разбиении.

Найдем первое число справа,

большее единицы, и обозначим его

через x. Тогда следующее разбиение

будет таким: все числа до x

останутся теми же самыми, вместо x

будет стоять x-1, а дальше - первое

разбиение числа L+1 на слагаемые,

не превосходящие x-1

((11))Теория Пойа

Пересчет объектов не означает

пересчет их представлений. На

рисунке представлен один объект в

двух представлениях. Если

возникают трудности при точном

определении объектов подлежащих

перечислению, то следует

сконструировать легко

перечислимое множество

представлений для этих объектов, то

есть множество, в котором легко

определить сколько существует

различных представлений. Тогда

задача сводится к определению на

этом множестве отношения

эквивалентности так, чтобы все

представления из этого класса

соответствовали одному и тому же

объекту. Техника подсчета классов

эквивалентностей на множестве

называется теорией Пойа.

Теорема Пойа.

Если дано конечное множество D

называемое областью определения и

конечное множество R называемое

областью значений, а также группа

подстановок G на D, то определим

{ | : }S f f D R 

. Далее

определим отношение

эквивалентности гамма на S,

индуцируемое G, то есть fгаммаg

если и только если существует

подстановка P

такая, что f=gП.

Определим цикловой индекс

| |

1 2

1 2 | |

l ( )

l ( ) l ( )

1 2 | |

( , ,..., )

* ...

161

G D

П П

П G

P x x x

x x x







Теорема Пойа. Число классов

эквивалентностей относительно

гамма равно P

(|R|,..,|R|), где

мощность R это число мощностей R.

Лемма.

Пусть дано конечное множество S и

группа G’ подстановок на множестве

S. Определим на S отношение

эквивалентностей гамма,

порождаемое группой G’, fгаммаg

если и только если G’ существует,

подстановка П такая, что f=П(g).

Определим П(П) как число элементов

множества S, инвариантных

относительно подстановки П (f из S

инвариантен относительно

подстановки П, если и только если

П(f)=f.

Лемма Бернсайля. Число классов

эквивалентностей относительно

гамма равно

( )

П G

I П



