Шпора по эконометрике

Подождите немного. Документ загружается.

1. Понятие о функциональной, статистической и корреляционной связях.

Различают два типа связей между различными явлениями и их признаками: функциональную или жестко детерминированную, с

одной стороны, и статистическую или стохастически детерминированную- с другой. Строго определить различие этих типов

связи можно тогда, когда они получают математическую формулировку. Для простоты будем говорить о связи двух явлений или

двух признаков, математически отображаемой в форме уравнения связи двух переменных.

Если с изменением значения одной из переменных вторая изменяется строго определенным образом, т.е. значению одной

переменной обязательно соответствует одно или несколько точно заданных значений другой переменной, связь между ними

является функциональной.

Нередко говорят о строгом соответствии лишь одного значения второй из переменных каждому значению первой из них, но это

неверно. Например, связь между у и х является строго функциональной, если , но значению х = 4 соответствует не одно,

а два значения: у1 = +2; у2 = - 2. Уравнения более высоких степеней могут иметь несколько корней, связь, разумеется, остается

функциональной.

Функциональная связь двух величин возможна лишь при условии, что вторая из них зависит только от первой и ни от чего более.

В реальной природе (и тем более в обществе) таких связей нет; они являются лишь абстракциями, полезными и необходимыми

при анализе явлений, но упрощающими реальность. Функциональная зависимость данной величины у от многих факторов х1, х2,

..., хn возможна только в том случае, если величина y всегда зависит только от перечисленного набора факторов x1, х2 ..., хk и ни

от чего более. Между тем все явления и процессы безграничного реального мира связаны между собой, и нет такого конечного

числа переменных k, которые абсолютно полно определяли бы собою зависимую величину y. Следовательно, множественная

функциональная зависимость переменных есть тоже абстракция, упрощающая реальность.

2. Основные задачи прикладного корреляционно-регрессионного анализа.

Основными задачами корреляционного анализа являются оценка силы связи и проверка статистических гипотез о наличии и силе

корреляционной связи. Не все факторы, влияющие на экономические процессы, являются случайными величинами, поэтому при

анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи

называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом.

Использование возможностей современной вычислительной техники, оснащенной пакетами программ машинной обработки

статистической информации на ЭВМ, делает практически осуществимым оперативное решение задач изучения взаимосвязи

показателей биржевых ставок методами корреляционно-регрессионного анализа.

При машинной обработке исходной информации на ЭВМ, оснащенных пакетами стандартных программ ведения анализов,

вычисление параметров применяемых математических функций является быстро выполняемой счетной операцией.

3. Уравнение регрессии, его смысл и назначение. Выбор типа матем-й функции при построении уравнения регрессии.

Смысл регрессионного анализа – построение функциональных зависимостей между двумя группами переменных величин Х

, Х

… Х

и Y. При этом речь идет о влиянии переменных Х (это будут аргументы функций) на значения переменной Y (значение

функции). Переменные Х мы будем называть факторами, а Y – откликом.

Сегодня мы разберем наиболее простой случай – установление зависимости одного отклика y от одного фактора х. Такой случай

называется парной (простой) регрессией.

Построение модели

Исходные данные: заранее известные (экспериментальные, наблюденные) значения фактора х

– экзогенная переменная и

соответствующие им значения отклика y

, (i = 1,…,n) - эндогенная переменная;

Активный и пассивный эксперимент.

Выборочные характеристики – позволяют кратко охарактеризовать выборку, т. е., получить ее модель, хотя и очень грубую:

а) среднее арифметическое:





Среднее арифметическое – это «центр», вокруг которого колеблются значения случайной величины.

Основные этапы построения эконометрических моделей

На первом постановочном этапе построения эконометрической модели формируются цели моделирования, определяется набор

участвующих в модели факторов, т.е. устанавливается, какие из переменных будут рассматриваться как экзогенные, а какие как

эндогенные и лаговые.

Пусть У ={у1 у2 …уm}, множество эндогенных переменных ; Х = {х1 х2 …хm} – множество экзогенных переменных.

Задачей экзогенного моделирования является получение каждой эндогенной переменной от совокупности экзогенных

переменных и возможно от части эндогенных.

y1 = f (x1 … xk у2 … уm)

При этом зависимые переменных лаговые.

На 1 ом этапе осуществляется анализ экономической сущности изучаемой модели.

На 3 ем этапе выбор общего вида модели: парная, множественная; сколько должно войти факторов; линейная не линейная; а так

же определение коэффициентов функции f.

4 ый этап отбор необходимой статистической информации и предварительный анализ данных.

5 ый этап – идентификация модели, т.е. стат анализ модели, стат оценка независимых параметров модели. Наиболее часто для

оценки (нахождения) параметров модели применяют метод наименьших квадратов (МНК)

6 ой этап – сопоставление реальных и модельных значений. Иначе оценка адекватности и точности модели.

По точной и адекватной модели осуществляется прогнозирование.

4. Парной регрессией называется уравнение связи двух переменных у и х

Вида y = f (x),

где у – зависимая переменная (результативный признак);

х – независимая, объясняющая переменная (признак-фактор).

Различают линейные и нелинейные регрессии.

Метод наименьших квадратов МНК

Для оценки параметров регрессий, линейных по этим параметрам, используется метод наименьших квадратов (МНК). МНК

позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного

признака у от теоретических значений ŷx при тех же значениях фактора x минимальна, т. е.

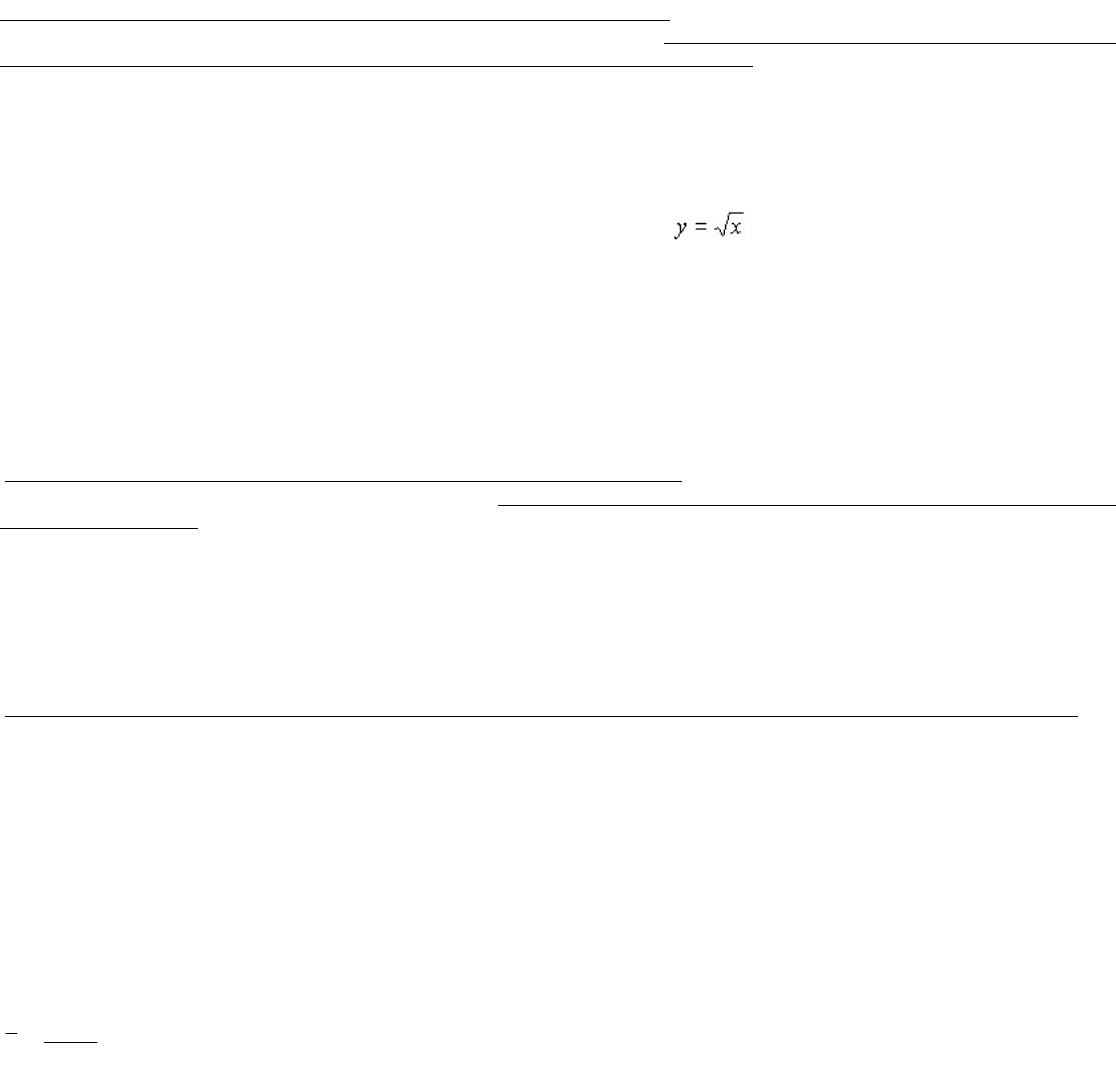
5. Нелинейные регрессии делятся на два класса : регрессии, нелинейные относительно иключенных в анализ объясняющих

переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.

Примеры регрессий, нелинейных по объясняющим переменным, но линейных по оцениваемым параметрам:

Нелинейные модели регрессии и их линеаризация

При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также

определяются по МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным. Так,

рассматривая степенную функцию

xxxay  

мы преобразовываем ее в линейный вид:

xbxbxbay lglglglg

2211

 

где переменные выражены в логарифмах.

Далее обработка МНК та же: строится система нормальных уравнений и определяются неизвестные параметры.

Потенцируя значение

alg

, находим параметр a и соответственно общий вид уравнения степенной функции.

Вообще говоря, нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее

параметров. Эта оценка определяется, как и в линейной регрессии, МНК. Так, в двухфакторном уравнении нелинейной регрессии

1322110

xaxaxaxaay 

может быть проведена линеаризация, введением в него новых переменных

, xxxx 

. В результате получается

четырехфактороное уравнение линейной регрессии

443322110

xaxaxaxaay 

6. Оценка тесноты связи

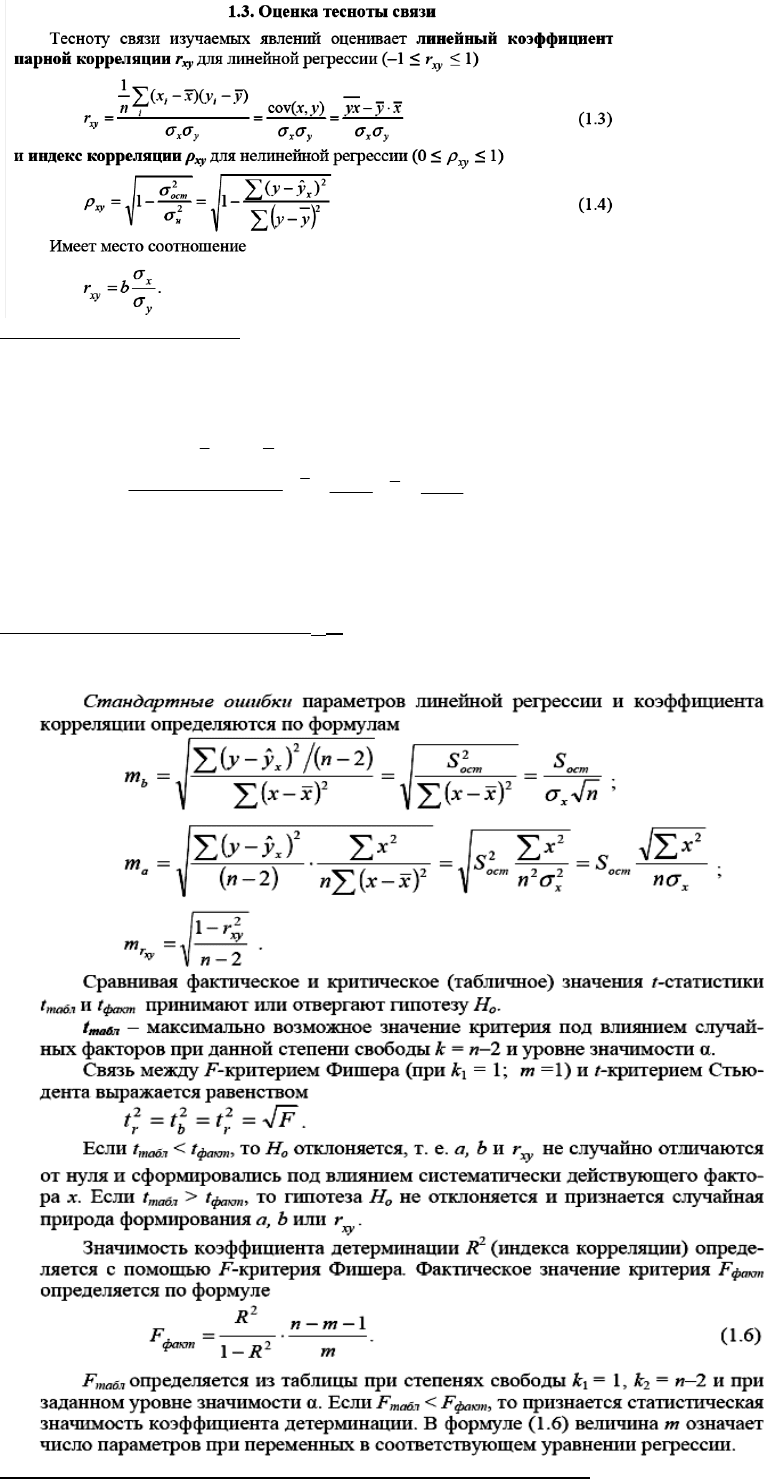
Коэффициент ковариации

(у) - Т.е. получим корреляционную зависимость.

Наличие корреляционной зависимости не может ответить на вопрос о причине связи. Корреляция устанавливает лишь меру этой

связи, т.е. меру согласованного варьирования.

Меру взаимосвязи м\у 2 мя переменными можно найти с помощью ковариации.

))((

)cov(











yyxx











Величина показателя ковариации зависит от единиц в γ измеряется переменная. Поэтому для оценки степени согласованного

варьирования используют коэффициент корреляции – безразмерную характеристику имеющую определенный пределы

варьирования..

8. Коэффициент детерминации (r

) – характеризует долю дисперсии результативного признака y, объясняемую дисперсией,

в общей дисперсии результативного признака. Чем ближе r

к 1, тем качественнее регрессионная модель, то есть исходная

модель хорошо аппроксимирует исходные данные.

9. Оценка статистической значимости пок. коррел. Стьюдента.

10 Оценка статистической значимости пок. Коррел. Фишера.

11. Понятие о множ. регрессии.

Линейная модель множественной регрессии

ppx

xbxbxbay  

2211

12. Определение параметров уравнения множественной регрессии методам наименьших квадратов

13. Стандартизованные коэфф. Регрессии, их интерпретация.

14. Парные и частные коэффициенты корелляции.

Следует отметить, что величины

называются парными коэффициентами корреляции и определяются по

формулам

xyyx







jiji

xxxx







15. Множественный коэффициент корелляции, множ. Коэфф. Детерминации.

16. Оценка надежности показателей корелляции (множественная регрессия)

17. Оценка качества модели множественной регрессии Фишера

18. Оценка качества модели множественной регрессии Стьюдента

19.

20. Гомоскедастичность

Гомоскедастичность остатков означает, что дисперсия каждого отклонения одинакова для всех значений x. Если это

условие не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля

корреляции (смотри рисунок).

Т.к. дисперсия характеризует отклонение то из рисунков видно, что в первом случае дисперсия остатков растет по мере

увеличения x, а во втором – дисперсия остатков достигает максимальной величины при средних значениях величины x и

уменьшается при минимальных и максимальных значениях x. Наличие гетероскедастичности будет сказываться на уменьшении

эффективности оценок параметров уравнения регрессии. Наличие гомоскедастичности или гетероскедастичности можно

определять также по графику зависимости остатков от теоретических значений

Автокорреляция

Влияние фактора времени будет выражено в корреляционной зависимости между значениями остатков Еt за текущий и

предыдущие моменты времени, которая получила название «автокорреляция в остатках».

Автокорреляция в остатках есть нарушение одной из основных предпосылок МНК – предпосылки о случайности остатков,

полученных по уравнению регрессии. Один из возможных путей решения этой проблемы состоит в применении к оценке

параметров модели обобщенного МНК. При построении уравнения множественной регрессии по временным рядам данных,

помимо двух вышеназванных проблем, возникает также проблема мультиколлинеарности факторов, входящих в уравнение

регрессии, в случае если эти факторы содержат тенденцию.

Отсутствие автокорреляции остатков

Под автокорреляцией остатков понимают зависимость распределения значений остатков



друг от друга.

Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений.

Оценить эту зависимость можно вычислив коэффициент корреляции между этими остатками по формуле, аналогичной (6)

jiji











. (10)

Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированны.

21. Специфика временных рядов как источника данных в эконометрическом моделировании.

Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются

моделями временных рядов.

Временной ряд – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.

Применение традиционных методов корреляционно-регрессионного анализа для изучения причинно следственных зависимостей

переменных, представленных в форме временных рядов, может привести к ряду серьезных проблем, возникающих как на этапе

построения, так и на этапе анализа эконометрических моделей. В первую очередь эти проблемы связаны со спецификой

временных рядов как источника данных в эконометрическом моделировании.

Предполагается, что в общем случае каждый уровень временного ряда содержит три основные компоненты: тенденцию (Т),

циклические или сезонные колебания (S) и случайную компоненту (E).

Если временные ряды содержат сезонные или циклические колебания, то перед проведением дальнейшего исследования

взаимосвязи необходимо устранить сезонную или циклическую компоненту из уровней каждого ряда, поскольку ее наличие

приведет к завышению истинных показателей силы и связи

изучаемых временных рядов в случае, если оба ряда содержат циклические колебания одинаковой периодичности, либо к

занижению этих показателей в случае, если сезонные или циклические колебания содержит только один из рядов или

периодичность колебаний в рассматриваемых временных рядах различна.

Устранение сезонной компоненты из уровней временных рядов можно проводить в соответствии с методикой построения

аддитивной и мультипликативной моделей. Если рассматриваемые временные ряды имеют тенденцию, коэффициент корреляции

по абсолютной величине будет высоким, что в данном случае есть результат того, что х и у зависят от времени, или содержат

тенденцию. Для того чтобы получить коэффициенты корреляции, характеризующие причинно следственную связь между

изучаемыми рядами, следует избавиться от так называемой ложной корреляции, вызванной наличием тенденции в каждом ряде.

Влияние фактора времени будет выражено в корреляционной зависимости между значениями остатков et за текущий и

предыдущие моменты времени, которая получила название «автокорреляция в остатках».

регрессии, в случае если эти факторы содержат тенденцию.

22. Аналитическое выравнивание временных рядов. Оценка параметров уравнения тренда.

Аналитическое выравнивание временного ряда – способ моделирования тенденции временного ряда: построение

аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда.

23. Автокорреляция в остатках, ее измерение и интерпретация. Критерий Дарбина-Уотсона в оценке качества

трендового уравнения регрессии.