Шпаргалка по программированию на Турбо Паскаль
Подождите немного. Документ загружается.

сравнивается с результатом, полученном на предыдущем шаге. Вычисления повторяются
в цикле, пока разница между результатами не станет меньше e.
20. Численные методы решения нелинейных уравнений.
Общие принципы.
При решении инженерных задач встречаются алгебраические и трансцендентные
уравнения, решение которых может представлять собой самостоятельную задачу или быть
составной частью более сложных задач. В обоих случаях применение численного метода
позволяет быстро и эффективно добиться решения задачи.
Алгебраические уравнения имеют n решений, трансцендентные – неопределённое число
решений. Уравнения, содержащие только суммы целых степеней x, называются
алгебраическими. Их общий вид
a
n
x
n
+a
n-1
x
n-1
+...+a
1
x+a
0
=0
Нелинейные уравнения, содержащие тригонометрические функции или другие
специальные функции, например, exp, называются трансцендентными.
Если отсутствует аналитическое решение нелинейного уравнения или оно очень сложно,
применяют численные методы, в которых, как правило, применяются итерационные
алгоритмы. В итерационных методах задаётся процедура решения в виде многократного
применения некоторого алгоритма. Полученное решение всегда является приближённым,
хотя может быть сколь угодно близким к точному.
Пусть на отрезке [a,b] дана непрерывная функция y=f(x), причем значения f(a) и f(b)
имеют разные знаки. Тогда абсцисса точки пересечения графика функции y=f(x) с осью X
будет корнем уравнения f(x)=0. Другими словами, требуется найти такое значение x, при
котором значение функции f(x) будет равно нулю.
Численными методами значение корня определяется с погрешностью, не превосходящей
данного положительного, достаточно малого числа ε. Иначе говоря, если v – истинное
значение корня, при котором f(v)=0, то требуется определить такое число w, при котором
a=<ε.
Первый этап решения состоит в отыскании области существования корня, т.е. отрезков на
оси абсцисс, в концах которых функция имеет разные знаки. Для этого вычисляются
значения функции в точках, расположенных через равные интервалы на оси x. Это
делается до тех пор, пока не будут найдены два последовательных значения функции f(x
n
)
и f(x
n+1
), имеющих противоположные знаки, т.е. f(x
n
)*f(
n+1
)<0. Таким образом, при a= x
n
,
b=
n+1
, уточнение корней будет производиться на отрезке [a,b]. Для решения этой задачи
применяются методы половинного деления, касательных (Ньютона), хорд и секущих.
21. Численные методы решения нелинейных
уравнений.
Метод половинного деления.
Алгоритм метода состоит из следующих операций. Отрезок [a,b] делят пополам точкой c,
c=(a+b)/2, и находят значение функции в точке с. Если f(c)=0, то корень уравнения
соответствует точке c. Если f(c)≠0, то можно сузить диапазон поиска корня: перейти от
отрезка [a,b] к отрезку [a,c] или [c,b] в зависимости от знака f(c). Если f(a)*f(c)<0, то корень
находится на отрезке [a,c], и точку с будем считать точкой b; а если f(a)*f(c)>0, то корень
находится на отрезке [c,b], и точку с будем считать точкой a.
Каждый такой шаг уменьшает в два раза интервал, в котором находится корень
уравнения f(x)=0. После нескольких шагов получится отрезок, длина которого будет
меньше или равна числу ε, т.е. |a-b|=<ε. Любая точка такого отрезка, например, один
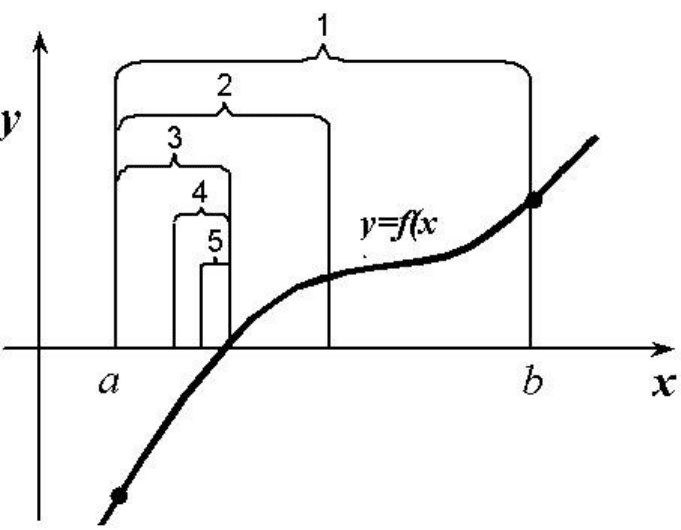
из его концов, подходит в качестве решения поставленной задачи. На рисунке
показано несколько этапов применения алгоритма. Здесь 1…5 – интервалы уточнения
корней на 1..5 шаге алгоритма.
Пример: Найти с точностью ε=0,001 на отрезке [-2,1] корень уравнения x
3
+x
2
+x+1=0.
Приведём текст программы, которая решает эту задачу методом половинного деления.
Результат выводится на экран, и, по желанию пользователя, на принтер.
Program Popolam;
Uses Crt, Printer;
Var
a,b,c,eps,a0,b0:real;
k:integer;
ch:char;
Function f(x:real):real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Begin
ClrScr;
Writeln(' Решение уравнения методом половинного деления ');
{ Ввод исходных данных }
a:=-2; b:=1; eps:=0.001;
a0:=a; b0:=b; { запоминаем исходные данные }
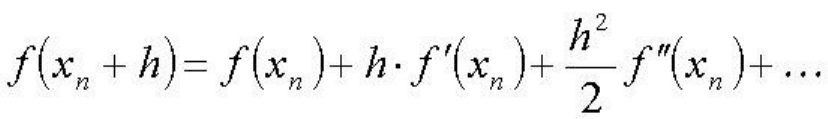
{ Начинаем расчет }
k:=0; { Счетчик повторений }
While abs(b-a)>=eps do
begin
k:=k+1;
c:=(a+b)/2;
if f(a)*f(c)<=0 then b:=c
else a:=c;
end;
Writeln(' Уравнение x^3+x^2+x+1=0 на отрезке [',a0:4:1, ',',
b0:4:1, '] имеет корень x = ', c:10:8);
Writeln(' f(x) = ',f(c):10:8);
Writeln('Точность ',eps:10:8, ' достигнута за ',
k,' итераций');
Write(' Печатать результаты на принтере? (Y/N)');
Repeat
ch:=ReadKey;
ch:= UpCase(ch);
Until (ch='Y') or (ch='N');
if ch='Y' then
begin
Writeln(lst,'Решение уравнения методом половинного деления');
Writeln(lst,' Уравнение x^3+x^2+x+1=0 на отрезке [',
a0:4:1, ',', b0:4:1, '] имеет корень x = ', c:10:8);
Writeln(lst,' f(x) = ',f(c):10:8);
Writeln(lst,' Точность ',eps:10:8, ' достигнута за ',
k,' итераций');
Writeln('Печать выполнена. Нажмите ENTER ');
Readln;
end;
End.
22. Численные методы решения нелинейных уравнений.
Метод Ньютона (метод касательных).
В отличие от метода половинного деления, для определения интервала, в котором
заключён корень, не требуется находить значения функции с противоположными знаками.
Вместо интерполяции по двум значениям функции, в методе Ньютона делается
экстраполяция с помощью касательной к кривой в данной точке. В основе метода лежит
разложение функции f(x) в ряд Тейлора:
Члены ряда, содержащие h во второй и более высоких степенях, отбрасываются;
используется соотношение x
n
+h=x
n+1
. Предполагается, что переход от x
n
к x
n+1
приближает
значение функции к нулю так, что f(x
n
+h)=0. Тогда x
n+1
=x
n
-f(x
n
)/f'(x
n
).
Значение x
n+1
соответствует точке, в которой касательная к кривой в точке x
n
пересекает
ось x. Так как кривая f(x) отлична от прямой, то значение функции f(xn+1) не будет в
точности равно нулю. Поэтому вся процедура пoвторяется, причём вместо x
n
используется
x
n+1
. Счет прекращается, когда разница между x
n
и x
n+1
будет меньше или равна числу ε,
т.е. |x
n
-x
n+1
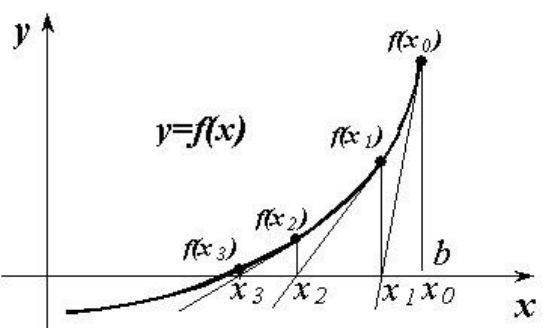
|=<ε. На рисунке процесс решения уравнения методом Ньютона показан
графически.
Пример: Приведём фрагменты текста программы, которая решает задачу из предыдущего
примера (раздел 21) методом касательных. Ввод и вывод результатов подробно разобран
выше.
Program Kasat;
Uses Crt, Printer;
Var
a,b,t,x,eps:real;
Function f(x:real):real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Function f1(x:real):real;
begin
{ Здесь приводим выражение для производной функции }
f:=3*x*x+2*x+1;
end;
Begin
ClrScr;
Writeln(' Решение уравнения методом касательных');
{ Ввод исходных данных }
a:=-2; b:=1; eps:=0.001;
{ Начинаем расчет }
x:=a;
Repeat
t:=f(x)/f1(x);
x:=x-t;
Until abs(t)<=eps;
Writeln(' Уравнение имеет корень x = ', x:10:8);
Readln;
End.
Метод Ньютона требует меньшего числа повторений, чем метод половинного деления.
Недостатки метода – необходимость дифференцирования функции f(x), и f(x) должно
быть не равно нулю.
23. Численные методы решения нелинейных уравнений.
Метод хорд (метод ложного положения).
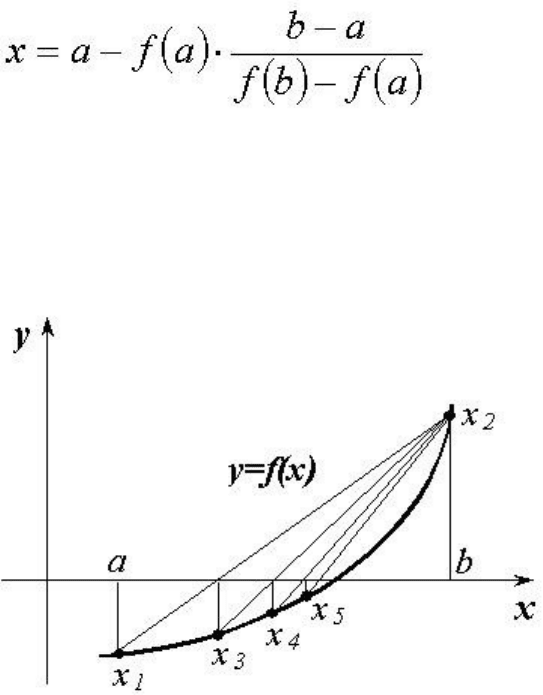
В основе метода лежит линейная интерполяция по двум значениям функции f(x),
имеющим противоположные знаки. Через точки, соединяющие значения функции f(a) и
f(b) на концах отрезка [a,b], проводят прямую, которая пересекает ось x в точке
Значение функции f(x) сравнивается со значениями функций f(a) и f(b) и в дальнейшем
используется вместо того из них, с которым оно совпадает по знаку. Если значение f(x)
недостаточно близко к нулю, то вся процедура повторяется до тех пор, пока не будет
достигнута необходимая степень сходимости ε. На рисунке процесс решения показан
графически.
Пример: Приведём фрагменты текста программы, которая решает задачу из предыдущего
примера (раздел 22) методом хорд.
Program Horda;
Uses Crt;
Var
a,b,t,x,eps:real;
Function f(x:real):real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Begin
ClrScr;
Writeln(' Решение уравнения методом хорд');
{ Ввод исходных данных }
a:=-2; b:=1; eps:=0.001;
{ Начинаем расчет }
Repeat
x:=a-f(a)*(b-a)/(f(b)-f(a));
if f(a)*f(x)<=0 then b:=x
else a:=x;
Until abs(f(x))<=eps;
Writeln(' Уравнение имеет корень x = ', x:10:8);
Readln;
End.

24. Численные методы решения обыкновенных
дифференциальных уравнений. Общие принципы.
Дифференциальными называются уравнения, содержащие одну или несколько
производных. Поскольку большая часть законов физики формулируется именно в виде
дифференциальных уравнений, то инженеру приходится сталкиваться с ними. Лишь
немногие из них удаётся решить без помощи компьютера. Поскольку большая часть
законов физики формулируется именно в виде дифференциальных уравнений, то
инженеру приходится сталкиваться с ними. Поэтому численные методы решения
дифференциальных уравнений играют важную роль в практике инженерных расчётов.
Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения
зависимой переменной и (или) её производных при некоторых значениях независимой
переменной. Если дополнительные условия задаются при одном значении независимой
переменной, то такая задача называется задачей с начальными условиями, или задачей
Коши. Если же условия задаются при двух или более значениях независимой переменной,
то такая задача называется краевой. В задаче Коши дополнительные условия называются
начальными, а в краевой задача – граничными.
Рассмотрим способы решения задачи Коши, которая формулируется следующим образом.
Пусть дано дифференциальное уравнение и начальное условие y(x
0
)=y
0
. Требуется найти
функцию y(x), удовлетворяющую как указанному уравнению, так и начальному условию.
Искомая функция выражается в табличном виде
x
0
x
1
x
2
x
3
... x
n
y
0
y
1
y
2
y
3
... y
n
Значения x вычисляются, через малое приращение h, h=x
0
-x
1
=x
2
-x
1
. Обычно численное
решение этой задачи получают, вычисляя сначала значение производной, а затем, задавая
малое приращение для x, переходят к новой точке x
1
=x
0
+h. Положение новой точки
определяется по наклону кривой, вычисленному с помощью дифференциального
уравнения. Таким образом, график численного решения представляет собой
последовательность коротких прямолинейных отрезков, которыми аппроксимируется
истинная кривая y=f(x). Сам численный метод определяет порядок действий при переходе
от данной точки кривой к следующей. На рисунке показано графическое представление
численного решения задачи Коши. Здесь 1 – точное решение; 2 – решение, полученное
численным методом.
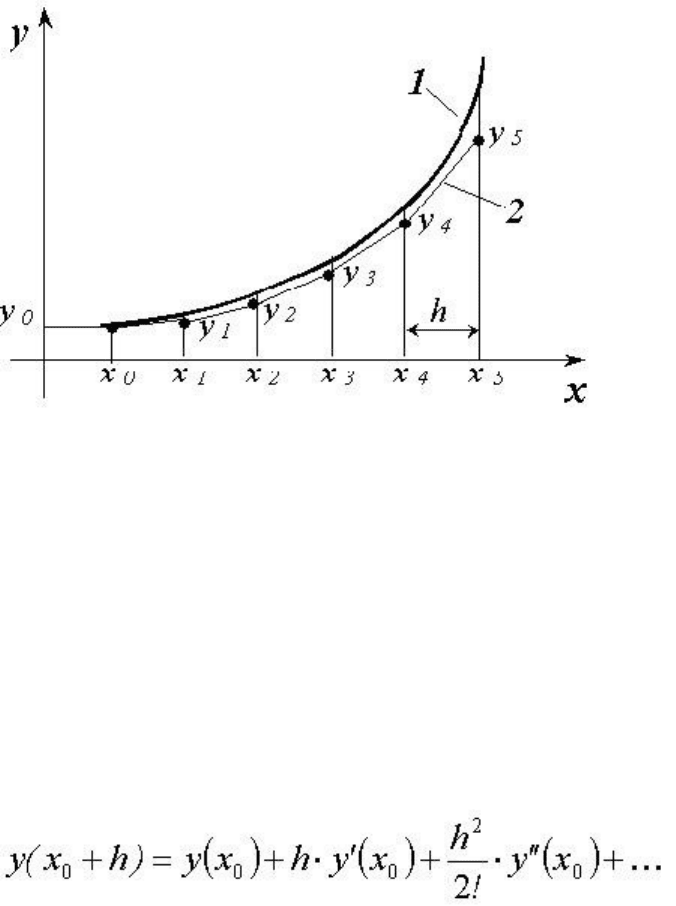
Наиболее простыми из методов решения задачи Коши являются методы Эйлера и Рунге-
Кутта. Они используются для решения дифференциальных уравнений первого порядка
вида y`=f(x,y), где y`=dy/dx, при начальном условии y(x
0
)=y
0
.
25. Численные методы решения обыкновенных
дифференциальных уравнений. Метод Эйлера.
Это простейший метод решения задачи Коши, позволяющий решить дифференциальное
уравнение первого порядка. Его точность невелика, поэтому на практике им пользуются
редко. Однако, на основе этого метода легче понять алгоритм других, более эффективных
методов. Метод Эйлера основан на разложении функции y в ряд Тейлора в окрестности x
0
:
Если h мало, то члены, содержащие производные второго и более высоких порядков,
можно отбросить. Тогда
y(x
0
+h)=y(x
0
)+h*y`(x
0
)
y’(x
0
) находим из дифференциального уравнения, подставив в него начальное условие.
Таким образом, можно получить приближённое значение y при малом смещении h от
начальной точки x(x
0
). Этот процесс можно продолжить, используя следующую
рекуррентную формулу
yi+1=yi + h*f(xi,yi), i=1,2,…
Графически метод Эйлера показан на рисунке. Ошибка метода имеет порядок h2.
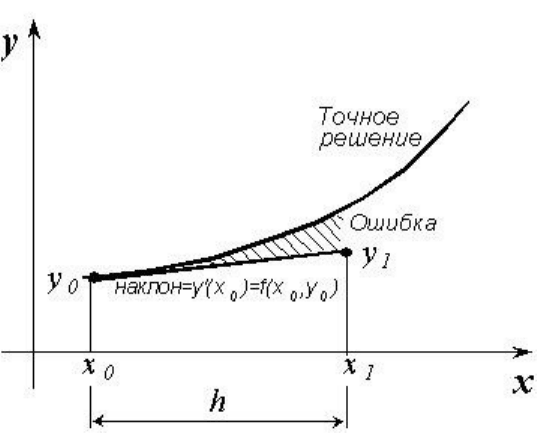
Пример: Составим программу для решения дифференциального уравнения y'=2x
2
+2y при
начальном условии y(0)=1; 0 =< x =< 1 и h=0,1.
Program Euler;
Uses Crt;
Var
xn,xk,yn,h,x,y:real;
i:integer;
Function f(x,y:real):real;
begin
{Здесь приводим выражение для вычисления функции f(x,y) }
f:=2*x*x+2*y;
end;
Begin
ClrScr;
Writeln(' Решение дифференциального уравнения ');
Writeln(' dy/dx=2x^2+2y методом Эйлера ');
{ Ввод исходных данных }
xn:=0; yn:=1; xk:=1; h:=0.1;
{ Выводим шапку таблицы и первую точку }
Writeln('--------------------');
Writeln('| № | x | y |');
Writeln('--------------------');
{ Начинаем расчет }
x:=xn; y:=yn; i:=1;
Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |');
repeat
y:=y+h*f(x,y);
Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |');
x:=x+h;
i:=i+1;
until x>xk;
Writeln('--------------------');
Readln;
End.
26. Численные методы решения обыкновенных
дифференциальных уравнений. Модифицированный
метод Эйлера.
Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию
производной. Это можно сделать, например, используя среднее значение производной в
начале и в конце интервала. В модифицированном методе Эйлера сначала по методу
Эйлера вычисляется значение функции в следующей точке:
y*
i+1
= y
i
+ h*f(x
i
,y
i
)
Оно используется для вычисления приближённого значения производной в конце
интервала f(
i+1
, y*
i+1
). Вычислив среднее между этим значением производной и её
значением в начале интервала, найдём более точное значение y
i+1
:
y
i+1
= y
i
+ h/2*[f(x
i
,y
i
) + f(x
i+1
, y*
i+1
)] .
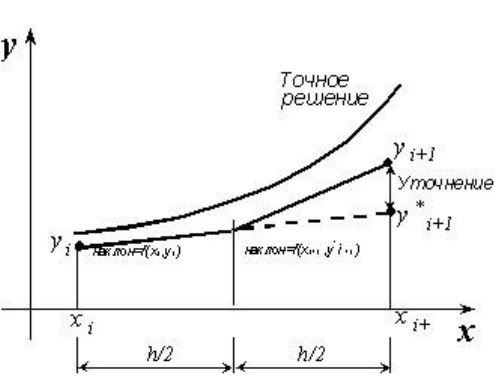
Принцип метода проиллюстрирован на рисунке. Для получения новой точки в нём
требуется информация о двух других точках – предыдущей и промежуточной.
Ошибка этого метода на каждом шаге имеет порядок h
2
.
Пример: Разработать, сохранить и выполнить программу для решения
дифференциального уравнения из предыдущего примера (раздел 25) модифицированным
методом Эйлера. При выполнении расчетов использовать хранение результатов в
массивах.
Program ModEuler;
Uses Crt;
Var
xn,xk,yn,yw,h:real;
i,n:integer;
x,y:array [1..20] of real;
Function f(x,y:real):real;
begin
f:=2*x*x+2*y;
end;
Begin
ClrScr;
Writeln(' Решение дифференциального уравнения ');
Writeln(' dy/dx=2x^2+2y модифицированным методом Эйлера ');
xn:=0; yn:=1; xk:=1; h:=0.1;
x[1]:=xn; y[1]:=yn; i:=1;
repeat
yw:=y[i]+h*f(x[i],y[i]);
y[i+1]:=y[i]+h/2*(f(x[i],y[i])+f(x[i]+h,yw));
x[i+1]:=x[i]+h;
i:=i+1;
until x[i]>xk;
n:=i;
{ Выводим результаты }
Writeln('--------------------');
Writeln('| № | x | y |');
Writeln('--------------------');
for i:= 1 to n do
Writeln('|', i:2, ' |', x[i]:5:2, ' |', y[i]:7:4, ' |');
Writeln('--------------------');
Readln;
End.
27. Численные методы решения обыкновенных
дифференциальных уравнений. Метод Рунге-Кутта.
Для повышения точности вычисления значений функции требуется проведение
дополнительных вычислений внутри интервала h, то есть между x
i
и x
i+1
. Метод Рунге-
Кутта даёт набор формул для расчёта координат внутренних точек, требуемых для
достижения точности, то есть ошибки на каждом шаге, порядка h
4
. Расчёты при
использовании этого метода производятся по формуле
y
i+1
=y
i
+(k
0
+2k
1
+2k
2
+k
3
)/6
Здесь k
0
=h*f(x
i
,y
i
),
k
1
=h*f(x
i
+h/2, y
i
+k
0
/2),
k
2
=h*f(x
i
+h/2, y
i
+k
1
/2),
k3=h*f(x
i
+h, y
i
+k
2
)
Метод Эйлера и его модификация по существу являются методами Рунге-Кутта первого и
второго порядка соответственно. По сравнению с ними метод Рунге-Кутта обеспечивает
более высокую точность, что позволяет увеличить шаг интегрирования h. Допустимая
погрешность на шаге определяет его максимальную величину.
Пример: Приведём фрагмент программы для решения дифференциального уравнения из
предыдущего примера (раздел 26) методом Рунге-Кутта.
Program Runge;
Uses Crt;
Var
xn,xk,yn,h,k0,k1,k2,k3:real;
i,n:integer;
x,y:array [1..20] of real;
Function f(x,y:real):real;
begin
f:=2*x*x+2*y;
end;
Begin
ClrScr;
Writeln(' Решение дифференциального уравнения ');
Writeln(' dy/dx=2x^2+2y методом Рунге-Кутта ');
