Шипулин В.Д. Основные принципы геоинформационных систем. Уч. пособие
Подождите немного. Документ загружается.

121
Таблица 2.4.5 – Резюме представления географических объектов
растровыми моделями [29].
Фокус модели Триангуляционные данные ориентированы
на моделирование непрерывных явлений и
изображений земной поверхности.
Источники данных Материалы аэрофотосъемки, космической
съемки
сбор GPS определений,
конвертирование из триангуляционных
данных,
растеризация векторных данных,
Сканирование фотографий и чертежей.
Хранение
пространственных
данных
От координат нижнего левого угла растра
и высоты, ширины ячейки, каждая ячейка
локализована позицией ее ряда и колонки.
Представление
пространственных
объектов
Точечные пространственные объекты
представляются одной ячейкой. Линейные
пространственные объекты
представляются цепочкой смежных ячеек с
одинаковым значением. Полигональные
пространственные объекты
представляются регионами ячеек с
одинаковым значением.
Топологические
отношения
Смежные ячейки могут быстро
локализованы приращением и вычитанием
значений рядов и колонок.
Геопространственный
анализ
Пространственное совпадение, анализ
близости, анализ поверхности, дисперсия,
путь наименьших затрат.
Картографическая
продукция
Растровые данные являются лучшими для
презентации изображений и непрерывных
явлений с постепенным варьированием
атрибутов. Они не совсем подходят для
вычерчивания точечных и линейных
пространственных объектов.
122
2.4.8 Контрольные вопросы и задания для самостоятельной
работы
1) В чем состоит сущность растровых моделей географических
объектов?
2) Как представляются дискретные географические объекты в
растровых моделях?
3) Дайте определение поверхности.
4) Как представляются непрерывные явления растровыми и
сеточными моделями?
5) В чем состоят преимущества и недостатки растровых
моделей?
6) Чем определяется разрешение растра?
7) Как определяются координаты ячеек растра в системе
координат растра и геодезической системе координат?
8) Чем определяется экстент региона, топология ячеек растра?
9) Опишите известные вам цветовые модели.
10) Что есть зонирование? Как можно использовать таблицу
атрибутов растра для операций зонирования?
11) Опишите способ полного представления и способ
последовательного кодирования для хранения растровых
данных.
12) Опишите сущность метода группового кодирования и
методов, основанных на порядке сканирования для сжатия
растровых данных.
13) Опишите сущность метода квадротомического дерева для
сжатия растровых данных.
14) Приведите краткую характеристику форматов хранения
растровых данных.
15) Что представляет собой файл привязки растровых данных?
16) Приведите обобщенную характеристику представления
географических объектов растровыми моделями.
123
Раздел 2.5
ТРИАНГУЛЯЦИОННЫЕ МОДЕЛИ
ГЕОГРАФИЧЕСКИХ ОБЪЕКТОВ
2.5.1 Определение модели TIN
Модель TIN (Triangulation Irregular Network - триангуляционная
нерегулярная сеть) географических объектов – модель поверхности в
виде сети смежных не пересекающихся треугольных граней,
определенная по узлам и ребрам, которые покрывают поверхность.
Слова в названии модели означают следующее:
Triangulation (Триангуляционная) – указывает способ построения
оптимизированного набора треугольников по набору точек;
Irregular (Нерегулярная) – точки могут быть взяты с переменной
плотностью для моделирования участков поверхности, где рельеф
резко меняется;
Network (Сеть) – отражает топологическую структуру.
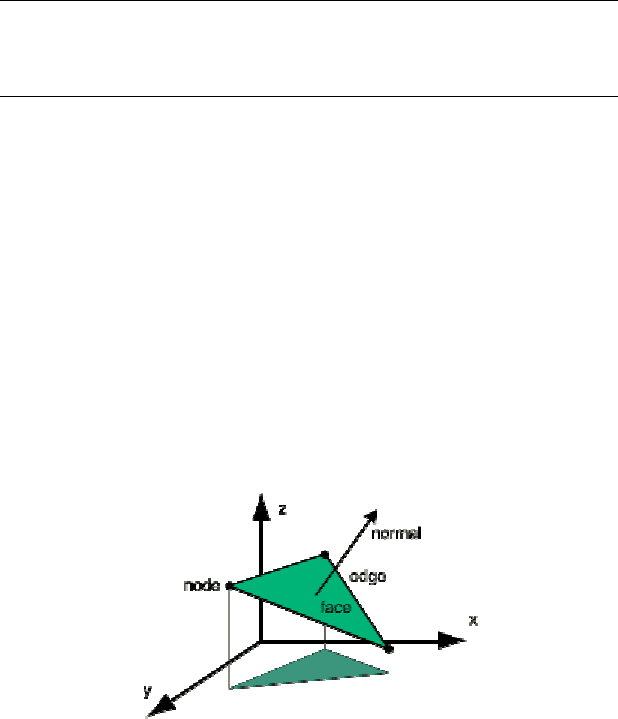
Рис. 2.5.1 – Геометрия модели TIN [29]
Геометрия модели TIN образуется гранями, узлами и ребрами в
трехмерном пространстве.
Грань (Face) – поверхность треугольника в трехмерном
пространстве.
Узел (Node) – вершина треугольника с координатами
X,Y,Z.
Ребро (Edge) – сторона треугольника в трехмерном
пространстве.

124
Каждая грань TIN является частью поверхности в 3D-пространстве.
Модель TIN является альтернативой растровым DEM и
используются во многих геоинформационных системах, системах
автоматизированного картографирования. Модели TIN разработаны в
1970-х годах как простой способ построения поверхностей по
нерегулярно расположенным точкам.
Рис. 2.5.2 – Пример отображения фрагмента поверхности стоимости
земли моделью TIN
2.5.2 Свойства модели TIN
Модель TIN обладает следующими свойствами:
Модель TIN позволяет получить точное представление о
локальной части поверхности, используя переменную
плотность узлов со значением Z и линии перегиба
поверхности;
Модель TIN является основой 3D-визуализации поверхности;
Модель TIN позволяет выполнить сложный анализ
поверхности (вычисление высот, уклонов, экспозиций
склонов, получение изолиний поверхности, расчеты объемов,
вертикальные профили по трассе линии, анализ видимости).
125
2.5.3 Триангуляция Делоне
Исходными данными для построения TIN является набор точек с
координатами X,Y,Z. Задача заключается в том, чтобы по этому
набору точек создать сеть смежных непересекающихся треугольников.
Задача построения триангуляции по набору точек является одной из
базовых в вычислительной геометрии. К ней сводятся многие другие
задачи, она широко используется в машинной графике и
геоинформационных системах для моделирования поверхностей и
решения пространственных задач.
Задача построения триангуляции по исходному набору точек
является неоднозначной, поэтому возникает вопрос, какая из
различных триангуляций лучше? Можно, например, оптимальным
решением считать такое, при котором сумма длин всех рёбер будет
минимальной среди всех возможных триангуляций, построенных на
тех же исходных точках. Решение задачи при таком условии имеет
высокую трудоёмкость [34].
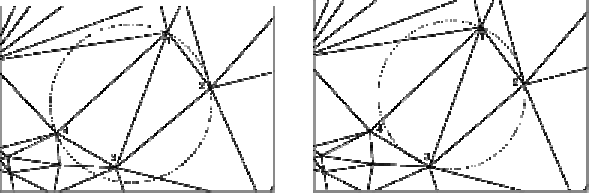
а) б)
Рис.2.5.3 – Формирование треугольника в триангуляции Делоне: а)
круг, построенный по точкам 1,2,4, включает точку 3; b) круг,
построенный по точкам 1,2,3, не включает точку 4.
Наибольшее распространение в ГИС получила триангуляция
Делоне (Delaunay), которая названа по имени ее автора советского
математика Бориса Николаевича Делоне (1890-1980). По определению
Делоне три точки формируют треугольник в триангуляции тогда и
только тогда, когда в окружности, описанной вокруг этого
треугольника нет других точек разбиения. Каждый ограничивающий
треугольник круг не содержит точек из набора внутри его (рис.2.5.3,б).
Один из алгоритмов построения триангуляции Делоне основан на
генерировании полигонов Тиссена (Thiessen) или Вороного. Для этого
поверхность разбивается на области, в которых каждая точка
126
расположена ближе всего к некоторому узлу сети – генерирующей
точке. Полученные границы называют полигонами Тиссена или
полигонами Вороного. Две точки соединяются линией в триангуляции
Делоне, если их полигоны Тиссена имеют общую границу. Этот метод
позволяет получить требуемые треугольники. Полигоны Тиссена
используются также при анализе близости.
Рис. 2.5.4 - Полигоны Тиссена
2.5.4 Топология в TIN
Модель TIN – это топологическая структура данных: ребра
соединяются в узлах; каждый треугольник смежный с соседними
треугольниками.
Топологические отношения создаются путем создания в базе
данных для каждого узла указания на смежные узлы. Пространство
вокруг территории представляется фиктивным узлом.
Рис. 2.5.5 - Модель TIN

127
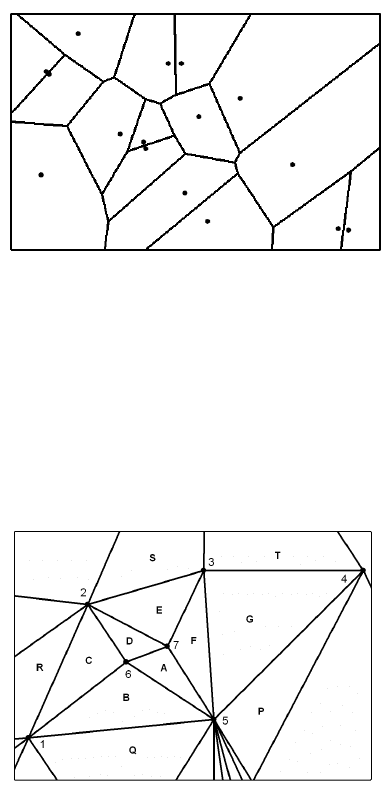
Модель TIN (рис. 2.5.5) в цифровом виде описывается связанными
файлами - файлом вершин (табл.2.5.1), файлом указателей и файлом
треугольников (табл.2.5.2). Для каждой точки разбиения сохраняется
ее уникальный номер, координаты и список точек, с которыми она
соединена прямыми (по часовой стрелке).
Табл.2.5.1 – Список вершин
Вершина X Y Z
1 X
1
Y
2
Z
3
2 X
2
Y
2
Z
2
3 X
3
Y
3
Z
3
4 X
4
Y
4
Z
4
5 X
5
Y
5
Z
5
6 X
6
Y
6
Z
6
7 X
7
Y
7
Z
7
Табл.2.5.2 – Список треугольников
Треугольник Вершины Смежные
треугольники
A 5 6 7 B D F
B 1 5 6 A C Q
C 1 2 6 B D R
D 2 6 7 A C E
E 2 3 7 D F S
F 3 5 7 A E G
G 3 4 5 F T P
128
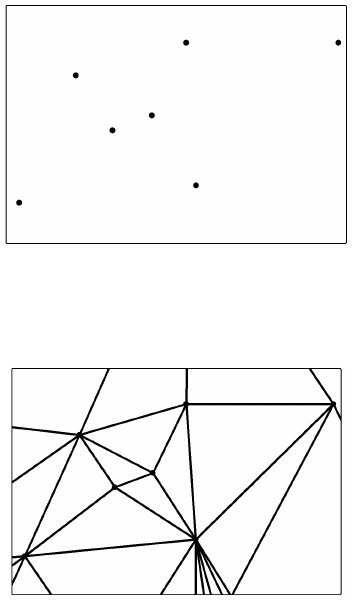
2.5.5 Этапы создания модели TIN
Модель TIN создается в следующей последовательности.
Этап 1. Задание множества точек i по координатам X
i
, Y
i
, Z
i
.
Рис. 2.5.6 - Множество точек
Этап 2. Построение триангуляция Делоне
Рис. 2.5.7 – Триангуляция Делоне
Этап 3. Ввод линий перегиба поверхности (Breakline) и модификация
TIN с учетом линий перегиба. Линии перегиба рельефа определяют
резкие изменения поверхности, такие как линия верха, низа откоса,
гребни, тальвеги и др.
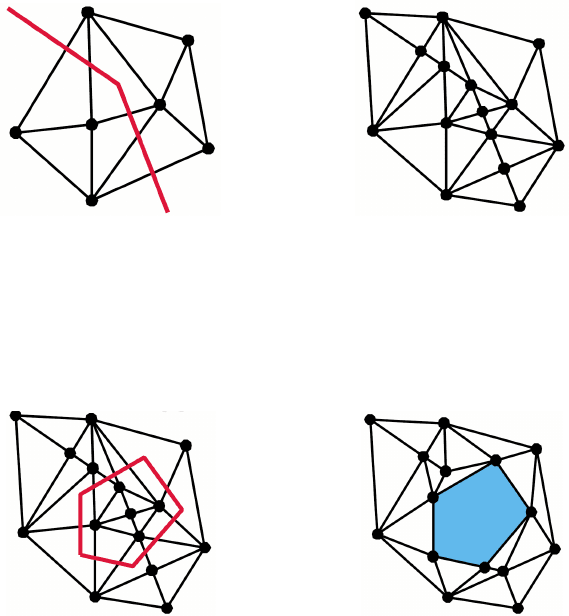
129
Рис. 2.5.8 – Линии перегиба поверхности [29]
Этап 4. Ввод областей исключения (Exclusion areas) с постоянным
значением Z и модификация TIN с учетом полигональных объектов,
например водной поверхности.
Рис. 2.5.9 - Области исключения [29]
Этап 5. Решение задач по модели TIN поверхности.
2.5.6 У равнение нормали к грани треугольника
В TIN-модели пространственное положение треугольника
характеризует нормаль к его грани.
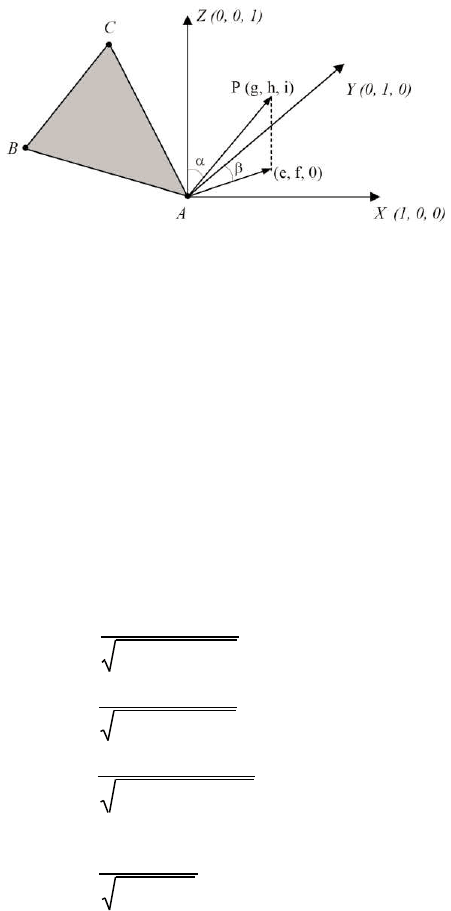
130
Рис.2.5.10 – Нормаль Р к грани треугольника
Треугольник задается тремя точками (x
a
,y
a
), (x
b
,y
b
), (x
c
,y
c
).
Нормаль P к плоскости треугольника определяется нормальным
вектором P = {p
a
, p
b
, p
c
}, который получается врезультате векторного
произведения векторов АВ и АС двух его сторон. Для нормального
вектора Р каждого треугольника вычисляются:
1) прямоугольные декартовы координаты:
[
]
[ ]
[ ]
)(*)()(*)(
)(*)()(*)(
)(*)()(*)(
acabacabc
acabacabb
acabacaba
xxyyyyxxp
zzxxxxzzp
yyzzzzyyp
−−−−−=
−−−−−=
−−−−−=
(2.5.1)
2) направляющие косинусы:
222
cba
a
ppp
p
g
++
=
(2.5.2)
222
cba
b
ppp
p
h
++
=
(2.5.3)
222
cba
c
ppp
p
i
++
=
( 2.5.4)
3) проекции к горизонтальной плоскости:
22
ba
a
pp
p
e
+
=
(2.5.5)
