Shen S., Tuszynski J.A. Theory and Mathematical Methods for Bioformatics

Подождите немного. Документ загружается.

324 11 Alignment of Primary and Three-Dimensional Structures of Proteins

Exercise 56. For the torsion angle sequences Ψ

, implement the pairwise

alignment by the dynamic programming algorithm with the measure func-

tion given in formula (11.7), to ﬁnd the pairwise minimum penalty alignment

and the homology matrix of the pairwise alignment of these sequences.

Exercise 57. Visualize the 3D structure of each protein in Exercise 54 using,

for example, the Rasmol software package, and compare the relationship be-

tween the homologies and the conﬁgurations of diﬀerent proteins. Visualize

the 3D structures of the 15 models of protein PDB1BF9 in the same way, and

compare the homology with Table 11.4.

Depth Analysis of Protein Spatial Structure

12.1 Depth Analysis of Amino Acids in Proteins

The depth of amino acids in a protein has been deﬁned in many ways. For

example, in biology, the amino acids, which come in contact with water

molecules, form the surface of protein (zero depth) [54], so we may use this to

determine the hydrophobic property of amino acids. Although these biologi-

cal deﬁnitions have a clear physical sense, they lack a uniform computational

methodology. For example, the concept of the hydrophobic factor of amino

acids has been deﬁned in many ways.

In mathematics, there are a series of deﬁnitions and calculational methods

for the depth in a spatial particle system. How to apply these results and

methods to the research of protein spatial structure will be discussed in this

section.

12.1.1 Introduction to the Concept of Depth

We begin by introducing the basic mathematical concepts, deﬁnitions and

generalization of depth in spatial particle systems.

Two Kinds of Deﬁnitions

There are two kinds of deﬁnitions of depth in mathematics, one is the gener-

alization of the Tukey depth [103] in statistics, and the other is the accessible

radius function theory in spatial particle systems:

1. The deﬁnition of Tukey depth comes from statistical theory. The median is

a typical concept of “the deepest point” which is very important to statis-

tics. The generalization of the median is the depth of one-dimensional

data and high-dimensional data, and the deﬁnition of two-dimensional

data is shown in the ﬁgure below. For one-dimensional data, they are well

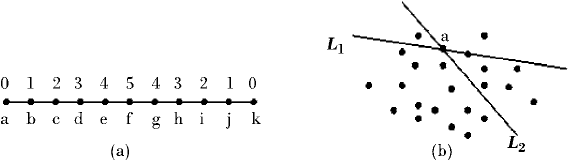
326 12 Depth Analysis of Protein Spatial Structure

Fig. 12.1a,b. Depth of one-dimensional and two-dimensional data points

ordered, which implies that their depth can be quickly determined. How-

ever, for high-dimensional cases, the data are only semiordered. There-

fore, we need methods to describe the depth. In modern statistical theory,

there are a series of studies on both the deﬁnition and calculation of

depth [58,72, 80, 103,114–116]. Since the concept of depth determines the

relative position of the points in space, we can use it to analyze protein

spatial structure.

Figure 12.1a shows the depth of one-dimensional data; where a, b, ··· ,k,

are the points on a straight line, and the corresponding numbers are their

depth. Figure 12.1b represents two-dimensional data, where we can see

both interior points and exterior points, whose depth cannot be deter-

mined directly, but requires further statistical analysis.

In Fig. 12.1b, solid points represent all the points in a spatial particle

system. L

and L

are straight lines passing through the point a,and

these lines separate the set A into two parts. While rotating the line

around point a, the corresponding fewest number of points that lie on one

side of the line is the depth of point a in set A.

2. The accessible radius function theory in spatial particle systems is a bio-

logical concept of depth represented through the language of mathematics.

It shows the largest possible radius within which each particle in A is in

contact with the exterior. We will discuss this theory in detail below.

Protein Depth in Spatial Particle Systems

If we consider all proteins (or select partsofatoms)asaspatialparticle

system, then the spatial location of these atoms in the particle system can be

used to analyze depth. In this book, we discuss the following issues:

1. On the basis of calculating depth, we can build a depth database of pro-

teins. It means that we can calculate the depth of the amino acids (or

atoms) of all proteins (or peptides) in the PDB database, and build

a depth database of proteins.

2. On the basis of the above depth database, we can do statistical depth

analysis for diﬀerent amino acids, such as depth tendency factor analysis,

hierarchical analysis, and depth analysis of the peptide chain.

12.1 Depth Analysis of Amino Acids in Proteins 327

3. On the basis of depth analysis, we can do further analysis for special shapes

of proteins, such as calculating the accessible radius function, calculating

the interior structure of protein, and so on. We will discuss these issues in

detail in the following text.

Mathematical Tools for Finding the Depth in Spatial Particle

Systems

To analyze the depth of a spatial particle system, we use a variety of mathe-

matical tools, such as the depth function algorithm, the geometric theory of

convex polygons and hypergraph theory. We apply large-scale knowledge of

analytic space geometry in the calculations.

12.1.2 Deﬁnition and Calculation of Depth

Before analyzing protein structure, we introduce the general theory of depth.

In order to analyze protein structure, we give further discussion about both

the calculation and properties of depth.

Deﬁnition of the Depth of a Discrete Set in 3D Space

Let

A =(a

, ··· ,a

) , (12.1)

be a set of points in 3D space R

, and denote the three-dimensional coordinate

of each point a

by r

=(x

). Let π be a plane that contains the

point a. Then, the plane cuts the set A into two parts, respectively denoted

by A

(π, a)andA

(π, a), which are located on two diﬀerent sides of π.Let

(π, a) be the number of elements contained in the set A

(π, a), τ =1, 2.

We always assume that n

(π, a) ≤ n

(π, a).

Deﬁnition 42. For a ﬁxed point a and set A, we have the following deﬁni-

tions:

1. The depth of point a in set A is deﬁned as

(a)=min{n

(π, a): π ∈

Π(a)} , (12.2)

in which

Π(a) is a plane that contains point a.

2. Let π

be a plane that contains point a such that n

(π

,a)=s

(a),then

we call π

a depth cut plane that contains point a.

3. If π

is a depth cut plane that contains point a, we call the side which

contains A

(π

,a) the outside of the depth cut plane. We call the other

side the inside of the depth cut plane.

328 12 Depth Analysis of Protein Spatial Structure

Fast Calculation of Depth

In Deﬁnition 42, since

Π(a) is an inﬁnite set, there is actually no way to

calculate s

(a) in (12.2). Therefore, we ﬁrst give some easily applied formulas

for calculating depth.

Let π(a; i, j) be a plane that contains three points (a, a

), where

∈ A. Then, the plane π(a; i, j) cuts the set A

[π(a; i, j)], τ =1, 2

into two parts, respectively denoted by A1 and A2, located on two diﬀer-

ent sides of plane π(a; i, j). Let n

[π(a; i, j)], τ =1, 2bethenumberof

elements contained in set A

[π(a; i, j)], τ =1, 2, and always assume that

[π(a; i, j)] ≤ n

[π(a; i, j)].

For a given point a,anda

∈ A that may change, let s



(a)denotethe

minimum of n

[π(a; i, j)]. Then the depth s

(a)ofthepointa in set A is just



(a).

Theorem 40. The formula to compute the depth of point a in set A is given

as follows:

(a)=min{n

[π(a; i, j)] : a

= a

∈ A, and a, a

are noncollinear} .

(12.3)

We will prove this theorem in Sect. 12.1.3. Thus, calculating the depth of

point a can be simpliﬁed into calculating n

[π(a; i, j)], where a

∈ A.There-

fore, the computational complexity is no more than O(n

), and we obtain the

fast calculation of the depth of point a in set A.

The depth cut plane of point a can be restricted to a triangular area which

is constructed by point a and two other points a

in set A.Letπ(a, a

)

be a depth cut plane that contains point a. We then call triangle δ(a, a

)

the depth cut triangle of point a. Deﬁnitions of both the outside and inside

of the depth cut triangle are determined by the corresponding outside and

inside of the depth cut plane.

We can generalize the deﬁnition and fast calculation of depth to two-

dimensional or higher dimensional point sets in the same way, so we will not

repeat these here. Set A in Fig. 12.1 represents two-dimensional data. There

might be many lines like L

and L

passing through point a,andtheyallcut

the set A into two parts. The corresponding number of points are n

)=2,

) = 19, n

)=7,n

) = 15, where L

is a cutting line. So the

depth of a is s

(a)=2.

Remark 19. For the formula in Theorem 40, a may not be a point in set A.

This means that for any point a ∈ R

, formula (12.2) holds.

Several Properties of Depth

According to the deﬁnition of depth and the formula in Theorem 40, we im-

mediately obtain the following properties:

12.1 Depth Analysis of Amino Acids in Proteins 329

Fig. 12.2. The convex hull, groove, and cavity of a two-dimensional particle. The

thick line is the convex closure Ω(A)ofsetA (their depths are zero), and the thin

lines represent the interior groove and cavity of the convex closure Ω(A)

1. If A is a ﬁxed ﬁnite set and a is an arbitrary point in space R

,thens

(a)

is uniquely determined, and 0 ≤ s

(a) ≤ int(n/2) is true, where n = ||A||,

and int(n/2) is the integral part of n/2.

2. If all points in A are coplanar, then the depth of each point in A is zero.

3. If Π

is a depth cut plane of a

,anda ∈ A is in the plane Π

,then

(a) ≤ s

)holds.Ifa ∈ A is in outside of Π

(namely, it is in

(Π

)), then s

(a) <s

)holds.

4. Let Ω(A) be a convex closure of the setA;thens

(a) = 0 if and only if

is on the boundary plane of Ω(A).

These properties can be easily deduced from Figs. 12.1 and 12.2.

Theorem 41. Let s

be the maximum of s

(a), a ∈ A.Then,s

is called

the deepest depth of set A.DenotebyS

the set of points in R

whose depth

is s

.Then,S

is deﬁnitely a convex set, and this convex set does not contain

any four points which are not coplanar in set A.

We will prove this theorem in Sect. 12.1.4.

12.1.3 Proof of Theorem 40

Part One: Preliminary Nature

To prove Theorem 40, we must discuss the property of a plane turning around

a straight line. We use the following symbols:

1. π is a plane in 3D space, whose normal vector is denoted by b,withb and

plane π being vertical. We denote by  a directed line which lies in plane

π; the direction of  is arbitrarily selected, with its direction denoted by

the vector c.

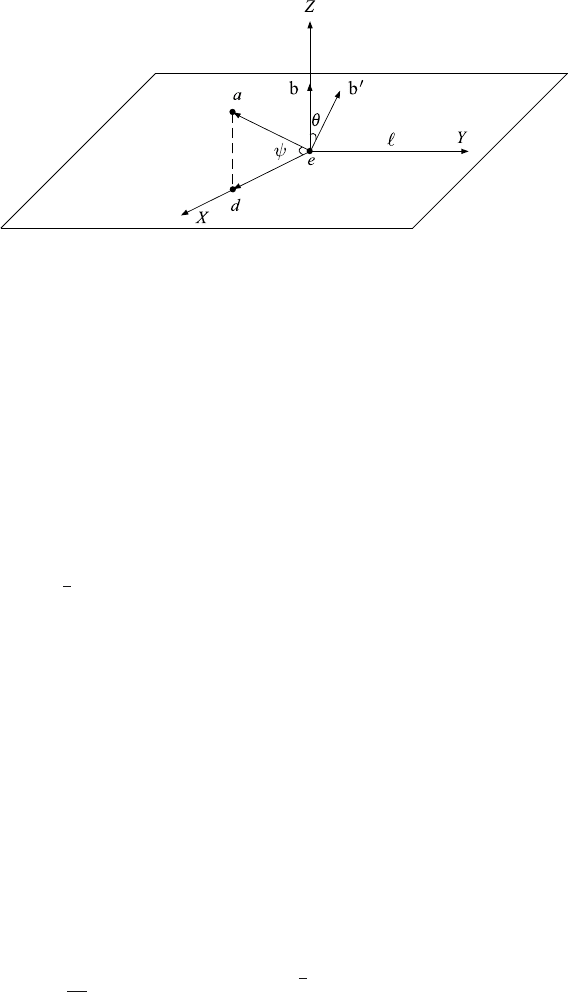
330 12 Depth Analysis of Protein Spatial Structure

Fig. 12.3. Y-axis of the coordinate system is determined by the right-hand screw

rule

2. Let a be a point which is not in plane π. We project a on to both plane

π and line , and obtain two projective points denoted by d, e.Denote

b =

−→

da, d =

−→

ed.

3. Let a, b be the inner product of a and b; here the sign of a, b may be

negative or positive. Deﬁne sgn(a, b), where

sgn (u)=



1 , if u ≥ 0 ,

−1 , if u<0 ,

is the sign function of u.

4. Let ψ =



aed be the angle between a and d,then− π/2 <ψ≤ π/2. We

provide the following rules: if e = d, which means that ae is perpendicular

to plane π,thenweletψ = ±π/2. if sgn (a, b)=+1,ψ>0; otherwise

we let ψ<0.

5. When plane Π is turning around line ,wecreateanewplaneΠ



,whose

normal vector is denoted by b



. The rotating dihedral angle, namely the

angle θ between b



and b,hasrange|θ|≤π/2. Its sign (positive or nega-

tive) is determined by the right-hand rule. We have the following proper-

ties.

Lemma 5. If |θ| < |ψ|,then

sgn (b, a)=sgn(b



, a) . (12.4)

Proof. We begin to determine a rectangular coordinate system E.Lete be

the origin, and the X-axis and Z-axis are determined by vector

−→

ed and b.The

Y-axis is determined by the right-hand screw rule (Fig. 12.3).

Point a is in the plane XZ, ψ =



aed; without loss of generality, let

b =(0, 0, 1), |

ea| =1then,a =(cosψ, 0, sin ψ)andb, a =sinψ.

When plane Π is turning around line  with angle θ,thenb



=(sinθ, 0,

cos θ).

b



, a =sinθ cos ψ +sinψ cos θ =sin(ψ + θ)

12.1 Depth Analysis of Amino Acids in Proteins 331

Since |θ| < |ψ| if 0 <ψ≤

, −ψ<θ<ψand 0 <ψ+ θ<2ψ ≤ π,

we get sgn (sin ψ) = sgn [sin(ψ + θ)]. If −

≤ ψ<0, ψ<θ<−ψ and

2ψ<ψ+ θ<0, we also ﬁnd that sgn (sin ψ) = sgn [sin(ψ + θ)] holds. Thus,

the theorem is proved.

Properties of a Plane Turning Around a Point

Lemma 5 suggests that the inner product changes if a plane is turning around

a line. To discuss this in detail, we introduce the following notations.

Let b, b



,andr be three arbitrary vectors whose inner products are b, r,

b



, r.Letθ, ψ be the angle between b and b



, r, respectively, in which 0 ≤ θ,

ψ ≤ π.

Lemma 6. If θ and ψ satisfy either of the following conditions, then

sgn (b, r)=sgn(b



, r) . (12.5)

Condition 1 If 0 ≤ ψ ≤ π/2,and 0 ≤ θ ≤ π/2 −ψ ≤ π/2.

Condition 2 If π/2 ≤ ψ ≤ π,and 0 ≤ θ ≤ ψ − π/2 ≤ π/2.

Proof. For the sake of simplicity, in a rectangular coordinate system, we take

b =(0, 0, 1) , r =(0, sin ψ, cos ψ) , b



=(cosφ sin θ, sin φ sin θ, cos θ) ,

in which, φ is from (0, 2π). Then

sgn (b, r)=sgn[cosψ]=



+1 , if 0 ≤ ψ ≤ π/2 ,

−1 , if π/2 <ψ≤ π

We calculate the value of sgn (b



, r). Here

b



, r =sinψ sin φ sin θ +cosψ cos θ. (12.6)

Toﬁnishtheproofofthelemma,wediscussthefollowingtwosteps:

1. If 0 ≤ ψ ≤ π/2, 0 ≤ θ ≤ π/2 − ψ ≤ π/2 (Fig. 12.4a), then cos ψ ≥ 0.

Therefore, we need only prove b



, r≥0. Following from (12.6), we have

b



, r≥cos ψ cos θ − sin ψ sin θ =cos(ψ + θ) ≥ 0

and since sin ψ, sin θ ≥ 0, sin φ ≥−1, 0 ≤ ψ + θ ≤ π/2. This implies that

b



, r≥0 holds. Thus the lemma is true under condition 1.

2. If π/2 ≤ ψ ≤ π, 0 ≤ θ ≤ ψ − π/2 ≤ π/2 (Fig. 12.4b), then cos ψ ≤ 0, so

we need only prove b



, r≤0. Following from (12.6), we have

b



, r≤cos ψ cos θ +sinψ sin θ =cos(ψ − θ) ≤ 0 .

Since sin ψ, sin θ ≥ 0, sin φ ≤ 1,π/2 ≤ ψ − θ ≤ π, we ﬁnd that b



, r≤0

holds. Additionally, cos ψ = 0 implies that cos(ψ − θ)=0.Thusthe

lemma is true under condition two, and the lemma is shown to be true in

its entirety.

332 12 Depth Analysis of Protein Spatial Structure

Fig. 12.4a,b. Proof of Lemma 6

Part Two: Proof of Theorem 40

Let s



(a) be the depth deﬁned by (12.3); obviously, we have that s



(a) ≥

(a). Thus, we need only prove that s



(a) ≤ s

(a)holds.

According to the deﬁnition of s

(a), we realize that, for an arbitrary

point a, there must be a plane π

∈

Π(a), such that n

(π

,a)=s

(a).

Three cases may occur on plane π

1. Case 1. There are two points a

= a

∈ A such that a, a

are not

collinear.

In this case, Π

∈

(a) implies n

(π

,a)=s

(a) ≥ s



(a); thus we have

that s

(a)=s



(a)holds.

2. Case 2. There is one point in plane π

such that a

= a ∈ π

, while the

remaining points in A are neither in plane π

, nor on line 

,where

is a line determined by points a and a

Line 

must be in plane Π

, so we denote the set of points which are

in A, while not in plane π

,byA



If a

∈ A



,lete

and d

denote the projection of a

onto the line 

and

plane π

, respectively, and let the sign of ψ



be determined

by the sign of a

, b.Moreover,let

=min{|ψ

|: a

∈ A



}

and a

∈ A



such that |ψ

| = ψ

. We then have the following conclusions:

(a) ψ

> 0, otherwise a

∈ Π

, which contradicts the deﬁnition of A



(b) Point a

must be in A

. Otherwise, we assume that point a

in A

,whenΠ

is rotating around line 

with angle ψ

,andwe

create a new plane Π



which is also through points a, a

and point a

Several cases may arise according to the points in A



i. ψ

= ψ

, as shown in Fig. 12.5a, e

and e

have the same

direction, so point a

falls in plane Π



12.1 Depth Analysis of Amino Acids in Proteins 333

Fig. 12.5a,b. ProofofTheorem40

ii. ψ

= ψ

, as shown in Fig. 12.5b, the angle formed by e

and

is π − 2ψ

Let the direction of

and e

be the direction of the z-axis

and x-axis, and let the origin be e

. We then form a right carte-

sian coordinate system, and without loss of generality, we may set

b =(0, 0, 1), |

| = 1. This implies a

=(cosψ

, 0, sin ψ

) b



(sin ψ

, 0, cos ψ

), in which 0 <ψ

≤

.Wethenhave

ba

 =sinψ

b



 =2sinψ

cos ψ

Thus,wehavethatsgnba

 =sgnb



 holds.

iii. In the case where ψ

= −ψ

, the situation is similar to that in

case 2; two cases may occur and we have the same discussion.

iv. |ψ

| >ψ

. In this case, we may follow from Lemma 5 to get (12.4).

Therefore, we have

(π



,a) <n

(π

,a)=s

(a) .

This contradicts the deﬁnition of s

(a). Thus, point a

must be-

long to A

v. If a

belongs to A

, then with the same arguments used in

case 2, rotating Π

around line 

with angle ψ

, we get a new

plane Π



.Herepointsa, a

are still in plane Π



, and the sphere

is through point a

. This is similar to case 2, the point a

in A



may either fall in plane Π



, or keep (12.5) stable, thus, we get



(a) ≤ n

(Π



,a) ≤ n

(Π

,a)=s

(a) .

As a result, we ﬁnd that s



(a)=s

(a)holds.

3. Case 3. The remaining points in A are not in Π

.Wedenotea

= aa

and denote the angle between a

and b

by ψ

,where0≤ ψ

≤ π,and

is the normal vector of π

. We now denote





, if 0 ≤ ψ

<π/2 ,

π − ψ

, if π/2 ≤ ψ

≤ π,

(12.7)