Шехтман В.Е. Базы данных, SQL и все такое. Курс лекций
Подождите немного. Документ загружается.


39
2. Аномалия добавления. В отношение нельзя включить поставщика, если он не
осуществил ни одной поставки. Однако зачастую требуется учесть поставщика,
данные о котором потенциально могут понадобиться.
3. Аномалия удаления. При удалении факта поступления товара от поставщика
может потеряться и информация об этом поставщике, хотя она может
пригодиться в дальнейшем.
Нормализация – разбиение таблицы на две или более, обладающие лучшими
свойствами при добавлении, изменении и удалении данных.
Основные вопросы, на которые следует ответить при нормализации:
1. Образует ли данная совокупность проекций отношения полную декомпозицию?
2. Разбивать ли отношения на проекции и если разбивать, то как?
Неформально цель нормализации можно описать так: один факт из предметной
области должен храниться в одном месте (в одной записи одного отношения базы
данных).
5.5 Пятая нормальная форма (5НФ)
Можно отметить, исходя из анализа примеров с отношением P=(КОДТОВАРА,
ПОСТАВЩИК, ТЕЛ), что невозможность устранения дублирования и решения
проблемы присоединенных записей связана с присутствием в проекциях отношения
общего возможного ключа исходного отношения (это утверждение можно доказать
строго). Напомним, что возможный ключ отношения – это минимальный набор полей,
значения которых однозначно идентифицируют кортеж отношения. Исходя из этого
наблюдения, введем определение:
Отношение находится в 5НФ, если не существует ни одной полной
декомпозиции, в которую входили бы проекции, не имеющие общего возможного ключа.
Иными словами, отношение находится в 5НФ, если в любой его полной
декомпозиции все проекции содержат возможный ключ исходного отношения.
Считаем, что если отношение не обладает ни одной полной декомпозицией, то оно в
5НФ. Исходя из примеров, можем сказать, что отношение в 5НФ не имеет смысла
заменять какой-либо полной декомпозицией, т. к. это не дает преимуществ в смысле
устранения дублирования и решения проблемы висячих (присоединенных) записей.
Но если отношение не в 5НФ, то можно заменить его полной декомпозицией, в
которой проекции не содержат общего возможного ключа исходного отношения. Если
полученные таким образом проекции в свою очередь не в 5НФ, то каждую из них
можно заменить полной декомпозицией, сформированной из проекций в 5НФ. Этот
процесс и составляет суть нормализации.
Пример: пусть имеется отношение
НомерДома
Тип
Этажей
Лифт
1
Полнометражный
7
Есть
2
Улучш. Планировки
12
Есть
3
Полнометражный
5
Нет
4
Хрущевка
5
Нет
Подумайте, какая из декомпозиций подходит для нормализации этого отношения
(позволяет устранить дублирование и хранить присоединенные записи):
1. НомерДома, Тип, Этажность;
НомерДома, Лифт .
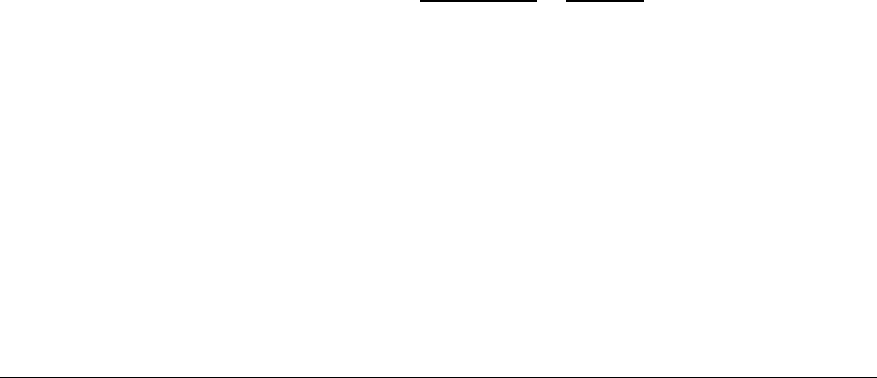
40
2. НомерДома, Тип;
НомерДома, Этажность;
НомерДома, Лифт.
3. НомерДома, Тип, Этажность;
Тип, Лифт.
4. НомерДома, Тип, Этажность;
Тип, Этажность, Лифт.
5.6 Функциональная зависимость
До сих пор мы не использовали явного критерия, который бы позволял
установить, образует ли данный набор проекций полную декомпозицию. Чтобы его
сформулировать, введем понятие функциональной зависимости (ФЗ).
Пусть X и Y – наборы полей отношения R. Y функционально зависит от X тогда
и только тогда, когда каждому значению X сопоставлено не более одного значения Y.
(обозначают X→Y).
При наличии X→Y любые две записи, содержащие одинаковые значения X,
должны включать и совпадающие значения Y. Это ограничение распространяется не
только на уже имеющиеся записи, но и на те, которые могут быть добавлены в
рассматриваемое отношение. Пусть R(F1, F2):
F1 F2
A h
B i
C j
B k
Видно, что F2 не зависит функционально от F1, т.к. значению B соответствуют
два разных значения (i, k). Можно предположить, что F2→F1. Однако положительно
утверждать это можно было бы только при условии, что в отношение нельзя ввести
запись, нарушающую однозначное соответствие поля F2 полю F1 (например, (C, k)).
Если X – составное поле, то Y находится в полной функциональной зависимости
от X тогда и только тогда, когда:
1. Y функционально зависит от X
2. Y не зависит функционально от любого подмножества полей, входящих в X, не
совпадающего с X.
Пример:
Вспомним отношение S = (МАГАЗИН, ТОВАР, НДС). В нем НДС
функционально зависит от пары МАГАЗИН и ТОВАР (действительно, любой такой
паре значений соответствует одно и то же значение НДС). Но по смыслу этой
величины, НДС зависит только от поля ТОВАР. Следовательно, НДС не обладает
полной функциональной зависимостью от пары МАГАЗИН, ТОВАР (но обладает
полной функциональной зависимостью от поля ТОВАР).
В терминах функциональной зависимости можно дать более точное определение
ключа отношения:
Атрибуты X отношения R составляют ключ этого отношения, если все прочие
атрибуты R, не входящие в X, функционально полно зависят от X.

41
5.7 Связь между функциональной зависимостью и полной
декомпозицией отношения
Соединение проекций отношения R по условию совпадения общих атрибутов
всегда является надмножеством исходного отношения. Иногда это истинное
надмножество, т. е. оно включает кортежи, которые отсутствовали в исходном
отношении (см. раздел 5.1). Однако, как мы имели возможность убедиться, иногда
удается подобрать полную декомпозицию, т. е. обеспечить возможность получения
точного исходного отношения путем соединения проекций. Критерий, гарантирующий
такую возможность, устанавливается теоремой Хита.
Пусть отношение R = (A, B, C) (A, B, C – возможно составные поля).
Теорема Хита (Heath): если A→B, то R = proj
A,B
R join proj
A,C
R.
Доказательство проведем от противного (чтобы доказать, что из P следует Q,
достаточно доказать, что из отрицания Q следует отрицание P). А именно, докажем, что
из факта R <> proj
A,B
R join proj
A,C
R следует, что B не зависит функционально от A.
Для краткости здесь и далее в доказательствах примем такую форму записи
операции проекции: proj
A,C
R = R[A,C].
Доказательство:
Предположим, что (a, b, c) R[A, B] join R[A, C], но (a, b, c) R. Тогда (a, b)
R[A, B], (a, с) R[A, С]. Следовательно, имеются (a, b, c‘) R и (a, b‘, c) R такие, что
c <> c‘, b <> b‘. Следовательно, отсутствует функциональная зависимость A → B.
Итак, доказано, что при наличии функциональной зависимости B от A проекции
R[A, B] и R[A, C] образуют полную декомпозицию R.
Еще один способ доказательства:
Пусть J→K и R1 = R[H,J] join R[J,K]. Возьмем произвольную запись из R: (h, j,
k). Очевидно, (h, j) R[H,J], (j,k) R[J,K]. Исходя из определения R1 и свойств
операции условного соединения, можно заключить, что (h, j, k) R1. Следовательно,
каждая запись R принадлежит R1.
Возьмем произвольную запись из R1: (h‘, j‘, k). Известно, что R1[H, J] = R[H, J]
(по определению R1). Следовательно, (h‘, j‘, k) R. Кроме того, R1[J, K] = R[J, K] (по
определению R1). Следовательно, (h, j‘, k‘) R. Т. к. по условию теоремы, J→K, то из
наличия записей (h‘, j‘, k) и (h, j‘, k‘) следует, что k=k‘. Следовательно, каждая запись
R1 принадлежит R. Следовательно, R1=R.
Рассмотрим иерархию степеней ―совершенства‖ свойств отношений. В этой
иерархии 5НФ является ―венцом совершенства‖ а остальные формы – приближением к
нему.
5.8 Первая нормальная форма (1НФ)
Отношение находится в 1НФ тогда и только тогда, когда ни одна из его
записей не содержит в поле более одного значения и ни одно из ключевых полей не
пусто.
Эта форма обладает наиболее общими чертами среди прочих нормальных форм
отношений. Любое отношение находится в 1НФ (согласно определению отношения,
см. выше). 1НФ не обеспечивает свободу от аномалий, связанных с несовершенной

42
структурой данных (см. п.5.4.) По существу, приведенное определение избыточно, т. к.
1НФ – это любое ―настоящее‖ отношение, т. е. подмножество декартова произведения
доменов (см. раздел 2 Введение в реляционную модель данных).
5.9 Вторая нормальная форма (2НФ)
Будем называть непервичным атрибутом всякий атрибут отношения, не
являющийся членом какого-либо ключа отношения.
Отношение находится во второй нормальной форме, если оно находится в
первой нормальной форме и не содержит неполных функциональных зависимостей
непервичных атрибутов от первичного ключа.
Пример:
Вернемся к отношению S = (МАГАЗИН, ТОВАР, НДС). Первичный ключ здесь
– пара (МАГАЗИН, ТОВАР), но НДС зависит от поля ТОВАР, следовательно не
находится в полной функциональной зависимости от первичного ключа. Значит, S не
находится в 2НФ.
Напротив, отношение P = (КОДТОВАРА, ПОСТАВЩИК, ТЕЛ) находится в
2НФ, т. к. поля ПОСТАВЩИК и ТЕЛ функционально полно зависят от первичного
ключа КОДТОВАРА. 2НФ все еще не обеспечивает свободу от аномалий (см. раздел
5.4).
Покажем, что отношение, не находящееся в 2НФ, не может быть и в 5НФ. Пусть
R = (J, K, H). J – первичный ключ, K – функционально полно зависит от J, H – не
зависит от J. По теореме Хита, из наличия J→K следует R = R[H, J] join R[J, K].
Проекции не имеют общего возможного ключа. Следовательно, R не находится в 5НФ
и его можно ―усовершенствовать‖ декомпозицией.
5.10 Третья нормальная форма (3НФ)
Отношение находится в третьей нормальной форме, если и только если оно
находится во второй нормальной форме и ни одно из его неключевых полей не зависит
функционально от любого другого неключевого поля (т.е. отсутствуют
транзитивные функциональные зависимости).
Можно сказать и иначе: Отношение находится в третьей нормальной форме, если в
случае существования функциональной зависимости X→Y, X является ключом или Y
является членом какого-то другого ключа (т. е. Y не является непервичным атрибутом
(см. определение 2НФ)).
Пример:
Отношение P = (КОДТОВАРА, ПОСТАВЩИК, ТЕЛ) не находится в 3НФ, т. к.
поле ТЕЛ функционально зависит от поля ПОСТАВЩИК, хотя поле поставщик не
является ключом (первичным ключом здесь является KOДТОВАРА). Поэтому это
отношение можно нормализовать: proj
КОДТОВАРА, ПОСТАВЩИК
R и proj
ПОСТАВЩИК, ТЕЛ
R. Эти
проекции уже находятся в 3НФ т. к. КОДТОВАРА → ПОСТАВЩИК и ПОСТАВЩИК
→ ТЕЛ и отсутствуют какие либо иные функциональные зависимости.
Пример:

43
Пусть имеется отношение ПРОИЗВОДСТВО (ДЕТАЛЬ, ЦЕХ, ЗАВОД), кортеж
которого хранит сведения о том, какие детали производятся сейчас в соответсвующих
цехах каждого из заводов. Имеют место следующие функциональные зависимости:
ЦЕХ → ЗАВОД (конкретный цех относится к одному заводу)
ДЕТАЛЬ, ЗАВОД → ЦЕХ (если деталь производят на данном заводе, то только в
одном конкретном цехе).
Очевидно, ключом отношения может быть комбинация (ДЕТАЛЬ, ЗАВОД).
Кроме того, комбинация (ЦЕХ, ДЕТАЛЬ) также подходят на роль ключа.
Следовательно, отношение находится в 3НФ т. к. в случае выбора ключом комбинации
(ДЕТАЛЬ, ЗАВОД), ЦЕХ становится функционально зависимым от этого ключа; в
случае же выбора ключом комбинации (ЦЕХ, ДЕТАЛЬ), наличие функциональной
зависимости ЦЕХ → ЗАВОД ―оправдывается‖ тем, что ЗАВОД – член другого ключа.
Отношение в 3НФ свободно от аномалий добавления и удаления, хотя и может
допускать некоторую избыточность, что впрочем, встречается весьма редко.
Покажем, что отношение, не находящееся в 3НФ, не может быть и в 5НФ. Пусть
R = (J, K, H). K – функционально полно зависит от J, H – прочие поля. По теореме
Хита, из J→K следует R = R[H, J] join R[J, K]. Проекции не имеют общего возможного
ключа. Следовательно, R не находится в 5НФ.
5.11 Нормальная форма Бойса-Кодда (НФБК)
Назовем суперключом такую совокупность атрибутов отношения, которая либо
является ключом, либо включает в себя ключ как подмножество.
Отношение находится в НФБК, если и только если любая функциональная
зависимость между его полями сводится к полной функциональной зависимости от
суперключа.
Определение можно сформулировать и так:
Отношение находится в НФБК, если при наличии функциональной зависимости
X→Y обязательно выполняется требование, что X – суперключ.
Пример:
Рассмотрим отношение V = (МАГАЗИН, ТОВАР, ПРОДАВЕЦ):
МАГАЗИН
ТОВАР
ПРОДАВЕЦ
Привет
Арбуз
Петров
Привет
Банан
Петров
Рябинка
Арбуз
Фролов
Рябинка
Крупа
Юхнов
Это отношение находится в 3НФ. В самом деле, имеются следующие
функциональные зависимости:
МАГАЗИН, ТОВАР → ПРОДАВЕЦ (один и тот же товар в одном и том же
магазине продается одним продавцом).
ПРОДАВЕЦ → МАГАЗИН (один продавец работает только в одном магазине).
Ключами этого отношения могут служить комбинации (МАГАЗИН, ТОВАР) и
(ПРОДАВЕЦ, ТОВАР). А раз так, то оно в 3НФ: первая функциональная зависимость
есть зависимость неключевого атрибута от ключа, а вторая определяет зависимость
члена другого ключа от возможного ключа.
Но оно не в НФБК именно благодаря тому, что в зависимости ПРОДАВЕЦ →
МАГАЗИН, атрибут ПРОДАВЕЦ – не суперключ, а лишь часть одного из ключей.

44
Исходя из этой функциональной зависимости, отношение V можно нормализовать,
разбив его на proj
ПРОДАВЕЦ, МАГАЗИН
V и proj
ПРОДАВЕЦ, ТОВАР
V, каждое из которых уже
находится в НФБК.
Пример:
Возвращаясь к отношению ПРОИЗВОДСТВО (ДЕТАЛЬ, ЦЕХ, ЗАВОД), можем
декомпозировать его в соответсвии с наличием функциональной зависимости
ЦЕХ → ЗАВОД:
Proj
ЦЕХ, ЗАВОД
ПРОИЗВОДСТВО и proj
ЦЕХ, ДЕТАЛЬ
ПРОИЗВОДСТВО .
Покажем, что отношение, не находящееся в НФБК, не может быть и в 5НФ.
Пусть R = (J, K, H). K – функционально полно зависит от J, J – не является возможным
ключом, H – прочие поля. По теореме Хита, из J→K следует R = R[H, J] join R[J, K].
Проекции не содержат общего возможного ключа исходного отношения.
Следовательно, R не находится в 5НФ.
5.12 Многозначная зависимость
Многозначная зависимость подразумевает, что два атрибута (или два множества
атрибутов) независимы друг от друга. Многозначная зависимость (МЗ) возникает между
атрибутами кортежей отношения в ситуации, когда отношение пытается представить
более одной связи типа ―многие ко многим‖. В этой ситуации определенные атрибуты
становятся независимы один от другого и их значения должны присутствовать во всех
комбинациях.
Пример:
Рассмотрим отношение ПОКУПАТЕЛЬ(ИМЯ, АДРЕС, ЛЮБИМЫЙ ТОВАР,
ДИСКОНТНАЯ КАРТА, ДАТА, СУММА). Оно позволяет хранить данные о
покупательских предпочтениях, наличии у покупателей дисконтных карт и адресах
покупателей. Далее представлен экземпляр такого отношения:
ИМЯ АДРЕС ЛЮБИМЫЙ ТОВАР ДИСКОНТНАЯ КАРТА
Иван Металлургов, 99 Колбаса Аккорд
Иван Металлургов, 99 Книги Сократ
Иван Металлургов, 99 Колбаса Сократ
Иван Металлургов, 99 Книги Аккорд
Представим, что атрибут ЛЮБИМЫЕ ТОВАРЫ не зависит от атрибута
ДИСКОНТНАЯ КАРТА. В этом предположении каждый ЛЮБИМЫЙ ТОВАР должен
встретиться в любой комбинации с каждой ДИСКОНТНОЙ КАРТОЙ. Данные в
отношении содержат значительную избыточность. Но она не связана с нарушением
усливий НФБК. В нашей ситуации имеет место зависимость некоторой совокупности
значений из доменов ЛЮБИМЫЙ ТОВАР и ДИСКОНТНАЯ КАРТА от поля ИМЯ.
Наличие многозначной зависимости X→→Y означает, что если 2 кортежа
совпадают в части X, то можно обменять значения компонентов из Y между собой
(при этом оставив нетронутыми оставшиеся атрибуты Z) и получить кортежи из
того же отношения.
В нашем случае имеют место следующие зависимости:
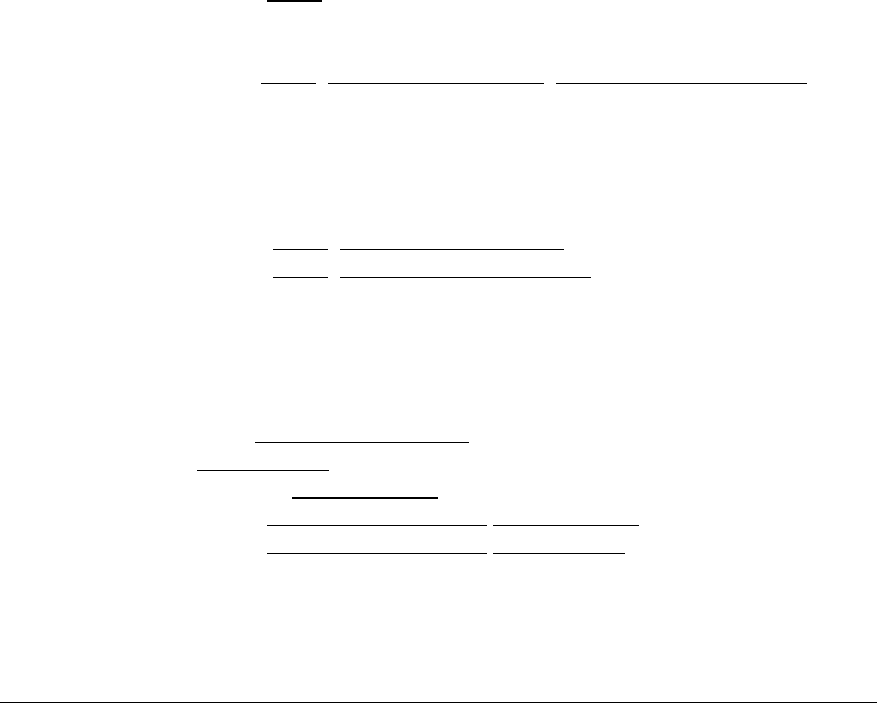
45
ИМЯ → АДРЕС
ИМЯ →→ ЛЮБИМЫЙ ТОВАР
ИМЯ →→ ДИСКОНТНАЯ КАРТА
Всякая функциональная зависимость является частным случаем многозначной
зависимости!
5.13 Четвертая нормальная форма (4НФ)
Отношение находится в 4НФ, если из X→→Y следует что X – суперключ (т. е.
либо является ключом, либо включает в себя ключ).
Данное определение очень похоже на определение НФБК: функциональная
зависимость → заменяется на многозначную зависимость →→. При этом имеется в
виду, что многозначная зависимость X→→Y не тривиальна, т.е. Y не есть
подмножество X и, кроме того, X и Y не образуют вместе все множество атрибутов
отношения.
Соотношение между НФБК и многозначной зависимостью:
Всякая функциональная зависимость есть частный случай многозначной
зависимости;
Поэтому, если отношение в 4НФ, то оно и в НФБК;
Но отношение может быть в НФБК но не быть в 4НФ.
Если отношение не в 4НФ, то его можно декомпозировать, пользуясь теми же
приемами, что и для НФБК.
Пример:
Для отношения ПОКУПАТЕЛЬ выполним декомпозицию на два отношения:
ПОКУПАТЕЛЬ1 (ИМЯ, АДРЕС): здесь единственной зависимостью является
ИМЯ→АДРЕС следовательно Покупатель1 в 4НФ.
ПОКУПАТЕЛЬ2 (ИМЯ, ЛЮБИМЫЙ ТОВАР, ДИСКОНТНАЯ КАРТА).
В отношении ПОКУПАТЕЛЬ2 ИМЯ →→ ЛЮБИМЫЙ ТОВАР и ИМЯ →→
ДИСКОНТНАЯ КАРТА. Наличие двух многозначных зависимостей требует
дальнейщей декомпозиции:
ПОКУПАТЕЛЬ21 (ИМЯ, ЛЮБИМЫЙ ТОВАР)
ПОКУПАТЕЛЬ22 (ИМЯ, ДИСКОНТНАЯ КАРТА).
Ключами являются комбинации каждого из 2 атрибутов, нетривиальных
зависимостей нет, следовательно они в 4НФ. На этом можно остановить процесс
декомпозиции. Правда в целях оптимизации конечное решение стоит несколько
изменить:
ПОКУПАТЕЛЬ1(КОДПОКУПАТЕЛЯ, ИМЯ, АДРЕС)
ДИСКОНТ(КОДКАРТЫ, КАРТА)
ЛЮБИМЫЙТОВАР(КОДТОВАРА, НАЗВАНИЕ)
ПОКУПАТЕЛЬ21(КОДПОКУПАТЕЛЯ, КОДТОВАРА)
ПОКУПАТЕЛЬ22(КОДПОКУПАТЕЛЯ, КОДКАРТЫ)
5.14 Пример проектирования на принципах нормализации
