Seetharaman S. Fundamentals of metallurgy
Подождите немного. Документ загружается.


(for three-dimensional spherical growth):
V
4
3
3
t ÿ
3
7:59
At low transformation fractions, the volume contributed from all grains per
unit total volume is N (nucleation rate):
f
X
V
4
3
N
3
Z
t
0
t ÿ
3
d
3
N
3
t
4
7:60
The nucleation rate (N) has been assumed to be constant. If one considers
impingement, which will slow down the rate,
f 1 ÿ exp ÿ
3
N
3
t
4
7:61
This is known as the Johnson±Mehl±Avrami equation (Porter and Easterling, 1992)
and will result in the classic C-shaped curve when the fraction transformed (f) is
plotted in a diagram with temperature (T) as the y-axis and time (t) as the x-axis. A
schematic of such a diagram, called a TTT-diagram (for time±temperature±
transformation) is shown in Fig. 7.6. The C-shape is caused by a slow nucleation
rate at high T and a slow growth (caused by slow diffusion) at low T.
Phase transformation upon heating
So far the discussion has focused upon phase transformations that occur upon
cooling. The combined nucleation and growth behaviors, resulted in the TTT
type behavior, i.e. the transformation is limited by nucleation at low
undercooling (high temperature) and by growth at low temperatures. Also, the
growth rates themselves have terms for both supersaturation (which increases
with undercooling) and diffusion (which decreases with undercooling). The
resulting rate of transformation vs temperature would then exhibit a maxima. In
7.6 Time±temperature±transformation (TTT) diagram.
286 Fundamentals of metallurgy

the case of heating above a transformation temperature, both the driving force
and diffusion rate increase with temperature. Therefore the effect of increasing
temperature is continuously to accelerate the transformation rate.
Coarsening
In order to lower the total interfacial energy, a multiphase alloy will strive to
shift the size distribution of precipitate s towards as small number of large
precipitates as possible. The rate of this process is strongl y dependent on tem-
perature and, thus, is a concern in high temperature applications and processes.
Depending on the process history, a certain size distribution of the second
phase precipitates will be present in the matrix as a result of nucleation and
growth. The chemical potenti al of solutes in the matrix adjacent to a precipitate
will vary depending on the precipitate±matrix interface curvature due to the
Gibbs±Thomson effect. Therefore there will be a chemical potential difference
between two spherical precipitates of different sizes. This difference will be:
G
RT ln
N
1
N
2
2V
m
1
r
1
ÿ
1
r
2
7:62
As can be seen, the solute concentration will be higher in the matrix near the
smaller particle. As a result, the solute diffuses from the regions adjacent to
smaller particles to the regions near larger ones and the larger particles grow at
the cost of the smaller ones that shrink and eventually disappear altogether. As a
result, the average particle radius r
a
among the particle population increases
with time whereas the total number of particles decreases with time. If diffusion
is the slowest step the rate of coarsening has been found to be (Wagner, 1961):
r
3
a
ÿ r
3
o
kt 7:63
where r
o
is the mean starting radius. k is a kinetic constant that equals
D N
e
, where N
e
is the mole fraction of solutes at equilibrium with very
large precipitates.
Spinodal decomposition
In the discussi on of nucleation and growth of a secon d phase, it was assumed
that a sharp boundary existed between the matrix and precipitating phase. In the
case of spinodal decomposition, the transformation proceeds while maintaining
a coherent and non-di stinguishable boundary.
In the case of spinodal decomposition, the free energy vs composition has a
behavior as that is shown in Fig. 7.7, which is characteristic of a miscibility gap.
Note that, inside the so-called spinodal region, the second derivative of Gibbs
energy is negative. This means that any infinitesimal fluctuation in composition
would lead to an energy decrease for the alloy and would be expected to grow
spontaneously. Let us consider a one-dimensional binary decomposition case in
The kinetics of metallurgical reactions 287
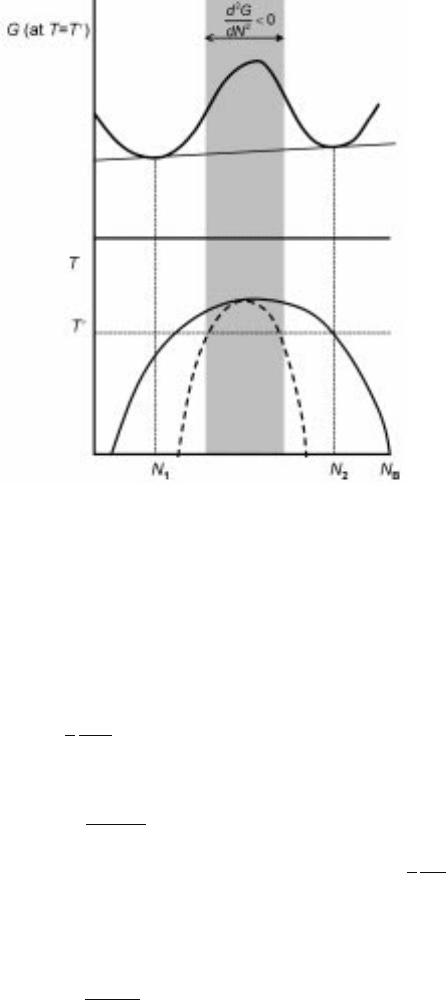
the spinodal region. Sinusoidal fluctu ations may or may not result in
decomposition into two phases as shown in Fig. 7.7. Ba sed on Fick's second
law solution, it can be shown (Cahn, 1968 ) that fluctuations will be stable under
certain condition. A small free energy change can be written as a sum of the
chemical (G
c
), strain (G
s
) and gradient (G
) parts.
The chemical energy is:
G
c
1
2
d
2
G
dN
2
N
2
7:64
The strain energy:
G
s
2
E
1 ÿ
V
m
N
3
7:65
Here E is Young's modulus, is Poisson's ratio and
1
a
da
dN
, where a is the
lattice parameter.
The gradient energy arises due to non-similar nearest neighbors and is thus
related to unlike atom pairs:
G
K
N
2
7:66
Here K is the so-called gradient energy, which depends on the differences in
bond energie s between like and unlike pairs. is the wavelength of the
sinusoidal fluctuation. The total energy change can then be written:
7.7 Free energy vs composition for spinodal decomposition.
288 Fundamentals of metallurgy

G
d
2
G
dN
2
2K
2
2
2
E
1 ÿ
V
m
N
2
2
7:67
Fluctuations will according to this equation be stable when the term within the
brackets is negative. By using a flux equation with a chemical potential gradient
and solving Fick's second law, the kinetics of the decomposition are obtained
(Cahn, 1968) as (after neglecting the non-linear terms):
N N t ÿ N t 0 cos
2
x exp ÿA
2
2
B
2
4
!
t 7:68
Here
A M
@
2
G
@N
2
2
2E
1 ÿ
and
B 2KM=V
m
M is the mobility
M
ND
RT
Ordering
In some binary systems such as Cu-Zn or Cu-Au there is a strong negative
deviation of the activities. This corresponds to a negative enthalpy of mixing. In
general this is indicative of the fact that the components tend to strongly attract
one another. This leads, at low temperatures, where the dis-ordering effect of
entropy and thermal motion is weak, to the formati on of the so-called super
structures. In these structures the atoms organize themselves to maximize the
dissimilar bonds and minimize the similar ones. In general, the ordering
tendency increases with decreasing temperature below a critical temperature T
c
.
The internal energy and enthalpy are continuous across this temper ature and thus
this is a second order transformation. The common mechanism (Porter and
Easterling, 1992) is through nucleation and growth . An ordered region is
referred to as a domain. Both interfacial energy and strain energy are expected to
be low, and therefore nucleation is relatively easy and occurs homogeneously.
Martensitic transformations
Martensitic transformations are brought about by a movement of the interface
between parent and product phases. As the interface advances, atoms in the
parent lattice re-align into the more energetically favorable martensite structure.
The displacement of atoms is relatively small (less than one inter-atomic
spacing) in magnitude and no compositional changes occur. Instead, the atomic
re-alignment results in a shape deformations and a change in symmetry from the
The kinetics of metallurgical reactions 289

original lattice. The martensitic transformation that FCC lattice undergoes to
form a BCT is described by a process called the Bain distortion (Reed-Hill and
Abbaschian, 1992). Since no diffusion is involved, these transformations are
called diffusionl ess. The growth rates of martensite are extremely fast and
approach the speed of sound and therefore nucleation is what primarily controls
the grain size. Nuc leation is thought to occur heterogeneously (Reed-Hill and
Abbaschian, 1992). The interfacial energy is relatively low but the shear
associated with the Bain transformation contributes to an elastic strain energy
that hinders homogeneous nucle ation. The free energy of an ellipsoidal
martensite embryo platelet with radius a and thickness 2c is:
G 2a
2
22 ÿ
81 ÿ
2s=2
2
ac
2
ÿ
4
3
a
2
c G
v
7:69
The second term is the elastic strain energy term where s is the strain, is
Poisson's ratio and is the shear modulus. The most likely heterogeneous
nucleation sites are thought to be dislocations whose strain energy field assists
nucleation. The nucleation energy barrier can be reduced by the dislocation
interaction energy (Porter and Easterling, 1992):
G
d
2s ac
b 7:70
Here b is the burgers vector of the dislocation.
7.4 Gas±solid reactions
Gas±solid reactions, being heterogeneous reactions, occur at phase boundaries,
and thus always accompany the transfer of mass and heat between the reaction
interface and the bulk phase. The overall gas±solid reaction involves a
combination of the following individual steps:
1. Transfer of the gaseo us reacta nts and the gaseous products between the bulk
gas and the external surface of the solid particle.
2. Diffusion of the gaseous reactants and the gaseous products within the pores
of the solid, if the solid contains open porosity.
3. Chemical reaction between the gaseous reactant and the solid at the gas±
solid interface.
4. Transfer of the reaction heat within the solid.
5. Transfer of heat between the external surface of the solid and the
surroundings by convection and radiation.
6. Changes in the structure of the solid due to chemical reaction and heat.
The rate-controlling step can change depending on reaction conditions, and thus
the rate information obtained under a given set of conditions may not be
applicable under another set of conditions. Furthermore, there may not be a single
rate-controlling step because several steps may have comparable effects on
determining the overall rate. The relative importance of these steps could also
290 Fundamentals of metallurgy
change in the course of the reaction. Therefore, understanding how the individual
reaction steps interact with each other is important in determining not only the
rate-controlling st ep under given reaction conditions but also whether more than a
single step must be considered in expressing the rate over the entire duration of the
reaction. The treatments of the above individual component steps were discussed
in Section 7.2 Fundamentals of heterogeneous kinetics on page 270.
Because the transfer of mass and, to a lesser extent, heat constitutes an
important aspect of a gas±solid reaction, the quantitative analysis of the overall
rate must necessarily take into account the geometry and structure of the solid
before, during, and after the reaction. Although there are other types of gas±solid
reactions, the most important group of reactions in metallurgical and materials
processing operations consists of those in which a solid reacts with a gas to
produce a coherent layer of porous products. Therefore, this section will mainly
be concerned with this type of reaction, which is given by equation 7.1. For the
analysis of other types of gas±solid reactions, the reader is referred to other
references (Szekely et al., 1976).
7.4.1 Reaction of an initially non-porous solid producing a
porous product layer
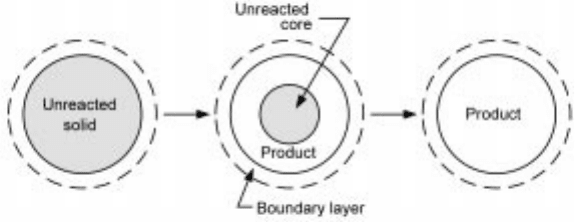
In this type of gas±solid reaction, the reaction progresses in a topochemical
manner from the outer surface of the solid towards its interior, as depicted in
Fig. 7.8. The reac tion forms a coherent porous produc t (or ash) layer around the
unreacted portion of the solid, with the chemical reaction taking place at the
sharp interface between the two zones. This shrinking-core picture has been
applied to a wide range of reactions. Szekely et al. (1976) generalized the results
of many previous investigators on reactions that are isothermal and of first order
with respect to the gaseous reactant. They formulat ed the following equation
incorporating chemical kinetics, diffusion through porous product layer, and
external mass transfer, as well as the three basic geometries of the solid:
g
F
p
X
2
s
p
F
p
X 4X =Sh
t
7:71
7.8 Reaction of an initially non-porous solid that forms a coherent layer of
porous product (the shrinking-core reaction system).
The kinetics of metallurgical reactions 291

where F
p
is the shape factor ( 1, 2, or 3 for a slab, a long cylinder, or a sphere),
and
t
bk
B
B
A
p
F
p
V
p
C
Ab
ÿ
C
Cb
K
t 7:72
2
s
k
2D
eA
V
p
A
p
1
1
K
7:73
Sh
D
A
:d
p
D
eA
D
A
D
eA
k
mA
d
p
D
A
D
A
D
eA
Sh 7:74
g
F
p
X 1 ÿ 1 ÿ X
1=F
p
7:75
and
p
F
p
X X
2
for F
p
1 7:76a
X 1 ÿX ln 1 ÿ X for F
p
2 7:76b
1 ÿ 31 ÿ X
2=3
21 ÿ X for F
p
3 7:76c
It has been shown (Szekely et al., 1976) that chemical reaction controls the overall
rate when
2
s
< 0:1 or 0.01 depending on the range of tolerable error (<10% or
<1%, respectively). On the other hand, pore diffusion and external mass transfer
control the overall rate (g
F
p
X becomes negligible) when
2
s
> 10 or 100.
Individual forms of equation 7.71 were used for various metallurgical
reactions (Lu and Bitsianes, 1968; Seth and Ross, 1966; St. Clair, 1965;
Themelis and Gauvin, 1963; Kawasaki et al., 1963; McKewan, 1960). Sohn and
Sohn (1980) subsequently showed that the right-hand sides of equations 7.76a to
7.76c can be derived as a single combined term given by
p
F
p
X 1 ÿ
F
p
1 ÿ X
2=F
p
ÿ 21 ÿ X
F
p
ÿ 2
; 7:77
conversion function for
pore-diffusion control
p
2
X for a long cylinder can be obtained by applying L'Hospital's rule to the
right-hand side of equation 7.77, resulting in the familiar expression given by
equation 7.76b.
The effect of changing particle size due to the difference in the volumes of the
reactant and the product solids can be incorporated by redefining p
F
p
X as
follows, if one neglects the change in the mass-transfer coefficient with the small
change in particle size in the last term of equation 7.71 (Szekely et al., 1976):
p
F
p
X zX
2
for F
p
1 7:78a
Z ÿ Z ÿ 11 ÿ X ln Z ÿ Z ÿ 11 ÿ X
Z ÿ 1
1 ÿ X ln 1 ÿ X for F
p
2 7:78b
292 Fundamentals of metallurgy
3
Z ÿ Z ÿ Z ÿ 11 ÿ X
2=3
Z ÿ 1
ÿ 1 ÿ X
2=3
( )
for F
p
3 7:78c
where Z is the volume of the product solid formed from unit volume of the
reactant solid. It can be shown (Sohn, 1980) that the right-hand sides of
equations 7.78a to 7.78c (and those of equations 7.76a to 7.76c as special cases)
can be derived as a single term given by
p
F
p
X
F
p
F
p
ÿ 2
Z ÿ Z ÿ Z ÿ 1 1 ÿ X
2=F
p
Z ÿ 1
ÿ 1 ÿ X
2=F
p
( )
7:79
The expressions of p
F
p
X for Z 1 and/or F
p
2 can again be obtaine d by
applying L'Hospital's rule.
When there is a substantial change in the gas volume upon reaction, Sohn and
Sohn (1980) obtained the following approximate solution to replace equation
7.71:
t
g
F
p
X
2
s
ln 1
p
F
p
X
41 X
Sh
7:80
where
ÿ 1C
Ab
=C
T
7:81
Sohn and Szekely (1972a) analyzed the system in which the reaction order with
respect to the gaseous reactant is different form unity. In many gas±solid
reactions, substantial enthalpy changes accompany the reactions. Such non-
isothermal systems are more difficult to analyze than the isothermal systems
discussed above, and may exhibit multiple stead states and thermal instability.
These aspects have been reviewed elsewhere (Szekely et al., 1976).
The shrinking-core model is attractive for its conceptual and mathematical
simplicity. It should be noted, however, that its validity is limited to the
reaction of a non-porous solid occurring at a well-defined sharp reaction
interface. In general, the improper application of the shrinking-core model to
the reaction of a porous solid results in an erroneous analysis of experimental
data. Thus, one may obtain incorrect dependence of the rate on reaction
conditions and physical parameters such as temperature, gaseous reactant
concentration, and particle siz e. The proper analysis of the reac tion of porous
solids is discussed below.
7.4.2 Reaction of a porous solid
Many solid reactants have some initial porosity, allowing diffusion and chemical
reactions to occur simultaneously in a diffuse zone. The progress of reaction in a
porous solid is illustrated in Fig. 7.9. Reaction takes place throughout the
particle or pellet volume, and the concentration of the gaseous reactant decreases
The kinetics of metallurgical reactions 293
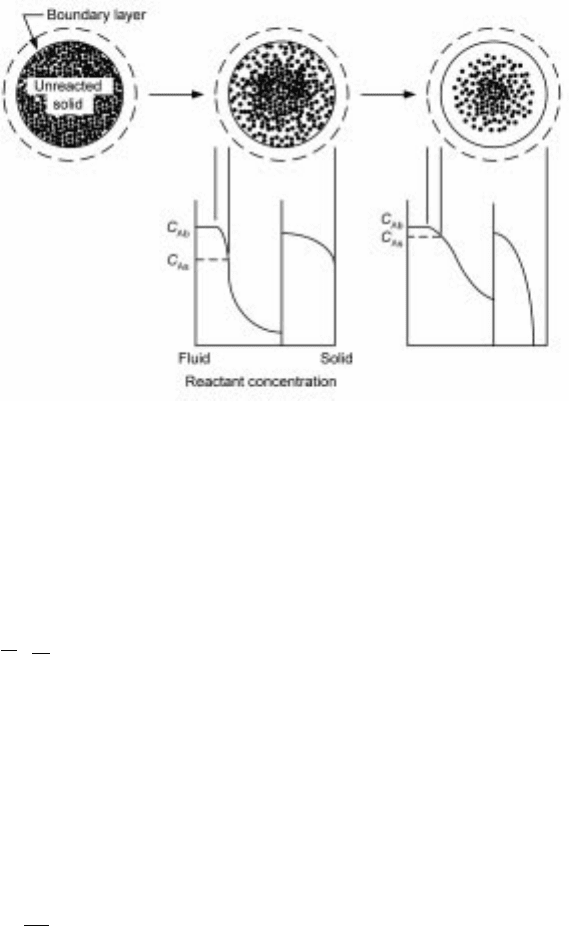
as it diffuses into the interior of the particle while reacting on its path. The
reaction given by equation 7.1 taking place in a porous solid can be described
mathematically by formulating the conservation equations for the gaseous and
the solid reactants, and for energy if substantial heat effect is involved.
The conservation of gaseous species per unit volume of the pellet (including
the pore space) is given by
r N
i
R
i
; i A or C 7:82
This equatio n incorporates the pseudo-steady-state approximation, which states
that the accumulation term can be neglected for gas±solid reactions (Bischoff,
1963; 1965; Luss, 1968).
For many hete rogeneous reactions, the molar rate of consumption of the
gaseous reactant per unit area of the reaction interfaces is given by the
Langmuir±Hinshelwood rate equation, discussed earlier and expressed by
equation 7.2.
The molar rate of consumption of the solid reactant per unit volume of the
solid is expresse d by
B
@w
@t
bÿ
_
m
A
S
v
bÿ
_
m
A
S
o
v
f w 7:83
where w is the local fractional conversion of the solid reactant, S
o
v
is the initial
surface area per unit volume of the solid, and f w represents the relative
variation of the specific surface area S
v
with solid conversion.
The fluxes of g aseous species, N
i
, must, in general, be related to
concentrations through the Stefan±M axwell equations (Eddings and Sohn,
1993; Szekely et al., 1977; Szekely and El-Tawil, 1976). However, for a binary
7.9 Reaction of an initially porous solid.
294 Fundamentals of metallurgy

mixture or by using an effective binary diffusivity, one may use the simpler
relationship given below:
N
i
ÿC
T
D
ei
rx
i
x
i
X
n
j1
N
j
7:84
The rate of production of gaseous species i per unit volume, R
i
, is related to the
rate of reaction of the solid reactant through stoichiometry, as follows:
R
A
B
B
b
@w
@t
ÿ
B
_
m
A
S
o
v
f w 7:85a
R
C
c
B
B
b
@w
@t
c
B
_
m
A
S
o
v
f w 7:85b
When the solid temperature changes during the reaction, the conservation of
energy is described by
c
p
@T
@t
ÿ
r q ÿH ÿR
A
7:86
The simultaneous solution of equations 7.82, 7.83 and 7.86 with appropriate
boundary conditions yields the profiles of the gaseous species concentrations as
functions of position inside the solid. Using these concentration profiles, the
local conversion of solid, w, can be obtained as a function of time by solving
equation 7.83 together with equation 7.2. The overall conversion X is then
calculated by integrating the local conversion over the entire solid volume.
Closed-form solutions to the governing equations have been obtained for
certain special cases. When the reaction involves a substantial heat effect, these
equations must in general be solved using a numerical technique. Even in such a
case, the conver sion-vs-time relationship for a diffusion-controlled irreversible
reaction (K ! 1) is given by equation 7.71 or 7.80 without the g
F
p
X term.
Various models for a reaction between a porous solid and a gas have been
formulated, the differences among which are largely equivalent to the use of
different dependences of rate on solid conversion, f w.
The grain model
This model assumes that the porous solid is made up of small non-porous grains
of a uniform size that each react according to the chemical-reaction-controlled
shrinking-core scheme discussed above (Szekely et al., 1976; Sohn and Szekely,
1972b; Szekely and Evans, 1970). This picture, although rather unrealistic and
restrictive, provided an early basis for the incorporation of solid structure in
analyzing gas±solid reactions. Furthermore, the analysis of this system also
provided us with the foundation for more realistic and less restrictive descrip-
tions of gas±solid reactions in the subsequent work, as will be discussed later.
The generalized grain model developed by Sohn and Szekely (1972b), which
encompasses many other specific models to represent similar configurations
The kinetics of metallurgical reactions 295
