Seetharaman S. Fundamentals of metallurgy
Подождите немного. Документ загружается.

Transmission methods
The absorption coefficient can be determined by using a spectrophotometer to
measure the i ntensities of the incident (I
o
) and emerging beams after
transmission through a sample of known thickness (d).
33,102
I I
o
exp (ÿ*d) (4.21)
In solids the extinction coefficient (E) is measured sinc e radiation can be
scattered by crystallites, grain boundaries, particles, etc .
E * s* (4.22)
where s* scattering coefficient.
Reflectance methods
Absorption coefficients have been determined from measurements of trans-
mittance and reflectance.
33,103
4.6 Properties related to mass transfer
4.6.1 Diffusion coefficient (D)
There are several types of diffusion coefficient.
Self diffusion involves the movement of various species present in the melt
by random motions. There is no net flux of any species and no chemical
potential gradients within the melt. It is also customary to quote self-diffusion
values for impurity diffusion but which is strictly chemical diffusion since a
concentration gradient is produced.
Tracer diffusion is essentially the same process as self-diffusion but some of
the species are radioactive. Consequently, there is a net flux and chemical
potential; but this gradient refers solely to the radioactive species.
Chemical diffusion is the movement of a species in the melt in response to a
gradient of chemical potential arising as a result of either concentration or
temperature gradients in the melt. Diffusion occurs in a direction that results in a
reduction of the concentration gradient. Chemical diffusion in response to a
temperature gradient is referred to as Soret diffusion.
When diffusion involves the movement of two or more species it is referred
to interdiffusivity. For example, if the cation is more mobile than the anion an
electrical field is established which retards the cation and enhances the anion
mobility in order to prevent a space charge being established in the melt.
Fick's first and second laws apply for single component diffusion
J ÿD (dC/dy) (4.23)
dC/dT D (d
2
C/dy
2
) (4.24)
146 Fundamentals of metallurgy
where J is the flux across a plane, (dC/dy) is the concentration gradient, D is the
diffusion coefficient, and t is the time. The average value of the square of linear
displacement (d) of a species after time t is given by
d
2
2Dt (4.25)
The temperature dependence of the diffusion coefficient is usually expressed as
an Arrhenius relation:
D D
o
exp (ÿE
D
/R*T) (4.26)
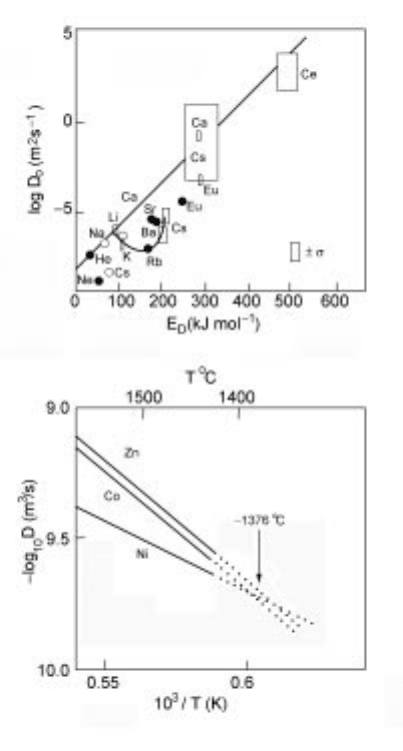
4.15 Relation between log
10
D
0
and (a) activation energy for diffusion of
various impurities in solid obsidian
104
and (b) reciprocal temperature for Co,
Ni and Zn in CaO.MgO.2SiO
2
.
105
Measurement and estimation of physical properties of metals 147
where D
o
is a constant and E
D
is the activation energy for diffusion. These
parameters D
o
and E
D
are inversely proportional to one another (Fig. 4.15a) and
this is known as the compensation effect. It is the diffusion equivalent to
Urbain's assumption regarding the relation between A and E
for viscosity. One
effect of the compensation rule is that diffusion coefficients for different species
tend to come to a common value (Fig. 4.15b) at a specific temperature (around
1650K in Fig. 4.15b).
Methods
7,106±108,33
In the capillary reservoir method the sample containing the solute to be studied
is contained in a capillary tube (of uniform diameter and known length) with one
end sealed. The capillary is then immersed in a large container holding the
solvent sample. The capillary tube is removed after a set time and the
concentration in the capillary tube determined. Convection is minimised because
of the small diameter of the capillary.
In the diffusion couple method a long capillary of known cross-section is
half-filled with the solvent and the solute samples. The capillary is then rapidly
heated to the required temperature and maintained at this temperature for a
specific time and is then quenched. Diffusion coefficients c an then be
determined by determining solute concentrations at various positions along
the specimen. One difficulty is that some diffusion may occur during the heating
and cooling periods.
The shear method avoids the problems by only aligning the samples at the
start of the run and then misaligning the samples at the end of the measurement
period. It has not been used for high-temperature measurements.
In the instantaneous plane method the solute is in the form of a thin disc and
while the solvent consists of a long thin specimen. At the start of the experiment
the thin disc disperses into the solvent sample.
The elec tro chemical method has the adva ntage that time-consuming
chemical analysis is replaced by measurements of current and voltage. However,
it cannot be applied to some systems.
Rayleigh scattering has been used to measure diffusion coefficients in
liquids at room temperatures; this techniq ue has the advantages of being a non-
contact method and is very rapid.
109
Electro-magnetic fields have recently been used to minimise contributions
from convection to the diffusion coefficient.
110
4.7 Estimating metal properties
It is apparent from the above text that the accurate measurement of thermo-
physical properties at high temperatures is both time-consuming and requires
considerable expertise. Furthermore, process control often requires a rapid input
of data for the relevant properties of the materials involved, for instance how
148 Fundamentals of metallurgy
much CaO must be added to a coal slag to obtain a viscosity where the slag can
be poured from the reaction vessel. Thus it is not surprising that models or
routines have been developed to estimate the properties from the chemical
composition, for this is frequently available on a routine basis. Many models
have been reported in the literature. This review does not claim to cover all these
published models but covers only the models and routines with which the author
has used or tested or which have come to his notice.
The partial molar method is a simple method that has proved very useful for
estimating some physical properties for alloys and slags. Using the case of a
property (P) of an alloy, the value can be calculated from the sum of the product
of the (mole fraction the property value) for each constituent of the alloy. The
partial molar property for each constituent is denoted
P.
P
X
X
1
P
1
X
2
P
2
X
3
P
3
X
4
P
4
4:27
where X mole fraction and 1, 2, 3, 4 denote the different components.
However, some properties (such as viscosity) are very dependent upon the
structure of the alloy or slag and in these cases the structure has been taken into
account. Consequently, the partial molar method is particularly effective in
estimating those properties which are least affected by structure (e.g. Cp and
density).
4.7.1 Estimation of C
p
and (H
T
ÿ H
298
)
The heat capacity±temperature relation for solid materials (alloys and slags) can
be represented in the form:
Cp a bT ÿ (c/T
2
) (4.28)
Integration of Cp dT between 298K and the temperature of interest, T gives
Z
T
298
Cp dT H
T
ÿ H
298
aT b=2T
2
c=T d 4:29
where d contains all 298K terms. The values of the constant a for the alloy or
slag can be calculated by:
a
X
X
1
a
1
X
2
a
2
X
3
a
3
X
4
a
4
::: 4:30
Thus the constants b and c can be calculated in a similar way so the Cp and
enthalpy for the solid can be calculated for any required temperature.
The heat capacity of the liquid is usually assumed to be constant, i.e.
independent of temperature and consequently values for Cp of the alloy can be
calculated from equation 4.27 where
P
1
,
P
2
, etc. are the Cp values of liquid for the
various components. The only parameter now required is the enthalpy of fusion
fus
H. This can be calculated in a similar way for the entropy of fusion,
fus
S
which represents the disorder which occurs when a solid transforms to a liquid.
Measurement and estimation of physical properties of metals 149
fus
H T
liq
:
fus
S 4:31
Thus it is necessary to have a value for the liquidus temperature (T
liq
) or have an
estimated value. The enthalpy of fusion can then be calculated by the relation:
fus
S
X
X
1
fus
S
1
ÿ
X
2
fus
S
2
X
3
fus
S
3
. . . 4:32
The enthalpy for a temperature, T, where the liquid is the equilibrium phase can
be calculated from
H
T
ÿ H
298
Z
T
liq
298
Cps dT T
liq
fus
S
Z
T
T
liq
Cpl 4:33
This method works well for alloys and sla gs and the estimated values for the
most part lie within 2 to 5% of the measured values.
Problems
·
The above approach does not take into account any solid state transitions
which might occur (such as those occurring in steels, Ni-based superalloys
and Ti-alloys). Although the (H
T
ÿ H
298
) values will be slightly low in the
transition ranges the values of (H
T
ÿ H
298
) for the liquid will not be affected
since the entropy change can be considered as a small step in the disordering
associated with the change from a fcc or cph solid to a liquid.
· With glasses there is a transition from a glass to a supercool ed liquid at the
glass transition temperature (T
g
) and this is accompanied by a step increase
(C
p
) in C
p
of about 30% (and a threefold increase in ). The C
p
±T relation
can be mode lled
18
by assuming that the C
p
for the supercooled liquid and
liquid region remains constant and that there is no enthalpy of fusion
involved.
· Another weakness of the approach outlined above is that it assumes that the
fusion process occurs at a discrete temperature (T
liq
) whereas in practice it
occurs over a melting range.
·
Another difficulty with the partial molar method lies in the fact that some
alloys, (e.g. Ni-based superalloys) contain components such as Al (mp 933K)
and W (mp 3695K) with melting points far away from the T
liq
of the alloy
(circa 1720K). This raises a question of whether the property values used in the
calculation should be (i) the property value at the melting point (
P
m
) or (ii) the
property value extrapolated to 17 20K. The value at the melting point (
P
m
) can
be adopted because it is considered that this was the point when all the atoms
(including the Al and W) become disordered. Recent evidence on the densities
of superalloys indicates that no serious errors are caused by this assumption.
36
The values calculated with the partial molar approach are usually within 2±5%
of measured values (which are themselves subject to experimental
unc ertainties). Comm ercial thermodynamic p ack age s such as MTDATA,
Thermocalc and FACT are available . These packages are capable of predicting
150 Fundamentals of metallurgy

solid state transitions and the melting range and their associated enthalpies.
125
Furthermore, the fraction liquid can be calculated through the Scheil
equation.
125
Consequently, where a high degree of accuracy is required, Cp
and enthalpies should be calculated with these packages
4.7.2 Density () molar volume (V)
The structure of the melt does not have a large effect on the density of the alloy
or slag. The density can be calculated from molar volume:
V M/ (4.34)
where M molecular mass of the sample ( x
i
M
i
) and the molar volume can
be calculated from the partial molar volumes of the constituents:
V
X
X
1
V
1
X
2
V
2
X
3
V
3
X
4
V
4
. . . 4:35
The substitution of density for molar volume in equation 4.35 results in only a
small error. The temperature dependence of the volume is calculated from the
partial molar (volume) thermal expansion coefficients (usually 3 where
is the linear thermal expansion coefficient).
dV=dT
V
X
X
1
1
ÿ
X
2
2
X
3
3
. . . 4:36
The linear thermal expansion coefficient () of a glass or slag can be calculated
with the model due to Priven
126
or using the relation due to Yan et al.
155
10
6
(K
ÿ1
) (293±573K) ÿ18.2 48.9
cor
) where
cor
is the optical basicity
corrected for charge balancing of Al
3+
.
Density±temperature relations for the solid state can then be calculated from
the molar volumes (or densities) of the solid at 298K and the thermal expansion
coefficients. Similarly, values of density of liquids as a function of temperature
can be calculated from
V
m
and
for the constituents in the liquid states .
However, the density is affected slightly by the structure of the melt. As we have
seen in the section `Methods of determining structure' on p. 118, one way of
accounting for the effect of structure is through the use of thermodynamics.
Take, for example, the densities of superalloys, values calculated from partial
molar volumes are consistently 2±5% lower than measured values and the
shortfall increases with increasing Al content. The chemical activities of the
constituents in the Ni-Al system show marked negative departures from Raoult's
law (i.e. the atoms like each other). This results in tighter bonding and decrease
in molar volume (V
xs
) or an increase in density (
xs
) of the melt. Since the
effect of structure on the molar volume is relatively small it can be accounted for
by adding (V
xs
) to rquation 4.35. In the case of Ni-superalloys, V
xs
can be
expressed in terms of the Al content (K(% Al), where K is the correction term)
without much loss in accuracy.
Measurement and estimation of physical properties of metals 151
In a similar manner the activities of the CaO-SiO
2
system show negative
departures from Raoult's law. Correction terms in this case were determined by
back-calculating the parameter (X
i
V
1
) as a function of SiO
2
content from
measured molar volumes of melts containing CaO and SiO
2
and could be
accounted for by the relation,
V
SiO
2
(19.55 7.97X
SiO
2
) 10
6
m
3
mol
ÿ1
.
Similar relations are used for determining the effects of Al
2
O
3
(
V
Al
2
O
3
(28.3
32X
Al
2
O
3
ÿ 31.45X
2
Al
2
O
3
) 10
6
m
3
mol
ÿ1
) and P
2
O
5
(65.7 10
6
m
3
mol
ÿ1
).
In most cases the values calculated using these corrections are within 2%
(and nearly always within 5%) of the measured values. If more accuracy is
required the use of thermodynamic packages such as MTDATA,
126
Thermocalc
and FACT are recommended.
Details of published models for calculating densities of alloys and slags are
given in Table 4.4.
4.7.3 Viscosity ()
The approaches taken to calculate the viscosities of liquids fall into two
classes:
129
1. by treating the liquid as a dense gas;
130
2. by assuming the liquid structure is similar to that of the solid except that it
contains holes (e.g. Frenkel,
131,132
Weymann,
133
Eyring
134
and Furth
135
).
In the Weymann±Frenkel approach the atoms are in thermal oscillation but for
them to move from their present position into another equilibrium position it is
necessary that (i) their energy should be greater than the activation energy
required to move from site 1 to 2 and (ii) the next position shoul d be empty (i.e.
the site of a hole). Thus viscosity can be calcul ated from the probabilities that
molecule can (i) jump from one position to another and (ii) find a `hole' in the
liquid. Weymann
133
derived the following equation:
(kT/*)
0.5
{(2kmT)
0.5
/(v
0.667
P
v
) exp (*/kT) (4.37)
where k Stefan Boltzmann constant, * is the height of potential barrier
(associated with activation energy for viscous flow) m and v are the mass and
volume of the structural unit and P
v
is the probability of finding the next
equilibrium site empty.
The biggest drawback in developing reliable models for the viscosities of
molten alloys and slags (and glasses ) lies in the experimental uncertainties in the
experimental data (see the section `Slags' on p. 154). For instance, Iida and
Guthrie
7
plotted the reported values for molten Fe and Al and showed that these
values varied by 50% and 100%, respectively, around the mean (although
the lower values are more likely to be correct unless the crucible is non-w etting
to the melt). Thus with uncertainties of this magnitude it is difficult to determine
whether factors such as atom radius or structural eff ects are influencing the
152 Fundamentals of metallurgy

Table 4.4
Details of models to calculate densities of alloys and slags
Reference System Details of Method
Uncertainty
Mills
et al.
127
Alloys
1. Solids
:
298
= (X
1
298
)
1
+ (X
2
298
)
2
+ (X
3
298
)
3
+ . . .
2%
(d/dT) = X
1
(d/dT)
1
+ X
2
(d/dT)
2
+ X
3
(d/dT)
3
+ . . .
T
=
298
+ (T ÿ
298K) (d/dT) Correction needed when Al
> 1% e.g. Ni-alloys
2. Liquids: V
m
= X
1
V
1
m
+ X
2
V
2
m
+ X
3
V
3
m
+ . . .
2%
2. V
ÿ V
xs
= X
1
1
+ X
2
2
+ X
3
3
+ . . . where
= (1/V)(dV/dT)
V
T
= V
m
(1+ (T
ÿ T
m
)) and
V
xs
= V + K (% Al) for Ni alloys with Al
Sung
et al.
113
Ni-based Numerical analysis of measured data:
(%) = b
0
+ b
1
(T ÿ T
R
) + b
2
(T ÿ T
R
)
2
+ b
3
(T ÿ T
R
)
3
2%
alloys where b
o
, b
1
, b
2
, b
3
and T
R
are constants: values given for various elements
2. V ÿ V
xs
= X
1
V
1
+ X
2
V
2
+ X
3
V
3
+ . . .
3. V
xs
= ÿ1.50 + 4.5X
Al
+ 5.2(X
Cr
+ X
Ti
) + 0.43(X
W
+ X
Re
+ X
Ta
+ X
MO
)
Robinson
et al.
125
Alloys 1. Use of thermodynamic software to predict, V an
d data stored for different
<2%
phases of alloy: e.g. steels
=
Fe
+ k
1
C
1
where k is effect of different solutes and C = %
2. Values calculated for different phases
Bottinga and Slags V =
X
1
V
1
+ X
2
V
2
+ X
3
V
3
Values of V given
2±3%
Weill
128
Corrections to V values for compositions of Al
2
O
3
, Na
2
O, K
2
O, CaO, MgO, FeO:
equations for
also corrected for chemical compositions of these oxides
Mills and Slags
Method 1:
(kgm
ÿ3
) = 2460 + 18 (% FeO + % Fe
2
O
3
% + % MnO + % FeO)
5%
Keene
18
Method 2:
V = X
1
V
1
+ X
2
V
2
+ X
3
V
3
+ . . . at 1773K V (10
ÿ6
m
3
mol
ÿ1
) values for:
2%
CaO = 20.7; FeO = 15.8; Fe
2
O
3
= 38.4: MnO = 15.6; MgO = 16.1; Na
2
O = 33; K
2
O = 51.8;
TiO
2
= 24; P
2
O
5
= 65.7; SiO
2
= (19.55 + 7.97X
SiO
2
) Al
2
O
3
= (28.3 + 32X
Al
2
O
3
ÿ 31.45X
2
Al
2
O
3
)
(dV/dT) = 0.01%K
ÿ1
Robinson
et al.
125
Slags Use of thermodynamic software: Molar volumes s
tored for oxides and correction based
2%
on molar Gibbs energy of system
Hayashi and Slags V/
X
1
V
1
= (K
mix
H/R*T) where is the relative integral enthalpy of mixing (deter
mined with 2%
Seetharaman
147
thermodynamic software) and K = constant
Priven
126
Glasses Solids: V =
X
1
V
1
+ X
2
V
2
+ X
3
V
3
V Values and range of applicability given.
Special procedures for boro-silicates
viscosity. Similarly, the uncertainties associated with the measurements of slag
viscosities are probably around 25% although these uncertainties can be
reduced to < 10% where best practice is observed. Structure has a marked
effect on viscosity. The effect of structure is much more pronounced in glasses
and slags than in alloys because of the polymeric nature of the structure of
glasses and som e slags.
The Arrhenius equation is widely used for expressing the temperature
dependence of viscosity:
ln ln A
A
B
A
/T (4.38)
where B
A
E/R* and A
A
is a pre-exponential term, E
A
is the activation energy
and R* is the gas constant. Equation 4.39 above reduces to equation 4.40. The
Weymann relation is thought to provide a slightly better fit of experimental
viscosities than the Arrhenius relation
A
W
T exp (B
W
/T) (4.39)
or
ln (/T) ln A
W
B
W
/T (4.40)
where B
w
E
W
/R* and A
W
is a pre-exponential term, E
W
is the activation energy.
Slags, glasses
In glasses the liquid transforms on cooling to a supercooled liquid and the
viscosity exhibits a smooth relationship with temperature all the way to the glass
transition temperature (T
g,
which occurs when log
10
(Pas) 12.4). The Vogel±
Fulcher±Tammann (VFT) relation (derived from the free volume theory
136
) is
frequently used to express the relation between viscosity and temperature for
glasses and has the form:
ln ln A
V
B
V
/(T ÿ T
o
) (4.41)
Many models for calculating the viscosities of slags and glasses have been
reported;
137±150
details are given in Tables 4.5 and 4.6; information on another
15 models is given by Kondratiev.
129
Several approaches have been adopted in
the models to take the structure of the melt into account, namely:
1. By carrying out a numerical analysi s of experimental data.
2. By relating viscosity to structural parameters (such as NBO/T or optical
basicity) which provides a measure of the structure.
3. By using thermodynamic parameters as a measure of structure.
4. By using molecular dynam ics to calculate the number of bridging (N
Oo
) non-
bridging (N
O-
) and free oxygens (N
O
2
-
) and relating these to the viscosity.
The reported models for estimating the viscosities of slags, glasses and alloys
are given in Tables 4.5, 4.6 and 4.7, respectively.
154 Fundamentals of metallurgy

Table 4.5
Details of published models for the estimation of slag viscosities
Reference Slag type T- Details of model and c
omments
Slag
%
depen-
dence
Riboud
et al.
137
Various Wey A
W
; B
W
functions of 5 groups `CaO' + `SiO
2
' + `Al
2
O
3
' + `CaF
2
' + `Na
2
O' Mould 30
where X
`CaO'
contains X
CaO
+ X
MgO
+ X
FeO
+ X
MnO
etc.
flux
ln A = ÿ19.81 + 1.73 X
CaO
+ 3.58 X
CaF
2
+ 7.02 X
Na
2
O
ÿ 35.76 X
Al
2
O
3
B = 31140
ÿ 23896 X
CaO
ÿ 46356 X
CaF
2
ÿ 39159 X
Na
2
O
ÿ 68833X
Al
2
O
3
Works well (30%) for variety of slags
Urbain
138
Various Wey A
W
; B
W
functions of 3 groups
Various 25
Glass formers: X
G
= X
SiO
2
+ X
P
2
O
5
Amphoterics X
Al
= X
Al
2
O
3
+ X
B
2
O
3
+ X
Fe
2
O
3
Modifiers: X
M
= X
CaO
+ X
MgO
+ X
Na
2
O
+3 X
CaF
2
+ X
FeO
+ X
MnO
+ 2X
TiO
2
+ B
W
= B
0
+ B
1
X
G
+ B
2
X
G
2
+ B
3
X
G
3
and Bi =
I + bi + ci
i
2
ln Aw = 0.2693B
W
+ 11.6725 Special Bw values for MnO, MgO
Iida et al.
139
Many Arr
(Pas) = A
0
exp (E/Bi) where
0
is viscosity of hypothetical network- Mould 25
forming melt and Bi = basicity index E = 11.11
ÿ 3.65 x10
ÿ3
T and
flux
a = 1.745
ÿ 1.962 10
ÿ3
T + 7
10
ÿ7
T
2
and Bi =
(i %i)
B
/(
i
%
I
)
A
where A = acid oxides and B = basic oxides or fluorides:
= 1.8
10
ÿ7
BF 19
(M = iT
m
)
0.5
exp (H
i
/RT
m
)/V
)m
0.667
exp (H
i
/RT
m
) where H
i
= 5.1 T
m
and
values of
given
Senior
140
Coal Wey A = a
0
+ a
1
B + a
2
(NBO/T) where a
0
= 2.816 a
1
= 0.4634: a
2
= 0.3534
(NBO/T) = X
CaO
+ X
MgO
+ X
Na
2
O
+ X
FeO
+ X
MnO
ÿ X
Al
2
O
3
+ X
Fe
2
O
3
/
{0.5(X
SiO
2
+ X
TiO
2
) +X
Al
2
O
3
+ X
Fe
2
O
3
}
Equations also given for low temperatures
