Щипицын А.Г., Кощеев А.А., Алешин Е.А., Павловская О.О. Элементы прикладной теории надежности
Подождите немного. Документ загружается.


Рис. 2.1. Функция надежности
0
t
1
P(t)
Основные свойства функции P(t):
1) P(0) = 1;
2) P(∞) → 0;
3) P(t
2
) ≤ P(t
1
) при t
2
> t
1.
Функция надежности имеет следующие очевидные свойства (вытекающие из
свойств функции ):
()
tQ
1)
– полагаем, что в начальный момент времени (момент включе-
ния) элемент исправен;
()
10 =P
2)
– элемент не может работать сколь угодно долго;
()
0→∞P
3)
– монотонно убывающая функция, т. е.
()
tP
(
)()
1212
при , tttPtP >≤
, что
вполне естественно, ибо надежность работы элемента с течением времени не воз-
растает (но может быть постоянной).
Функцию можно приближенно найти из опыта. Предположим сначала,
что нам нужно найти значение этой функции при
()
tP
T
t
=
, т. е. вероятность безот-
казной работы за временя
T. Поставим на испытание N одинаковых элементов и
испытываем их в одинаковых условиях время
T. Пусть к моменту T не отказало n
элементов из
N. Тогда отношение
()
TP
N
n
*
= есть частота появления события, со-
стоящего в безотказной работе элемента, и по теореме Бореля с вероятностью
единица
() ()
TP
N
n
TP
*
→=
∞
→
N
при .
Практически при достаточно больших
N
()
TP
N
n
≈ .
(
)
tP
T
t
≤
Если мы хотим найти функцию
для всех значений , то необходимо
фиксировать моменты возникновения отказов элементов, а затем построить эмпи-
рическую функцию надежности
()
(
)
N
tn
tP
N
= . Очевидно, что это кусочно-
постоянная функция, имеющая скачки на величину
N
1
в момент каждого отказа.
При увеличении
N эта функция равномерно приближается к функции
(
)
tP и при
больших
N имеет место приближенное равенство
(
)(
tPtP
N
)
≈
.
11

[
]
T ,0,
Важно отметить, что если испытания проводить на интервале времени
то за границами интервала мы ничего сказать о функции не можем, т. е. в
общем случае ее нельзя экстраполировать. Правда, иногда из физических сообра-
жений или из предыдущих опытов известен вид зависимости , тогда, опреде-
лив параметры этой функции по данным эксперимента на конечном интервале,
мы сможем доопределить саму функцию на бесконечном интервале.
()
tP
()
tP
Для высоконадежных элементов за разумное время не удается построить
оценку функции на требуемом интервале, поэтому применяются либо специ-
альные методы испытаний, либо на основании изучения причин возникновения
отказов выбирается теоретический вид функции
()
tP
(
)
tP и ее параметры оцениваются
по результатам эксперимента. Оценка параметров функции надежности по ре-
зультатам опытов представляет собой самостоятельную задачу, ознакомиться с
которой можно в [1].
Кроме функций и
()
tP
(
)
tQ
(рис. 2.2), в качестве характеристики надежности
часто используется функция
(
)
tq
– плотность вероятности отказа (рис. 2.3):
() () ()
tP
dt
d
tQ
dt
d
tq −== ,
() ( )
∫
=
t
dqtQ
0
ξξ
.
Зная функцию или
()
tQ
(
)
tq
, можно найти вероятность отказа на любом ин-
тервале времени:
{}()()(
∫
=−=<<
2
1
ξξτ
1221
t
t
dqtQtQttP
)
.
Непосредственное дифференцирование оценок
(
)
tP и является непригод-
ным способом для определения оценки
()
tQ
(
)
tq
. Для оценивания функции
(
)
tq
ис-
пользуется гистограмма.
0
t
1
Рис. 2.2. Вероятность отказа
Q(t)
0
t
Рис. 2.3. Плотность вероятности отказа
q(t)
12

В связи с большим объемом испытаний, необходимых для определения пол-
ных характеристик надежности
(
)
tP
(
)
tQ
(
)
tq
, или , во многих случаях предпочи-
тают определять числовые характеристики (моменты) случайной величины τ
(времени жизни элемента).
Важнейшим из них является среднее время безотказной работы (СВБР) или
среднее время жизни элемента, определяемое как математическое ожидание слу-
чайной величины τ:
[]
()
∫
∞
=τ=
0
0
dtttqMT
. (2.3)
Возьмем этот интеграл по частям:
() () () () ()
∫∫∫∫
∞
∞
∞
∞
∞
+−=−=−==
0
0
000
0
dttPttPttdPdttP
dt
d
tdtttqT
. (2.4)
t
1
Предположим, что при
()
tP убывает быстрее, чем
∞
→
t
, что выполняется
для всех употребительных законов распределения функций надежности. Тогда
()
∫
∞
=
0
0
dttPT
. (2.5)
Из этой формулы видно, что среднее время безотказной работы численно рав-
но площади, ограниченной функцией надежности
(
)
tP и осями координат.
Среднее время жизни может быть найдено и непосредственно по результа-
там испытаний. Для этого необходимо
N элементов испытывать до отказа послед-
него из них. Пусть – времена жизни этих элементов. Известно [1], что
для определения математического ожидания целесообразно использовать оценку
вида
0
T
N
τ..., , τ,τ
21
N
T
N
i
i
∑
=
=
1
*
0
τ
, (2.6)
[
]
00
TTM
*
=
которая удовлетворяет свойствам несмещенности, ибо
, и состоятель-
ности, ибо
{
}
0
*
00
→>−
∞→
ε
TTP
N
для любого 0>
ε
. Следовательно, при большом
N имеет место приближенное равенство .
00
TT
*
=
Практически испытания до последнего отказа провести не удается, ибо время
испытаний всегда ограничено. Пусть за время испытаний
t при испытании N
элементов произошло
n отказов в моменты . Используем оценку вида
n
τ..., , τ,τ
21
()
NtnNT
n
i
i
~
1
⎥
⎦
⎤
⎢
⎣
⎡
−+τ=
∑
=
. (2.7)
13
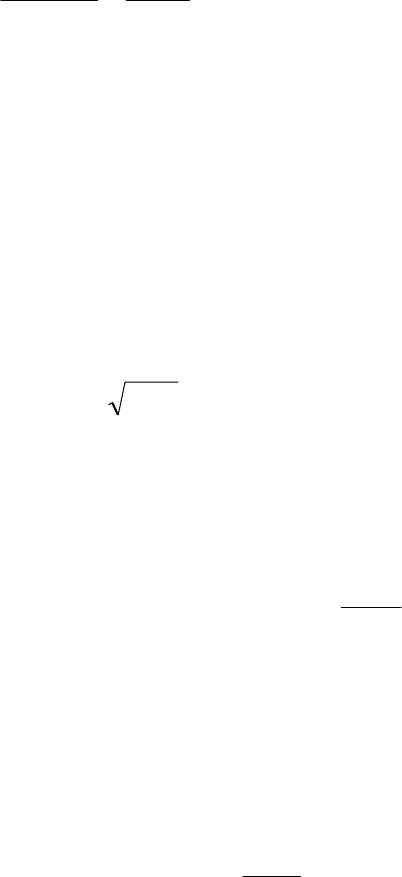
()
NN
tnN
N
ni
i
∑
+=
<
−
1
τ
*
~
T
T
<
Поскольку
, то и, следовательно, оценивает среднее время
жизни
снизу. Естественно, пользоваться такой оценкой целесообразно, если n
близко к N.
0
T
Среднее время безотказной работы является одной из наиболее наглядных ха-
рактеристик надежности. Однако этой характеристике свойственны обычные не-
достатки среднего значения, и для расширения знаний о случайном времени жиз-
ни элемента целесообразно ввести в рассмотрение моменты высших порядков,
например, дисперсию времени жизни:
[]
()
[]
[
]
()
2
0
0
22
0
2
2
0
τττ TdttqtTMTMD
∫
∞
−=−=−=
. (2.8)
[]
τ][τσ D=
Величина дает среднеквадратическое отклонение случайного
времени жизни τ от своего среднего значения .
0
T
Дисперсию времени безотказной работы можно оценить и по результатам
опыта. Используя прежние обозначения, запишем несмещенную и состоятельную
оценку дисперсии в виде
[] []
(
)
∑
=
−
−
=≈
N
i
i
T
N
DD
1
2
**
τ
1
1
ττ
. (2.9)
Укажем, в заключении, способ экспериментальной оценки плотности вероят-
ности отказа . Для этого интервал наблюдения t разбиваем на некоторые ма-
лые интервалы Δt и регистрируем число отказов n
()
tq
k
, попавшее в каждый интер-
вал. Эмпирическая функция плотности вероятности (гистограмма) выражается
формулой
()
tN
n
tq
k
N
Δ
=
при
(
)
tkttk
Δ
<
<
Δ
−
1 . (2.10)
()
(
)
tqtq
N
≈
При большом объеме испытаний и достаточно малых Δt оценка
.
Отметим, что плотность вероятности отказов, согласно формуле (2.10), можно
интерпретировать как частоту отказов, приходящихся на один элемент, в единицу
времени. Частота отказов является наряду с функцией надежности наиболее пол-
ной характеристикой элемента, работающего до полного отказа. Среднее время
безотказной работы и другие характеристики легко вычислить, если известна час-
тота отказа. Соответствующие рекомендации по выбору числа интервалов и объ-
ему выборки можно найти в [6].
Перейдем теперь к рассмотрению важной и очень популярной характеристики
надежности, которую чаще всего называют функцией интенсивности (ФИ) отказа.
Решим следующую задачу: пусть элемент безотказно работает на интервале
[
]
t ,0.
Какова вероятность того, что он не откажет на интервале
t
t
t
Δ+ ,
? Обозначим эту
14
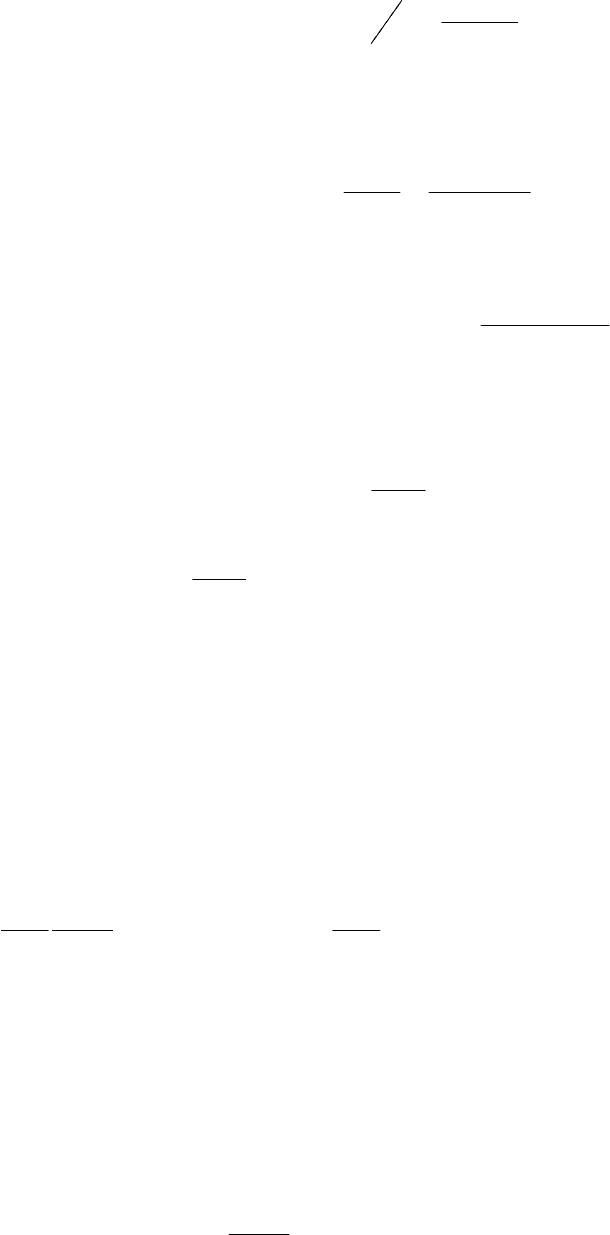
вероятность через . Пусть А – событие, обозначающее безотказную ра-
боту элемента на участке , а B – событие, означающее безотказную работу на
. Тогда искомая вероятность есть условная вероятность:
(
tttP Δ+ ,
)
]
]
[
t ,0
[
ttt Δ+ ,
()
{
}
{
}
{}
AP
ABP
A
B
PtttP ==Δ+ ,
. (2.11)
[]
[
]
1
,0 ,0 ttt
=
Δ
+
Но событие AB означает безотказную работу на интервале
,
поэтому
()
(
)
()
(
)
()
tP
ttP
tP
tP
tttP
Δ
+
==Δ+
1
,
,
t
t
Δ+
а вероятность отказа на
:
()()
(
)(
()
)
tP
tPtP
tttPtttQ
1
,1 ,
−
=Δ+−=Δ+
. (2.12)
Устремляя Δt к нулю, с точностью до бесконечно малой высшего порядка по-
лучаем
()
(
)
()
(
tt
tP
tP
tttQ ΔΟ+Δ
)
′
−=Δ+ ,
. (2.13)
()
()
()
t
tP
tP
λ=
′
−
(
)
tλ
Введем обозначение
и назовем функцией интенсивности от-
каза. Из формулы (2.13) видно, что
(
)
(
)
tttttQ
Δ
≈
Δ
+
λ ,
, (2.14)
а величина является локальной характеристикой надежности изделия и озна-
чает плотность вероятности того, что элемент, исправно работавший на интервале
, откажет в последующий малый (бесконечно малый) промежуток Δt.
()
tλ
[
t ,0
]
Легко установить связь между функцией интенсивности отказа и функцией
надежности. Действительно,
()
()
(
)
dt
tdP
tP
t
1
λ −=
()
()
()
tdP
tP
dtt
1
λ −=
(
)
10
=
P, откуда или, интегрируя с учетом ,
() ()
tPdtt lnλ
t
0
−=
∫
, получаем
() ()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
∫
t
0
λexp dtttP . (2.15)
Отсюда для частоты отказов
()
(
)
() ()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=−=
∫
t
0
λexpλ dttt
dt
tdP
tq
. (2.16)
15
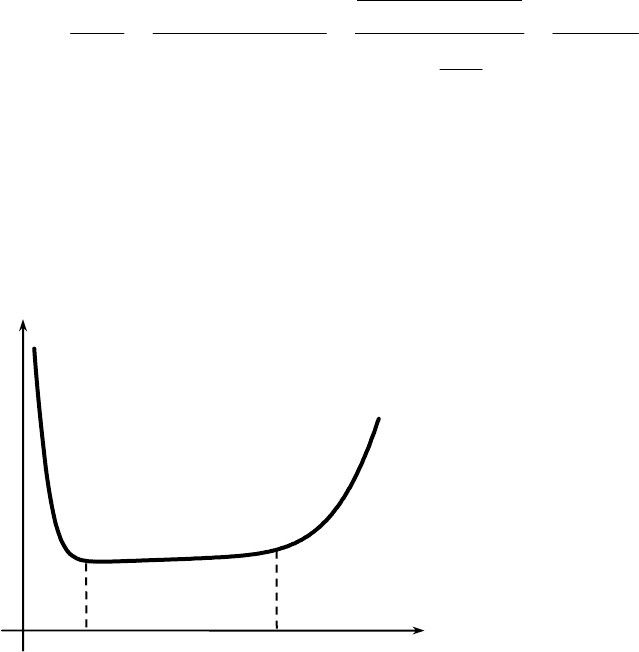
Из уравнения (2.15) следует, что вероятность безотказной работы на интервале
находится как
[
21
, tt
]
() ()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
∫
2
1
λexp ,
21
t
t
dttttP
. (2.17)
Функцию интенсивности отказов можно определить по результатам экспери-
мента следующим образом:
()
()
()
() ( )
()
(
)
(
)
()
()
()
t
tnt
n
N
tn
t
N
ttntn
tPt
ttPtP
tP
tP
t
*
λλ =
⋅Δ
Δ
=
⋅Δ
Δ
+
−
≈
⋅Δ
Δ+−
≈
′
−=
, (2.18)
[
]
ttt
Δ
+
,,
где – число отказов на участке nΔ
а
(
)
tn – число элементов, не отка-
завших к моменту t. Если Δt достаточно мало,
(
)
t
*
λ
n
Δ
при этом велико, то мо-
жет быть принята в качестве оценки функции интенсивности.
Типичная зависимость функции интенсивности имеет характерный вид, пока-
занный на рис. 2.4.
0
t
λ(t)
I II III
Рис. 2.4. Функция
интенсивности:
I – участок приработки;
II – участок нормальной
эксплуатации;
III – старение элемента
(
)
tλ
Физически такой вид зависимости
объяснить просто. На участке I проис-
ходит основное количество отказов, связанное с приработкой изделий и выявле-
нием скрытых отказов. Это участок приработки (“детства” элемента).
На участке II, называемом участком нормальной эксплуатации (“зрелость”
элемента), интенсивность отказов невелика и мало изменяется, но, вообще говоря,
возрастает. Участок III характеризует период старения (“старость” элемента).
Здесь интенсивность отказов снова резко возрастает, что объясняется необрати-
мыми физико-химическими процессами в элементе.
Естественно, что эта кривая (см. рис. 2.4) не является универсальной. Напри-
мер, хорошо поставленный контроль приводит к сильному сокращению или даже
отсутствию периода приработки. Есть сведения, что для некоторых элементов
(например, для интегральных схем) функция интенсивности на участке нормаль-
ной работы убывающая.
16
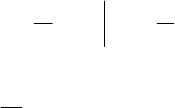
Поскольку для большинства систем эксплуатация начинается после предвари-
тельной тренировки, настройки и регулировки, то можно сказать, что наиболее
интересным для изучения является участок II, так как работа на участке III обыч-
но не допускается, и элемент заменяется ранее, чем он начинает заметно стареть.
2.2. Типовые законы надежности
2.2.1. Экспоненциальный закон
Зачастую, идеализируя реальную картину функции интенсивности, полагают,
что на участке нормальной эксплуатации
(
)
constλ
=
λ
=
t . (2.19)
Как следует при этом из формулы (2.15):
()
t
edttP
λ−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
∫
t
0
λexp , (2.20)
()
t
etQ
λ
−
−=1
(
)
t
etq
λ
−
= λ
, а . (2.21)
Тогда среднее время жизни определяется как
λ
11
0
0
0
=
λ
−==
∞
λ−
∞
λ−
∫
tt
ee dtT
,
()
0
T
t
etP
−
=
поэтому
. (2.22)
Можно сказать, что – это время, за которое вероятность безотказной работы
уменьшается в
e раз.
0
T
Дисперсия и среднеквадратическое отклонение времени жизни:
[]
∫
∞
λ−
=−λ=τ
0
2
0
2
0
2
TTdttD
t
e
[
]
0
T
=
τ
σ
, . (2.23)
Таким образом, при экспоненциальном законе надежности среднеквадратиче-
ское время безотказной работы равно его математическому ожиданию. Это свой-
ство экспоненциального закона позволяет считать, что в данном случае среднее
время безотказной работы является достаточно полной характеристикой надежно-
сти. Кроме того, это свойство на практике может быть использовано для проверки
гипотезы о существовании экспоненциального закона надежности. Если стати-
стическое математическое ожидание и среднеквадратическое отклонение близки
по величине, это может служить выводом о правдоподобности принятой гипоте-
зы.
Для реального элемента не является действительным средним временем
жизни и по той причине, что вне участка нормальной эксплуатации функция ин-
0
T
17
тенсивности изменяется. Поэтому более корректно сказать, что для экспоненци-
ального закона – это среднее время работы некоторого гипотетического эле-
мента, функция интенсивности отказа которого постоянна на бесконечном интер-
вале времени, а на рассматриваемом участке совпадает с интенсивностью отказа
изучаемого элемента.
0
T
Часто интересующее нас время значительно меньше среднего времени работы
, тогда можно воспользоваться более простыми приближенными формула-
ми, которые дают нижнюю оценку соответствующих вероятностей:
0
Tt <<
()
0
1
T
t
tP −≈
()
0
T
t
tQ ≈
,
. (2.24)
Популярность экспоненциального закона в теории надежности объясняется
тем, что он часто имеет физическое обоснование и прост для теоретических ис-
следований. Основное свойство элемента с экспоненциальным законом надежно-
сти заключается в том, что вероятность безотказной работы на интервале
[
]
ttt
Δ
+
,
не зависит от времени предшествующей работы элемента t, а зависит только от
длины интервала Δt. Т. е., если известно, что в данный момент элемент исправен,
то будущее его поведение не зависит от прошлого. Согласно (2.11) имеем
()
(
)
()
(
)
t
t
tt
e
e
e
tP
ttP
tttP
Δλ−
λ−
Δ
+
λ
−
==
Δ+
=Δ+ ,
.
Это свойство является характеристическим, т. е., если оно выполняется для
некоторого закона , то этот закон обязательно является экспоненциальным.
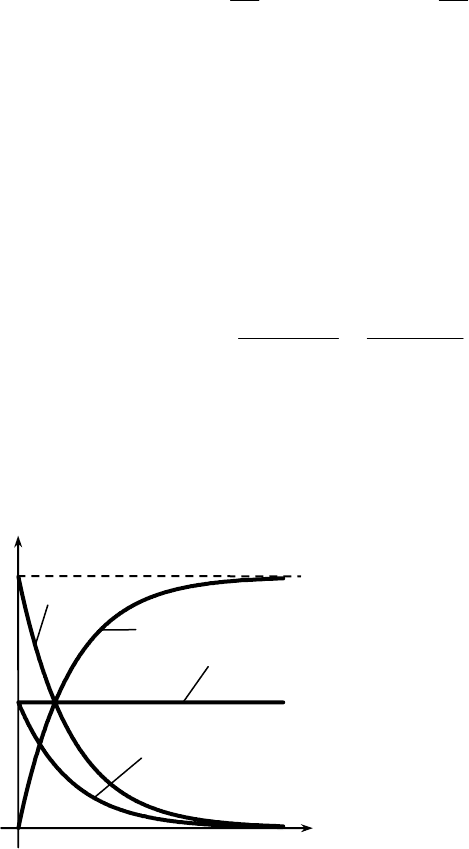
Графические зависимости, отражающие основные характеристики экспоненци-
ального закона, приведены на рис. 2.5.
()
tP
1
0
t
λ
P(t)
Q(t)
λ(t)
Рис. 2.5. Характеристики
экспоненциального
закона надежности
q(t)
Экспоненциальный закон распределения является типичным для радиоэлек-
тронных компонентов, например, резисторов, конденсаторов и т. п. Но часто этот
закон применяется некритически и единственным оправданием в его пользу слу-
жит то, что с этим законом проще решать задачу, а без него она в общем случае
неразрешима. По-видимому, применимость экспоненциального закона зависти, в
основном, от характера отказов элемента. Внезапные отказы, носящие случайный
характер (например, пробой конденсаторов, обрыв сопротивлений и т. п.), обычно
18

довольно широко описываются экспоненциальным законом. Отказы, возникаю-
щие в результате износа и необратимых физико-химических изменений парамет-
ров, не подчиняются экспоненциальному закону. Эти отказы, носящие название
постепенных (параметрических) во многих случаях хорошо описываются сле-
дующими законами.
2.2.2. Нормальный закон
Рассмотрим одну достаточно общую модель, которая приводит к нормальному
закону надежности. Пусть надежность элемента определяется некоторым пара-
метром α
0
, например, величиной сопротивления, коэффициентом усиления и т. п.
Допустим, что начальное значение α
0
– есть случайная величина, вызванная про-
изводственным разбросом. В силу большого количества причин, вызвавших тех-
нологический разброс параметра, можно предположить, что закон распределения
случайной величины α
0
– нормальный.
Во время работы элемента параметр α
0
меняется некоторым образом (напри-
мер, от нагрева), причем можно указать эту зависимость:
(
)
0
α ,α tf
=
.
τ
=
t
определяется из равенства
Момент отказа элемента
(
)
τ,αα
01
f
=
,
где α
1
– критическое (предельное) значение параметра α
0
. Предполагая для про-
стоты функцию f монотонной (практически это часто имеет место), получаем
(
)
10
α ,ατ
ϕ
=
,
где φ – функция, обратная f по аргументу t. Раскладывая эту функцию в ряд
Тейлора в точке и пренебрегая членами второго порядка малости, получа-
ем
[
0
αM
]
(
)
(
)
(
)
0000
αααα 011
α α ,α ,τ mmm
−
ϕ
′
+
ϕ= .
Отсюда видно, что если α
0
имеет нормальный закон распределения, то и время
жизни τ, как линейная функция от α
0
, также имеет нормальное распределение.
Поскольку время работы аппаратуры не может быть меньше нуля, то в теории
надежности имеет смысл рассматривать лишь усеченный нормальный закон рас-
пределения, плотность вероятности отказов для которого определяется для поло-
жительных значений аргумента:
()
()
⎪
⎩
⎪
⎨
⎧
<
≥
=
σ
−
−
0 ,0
0 ,
2
2
1
2
t
tCe
tq
Tt
, (2.25)
()
∫
∞
=
0
1dttq
где постоянная С определяется из условия нормировки
, откуда
19
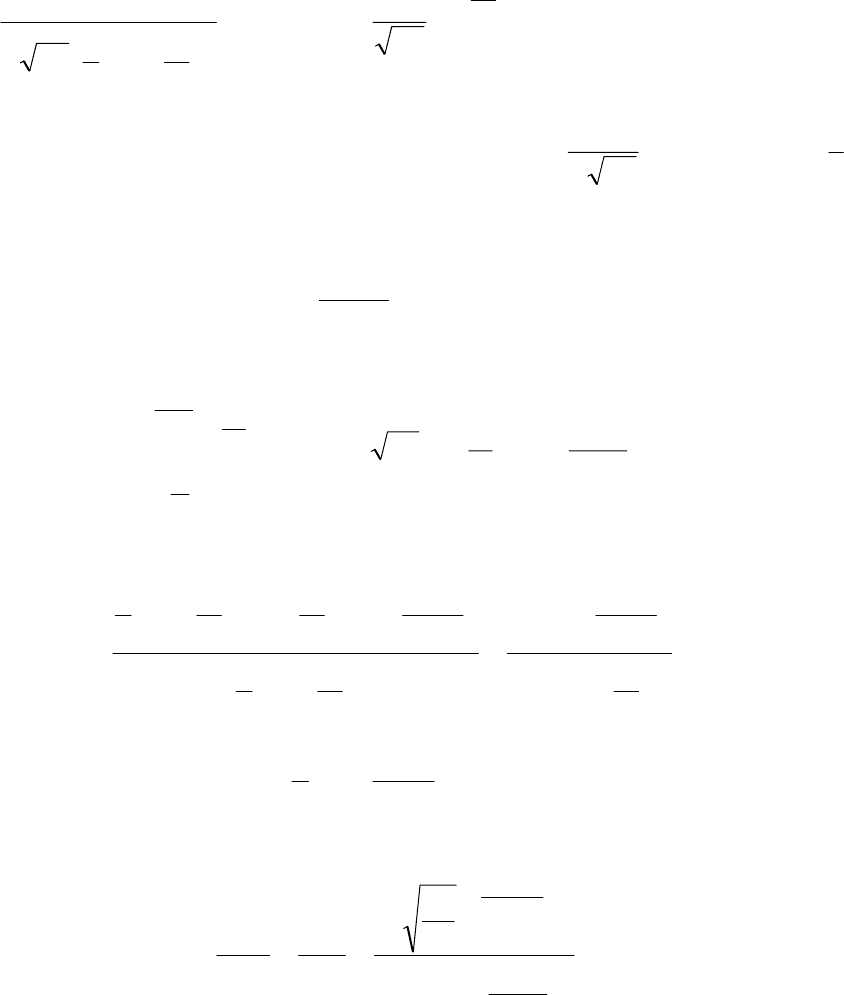
()
∫
−
π
=
x
x
dxex
0
2
2
2
1
Ф
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
+πσ
=
1
Ф
2
1
2
1
T
C
(
)(
xx ФФ −=−
)
.
,
, где
1
3
1
T=σ
πσ
≈
2
1
C
Обычно для реальных элементов σ << T
(уже для
1
и
Ф(3)=0,4986).
Функция надежности для нормального закона
() ()
()
=−=−=
∫∫
σ
−
−
t
T
t
deCdttqtP
0
2
τ
0
τ11
2
2
1
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
+
⎟
⎠
⎞
⎜
⎝
⎛
σ
−=−=
∫
−
−
−
11
σ
σ
2
ФФ2πσ1σ1
1
1
2
TtT
CdxeC
Tt
T
x
.
Подставив значение С, получим
()
⎟
⎠
⎞
⎜
⎝
⎛
σ
+
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
σ
+
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
−
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
⎟
⎠
⎞
⎜
⎝
⎛
σ
+
=
1
1
1
111
Ф21
Ф21
Ф
2
1
ФФФ
2
1
T
Tt
T
TtTT
tP
. (2.26)
()
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
−=
1
Ф
2
1
Tt
tP
(
)
1 0
=
= tPt
При σ << T
1
получаем, что . В частности, при .
Функция интенсивности отказов
()
()
()
()
()
(
)
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
σ
−
−
==
′
−=
σ
−
−
1
2
τ
Ф21σ
π2
1
λ
2
2
1
Tt
e
tP
tq
tP
tP
t
T
. (2.27)
0=
t
и σ << T
В частности, при
1
получаем, что λ(0) ≈ 0. Физически это условие
означает, что элемент, подверженный старению, практически не имеет скрытых
отказов.
Графические зависимости, отражающие основные характеристики нормально-
го закона, показаны на рис. 2.6.
Из рис. 2.6 видно, что интенсивность отказов вначале весьма мала, но с тече-
нием времени сильно растет, вероятность безотказной работы быстро уменьшает-
ся. Следовательно, можно сделать вывод, что из элементов, имеющих нормаль-
ный закон распределения надежности, целесообразно строить системы, предна-
значенные для нормального времени работы.
20
