Сборник задач по дисциплине Системный анализ

11

VII

∑

=

γ=

n

1j

jj

xZ

max

⎪

⎩

⎪

⎨

⎧

+=≤

=≥

==

∑

;n,1nj0x

;n,1j0x

;m,1ibxa

1j

i

j

jij

∑

=

γ=

n

1j

jj

xZ

min

⎪

⎩

⎪

⎨

⎧

=≥

+==

<=≤

∑

;n,1j0x

;m,1mjbxa

mm;m,1ibxa

j

1i

j

jij

11i

j

jij

VIII

IX

∑

=

γ=

n

1j

jj

xZ

min

⎪

⎩

⎪

⎨

⎧

=≥

==

<+=≥

<=≤

∑

n,1j0x

;m,mibxa

mm;m,1mibxa

mm;m,1ibxa

j

2i

j

jij

221i

j

jij

211i

j

jij

∑

=

γ=

n

1j

jj

xZ

min

⎪

⎩

⎪

⎨

⎧

+=≤

=≥

<+==

<+=≤

<=≥

∑

n,1nj0x

;n,1j0x

nn;m,1mibxa

mm;m,1mibxa

mm;m,1ibxa

1j

12i

j

jij

1221i

j

jij

211i

j

jij

X

Задание №11

№

вар.

1.Составить двойственную задачу к данной и проверить их взаимную

двойственность, считая все x

j

≥ 0,

n,1j =

;

2.решить данную задачу симплекс-методом и найти решение двойственной

из последней таблицы;

3.Найти решение двойственной по формуле

1

ББопт

АСY

−

=

;

4.Найти решение двойственной по второй теореме двойственности.

5.Найти, как изменится Z

опт

при увеличении b

1

на 10%;

6.решить данную двойственным симплекс-методом.

№

вар.

I

Z = 9x

1

+ 8x

2

+ 4x

3

min

⎩

⎨

⎧

≥−+

≥++−

2xxx3

1xxx2

321

Z = 6x

1

+ 9x

2

+ 3x

3

min

⎩

⎨

⎧

−≥−+

≥++−

2xxx3

1xxx2

321

II

III

Z = 9x

1

+ 8x

2

+ 4x

3

min

⎩

⎨

⎧

≥−−

≥++−

1xxx3

2xx2x

321

Z = 4x

1

+ 2x

2

+ 3x

3

min

⎩

⎨

⎧

≥−+

≥++−

2xxx3

1xxx2

321

IV

V

Z = 6x

1

+ 9x

2

+ 3x

3

min

⎩

⎨

⎧

≥−+

≥++−

2xxx3

1xxx2

321

Z = x

1

+ 4x

2

+ 5x

3

min

⎩

⎨

⎧

≥−+

≥++−

2xxx3

1xxx2

321

VI

VII

Z = 6x

1

+ 9x

2

+ 3x

3

min

⎩

⎨

⎧

≥−−

≥++−

1xxx3

2xx2x

321

Z = x

1

+ 4x

2

+ 5x

3

min

⎩

⎨

⎧

≥−−

≥++−

1xxx3

2xx2x

321

VIII

IX

Z = 6x

1

+ 9x

2

– 3x

3

min

⎩

⎨

⎧

−≥−+

≥++−

1xxx3

2xxx2

321

Z = x

1

+ 4x

2

+ 5x

3

min

⎩

⎨

⎧

≥−+

≥++−

1xxx3

1xx2x

321

X

12

1 2 3 4 5 6 7 8 9 10 11

Ответ:

"Z

min

"

17/7 18/5 29/5 32/5 69/5 87/5 92/5 3 9 13 Не знаю

Задание №12

№

вар.

А. Определить, является ли указанный вектор

0

X

оптимальным решением

данной задачи;

Б. Решив двойственную к данной графически, найти решение исходной.

№

вар.

I

Z = x

1

+ 8x

2

+ 10x

3

max

⎩

⎨

⎧

=+−

=++

0x2xx

2x4xx

321

x

1,2,3

≥ 0;

0

X

=(1,0,0)

Z = x

1

+ 4x

2

+ x

3

max

⎩

⎨

⎧

=−+

=++

0xxx

7x3x11x4

321

x

1,2,3

≥ 0;

0

X

=(0,1/2,1/2)

II

III

Z = x

1

+ x

2

+ x

3

max

⎩

⎨

⎧

=+−

=−+

1x6xx

1x12x17x

321

x

1,2,3

≥ 0;

0

X =(1,0,0)

Z = x

1

+ x

2

+ x

3

min

⎩

⎨

⎧

=+−

=−+

3xx2x

0x3xx

321

x

1,2,3

≥ 0;

0

X =(1,0,1)

IV

V

Z = -4x

1

- 3x

2

- 2x

3

- 5x

4

max

⎩

⎨

⎧

=−+−

=+++

0xxxx

4xxxx

4321

x

1,2,3,4

≥ 0;

0

X

=(0,2,2,0)

Z = x

1

- 3x

2

+ x

3

max

⎩

⎨

⎧

=−+

3x6x5x

2x5x4x

321

x

2,3

≥ 0;

0

X

=(2,1,0)

VI

VII

Z = 2x

1

+ 3x

2

- 7x

3

+ 14x

4

max

⎩

⎨

⎧

−≤+−+

≤+++

2x7x4x2x

2xxxx

4321

x

1,2,3,4

≥ 0;

0

X

=(0,1,1,0)

Z = x

1

+ x

2

- 2x

3

- 3x

4

max

⎩

⎨

⎧

=−+−

9x6x11x5x

1x2x3xx

4321

x

3,4

≥ 0;

0

X

=(-1,-2,0,0)

VIII

IX

Z = x

1

+ x

2

- 4x

3

max

⎩

⎨

⎧

=+−

=−+

3xx2x

0x3xx

321

x

1,2,3

≥ 0;

0

X =(1,0,1)

Z = x

1

+ x

2

+x

3

min

⎩

⎨

⎧

=−−

=++

0xxx

1x4x3x2

321

x

1,2,3

≥ 0;

0

X =(1,1,0)

X

Ответ для "А": 1. Да; 2. Нет; 3. Не знаю.

Ответ для "Б" (реше-

ние двойственной):

1.Y

0

= (-5/2,1/2);

2. Y

0

= (-1/3,5/3);

3. Y

0

= (0,1);

4. Y

0

= (5/18,13/18);

5. Y

0

= (2/7,1/7);

6. Y

0

= (2/5,-1/5);

7. Y

0

= (5/4,-1/4);

8. Y

0

= (3/2,-1/2);

9. Y

0

= (9/2,-7/2);

10. Y

0

= (13,-11);

11. Не знаю.

Задание №13

№

вар.

Построить двойственную задачу к данной. Решив одну из них, найти оп-

тимальное решение другой любым известным способом. (все x

j

≥ 0,

n,1j =

)

№

вар.

I

Z = 4x

1

+ 3x

2

+ 5x

3

max

⎪

⎩

⎪

⎨

⎧

≥++

≥+−

≤++

12xx2x3

10x3xx2

8xxx

321

Z = 2x

1

+ 3x

2

+ 4x

3

max

⎪

⎩

⎪

⎨

⎧

≥++

≥+−

≤++

15xx2x4

10x3xx2

7xx2x

321

II

13

III

Z = -2x

1

+ 3x

2

+ x

3

max

⎪

⎩

⎪

⎨

⎧

≤++−

≤+−−

≥++

7x3x3x2

4x2xx2

6xxx

321

Z = x

1

+ 3x

2

- x

3

+2x

4

min

⎪

⎩

⎪

⎨

⎧

≤+−

≥−+−

=+−+

7x2xx

3xxxx3

4xx2x2x

431

4321

IV

V

Z = x

1

+ 2x

2

+ x

3

- 3x

4

max

⎪

⎩

⎪

⎨

⎧

≥+

=+

≤++−

10xx4

11xx2

8xx2x

21

31

421

Z = -3x

1

+ x

2

- 3x

3

- 2x

4

max

⎩

⎨

⎧

≤+−+

−≤+++−

2x3xxx2

1x3x3xx5

4321

VI

VII

Z = 3x

1

- 2x

2

- x

3

min

⎪

⎩

⎪

⎨

⎧

=++

≤++

≥+−

4xxx

6xx2x3

2xxx2

321

Z = 5x

1

+ 4x

2

+ 6x

3

max

⎪

⎩

⎪

⎨

⎧

≥++

≥+−

≤++

11x2xx3

9x3xx2

6xxx

321

VIII

IX

Z = 2x

1

+ 3x

2

+ x

3

+x

4

min

⎪

⎩

⎪

⎨

⎧

≤−

≥−+−

=+−+

4xx

3xxx2x

2xx2xx2

31

4321

Z = 4x

1

+ 3x

2

+4x

3

+ x

4

-x

5

max

⎪

⎩

⎪

⎨

⎧

=+−

=−++

8x2xx

14x2x2xx2

8xxx2x

432

5321

4321

X

Ответ для "Z

опт

": 1. 95;

2. 40;

3. 38;

4. 68/3;

5. 21;

6. 7;

7. 5;

8. 4;

9. -1/7;

10. -5;

11. Не знаю.

Задания №14, №15, №16 – транспортные задачи.

Задание №14

№

вар.

Решить методом потенциалов транспортную задачу, заданную матрицами:

А - запасов; В - потребностей; С - тарифов.

№

вар.

I

()

85608075B

50

150

100

A

120103

6521

5376

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

15402020B

40

30

25

A

65410

9875

5341

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

II

III

()

15302520B

30

20

40

A

3962

8743

2154

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

20352530B

20

40

50

A

4123

5132

1423

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

IV

V

()

10352520B

20

40

30

A

6234

1423

4532

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

70503895B

68

70

115

A

1697

5812

9374

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

VI

VII

()

25456030B

40

70

50

A

11928

2695

3174

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

705080120110B

110

170

150

A

871053

16348

951127

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

VIII

14

IX

()

5060304070B

120

110

20

A

23411

54387

67524

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

5030204010B

50

70

30

A

42675

37549

26372

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

X

Ответ для "Z

опт

": 1. 930;

2. 690;

3. 665;

4. 518;

5. 495;

6. 470;

7. 435;

8. 240;

9. 215;

10. 190;

11. Не знаю.

Задание №15

№

вар.

Решить методом потенциалов транспортную задачу, заданную матрицами:

А - запасов; В - потребностей; С - тарифов.

№

вар.

I

()

2516209B

15

25

A

5482

3764

2513

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

30404035B

30

50

40

A

4423

5132

1423

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

II

III

()

606412575B

120

72

112

A

7359

12083

27413

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

10201018B

40

30

28

A

61064

7528

4673

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

IV

V

()

14121618B

38

50

A

94510

7532

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

1210`8B

15

20

A

312

231

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

VI

VII

()

45303540B

40

34

46

A

4953

4611

7234

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

50203040B

50

70

60

A

5248

4932

1542

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

VIII

IX

()

15121816B

22

14

16

20

A

1854

2215

1643

7932

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

()

304520B

36

40

74

A

951

284

637

C

=

⎟

⎠

⎞

⎜

⎝

⎛

=

⎟

⎠

⎞

⎜

⎝

⎛

=

X

Ответ для "Z

опт

": 1. 965;

2. 320;

3. 287;

4. 215;

5. 214;

6. 210;

7. 190;

8. 162;

9. 80;

10. 42;

11. Не знаю.

Задание № 16

№

вар.

Построить математическую модель транспортной задачи и найти ее ре-

шение методом потенциалов.

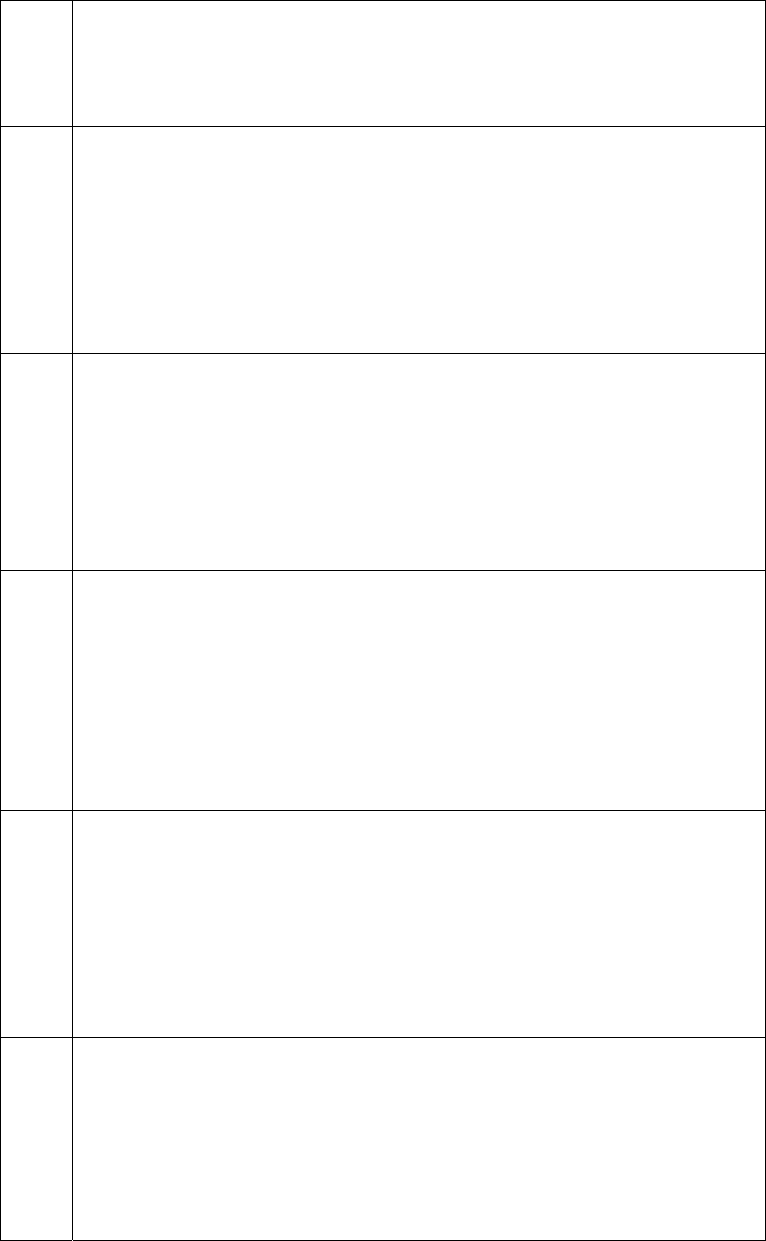
I Составить план перевозок каменного угля с трех шахт в четыре пункта.

Производительность шахт (тыс.т) равна соответственно 100; 150; 50. По-

требности заказчиков равны: 75; 80; 60; 85 тыс. т. Стоимость перевозки

одной тонны угля задается элементами матрицы

15

⎟

⎠

⎞

⎜

⎝

⎛

420103

6521

5376

.

Составить план перевозки, обеспечивающий минимальные транспортные

издержки.

II Три совхоза выделяют соответственно 40; 50; 30 ц молока для ежедневно-

го снабжения четырех пунктов, потребности которых составляют соответ-

ственно 20; 40; 30; центнеров молока. Стоимости перевозок 1 ц молока

задаются матрицей

⎟

⎠

⎞

⎜

⎝

⎛

8,22,48,36

155,42

45,35,23

.

Организовать снабжение так, чтобы потребители были обеспечены моло-

ком, а транспортные расходы были минимальны.

III В четырех хранилищах имеются соответственно 40; 50; 60 и 30 т топлива.

Требуется спланировать перевозки так, чтобы спрос трех потребителей,

составляющий соответственно 60; 80; 40 т, был удовлетворен, а затраты

на транспортировку были минимальны. Стоимость перевозок 1 тонны то-

плива задаются матрицей

⎟

⎠

⎞

⎜

⎝

⎛

365

247

126

534

.

IV С четырех складов, где хранится соответственно 50; 160; 70; 100 т карто-

феля, необходимо вывезти его в пять торговых точек. Объем завоза со-

ставляет соответственно 80; 100; 90; 50; 60 тонн. Стоимости перевозок 1 т

картофеля задаются матрицей

⎟

⎠

⎞

⎜

⎝

⎛

34562

23743

62435

16324

.

Закрепить поставщиков за торговыми точками так, чтобы

общая сумма

затрат на перевозку была минимальной.

V Товары с четырех баз поставляются в четыре магазина. Запасы товара на

базах составляют 40; 60; 40; 80 тысяч единиц. Потребности магазинов

равны (тыс. ед.) 30; 80; 60; 50. Затраты на перевозку 1 тысячи единиц за-

даны матрицей

⎟

⎠

⎞

⎜

⎝

⎛

8,55,21,42,3

1654

2,1235,4

.

Спланировать перевозки так, чтобы полностью удовлетворить

потребно-

сти магазинов, а затраты на перевозку свести к минимуму.

VI Продукцию трех заводов (тысячи единиц) 40; 50; 30 соответственно необ-

ходимо доставить потребителям, спрос которых составляет 20; 50; 45; 30

тысяч единиц. Известна матрица транспортных расходов:

⎟

⎠

⎞

⎜

⎝

⎛

8,35,67,53,4

3,65,34,70,3

41,53,45,6

.

Составить план перевозок так, чтобы суммарные транспортные расходы

были минимальны

.

16

VII Найти оптимальный план перевозок по данным задачи VI варианта при

дополнительном условии обязательного полного удовлетворения спроса

второго потребителя b

2

= 50 тыс.ед.

VIII Собранный урожай зерна в четырех совхозах должен быть перевезен на

три элеватора, мощности которых составляют соответственно 90; 70; 50

тысяч тонн. Составить план перевозки зерна, минимизирующий транс-

портные расходы, если урожай по совхозам составил (тыс.т): 50; 60; 70;

40. Известна матрица транспортных расходов:

⎟

⎠

⎞

⎜

⎝

⎛

5,114,141,18

3,156,187,13

7,235,123,27

4,170,225,10

.

IX Заводы №1, 2, 3 производят однородную продукцию в количестве соот-

ветственно 490; 450 и 470 единиц. Продукция отправляется в три пункта,

потребности которых равны соответственно 300; 340 и 360 единицам. Из-

вестна матрица транспортных расходов:

⎟

⎠

⎞

⎜

⎝

⎛

124

543

157

.

Организовать перевозки так, чтобы суммарная стоимость транспортных

расходов была минимальной, при условии, что коммуникации между за-

водом №2 и первым пунктом не позволяют пропускать в рассматривае-

мый период более 200 единиц продукции.

X Найти оптимальное распределение трех видов механизмов, имеющихся в

количестве 45; 20 и 35, между четырьмя участками работ, потребности

которых составляют соответственно 10; 20; 30; 40 механизмов при сле-

дующей матрице производительности каждого из механизмов на соответ-

ствующем участке работы:

⎟

⎠

⎞

⎜

⎝

⎛

6760

0353

5045

.

Нулевые элементы означают, что данный механизм не может быть ис-

пользован на данном участке работы.

Ответ:

"Z

min

"

1. 2618;

2. 1640;

3. 1020;

4. 805;

5. 565;

6. 560;

7. 528;

8. 460;

9. 451;

10. 296.

Задание №17 – целочисленное линейное программирование.

Задание №17

№

вар.

Решить полностью целочисленную задачу:

1.Методом Гомори.

2.Методом ветвей и границ. Все x

j

≥ 0,

n,1j =

.

№

вар.

I

Z = x

1

+ 2x

2

max

⎩

⎨

⎧

≤+

7x3x

7xx3

21

Z = 7x

1

+ 4x

2

max

⎩

⎨

⎧

≤+

37x3x6

21x2x3

21

22

II

17

III

Z = 110x

1

+ 90x

2

max

⎪

⎩

⎪

⎨

⎧

≤

≤+

5x

8xx2

10x4x3

2

21

Z = x

1

max

⎩

⎨

⎧

=+−

=++

24xx8x3

12xx3x

421

321

IV

V

Z = x

4

- x

5

min

⎪

⎩

⎪

⎨

⎧

=++

=+−

=−+

3xx3x

2xx2x

1x2xx

543

542

541

Z = x

1

- x

2

max

⎩

⎨

⎧

=++

=+−

3xx3x

1xx2x

421

321

VI

VII

Z = 7x

1

+ 3x

2

max

⎩

⎨

⎧

≤+

38x4x8

20x2x5

21

Z = 2x

1

- 2x

2

+ 3x

3

- 3x

4

min

⎪

⎩

⎪

⎨

⎧

=++

=+

=+−

4xxx3

5xx

3xx2x

542

32

421

VIII

IX

Z = 3x

1

+ 4x

2

max

⎩

⎨

⎧

=++

=+−

10xx4x

8xx2x3

421

321

Z = x

1

+ 8x

2

max

⎩

⎨

⎧

≤+−

≤+

9xx4

19xx3

21

X

Ответ: 1. 1;

2. 2;

3. 5;

4. 6;

5. 9;

6. 14;

7. 29;

8. 45;

9. 116;

10. 310;

11. Не знаю.

Задание №18 – задачи нелинейного программирования.

Задание №18

№

вар.

Найти условный экстремум функции Z = f (x

1

,x

2

), если переменные связа-

ны условием ϕ(x

1

,x

2

) = 0.

№

вар.

I

Z = 6 - 4x

1

- 3x

2

;

1xx

2

1

=+

;

Z = x

1

⋅ x

2

;

x

1

+x

2

= 1;

II

III

;1xx

;

3

x

2

x

Z

2

1

21

=+

+=

;1

3

x

2

x

;xxZ

21

2

1

=+

+=

IV

V

;2xx

;xxZ

21

2

1

=+

+=

;4xx

;xxZ

2

1

21

=+

⋅

=

VI

VII

;

4

1

x

1

x

1

;

x

1

x

1

Z

2

1

21

=+

+=

;5xx

;x2xZ

5

2

1

21

=+

+

=

VIII

IX

;4xx

;xxZ

21

2

1

=⋅

+=

;5x3x2

;xxZ

21

=+

⋅

=

X

Ответ:

"Z

min

"

1. -5;

2. -4;

3. -52/2;

4.

613−

;

5. 1;

6. 2;

7. 36/13;

8. 38;

9. Не знаю.

Ответ:

"Z

max

"

1. 25/24;

2.

613

;

3. 1/4;

4.

22

;

5. 1;

6. 4

7. 5;

8. Не знаю.

18

В каждом задании 10 однотипных задач. Для каждого задания

даны варианты ответов. Номер ответа не соответствует номеру зада-

чи. Решив задачу, студент должен найти полученный им результат

среди ответов задания.

Сборник задач по дисциплине Системный анализ

Подождите немного. Документ загружается.