Савельева А.Д., Нарциссова П.В. Кристаллография и минералогия

Подождите немного. Документ загружается.

зом. Возьмем кристалл горного хрусталя, измельчим его, перемешаем. За-

тем отберем несколько крупинок кристалла и для каждой определим хи-

мический состав. Во всех случаях получим идентичный результат - SiO

. В

этом суть химической однородности кристаллов. Вполне очевидно, что

свойство подобной однородности сохраняется до определенных пределов

дисперсности вещества. Если же экспериментатору вдруг удалось полу-

чить в одном случае, к примеру SiO

, а в другом – отдельно кремний и ки-

слород, то это означает, что во втором случае кристалл горного хрусталя

(кварца) был расщеплен на уровне элементарных частиц и о кристалле как

таковом уже говорить не приходится.

Вообще существуют следующие определения однородности строе-

ния тел: однородными называют тела, обладающие одинаковыми свойст-

вами во всех своих точках; однородным может быть названо тело с равно-

мерным распределением слагающих его частиц.

Что же касается кристаллов, то следует придерживаться более стро-

гих определений однородности: однородностью кристалла называется та-

кое распределение его частиц, при котором все они расположены относи-

тельно одной из них так же, как и относительно любой другой; все парал-

лельные равноотстоящие направления в кристалле называются однород-

ными.

Вполне очевидно, что кристаллическая однородность – это специ-

фическое свойство и оно также является следствием решетчатого строения

кристаллов.

Понятие макроскопической однородности означает, что в любых

участках кристаллического вещества все свойства его тождественны.

Вместе с тем следует еще раз подчеркнуть, что само понятие макроско-

пического уровня измерения свойства подразумевает проведение экспе-

римента над такими длинами L, поверхностями S и объемами V кристал-

ла, когда перестают проявляться дискретное атомное строение и микро-

периодичность этого строения, т.е. когда L >> а, S >> а

, V >> а

, где а –

наибольший из периодов решетки кристаллов. Для большинства кристал-

лов а ≈ Ǻ (нм), поэтому практически при всех измерениях макросвойств

образцы имеют такие размеры L, что требование L >> а заведомо выпол-

няется.

Измеряя любое свойство кристалла F – скалярное, векторное или

тензорное – следует иметь в виду, что измерение производится при фик-

сированных термодинамических условиях: давлении Р, температуре Т и

определенных внешних воздействиях. Тогда понятие кристаллической од-

нородности означает независимость любого свойства F при переходе от

измерения в точке х (х

, х

) к любой другой точке х+х' (х

+х

', х

+х

'):

F (х) = F (х + х') (1)

2.5. Анизотропность

Твердые тела делятся на изотропные (равно-свойственные) и

анизотропные (неравно-свойственные). Все кристаллы – анизотроп-

ные тела (исключение – оптические свойства кристаллов кубической

сингонии и некоторые др.).

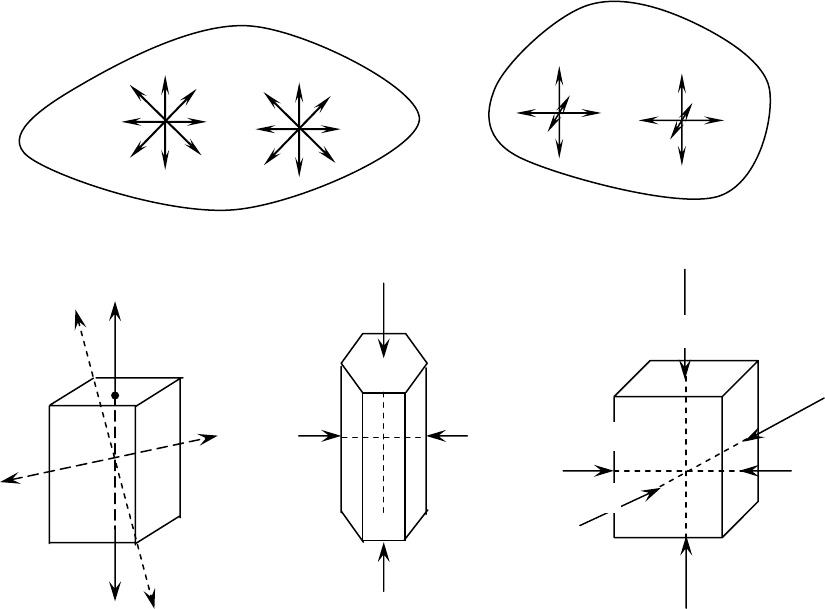
Наглядно различие изотропности тел и анизотропности кри-

сталлов иллюстрирует рис. 10, где а) векторы свойства в изотропном

теле равны во всех направлениях; б) в анизотропном теле величина

вектора свойства изменяется в зависимости от направления; в)

прочность на разрыв (г/мм

) кристалла галита в различных направ-

лениях различна; г) твердость кристалла дистена в направлении с

значительно ниже, чем в направлении б; д) окраска кордиерита в

различных направлениях неодинакова.

Все непараллельные, неравноотстающие направления в кри-

сталле являются анизотропными. В этом легко убедиться, взяв в ру-

ки шариковую модель структуры кристалла галита (поваренной со-

ли).

Анизотропия хорошо проявляется и во внешней форме многих

кристаллов – в их удлиненности или пластинчатости; в механиче-

ских свойствах, например в спайности – способности некоторых

кристаллов легко раскалываться вдоль определенных плоскостей.

Деформационные свойства кристаллов также существенно зависят

от направления.

Таким образом, в соответствии с принципом макроскопической

однородности можно отнести свойства F к произвольной точке. Вы-

брав теперь любое начало координат, анизотропию легко предста-

вить как ориентационную зависимость его от направления n, вдоль

которого определяется свойство:

F (n

) ≠ F (n

) (2)

Рис. 10. Изотропное (а) и анизотропные (б, в, г, д) тела

2.6. Способность самоограняться

Все кристаллы – гранные тела. В процессе своего роста при равно-

весных условиях кристаллы приобретают естественную форму многогран-

ников с плоскими гранями. Такие правильно ограненные поверхности воз-

никают и в процессах, обратных росту, - при растворении или испарении

кристаллов. Естественное самоогранение, очевидно, представляет собой

проявление правильного внутреннего атомного строения кристаллического

вещества.

Если поместить неправильной формы кусочек кристалла в раствор с

Индиговая

Желтая

д)

2150

570

1150

в)

4,5

6,0

г)

б'

в'

г'

ло

а'

б'

в'

Кристалл

а)

б)

Синяя

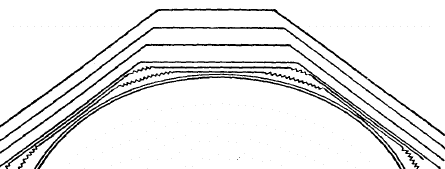
соответствующими условиями, то через некоторое время он обрастет гра-

нями и примет форму правильного многогранника, свойственную кристал-

лам данного вещества. Так, например, вырезанный из кубического кри-

сталла каменной соли (NaCl) шар в насыщенном растворе снова примет

форму куба (рис. 11).

Рис. 11. Схема превращения кристалла с

искусственно приданной шаровой формой

в анизотропную форму

Кристаллы какого-либо вещества чаще всего характеризуются нали-

чием у них граней определенного вида, что нередко позволяет установить

природу минерала по внешнему виду его кристаллов (например кварц

SiO

). В других сравнительно редких случаях внешние формы кристаллов

одного и того же вещества отличаются в зависимости от условий образо-

вания необычайным разнообразием. В частности, у кальцита (CaCO

) из-

вестно более двухсот различных типов граней кристаллов.

2.7. Симметричность

Все кристаллы – симметричные тела. Понятие о симметрии – одно из

наиболее обобщающих фундаментальных понятий физики и естествозна-

ния в целом – пронизывает всю кристаллографию и лежит в ее основе.

Симметрия – это наиболее общая закономерность, присущая строению и

свойствам кристаллического вещества: она, как иногда говорят, является

"свойством свойств кристаллов". Однако симметрия не есть специфическое

свойство, так как присуща множеству тел материального мира (рис. 12).

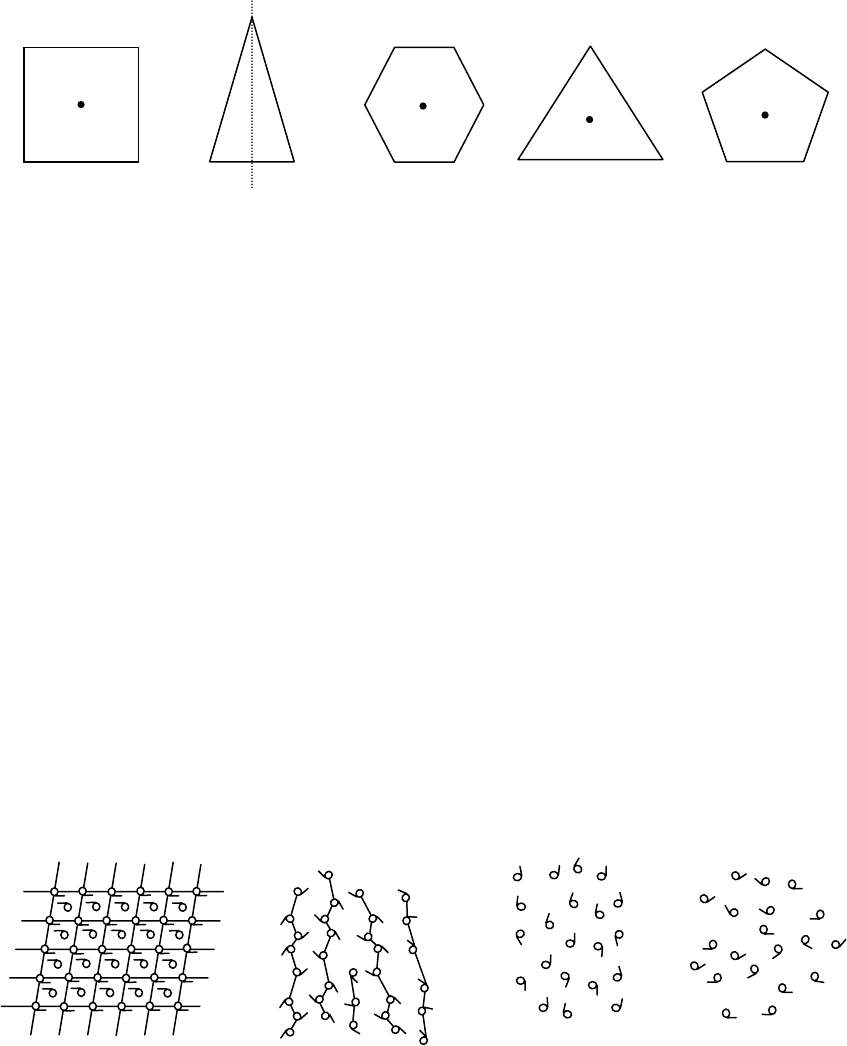
Свойство симметрии следует рассматривать как возможность произве-

сти преобразование системы координат объекта (кристалла) так, что относи-

тельно новой системы он может быть описан точно так же, как и относительно

исходной. Симметричный объект в трехмерном пространстве – это такой объ-

ект, который может быть совмещен с собой поворотами и (или) отражениями.

Рис. 12. Различные симметричные фигуры

Функция F тогда симметрична, если она инвариантна к преобразова-

нию всех или части переменных. Пусть х (х

, х

, …, х

) – аргументы функ-

ции F, а х' (х

, х

, …, х

), …, х

(

)

(х

(

)

, х

(

)

, …, х

(

)

) – преобразование ар-

гумента этой функции. Тогда соотношения:

F (х) = F (х

) = … = F (x

(

)

) (3)

и есть условия симметрии (инвариантности) функции F.

Изучив основные свойства и специфические особенности кристал-

лов, дадим современное определение кристалла. Кристаллами называются

твердые тела, структура которых построена по принципу пространствен-

ной решетки и для которых характерны однородность и анизотропность их

свойств и способность к самопроизвольному образованию правильных

многогранников.

Рис. 13 наглядно иллюстрирует различие между основными типами

конденсированных систем – кристаллами (а), полимерами (б), жидкими

кристаллами (в), аморфными телами (г).

Рис. 13. Мотивы структур основных типов конденсированных систем

а)

б)

г)

в)

Вопросы и задания для самоконтроля

1. Что называется периодом трансляции, трансляцией, узлами ряда?

2. Какие условия необходимо выполнять при выборе элементарной

ячейки?

3. Какая ячейка называется примитивной элементарной ячейкой?

4. Что называется ретикулярной плотностью сетки?

5. Дайте определение пространственной решетки.

6. Что называется элементарной ячейкой?

7. Какая разница между кристаллической структурой и пространствен-

ной решеткой?

8. Чем обусловлена геометрически правильная форма кристаллов?

9. Какому значению внутренней энергии отвечает кристаллическое со-

стояние вещества и почему?

10. Какая специфическая особенность кристаллов подтверждает, что все

кристаллы являются истинно твердыми телами?

11. Какие тела называются однородными?

12. Какие кристаллы называются однородными?

13. Какое тело называется анизотропным?

14. Приведите примеры минералов с резко выраженной анизотропно-

стью.

15. Какое свойство характерно только для кристаллов?

ГЛАВА 3. ЗАКОНЫ КРИСТАЛЛОГРАФИИ

3.1. Закон постоянства углов кристаллов. Формула Вульфа - Брэгга

Когда кристалл растет, частицы выстраиваются в закономерные и

симметричные ряды, сетки, решетки. Грани кристаллических многогран-

ников соответствуют плоскостям, составленным из материальных частиц,

ребра кристалла – линиям пересечения этих плоскостей, т.е. рядам матери-

альных частиц. Центры тяжести частиц могут образовывать плоские сетки

и ряды решетки. Очевидно, любой ряд в структуре соответствует возмож-

ному ребру кристалла, а любая плоскость – возможной грани кристалла.

Кристалл растет так, что частицы вещества из окружающей среды

отлагаются на его гранях. Грани нарастают параллельно самим себе (рис. 14).

Меняются площади граней, их форма, какие-то грани могут вытес-

няться соседними и зарастать, но взаимный наклон граней остается неиз-

менным. Поэтому углы между гранями тоже остаются постоянными.

В этом заключается первый количественный

закон кристаллографии, открытый в 1669 г. Нико-

лаем Стеноном, - закон постоянства углов: во всех

кристаллах данного вещества при одинаковых ус-

ловиях углы между соответствующими гранями

кристаллов постоянны.

Кристаллы разных веществ отличаются друг

от друга по своей внешней форме. У кристаллов

одного и того же вещества облик (габитус) может

оказаться совсем различным, размеры, формы и даже число граней разные,

но углы между соответствующими гранями кристаллов одного вещества

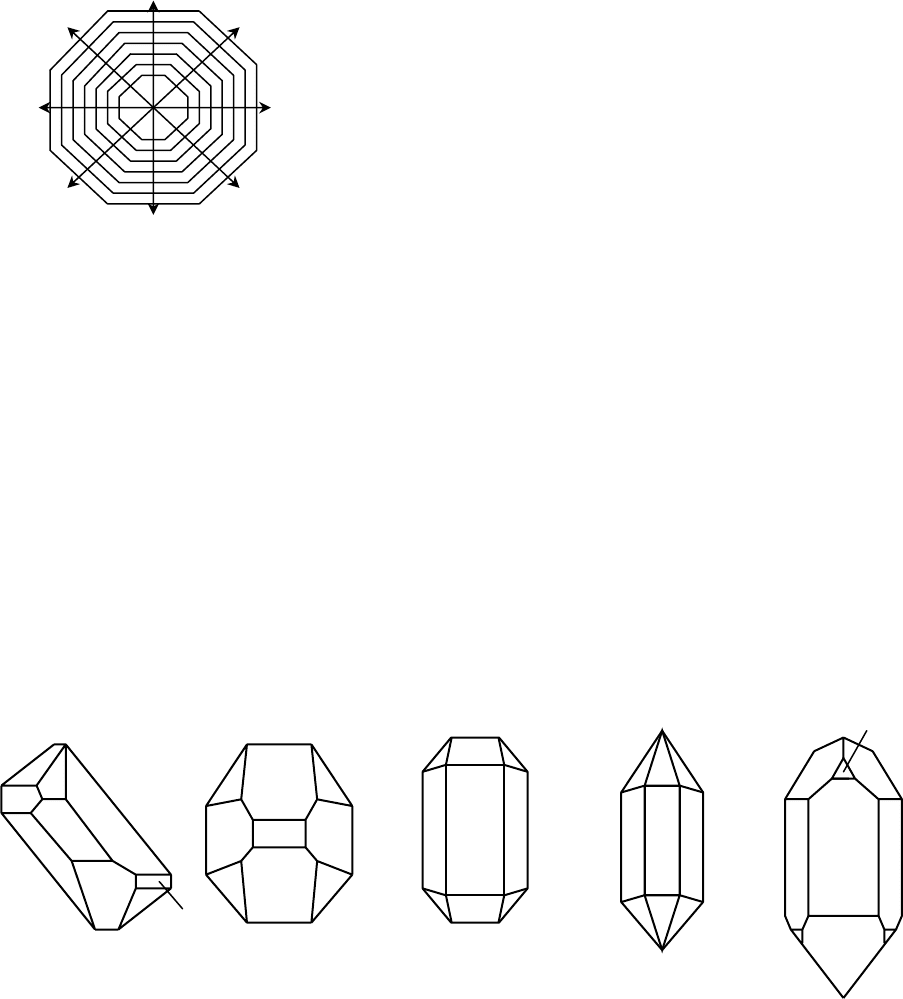
всегда постоянны. Так, например, у различных кристаллов кварца, изобра-

женных на рис. 15, величина углов между гранями а и b, b и c независимо

от формы этих граней всегда сохраняет постоянное значение, поскольку

грани кристалла представляют собой плоские сетки пространственной ре-

шетки кристалла. Так как углы наклона соответственных сеток относи-

тельно друг друга постоянны, то постоянны и углы между гранями кри-

сталла (∠ аb =141°47', ∠ ас =113°08', ∠ bс =120° и т.д.).

Рис. 15. Кристаллы кварца, иллюстрирующие закон постоянства двугранных углов

Закон постоянства углов дает возможность свести все многообразие

форм кристаллических многогранников к совокупности углов между гра-

нями и изобразить их с помощью проекции. Этот закон сыграл огромную

роль в развитии кристаллографии. До открытия дифракции рентгеновских

лучей и разработки рентгеноструктурного анализа кристаллические веще-

ства характеризовали и отличали одно от другого только по углам между

Рис. 14. Схема нараста-

ния граней кристалла

b с

их гранями. Основным методом диагностики кристаллических веществ в

те времена было измерение углов между гранями с помощью угломерного

прибора, так называемого гониометра (прикладного или отражательного).

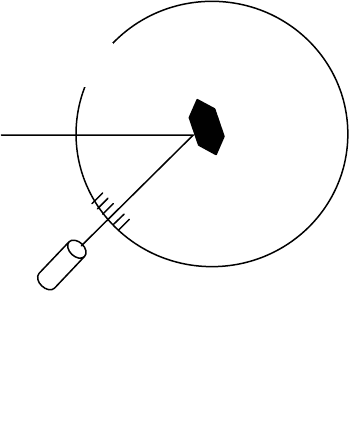
Принцип отражательного гониометра показан на рис. 16.

Луч света от источника S отража-

ется от грани кристалла К и попадает в

зрительную трубу О. Угол между па-

дающим и отраженным лучами измеря-

ется по шкале М, нанесенной на вра-

щающемся лимбе Р. Поворачивая кри-

сталл (или трубу), можно по отражени-

ям света от разных граней измерить уг-

лы между ними при помощи кругового

лимба с нониусом. В двухкружном го-

ниометре можно вращать кристалл од-

новременно вокруг двух взаимно пер-

пендикулярных осей. Точность измерения составляет порядка 1°. Для бо-

лее точных измерений существуют оптические (теодолитные) гониометры

(точность 0,25°). Например, кальцит (CaCO

) и доломит (CaCO

·МgСO

кристаллизующиеся в сходной ромбоэдрической форме, имеют углы меж-

ду смежными гранями 105°15' и 106°15' соответственно, т.е. провести ди-

агностику указанных минералов с большей надежностью можно лишь с

помощью теодолитного гониометра. Метод гониометрии не утратил своего

значения и в настоящее время.

Грани кристаллического многогранника соответствуют определен-

ным сеткам структуры, поэтому углы между гранями отвечают углам меж-

ду плоскими сетками в структуре кристалла. Теперь эти углы измеряют с

помощью рентгенограмм, для чего не обязательно иметь большой кри-

сталл с правильной внешней огранкой, а достаточно крупинки кристалли-

ческого вещества. Поскольку длины волн рентгеновских лучей соизмери-

мы по величине с межатомными расстояниями в кристаллических струк-

турах, кристаллы являются природными дифракционными решетками для

этих лучей. Именно с помощью дифракции рентгеновских лучей было до-

казано решетчатое строение кристаллов (М. Лауэ, 1912 г.).

Рис. 16. Схема измерения кри-

сталлов с помощью гониометра

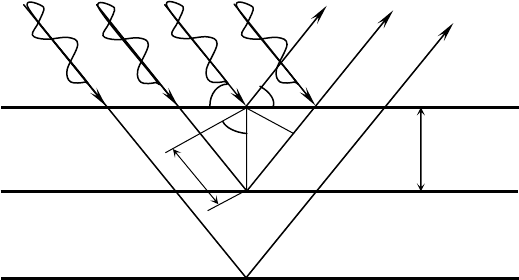
Схема, поясняющая дифракцию, дана на рис. 17: S

– пучок моно-

хроматических рентгеновских лучей, падающих под углом θ на семейство

параллельных атомных плоскостей, S – пучок дифрагированных лучей.

Рис. 17. Схема к выводу условия Вульфа - Брэгга

Дифрагированные лучи усиливают друг друга, если, согласно усло-

вию интерференции, разность хода ∆ между ними равна целому числу

длин волн, т.е.:

∆ = nλ (n = 1,2,3,…). (4)

Из чертежа видно, что разность хода между падающим и дифрагиро-

ванным лучами равна:

∆ = РО + ОQ = 2РО = 2 d sin θ. (5)

Чтобы волны, рассеянные двумя соседними плоскими сетками (а

значит, и всем семейством параллельных плоских сеток), дали максимум

интенсивности, необходимо выполнение основного закона дифракции

рентгеновских лучей в кристаллах:

2 d sin θ = nλ (n = 1,2,3,…). (6)

Это равенство выражает условие Вульфа - Брегга. Иначе говоря, если

луч с длиной волны λ падает на совокупность параллельных атомных

плоскостей, отстоящих друг от друга на расстоянии d, то он порождает

дифрагированный луч, идущий так, как шел бы луч, отраженный под уг-

лом θ. Таким образом, при определенных углах падения плоские сетки в

структуре кристалла могут "отражать" рентгеновские лучи. Эти отраже-

ния (точнее, максимумы интенсивности дифрагированных лучей) можно

зарегистрировать на фотографической пластинке или с помощью иони-

зационного спектрометра. Симметричный, закономерный узор на рент-

∆/2

генограмме отображает симметрию и закономерность структуры кри-

сталлического вещества и дает возможность измерять расстояния между

атомными плоскостями и углы между ними, которые на многогранных

формах кристаллов являются углами между гранями. По рентгенограм-

мам на основании условия (6) можно расшифровать структуры кристал-

лов, находить межплоскостные расстояния d, диагностировать кристал-

лические вещества.

3.2. Метод кристаллографического индицирования. Закон целых чисел

Как уже говорилось выше, кристаллографические системы коор-

динат, выбираемые в соответствии с симметрией кристалла, могут быть

и не прямоугольными. Кристаллическая решетка характеризуется ше-

стью параметрами элементарной ячейки: длинами ребер a, b, c и углами

α, β, γ (см. рис. 9), причем в общем случае a ≠ b ≠ c, α ≠ β ≠ γ ≠ 90°.

Для описания кристаллических многогранников и структур приме-

няется метод кристаллографического индицирования, удобный для всех

кристаллографических систем координат независимо от того, прямо-

угольные они или косоугольные, одинаковые у них масштабные отрезки

по осям или разные.

Символы узлов. Если один из узлов решетки выбрать за начало

координат, то любой другой узел решетки определяется радиусом-

вектором R = ma+nb+pc, где m, n, р – три числа, которые называют ин-

дексами данного узла. Совокупность чисел m, n, р, записанная в двой-

ных квадратных скобках [[mnр]], называется символом узла. Числа в

символе пишутся подряд, без запятых, читаются порознь. Запятые ста-

вятся лишь в тех (редчайших) случаях, когда индекс двузначен. Знак

минус пишется над цифрой.

Например, [[130]] читается "один, три, ноль", [[023]] – "ноль, минус два,

три".

На рис. 18 показаны символы некоторых узлов в плоской сетке (ин-

декс по оси Z равен нулю).

На рис. 19 показаны символы вершин, центров граней и центра эле-

ментарной ячейки, если одна из вершин ячейки принята за начало коорди-

нат. Дробные индексы применяются только в символах узлов; для симво-