Рябова М.С., Методические указания по эконометрике
Подождите немного. Документ загружается.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ В EXCEL
по дисциплине «Эконометрика»
Для решения задач в Excel используется надстройка Пакет анализа.
Запуск надстройки Пакет анализа выполняется с помощью команды Сервис |
Надстройки... В появившемся диалоговом окне Надстройки (рисунок 1) следует установить
флажок перед именем элемента Пакет анализа.
Рисунок 1
Если при выборе команды Сервис | Надстройки... элемент Пакет анализа не
появляется в списке надстроек, значит Пакет анализа не установлен. Его следует
установить с помощью программы SETUP.
1 Корреляционный анализ
Пример 1. Деятельность n=8 карьеров характеризуется себестоимостью 1т. песка
(X1),сменной добычей песка (X2) и фондоотдачей (X3). Значения показателей представлены
в таблице (рисунок 2).
Требуется: 1. Оценить параметры генеральной совокупности, которая
предполагается нормально распределенной.
Порядок вычислений следующий:
1) Введем исходные данные в файл с именем PRIMER в Excel, лист 1 (рисунок 2).
Рисунок 2
2) Рассчитаем точечные оценки (среднее, среднеквадратическое (стандартное)
отклонение и т.д.) для показателя X1.
Для этого через меню Сервис | Анализ данных... выберем инструмент Описательная
статистика и нажмем кнопку OK. На экране появится диалоговое окно Описательная
статистика (рисунок 3).
1
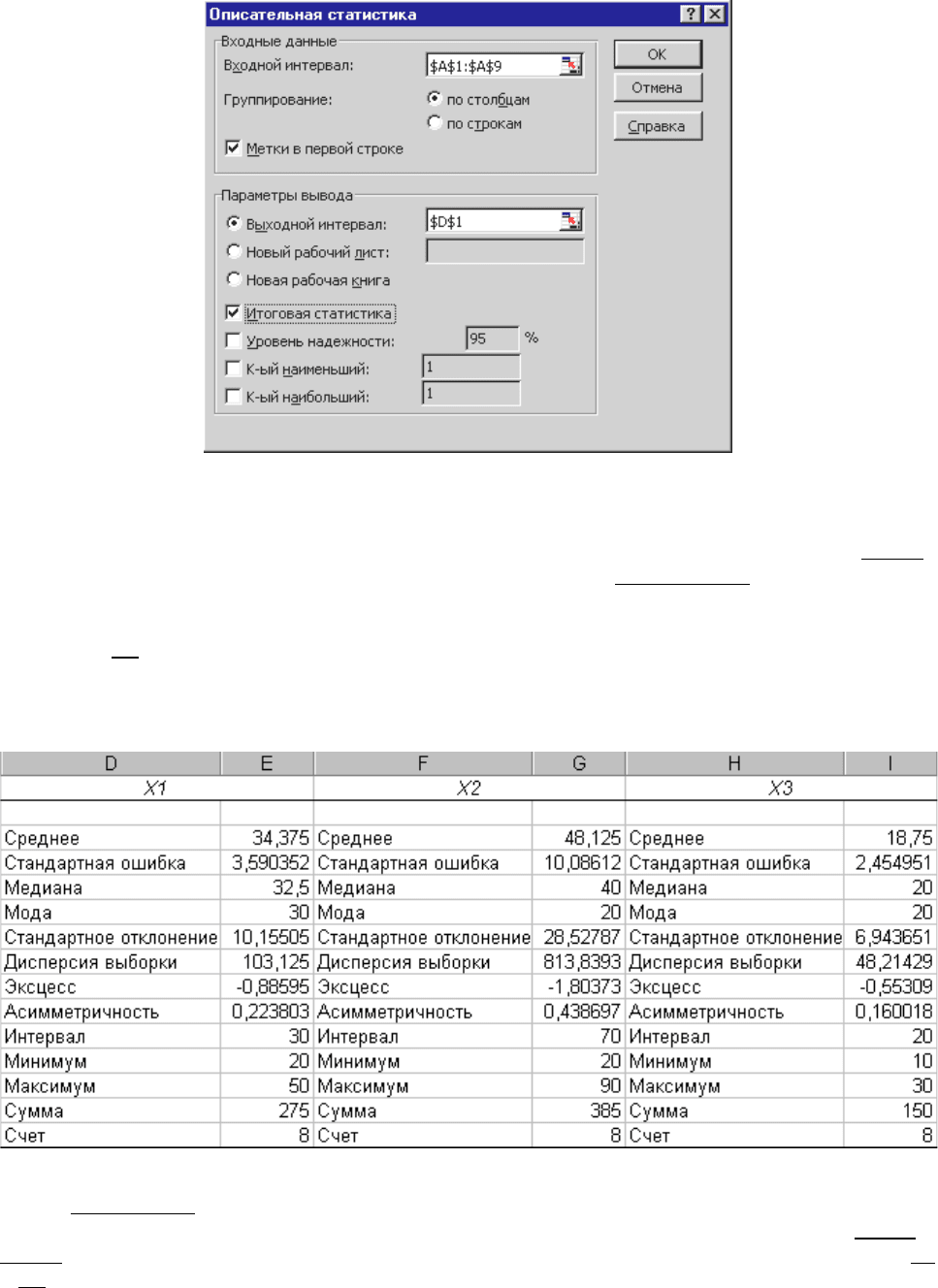
Рисунок 3
3) Заполним поля ввода данных и параметров вывода.
В поле Входной интервал введем ссылку на диапазон с исходными данными A 1: A 9 .
Оставим установку переключателя Группирование – по столбцам.
Установим опцию Метки – для вывода в первой строке названия столбца A.
В поле Выходной интервал введем адрес левой верхней ячейки будущего
диапазона D 1 .
Установим опцию Итоговая статистика – для получения дополнительной
информации. Нажмем кнопку OK.
Результаты вычислений показателя X1 представлены на рисунке 4.
Рисунок 4
Примечание. Для расчета точечных оценок показателей X2 и X3 по п.п. 2,3 в поле
Входной интервал необходимо ввести ссылку на диапазон с исходными данными B 1: B 9 и
C 1: C 9 , а в поле Выходной интервал – адрес левой верхней ячейки будущего диапазона F 1
и H 1 соответственно.
Как видно из таблицы описательных статистик (рисунок 4) результаты
автоматического расчета в Excel совпадают с ручным расчетом.
4) Рассчитаем парную корреляцию между показателями X1 и X2.
Для этого через меню Сервис | Анализ данных... выберем инструмент Корреляция
и нажмем кнопку OK. В диалоговом окне Корреляция заполним поля ввода данных и
параметров вывода согласно рисунку 5. Нажмем кнопку OK.
2
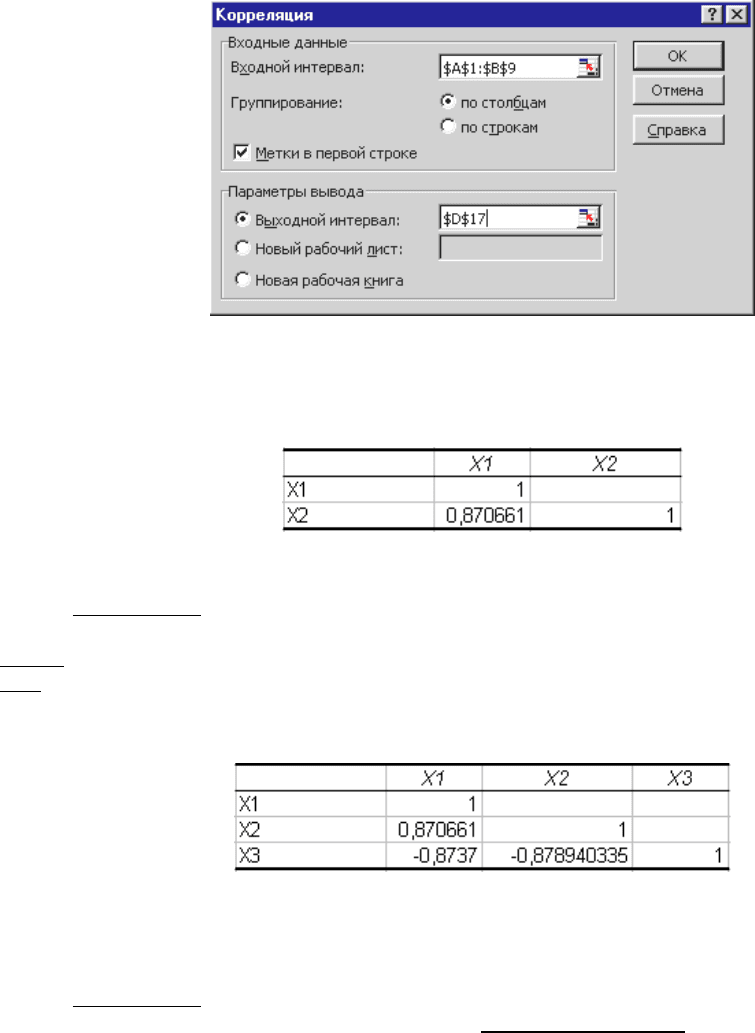
Рисунок 5
Результаты расчета в виде матрицы парных коэффициентов корреляции
представлены на рисунке 6.
Рисунок 6
Примечание. Для расчета парной корреляции между показателями X1, X2 и X3 по п. 4
в поле Входной интервал необходимо ввести ссылку на диапазон с исходными данными
A 1: C 9 , а в поле Выходной интервал – адрес левой верхней ячейки будущего диапазона
D 21 соответственно.
Результаты расчета в виде матрицы парных коэффициентов корреляции
представлены на рисунке 7.
Рисунок 7
Как видно из матриц коэффициентов парной корреляции (рисунки 6,7) результаты
автоматического расчета в Excel совпадают с ручным расчетом.
Примечание. Статистическая процедура Пакета анализа Корреляция пакета Excel
позволяет вычислять только коэффициенты парной корреляции без оценки значимости и
графической интерпретации полученных результатов. Для решения данного спектра задач
рекомендуется использовать пакет Statistica.
2 Регрессионный анализ
Пример 2. По данным n=20 сельскохозяйственных районов требуется построить
регрессионную модель урожайности на основе следующих показателей:
Y – урожайность зерновых культур (ц/га);
X1 – число колесных тракторов (приведенной мощности) на 100 га;
X2 – число зерноуборочных комбайнов на 100 га;
X3 – число орудий поверхностной обработки почвы на 100 га;
X4 – количество удобрений, расходуемых на гектар;
X5 – количество химических средств оздоровления растений, расходуемых на гектар.
Исходные данные для анализа приведены в таблице (рисунок 8).
Порядок вычислений следующий:
1) Введем исходные данные в файл с именем PRIMER в Excel, лист 2 (рисунок 8).
3

Рисунок 8
2) Предварительно, с целью анализа взаимосвязи показателей построим матрицу
парных коэффициентов корреляции.
Для этого выберем через меню Сервис | Анализ данных... инструмент Корреляция и
нажмем кнопку OK. В диалоговом окне Корреляция заполним поля ввода данных и
параметров вывода согласно рисунку 9.
Рисунок 9
Результаты расчета в виде матрицы парных коэффициентов корреляции
представлены на рисунке 10.
Рисунок 10
4
Анализ матрицы парных коэффициентов корреляции показывает, что
результативный показатель Y наиболее тесно связан с показателем X4 – количеству
удобрений, расходуемых на гектар (r
y4
=0.57).
В то же время связь между признаками-аргументами достаточно тесная. Так,
существует практически функциональная связь между числом колесных тракторов (X1) и
числом орудий поверхностной обработки почвы (X3) – r
13
=0.98.
О наличие мультиколлинеарности свидетельствуют также коэффициенты корреляции
r
12
=0.85 и r
32
=0,88.
3) Чтобы продемонстрировать отрицательное влияние мультиколлинеарности,
построим регрессионную модель, включив в нее все исходные показатели.
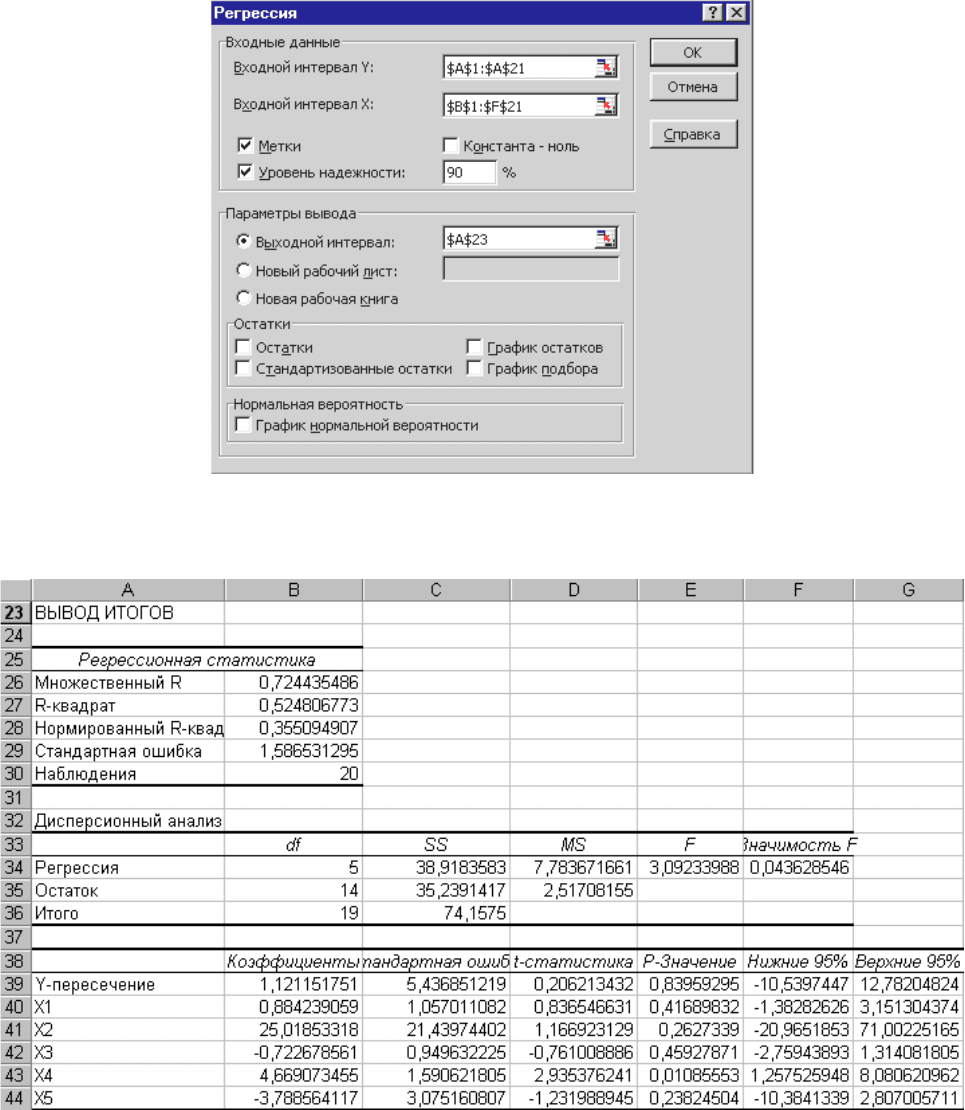
Для этого выберем через меню Сервис | Анализ данных... инструмент Регрессия и
нажмем кнопку OK. В диалоговом окне Регрессия заполним поля ввода данных и
параметров вывода согласно рисунку 11. Нажмем кнопку OK.
Рисунок 11
Результаты регрессионного анализа представлены на рисунке 12.
Рисунок 12
5
Согласно рисунку 12 регрессионная модель имеет вид:
Ŷ = 1.121 + 0.884X1 + 25.019X2 – 0.723X3 + 4.670X4 – 3.789X5 (2.1)
(0.21) (0.84) (1.17) (-0.76) (2.94) (-1.23)
В скобках указаны t
набл
(b
j
), расчетные значения t–критерия для проверки гипотезы о
значимости коэффициента регрессии H
0
: β
j
=0, j=1, 2, 3, 4, 5. Критическое значение t
кр
=1.76
найдено по таблице t–распределения при уровне значимости α=0.1 и числе степеней
свободы ν =14. Из уравнения следует, что статистически значимым является коэффициент
регрессии только при X4, т.к. |t
4
|=2.94>t
кр
=1.76.
Не поддаются экономической интерпретации отрицательные знаки коэффициентов
регрессии при X3 и X5, из чего следует, что повышение числа орудий поверхностной
обработки почвы на 100 га (X3) и количества химических средств оздоровления растений
(X5) отрицательно сказывается на урожайности. Таким образом, полученное уравнение
регрессии не приемлемо.
После реализации алгоритма пошагового регрессионного анализа с исключением
переменных (в Excel не выполняется) и учетом того, что в уравнение должна войти только
одна из трех тесно связанных переменных (X1, X2 или X3) получаем окончательное
уравнение регрессии:
Ŷ = 7.342 + 0.345X1 + 3.294X4 (2.2)
(11.12) (2.09) (3.02)
4) Проверим регрессионное уравнение (2.2) в Excel.
Для этого скопируем исходные данные X1 в диапазон ячеек H1:H21, а X4 – в диапазон ячеек
I1:I21. Далее через меню Сервис | Анализ данных... выберем инструмент Регрессия и
нажмем кнопку OK. В диалоговом окне Регрессия заполним поля ввода данных и
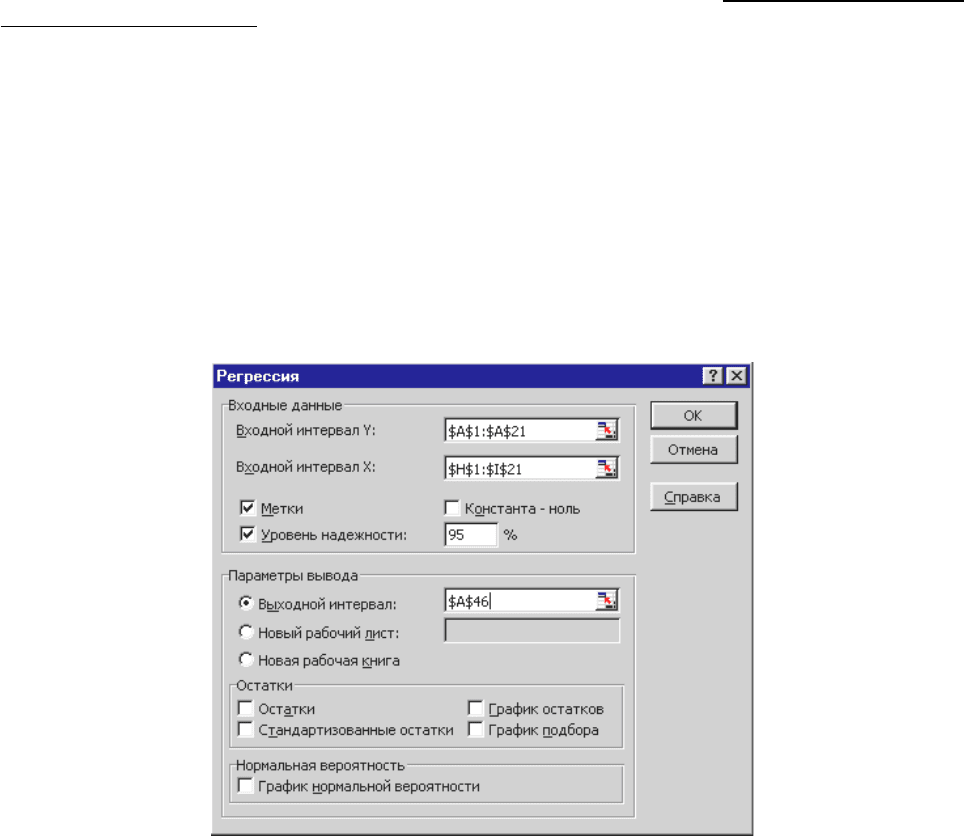
параметров вывода согласно рисунку 13. Нажмем кнопку OK.
Рисунок 13
Результаты регрессионного анализа представлены на рисунке 14. Уравнение
регрессии, рассчитанное в Excel, незначительно отличается от (2.2) и имеет вид:
Ŷ = 7.300 + 0.349X1 + 3.413X4 (2.3)
(10.76) (2.10) (2.98)
Оценку значимости уравнения регрессии проведем по (2.3).
В уравнение (2.3) включен X1, как определяющий из трех показателей.
Уравнение значимо при α=0.05, т.к. F
набл
=7.36>F
кр
=3.20, найденного по таблице F-
распределения при α=0.05; ν
1
=3 и ν
2
=17. Значимы и все коэффициенты регрессии β
1
и β
4
в
уравнении |t
j
|>t
кр
(α=0.05; v=17) = 2.11. Коэффициент регрессии β
1
следует признать
6
значимым (β
1
≠0) из экономических соображений при этом t
1
=2.10 лишь незначительно
меньше t
кр
=2.11. При α=0.1 t
кр
=1.74 и β
1
статистически значим.
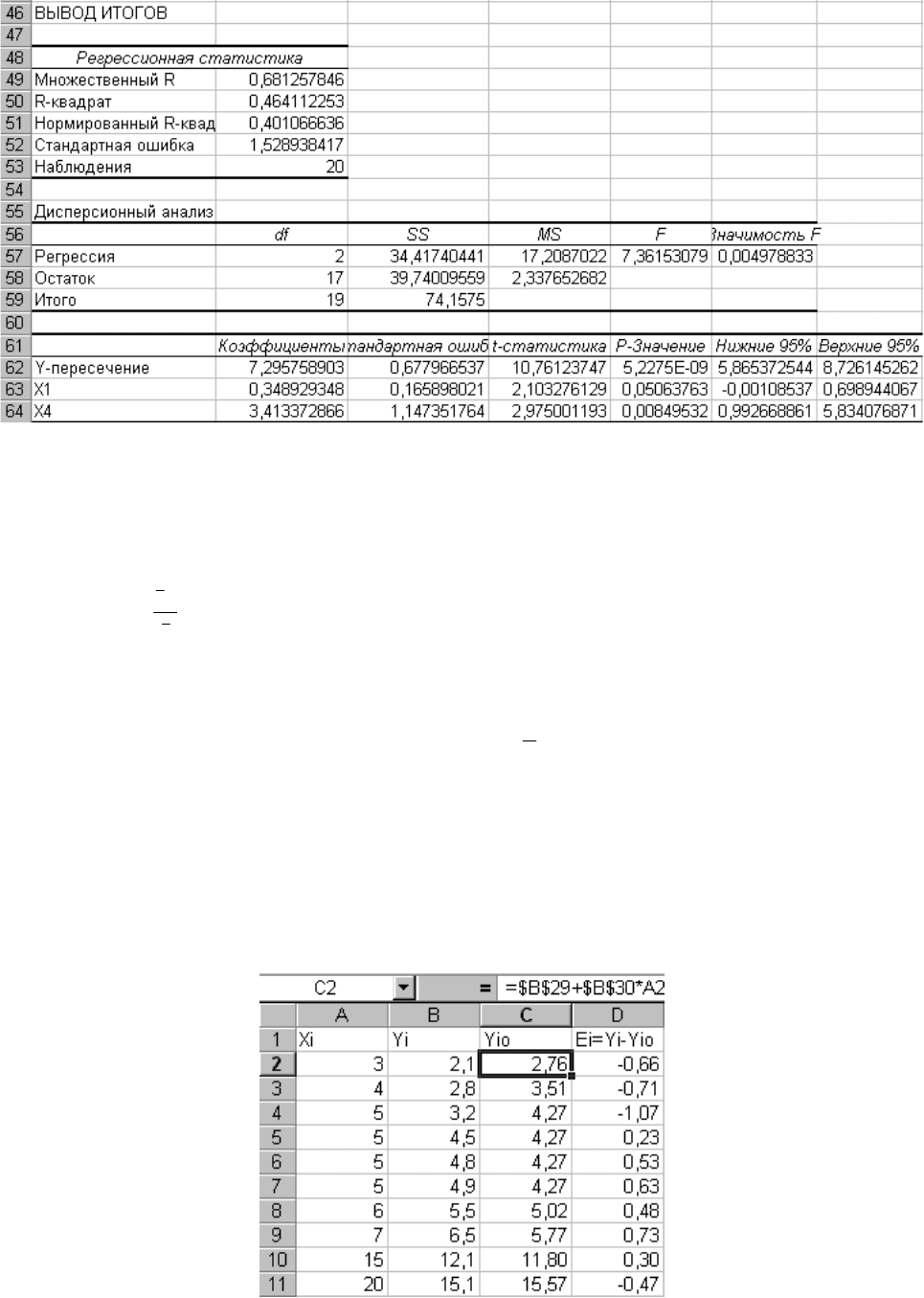
Рисунок 14
Из уравнения регрессии следует, что увеличение на 1 числа тракторов на 100 га
пашни приводит к росту урожайности зерновых в среднем на 0.349 ц/га (b
1
=0.349).
Коэффициенты эластичности Э
1
=0.068 и Э
4
=0.161 показывают, что увеличение
показателей Х
1
и Х
4
на 1% урожайность зерновых повышается соответственно на 0.068% и
0.161% (
y
j
x
j
b
j
Э
).
Множественный коэффициент детерминации r
y
2
=0.464 свидетельствует о том, что
только 46.4% вариации урожайности объясняется вошедшими в модель показателями (Х
1
и
Х
4
), т.е. насыщенностью растениеводства тракторами и удобрениями. Остальная часть
вариации обусловлена действием неучтенных факторов (Х
2
, Х
3
, Х
5
, погодных условий и др.).
Средняя относительная ошибка аппроксимации
10.5% характеризует адекватность
модели, также как и величина остаточной дисперсии S
2
=2.34.
Пример 3. По данным годовых отчетов десяти (n=10) машиностроительных
предприятий провести регрессионный анализ зависимости производительности труда y
(млн. руб. на чел.) от объема производства х (млрд. руб.). Предполагается линейная
модель, т.е.
x
10
~
.
Порядок вычислений следующий:
1) Введем исходные данные в файл с именем PRIMER в Excel, лист 3 (рисунок 15).
Рисунок 15
7
2) С целью качественного анализа взаимосвязи показателей построим диаграмму
рассеяния.
Порядок построения следующий:
2.1) выделим диапазон ячеек A1:B11;
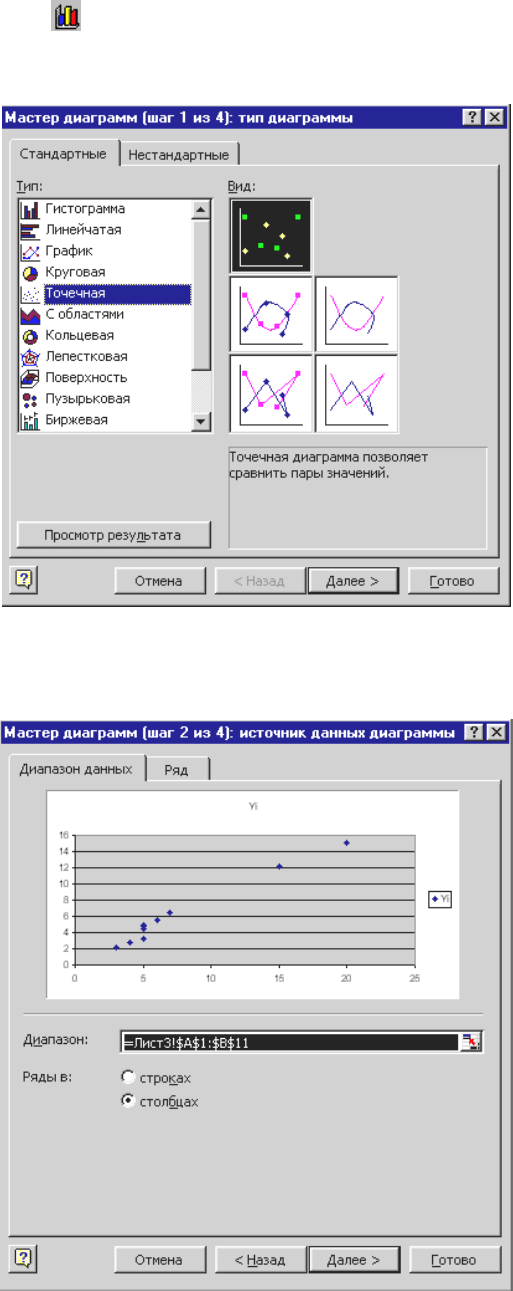
2.2) нажмем кнопку - Мастер диаграмм панели Стандартная;
2.3) в окне Тип укажем Точечная (рисунок 16), вид графика отметим в поле со
списком типов. Нажмем кнопку Далее;
Рисунок 16
2.4) так как диапазон данных заполнен (рисунок 17), нажмем кнопку Далее;
Рисунок 17
2.5) заполним параметры диаграммы согласно рисунку 18. Нажмем кнопку Далее;
8

Рисунок 18
2.6) укажем место размещения диаграммы на имеющемся листе (рисунок 19).
Нажмем кнопку Далее.
Рисунок 19
Готовая диаграмма рассеяния изучаемых показателей представлена на рисунке 20.
Рисунок 20
Из диаграммы видно, что зависимость близка к линейной – прямая хорошо
аппроксимирует данные.
3) Построим регрессионную модель двух показателей.
Для этого выберем через меню Сервис | Анализ данных... инструмент Регрессия и
нажмем кнопку OK. В диалоговом окне Регрессия заполним поля ввода данных и
параметров вывода согласно рисунку 21. Нажмем кнопку OK.
Результаты регрессионного анализа представлены на рисунке 22.
Оценка уравнения регрессии имеет вид:
Ŷ = 0.50092 + 0.75321X.
Перейдем к статистическому анализу полученного уравнения регрессии: проверке
значимости уравнения и его коэффициентов, исследованию абсолютных е
i
= y
i
– ŷ и
относительных
i
ii
i
y
yy
ˆ
ошибок аппроксимации
9

Рисунок 21
Рисунок 22
Согласно рисунку 22 несмещенная оценка остаточной дисперсии равна:
Ŝ
2
= 0.486055046, а оценка среднеквадратического отклонения Ŝ = 0.697176481.
Проверим на уровне значимости α=0.05 значимость уравнения регрессии, т.е.
гипотезу H
0
:β=0 (β
0
=β
1
=0). Согласно рисунку 21 F
набл
= 318.063892. По таблице F-
распределения для α=0.05, ν
1
= 2 и ν
2
= 8 находим Fкр=4.46. Так как F
набл
>Fкр, то
уравнение является значимым.
Для проверки значимости коэффициента регрессии, т.е. гипотезы H
0
:β
1
=0, находим
по таблице t-распределения при α=0.05, ν = 8 значение t
кр
=2,31, а согласно рисунку 21
t
набл
(b
1
) = 17.8343.
Так как t
набл
(b
1
) = 17.8343> t
кр
=2,31, то коэффициент регрессии β
1
значимо отличается
от нуля.
Таким образом, окончательное уравнение регрессии имеет вид:
Ŷ = 0.50092 + 0.75321X.
Интервальные оценки коэффициентов уравнения с доверительной вероятностью
0.95 согласно рисунку 21 составляют:
-0.389 ≤ β
0
≤ 1.391 и
0.656 ≤ β
1
≤ 0.851.
10
