Robertson C.R. Fundamental electrical and electronic principles
Подождите немного. Документ загружается.


D.C. Circuits
51
that there are only two ‘ unknowns ’ to fi nd, namely I
1
and I
2
. The
value for the third branch current, I
3
, is then simply found by using
the values obtained for I
1
and I
2
.
3 If a negative value is obtained for a current then the minus sign
MUST be retained in any subsequent calculations. However, when
you quote the answer for such a current, make a note to the effect
that it is fl owing in the opposite direction to that marked, e.g. from
C to D.
4 When tracing the path around a loop, concentrate solely on that
loop and ignore the remainder of the circuit. Also note that if you
are following the marked direction of current then the resulting
p.d.(s) are assigned positive values. If the direction of ‘ travel ’ is
opposite to the current arrow then the p.d. is assigned a negative
value.
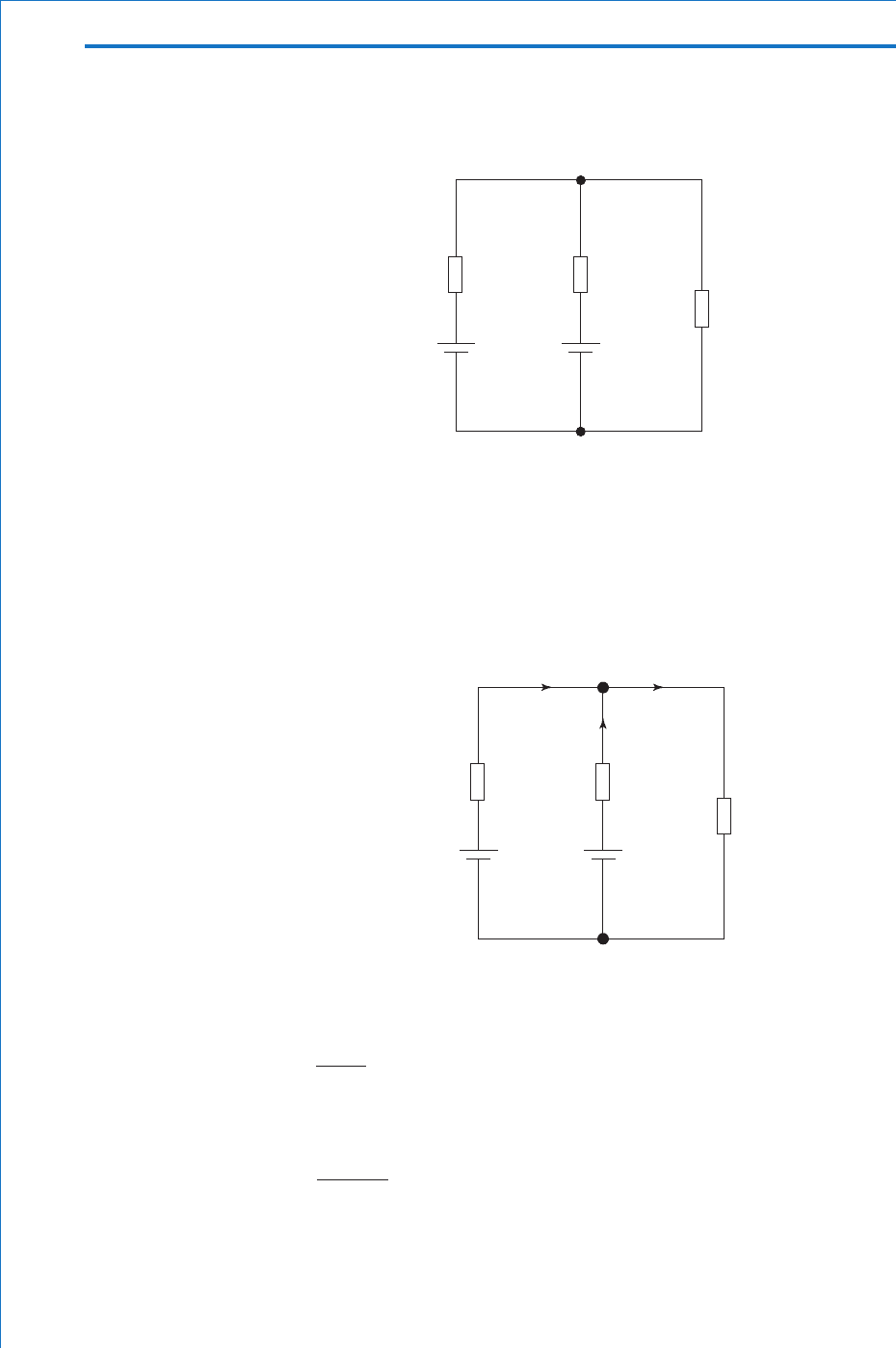
Let us now apply these techniques to the circuit of Fig. 2.18 .
Consider fi rst the left-hand loop in a clockwise direction. Tracing
around the loop it can be seen that there is only one source of emf
within it (namely E
1
). Thus the sum of the emfs is simply E
1
volt.
Also, within the loop there are only two resistors ( R
1
and R
2
) which
will result in two p.d.s, I
1
R
1
and ( I
1
I
2
)R
3
volt. The resulting loop
equation will therefore be:
ABEFA: EIRIIR
111 123
()
[1]
Now taking the right-hand loop in a counterclockwise direction it can
be seen that again there is only one source of emf and two resistors.
This results in the following loop equation:
CBEDC: EIR IIR
222 123
()
[2]
Finally, let us consider the loop around the edges of the diagram in a
clockwise direction. This follows the ‘ normal ’ direction for E
1
but is
opposite to that for E
2
, so the sum of the emfs is E
1
E
2
volt. The loop
equation is therefore
ABCDEFA: EE IRIR
121122
[3]
Since there are only two unknowns then only two simultaneous
equations are required, and three have been written. However it is a
useful practice to do this as the ‘ extra ’ equation may contain more
convenient numerical values for the coeffi cients of the ‘ unknown ’
currents.
The complete technique for the applications of Kirchhoff ’ s laws
becomes clearer by the consideration of a worked example containing
numerical values.
52
Fundamental Electrical and Electronic Principles
Worked Example 2.9
Q For the circuit of Fig. 2.19 determine the value and direction of the current in each branch, and the p.d.
across the 10 resistor.
10 Ω
2 Ω3 Ω
10 V
4 V
I
1
I
2
(I
1
I
2
)
ABC
FED
Fig. 2.20
A
The circuit is rst labelled and current ows identi ed and marked by applying
the current law. This is shown in Fig. 2.20 .
R
1
E
2
E
1
R
2
R
3
10 Ω
2 Ω3 Ω
10 V
4 V
Fig. 2.19
ABEFA :
1
1
1
1
043 2
63 2
2
2
II
IIso ……………[]
ABCDEFA :
11
1
11 1
1
1
1
03 0
3010
03 0 2
22
22
2
III
III
II
()
[]so ……………
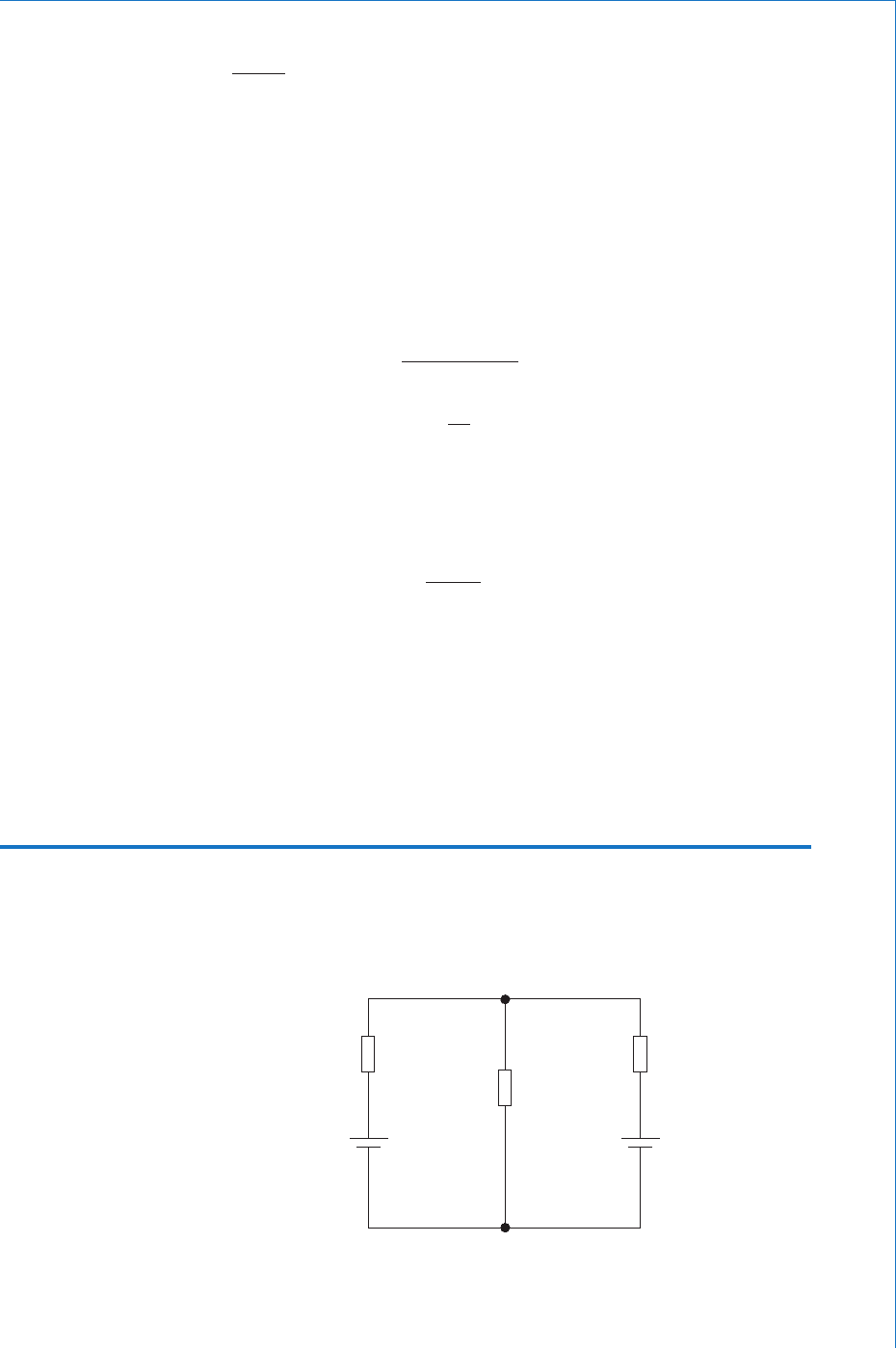
D.C. Circuits
53
BCDEB :
42 0
2010
40 2 3
22
22
2
III
III
II
1
1
11
1
1
1
()
[]so ……………
Inspection of equations [1] and [2] shows that if equation [1] is multiplied by 5
then the coe cient of I
2
will be the same in both equations. Thus, if the two are
now added then the term containing I
2
will be eliminated, and hence a value
can be obtained for I
1
.
30 5 0 5
03 0 2
40 28
2
2
11 1
11 1
1
1
1
II
II
I
……………
……………
[]
[]
so I
1
40
28
1.429 A Ans
Substituting this value for I
1
into equation [3] yields;
44292
24429
029
2
0 857
2
2
2
11
11
1
1
.
.
.
.
I
I
Iso A (charge) Anns
(). . .
()
.
II
II
1
1
2
22
429 0 857 0 572
0 572
A
volt
Ans
VR
CD CD
110
572so V V
CD
. Ans
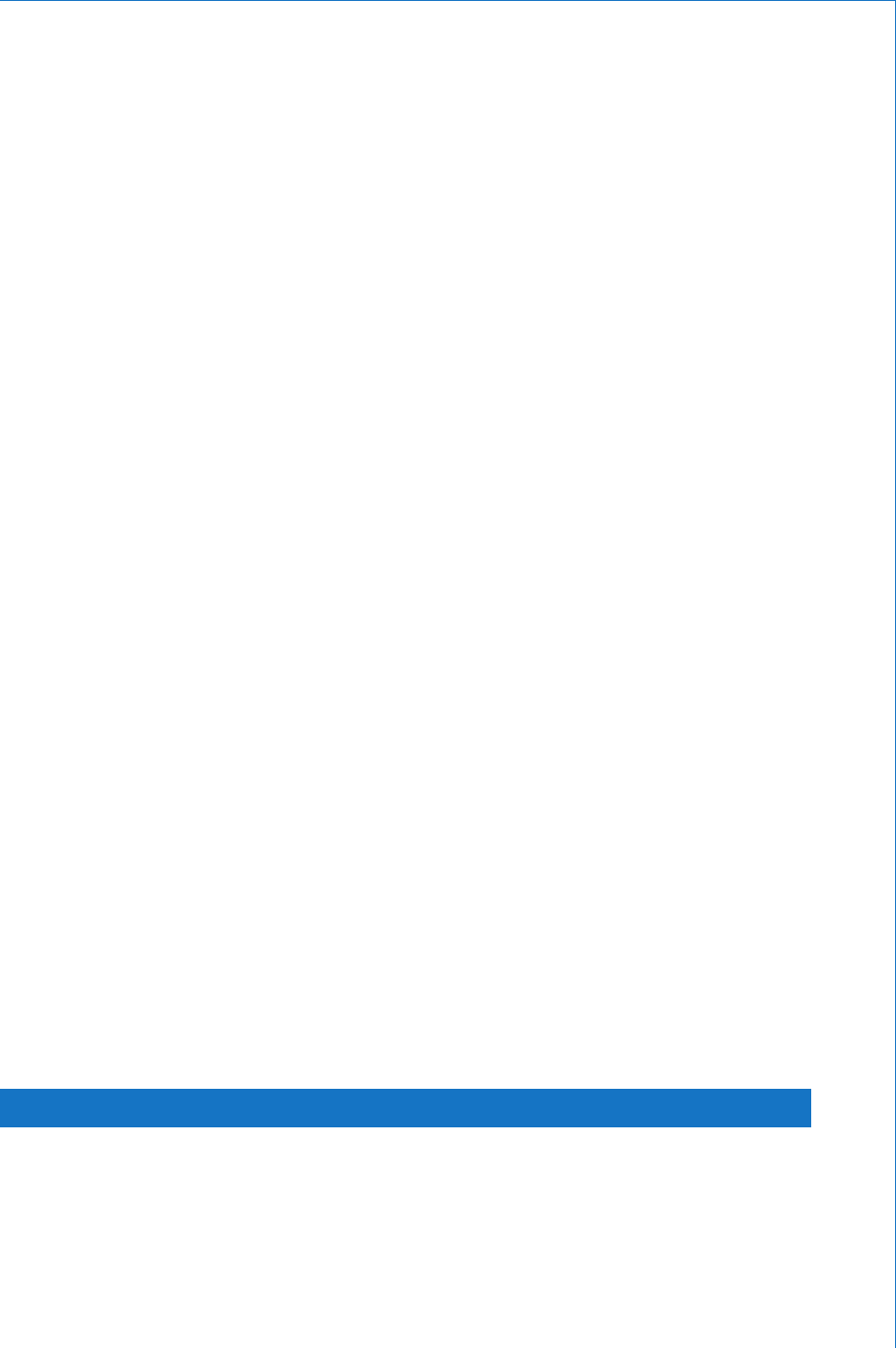
Worked Example 2.10
Q For the circuit shown in Fig 2.21 , use Kirchho ’ s Laws to calculate (a) the current owing in each
branch of the circuit, and (b) the p.d. across the 5 resistor.
5 Ω
1.5 Ω 2 Ω
6 V
4.5 V
Fig. 2.21

54
Fundamental Electrical and Electronic Principles
A
Firstly the circuit is sketched and labelled and currents identi ed using
Kirchho ’ s current law. This is shown in Fig. 2.22 .
1.5 Ω
5 Ω
R
3
2 Ω
R
2
R
1
(I
1
I
2
)
6 V 4.5 V
E
1
E
2
I
1
I
2ABC
FED
Fig. 2.22
(a) We can now consider three loops in the circuit and write down the
corresponding equations using Kirchho ’ s voltage law:
ABEFA:
ER R
111 1
11 11
11
III
I II III
()
.().
23
22
655 555
6
volt
so, 665 5
2
.[]II
1
1 ……………
CBEDC:
ER R
222 23
222 2
4525 255
45
III
IIIIII
()
.()
.
1
11
volt
so, 557 2
2
II
1
……………[]
ABCDEFA:
EE R R
111
1
1
1
11
222
2
2
645 5 2
552
II
II
II
volt
so,
..
.. […………… 33]
Now, any pair of these three equations may be used to solve the problem,
using the technique of simultaneous equations. We shall use equations [1]
and [3] to eliminate the unknown current I
2
, and hence obtain a value for
current I
1
. To do this we can multiply [1] by 2 and [3] by 5, and then add the
two modi ed equations together, thus:
11 1 1
1
1
1
1
23 0 2
75 75 0 3 5
95 205
2
2
II
II
I
……………
……………
..[ ]
.. []
..
11
1
1
1hence, A I
95
20 5
095
.
.
. Ans
D.C. Circuits
55
Substituting this value for I
1
into equation [3] gives:
11 1
11
11
.(. .)
..
...
550952
5 427 2
2 427 5 0 07
2
2
2
I
I
Ihence, 332
0 0366
2
and A I . Ans
Note: The minus sign in the answer for I
2
indicates that this current is
actually owing in the opposite direction to that marked in Fig. 2.22 . This
means that battery E
1
is both supplying current to the 5 resistor and
charging battery E
2
.
Current through 5 resistor amp
so cu
II
1
1
2
0 95 0 0366.(.)
rrrent through 5 resistor A 0 95 0 0366 0 9 4.. .11Ans
(b) To obtain the p.d. across the 5 resistor we can either subtract the p.d.
(voltage drop) across R
1
from the emf E
1
or add the p.d. across R
2
to emf
E
2
, because E
2
is being charged. A third alternative is to multiply R
3
by the
current owing through it. All three methods will be shown here, and,
provided that the same answer is obtained each time, the correctness of
the answers obtained in part (a) will be con rmed.
VE R
V
BE
BE
111
11
1
I volt
so, V
6095 5
6 4265
4 574
(. .)
.
. Ans
OR:
volt
so,
VE R
V
BE
BE
222
4 5 0 0366 2
4 5 0 0732
4 573
I .(. )
..
.VV Ans
OR:
VR
V
BE
BE
() .
.
II
1
1
23
09 4 5
457
volt
so, V Ans
The very small di erences between these three answers is due simply
to rounding errors, and so the answers to part (a) are veri ed as
correct.
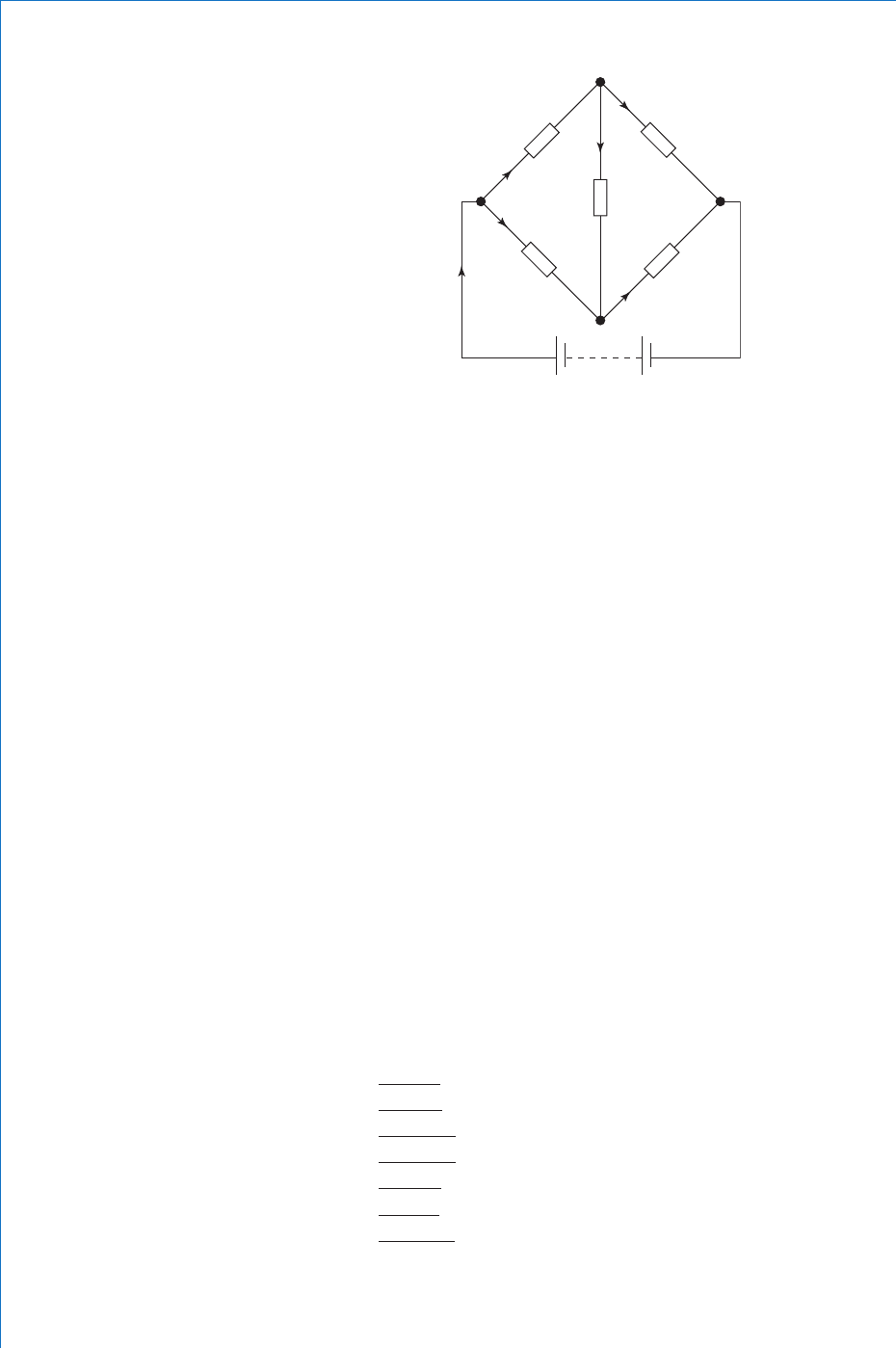
2.8 The Wheatstone Bridge Network
This is a network of interconnected resistors or other components,
depending on the application. Although the circuit contains only one
source of emf, it requires the application of a network theorem such
as the Kirchhoff ’ s method for its solution. A typical network, suitably
labelled and with current fl ows identifi ed is shown in Fig. 2.23 .
56
Fundamental Electrical and Electronic Principles
Notice that although there are fi ve resistors, the current law has been
applied so as to minimise the number of ‘ unknown ’ currents to three.
Thus only three simultaneous equations will be required for the
solution, though there are seven possible loops to choose from. These
seven loops are:
ABCDA; ADCA; ABDCA; ADBCA; ABDA; BCDB; and
ABCDA
If you trace around these loops you will fi nd that the last three do not
include the source of emf, so for each of these loops the sum of the
emfs will be ZERO! Up to a point it doesn ’ t matter which three loops
are chosen provided that at least one of them includes the source.
If you chose to use only the last three ‘ zero emf ’ loops you would
succeed only in proving that zero equals zero!
The present level of study does not require you to solve simultaneous
equations containing three unknowns. It is nevertheless good practice
in the use of Kirchhoff’s laws, and the seven equations for the above
loops are listed below. In order for you to gain this practice it is
suggested that you attempt this exercise before reading further, and
compare your results with those shown below.
ABCA : E
1
I
1
R
1
( I
1
I
3
) R
3
ADCA : E
1
I
2
R
2
( I
2
I
3
) R
4
ABDCA : E
1
I
1
R
1
I
3
R
5
( I
2
I
3
) R
4
ADBCA : E
1
I
2
R
2
I
3
R
5
( I
1
I
3
) R
3
ABDA : 0 I
1
R
1
I
3
R
5
I
2
R
2
BCDB : 0 ( I
1
I
3
) R
3
( I
2
I
3
) R
4
I
3
R
5
ABCDA : 0 I
1
R
1
( I
1
I
3
) R
3
( I
2
I
3
) R
4
I
2
R
2
(I
1
I
3
)
(I
2
I
3
)
R
2
R
4
R
1
R
5
R
3
C
A
I
1
I
2
I
E
1
I
3
D
B
Fig. 2.23
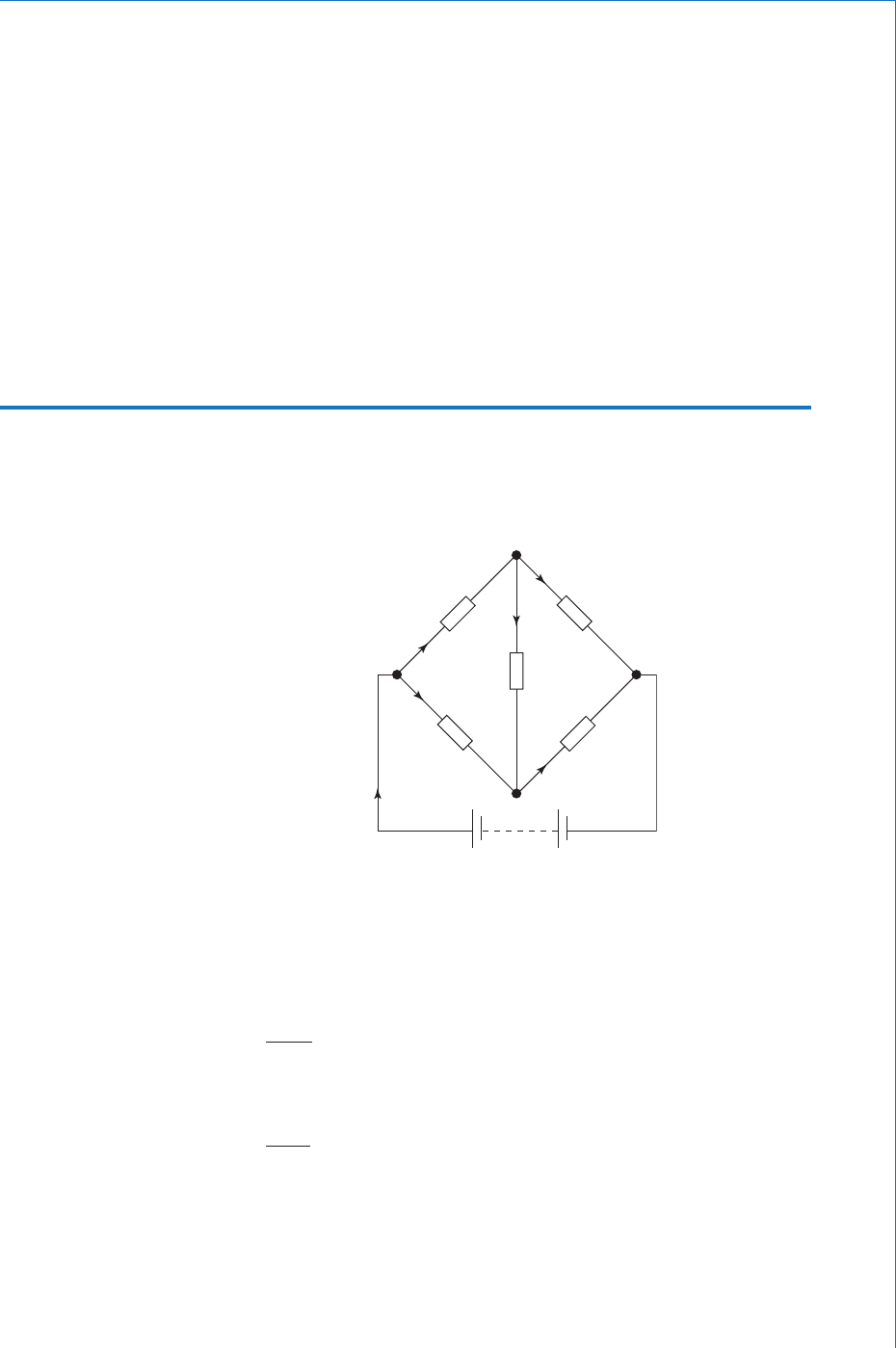
D.C. Circuits
57
As a check that the current law has been correctly applied, consider
junctions B and C:
current arriving at B
total current leaving
so
I
II
II
12
1
II
II II
IIII
II
2
13 23
1323
12
current arriving at C
()()
I
Hence, current leaving battery current returning to battery.
Worked Example 2.11
Q For the bridge network shown in Fig. 2.24 calculate the current through each resistor, and the current
drawn from the supply.
(I
1
I
3
)
(I
2
I
3
)
5 Ω
3 Ω
1 Ω
6 Ω 4 Ω
C
A
I
1
I
2
I
10 V
I
3
D
B
Fig. 2.24
A
The circuit is rst labelled and the currents identi ed using the current law as
shown in Fig. 2.24 .
ABDA :
06 5 3
06 3 5 1
32
23
III
III
1
1
……………[]
BDCB :
05 4
544
04 0
323 3
323 3
23
III II
III I I
II I
1
1
1
1
1
()()
………………[]2

58
Fundamental Electrical and Electronic Principles
ADCA :
11
1
03
3
04 3
223
223
23
III
III
II
()
……………[]
Multiplying equation [1] by 2, equation [2] by 3 and then adding them
0260 2
02330 23
03
23
23
2
11 1
1
1
1
II I
II I
I
……………
……………
[]
[]
440 4
3
I ……………[]
Multiplying equation [3] by 3, equation [4] by 4 and then adding them
30 2 3 3 3
02 60 44
30 63
30
23
23
3
3
1
11
1
1
II
II
I
I
……………
……………
[]
[]
663
084 .1 A Ans
Substituting for I
3
in equation [3]
11
1
1
04 084
4986
98 6
4
2 454
2
2
2
I
I
I
.
.
.
. A Ans
Substituting for I
3
and I
2
in equation [2]
0 4 2 454 84
4 4 294
4 294
4
074
I
I
I
1
1
1
1
1
..
.
.
. A Ans
II I
I
1
1
2
074 2 454
3 529
..
. A Ans
Since all of the answers obtained are positive values then the currents will
ow in the directions marked on the circuit diagram.
Worked Example 2.12
Q If the circuit of Fig. 2.24 is now amended by simply changing the value of R
DC
from 1 t o 2 , calculate
the current owing through the 5 resistor in the central limb.
A
The amended circuit diagram is shown in Fig. 2.25 .
ABDA :
06 5 3
06 3 5
32
23
III
III
1
1
1……………[]

D.C. Circuits
59
(I
1
I
3
)
(I
2
I
3
)
5 Ω
3 Ω
2 Ω
6 Ω 4 Ω
C
A
I
1
I
2
10 V
I
3
D
B
Fig. 2.25
BDCB :
052 4
52244
042
323 3
323 3
23
III II
IIIII
II I
()()
1
1
1
11 ………………[]2
Multiplying equation [1] by 2, equation [2] by 3 and adding them
0260 2
02633 23
043
23
23
3
11 1
1
1
1
II I
II I
I
……………
……………
[]
[]
soo A I
3
0 Ans
At fi rst sight this would seem to be a very odd result. Here we have a
resistor in the middle of a circuit with current being drawn from the
source, yet no current fl ows through this particular resistor! Now, in any
circuit, current will fl ow between two points only if there is a difference
of potential between the two points. So we must conclude that the
potentials at junctions B and D must be the same. Since junction A is
a common point for both the 6 and 3 resistors, then the p.d. across
the 6 must be the same as that across the 3 resistor. Similarly, since
point C is common to the 4 and 2 resistors, then the p.d. across
each of these must also be equal. This may be verifi ed as follows.
Since I
3
is zero then the 5 resistor plays no part in the circuit. In this
case we can ignore its presence and re-draw the circuit as in Fig. 2.26 .
Thus the circuit is reduced to a simple series/parallel arrangement that
can be analysed using simple Ohm ’ s law techniques.
RRR
R
I
E
R
I
V
ABC
ABC
ABC
AB
13
1
1
64
10
10
10
1
ohm
so
amp
so A
IR
11
16 6 volt V
60
Fundamental Electrical and Electronic Principles
Similarly,
A
and V
R
I
V
ADC
AD
32 5
10
5
2
236
2
Thus V
AB
V
AD
6 V, so the potentials at B and D are equal. In
this last example, the values of R
l
, R
2
, R
3
and R
4
are such to produce
what is known as the
balance condition for the bridge. Being able to
produce this condition is what makes the bridge circuit such a useful
one for many applications in measurement systems. The value of
resistance in the central limb has no effect on the balance conditions.
This is because, at balance, zero current fl ows through it. In addition,
the value of the emf also has no effect on the balance conditions, but
will of course affect the values for I
1
and I
2
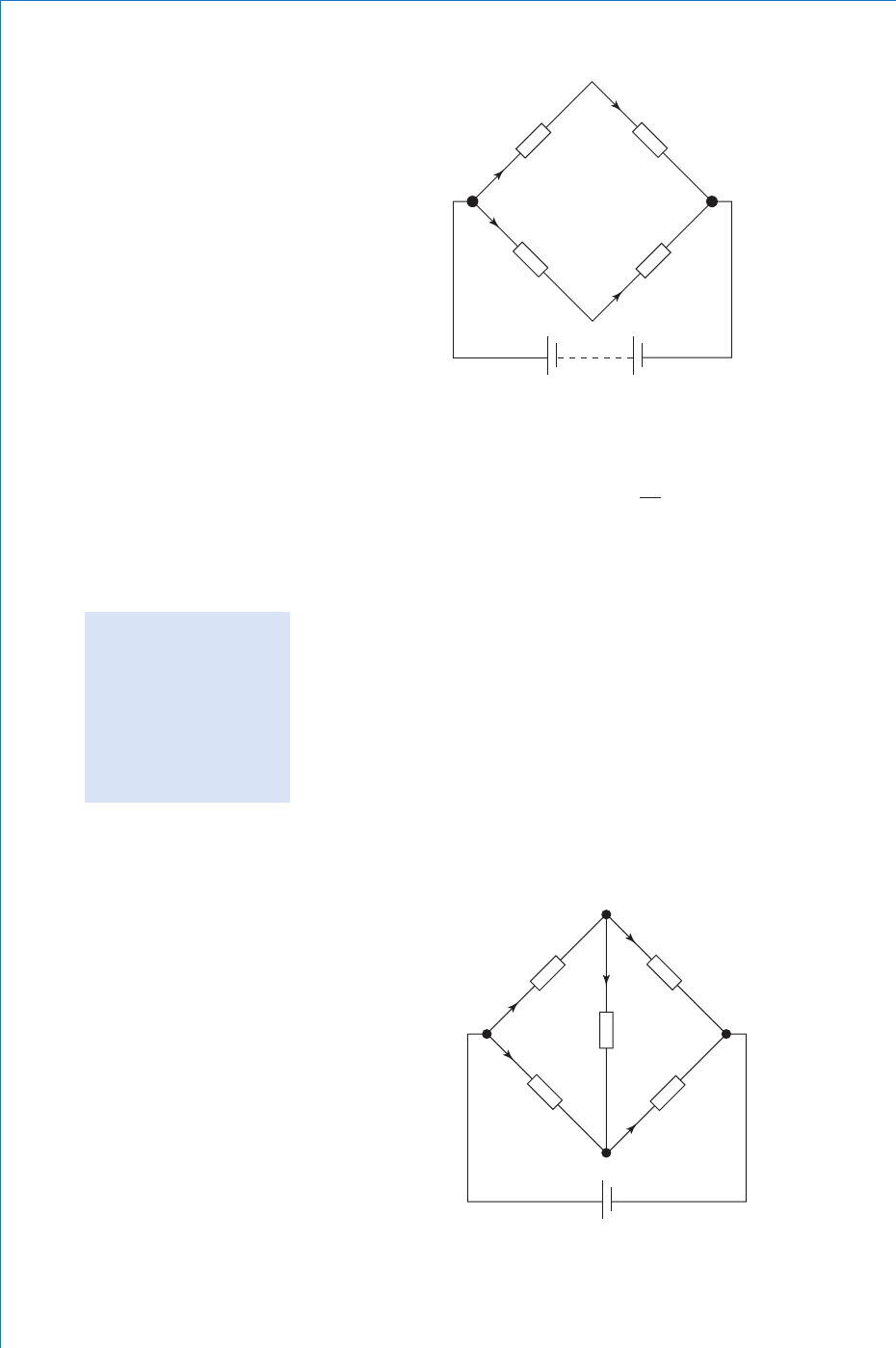
. Consider the general case
of a bridge circuit as shown in Fig. 2.27 , where the values of resistors
R
1
to R
4
are adjusted so that I
3
is zero.
Balance condition refers
to that condition when zero
current fl ows through the
central arm of the bridge
circuit, due to a particular
combination of resistor
values in the four ‘ outer ’
arms of the bridge
(I
1
I
3
)
(I I
3
)
R
5
R
2
R
4
R
1
R
3
C
A
I
1
I
2
E
I
3
D
B
Fig. 2.27
I
1
I
2
3 Ω
2 Ω
6 Ω 4 Ω
C
A
I
1
R
1
R
2
R
3
R
4
I
2
10 V
D
B
Fig. 2.26
