Robertson C.R. Fundamental electrical and electronic principles
Подождите немного. Документ загружается.

91
(a)
C
CC
CC
C
1
1
1
2
2
64
64
24
0
24
farad
microfarad
so F . Ans
(b)
QVC
Q
coulomb
so C
1150 2 4 0
360
6
.
Ans
(same charge on both)
C
1
V
1
V
V
2
C
2
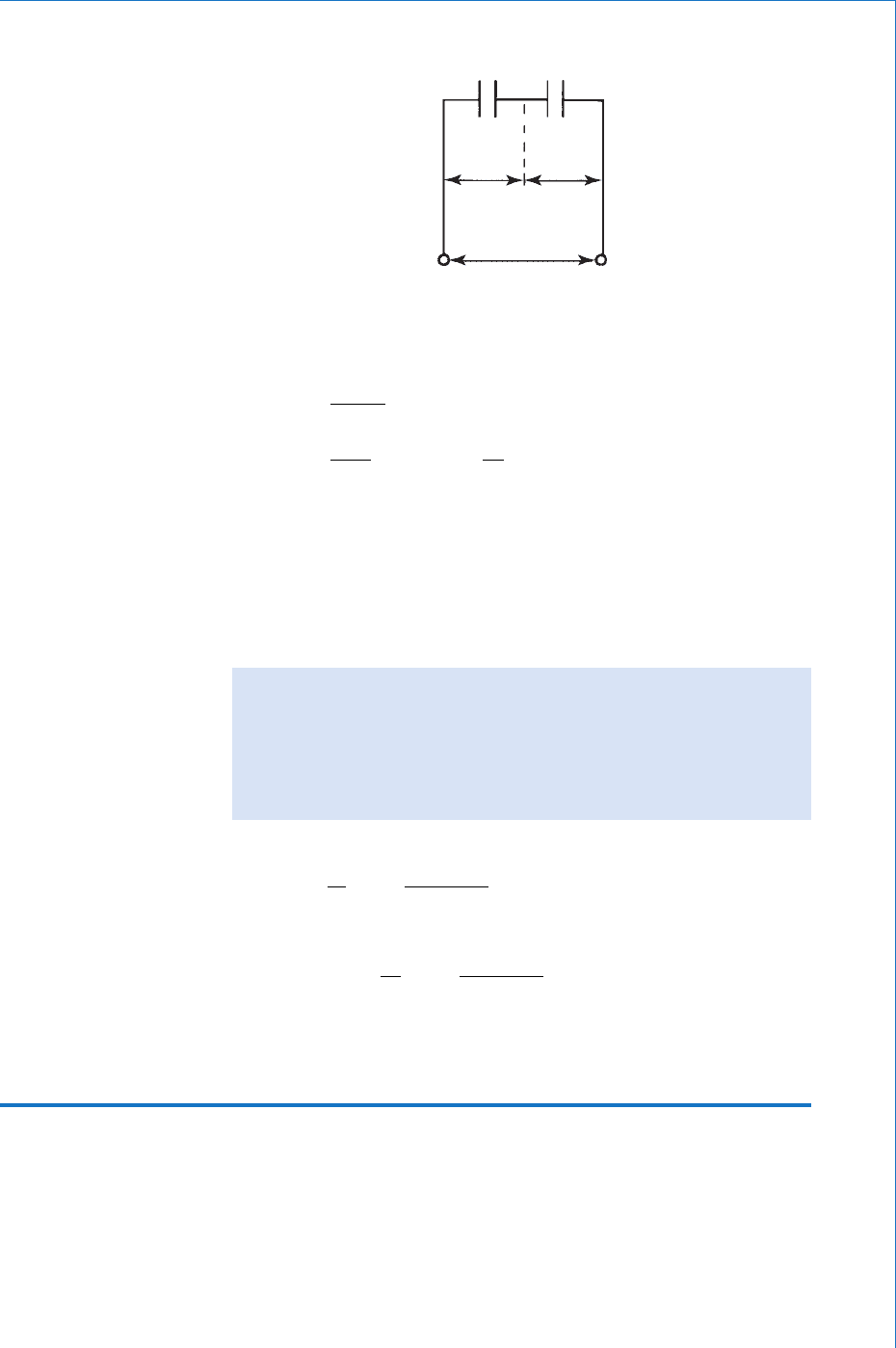
6 μF4μF
150 V
Fig. 3.12
Since capacitors in series all receive the same value of charge, then this must
be the total charge drawn from the supply,
QVC
This is equivalent to a series resistor circuit where the current drawn from
the supply is common to all the resistors
(c)
V
Q
C
V
1
1
1
1
1
volt
so V
360 0
60
60
6
6
Ans
Similarly, volt
so
Note tha
V
Q
C
V
2
2
6
6
2
360 0
40
90
1
1
V Ans
tt VV V
1
1
2
50 V
Worked Example 3.11
Q Capacitors of 3 F, 6 F and 12 F are connected in series across a 400 V supply. Determine the p.d.
across each capacitor.
A
Figure 3.13 shows the relevant circuit diagram.
Electric Fields and Capacitors
92
Fundamental Electrical and Electronic Principles
C
1
3 F; C
2
6 F; C
3
12 F; V 400 V
1111111
1
1
11
1
11
1
CC C C
C
QVC
23
36 2
42
2
7
2
2
7
74so F
co
.
uulomb
C
volt
400 7 4 0
685 7
685 7 0
30
6
6
6
11 1
1
1
1
1
.
.
.
Q
V
Q
C
sso V V
1
228 6. Ans
Similarly, V
and
V
V
2
6
6
3
6
685 7 0
60
43
685 7 0
.
.
.
1
1
11
1
Ans
112 0
57
6
1
1.V Ans
3.14 Series/Parallel Combinations
The techniques required for the solution of this type of circuit are again
best demonstrated by means of a worked example.
Worked Example 3.12
Q For the circuit shown in Fig. 3.14 , determine (a) the charge drawn from the supply, (b) the charge on
the 8 F capacitor, (c) the p.d. across the 4 F capacitor, and (d) the p.d. across the 3 F capacitor.
C
1
C
2
C
3
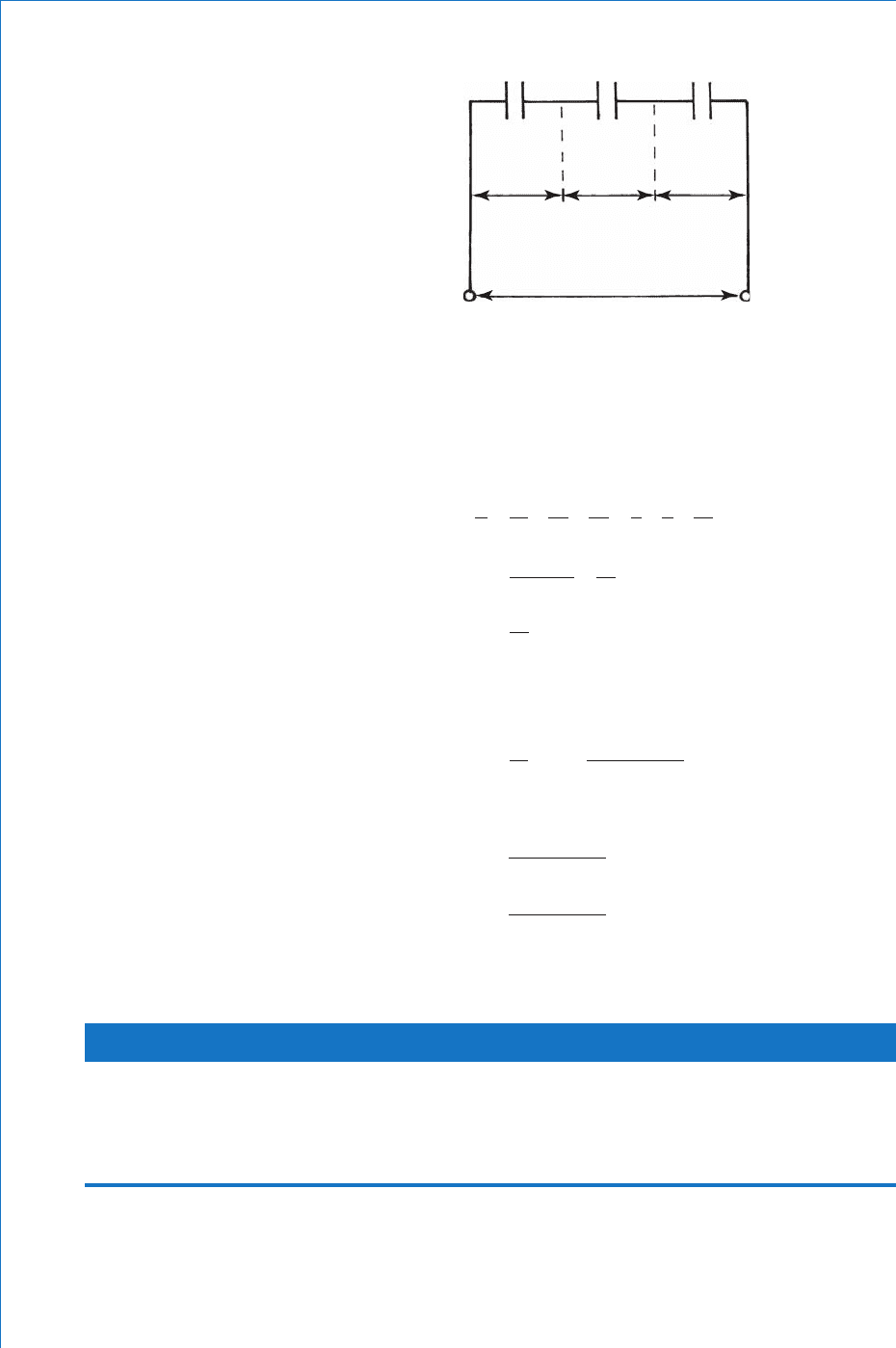
3 μF6μF12μF
V
1
V
2
V
3
V
400 V
Fig. 3.13

93
A
The rst task is to label the diagram as shown in Fig. 3.15 .
2 μF
3 μF6μF
4 μF
8 μF
200 V
Fig. 3.14
2 μF
3 μF6μF
4 μF
8 μF
200 V
A
E
B
C
D
F
Fig. 3.15
2 μF
2 μF
4 μF
8 μF
AD
FE
B
200 V
Fig. 3.16
Electric Fields and Capacitors
(a)
C
C
BCD
BD
36
36
236
246 37
F (see Fig. )
F (see Fig. )
.
.
1
1

94
Fundamental Electrical and Electronic Principles
1.5 μF
8 μF
AD
FE
200 V
Fig. 3.18
C
CC C
C
Q
AD
AD EF
62
62
538
58
95
11
1
..
.
.
F (see Fig. )
so F
VC
Q
coulomb
hence, mC
200 9 5 0
9
6
.
.
1
1 Ans
2 μF6μF
8 μF
AD
B
EF
200 V
Fig. 3.17
(b)
QVC
Q
EF EF
EF
coulomb
so mC
200 8 0
6
6
1
1. Ans
(c) Total charge Q 1.9 mC and Q
EF
1. 6 m C
so Q
AD
1.9 1.6 0.3 mC (see Fig. 3.18 ).
and referring to Fig. 3.17 , this will be the charge on both the capacitors
shown, i.e.
QQ
AB BD
03.mC.
Thus, V
BD
p.d. across 4 F capacitor (see Fig. 3.16 )
V
Q
C
V
BD
BD
BD
BD
03 0
60
50
3
6
. 1
1
volt
so V Ans
Electric Fields and Capacitors
95
(d)
QVC
BCD BD BCD
(see Figs and )
C
36 35
50 2 0
00
6
..11
1
1
and this will be the charge on both the 3 F and 6 F capacitors, i.e.
QQ
V
Q
C
V
BC CD
BC
BC
BC
BC
1
11
1
00
0
30
33 33
4
6
C
Thus volt
so . VV Ans
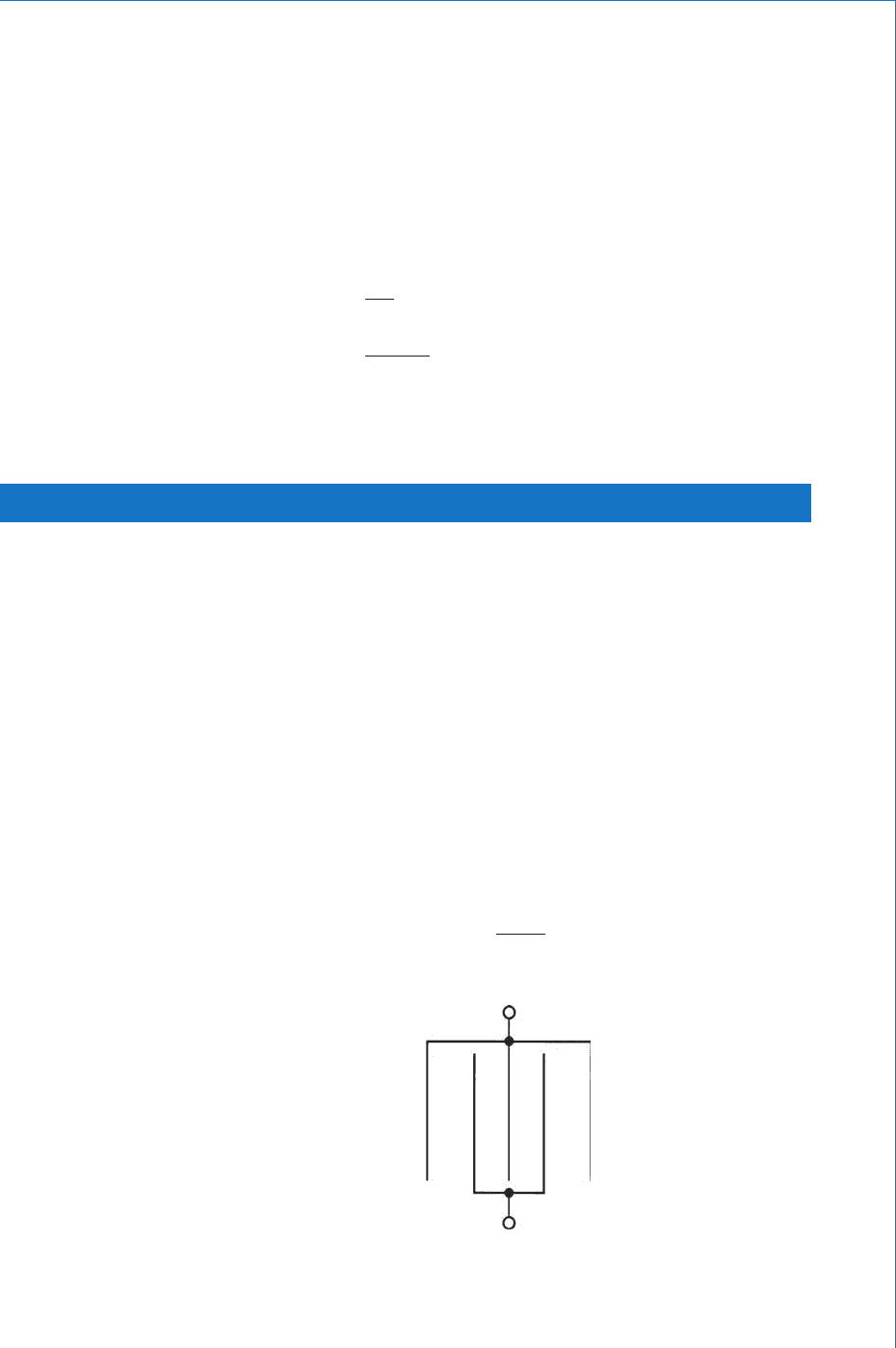
3.15 Multiplate Capacitors
Most practical capacitors consist of more than one pair of parallel
plates, and in these cases they are referred to as multiplate capacitors.
The sets of plates are often interleaved as shown in Fig. 3.19 . The
example illustrated has a total of fi ve plates. It may be seen that this
effectively forms four identical capacitors, in which the three inner
plates are common to the two ‘ inner ’ capacitors. Since all the positive
plates are joined together, and so too are the negative plates, then this
arrangement is equivalent to four identical capacitors connected in
parallel, as shown in Fig. 3.20 . The total capacitance of four identical
capacitors connected in parallel is simply four times the capacitance
of one of them. Thus, this value will be the effective capacitance of the
complete capacitor.
The capacitance between one adjacent pair of plates will be
C
A
d
1
εε
or
farad
Fig. 3.19

96
Fundamental Electrical and Electronic Principles
C
AN
d
1
1
εε
or
farad
()
(3.16)
so, the total for the complete arrangement C
1
4, but we can
express 4 as (5 1) so the total capacitance is
C
A
d
1
51
εε
or
farad
()
C
1
C
2
C
3
C
4
Fig. 3.20
In general therefore, if a capacitor has N plates, the capacitance is
given by the expression:
Since the above equation applies generally, then it must also apply to
capacitors having just one pair of plates as previously considered. This
is correct, since if N 2 then ( N 1) 1, and the above equation
becomes identical to equation (3.12) previously used.
Worked Example 3.13
Q A capacitor is made from 20 interleaved plates each 80 mm by 80 mm separated by mica sheets
1.5 mm thick. If the relative permittivity for mica is 6.4, calculate the capacitance.
A
N 20; A 80 80 10
6
m
2
; d 1.5 10
3
m; ε
r
6.4
C
AN
d
1
1
1
111
11
εε
or
farad
s
()
..
.
8 854 0 6 4 6400 0 9
50
26
3
oo nF C 46. Ans
Worked Example 3.14
Q A 300 pF capacitor has nine parallel plates, each 40 mm by 30 mm, separated by mica of relative
permittivity 5. Determine the thickness of the mica.
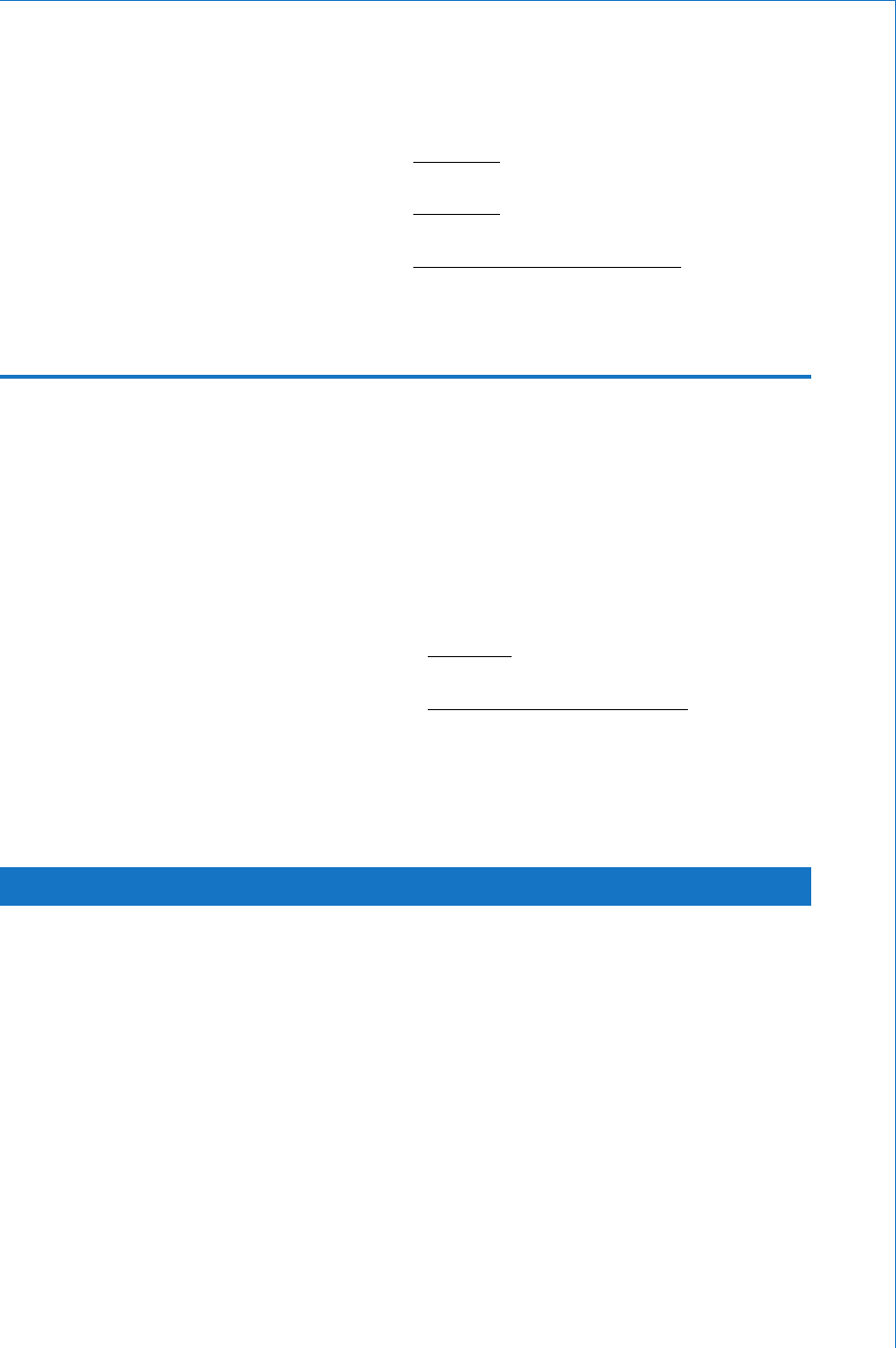
Electric Fields and Capacitors
97
A
N 9; C 3 10
10
F; A 40 30 10
6
m
2
; ε
r
5
C
AN
d
d
AN
C
εε
εε
or
or
farad
metre
()
()
.
1
1
11
1
8 854 0 5 200
2
11
1
1
1
08
30
42
6
0
so mm d . Ans
Worked Example 3.15
Q A parallel plate capacitor consists of 11 circular plates, each of radius 25 mm, with an air gap of 0.5 mm
between each pair of plates. Calculate the value of the capacitor.
A
N 11; r 25 10
3
m; d 5 10
4
m; ε
r
1(air)
Ar
A
C
An
d
22 32
32
25 0
9635 0
metre
so, m
or
()
.
()
1
11
1εε
ffarad
thus,
8 854 0 9635 0 0
50
348 0
23
4
0
..
.
11 11
1
1
1
1
C FF or pF 348 Ans
3.16 Energy Stored
When a capacitor is connected to a voltage source of V volts we have
seen that it will charge up until the p.d. between the plates is also V
volts. If the capacitor is now disconnected from the supply, the charge
and p.d. between its plates will be retained.
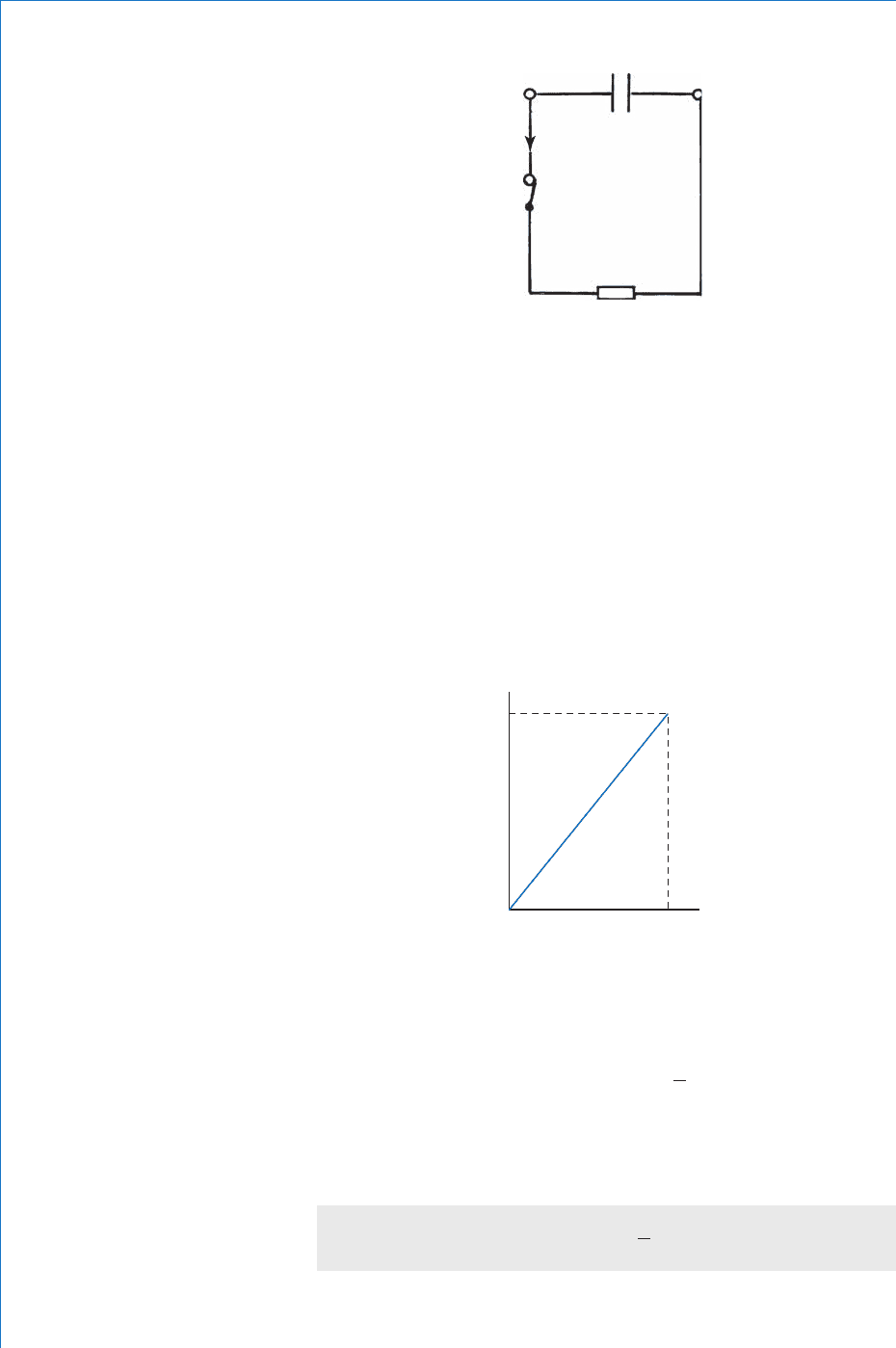
Consider such a charged capacitor, as shown in Fig. 3.21 , which now
has a resistor connected across its terminals. In this case the capacitor
will behave as if it were a source of emf. It will therefore drive current
through the resistor. In this way the stored charge will be dissipated as
the excess electrons on its negative plate are returned to the positive
plate. This discharge process will continue until the capacitor becomes
completely discharged (both plates electrically neutral). Note that the
discharge current marked on the diagram indicates conventional
current fl ow.
98
Fundamental Electrical and Electronic Principles
so energy stored, jouleWCV
1
2
2
(3.17)
However, if a discharge current fl ows then work must be done (energy
is being dissipated). The only possible source of this energy in these
circumstances must be the capacitor itself. Thus the charged capacitor
must store energy.
If a graph is plotted of capacitor p.d. to the charge it receives, the area
under the graph represents the energy stored. Assuming a constant
charging current, the graph will be as shown in Fig. 3.22 .
p.d. (volt)
V
0Q
charge
(coulomb)
Fig. 3.22
The area under the graph
but coulomb
1
2
QV
QCV
V
I
R
Fig. 3.21

Electric Fields and Capacitors
99
Worked Example 3.16
Q A 3 μ F capacitor is charged from a 250 V d.c. supply. Calculate the charge and energy stored. The
charged capacitor is now removed from the supply and connected across an uncharged 6 F capacitor.
Calculate the p.d. between the plates and the energy now stored by the combination.
A
C
1
3 F; V
1
250 V; C
2
6 F
QVC
Q
WCV
11
11
1
11
coulomb
so mC
joule
250 3 0
075
2
6
2
. Ans
22
3 0 250
93 75
62
1
so mJ W . Ans
When the two capacitors are connected in parallel the 3 F will share its charge
with 6 F capacitor. Thus the total charge in the system will remain unchanged,
but the total capacitance will now be di erent:
Total capacitance, farad
so F
volt
CC C
C
V
Q
C
1 2
36
9
75
.
11
1
1
0
90
83 33
2
4
6
2
so V
total energy stored, jou
V
WCV
. Ans
ll e
so mJ
1
1
1
2
9 0 83 33
325
62
.
.W Ans
Note: The above example illustrates the law of conservation of charge,
since the charge placed on the fi rst capacitor is simply redistributed
between the two capacitors when connected in parallel. The total
charge therefore remains the same. However, the p.d. now existing
between the plates has fallen, and so too has the total energy stored.
But there is also a law of conservation of energy, so what has happened
to the ‘ lost ’ energy? Well, in order for the 3 F capacitor to share its
charge with the 6 F capacitor a charging current had to fl ow from one
to the other. Thus this ‘ lost ’ energy was used in the charging process.
Worked Example 3.17
Q
Consider the circuit of Fig. 3.23 , where initially all three capacitors are fully discharged, with the
switch in position ‘ 1 ’ .
(a) If the switch is now moved to position ‘ 2 ’ , calculate the charge and energy stored by C
1
.
(b) O n c e C
1
is fully charged, the switch is returned to position ‘ 1 ’ . Calculate the p.d. now existing
across C
1
and the amount of energy used in charging C
2
and C
3
from C
1
.

100
Fundamental Electrical and Electronic Principles
A
(a)
QVC
Q
WCV
11
1
11
11
1
coulomb
so, mC
joule
20000
2
2
0
6
2
Ans
.55 0 200
02
52
1
1
so, J W . Ans
(b) C
2
and C
3
in series is equivalent to
C
CC
CC
4
23
23
microfarad
so, FC
4
68 47
68 47
278
..
..
.
and total capacitance of the whole circuit,
CC C
C
1
1
1
4
0278
278
microfarad
hence, F
.
.
Now, the charge received by the circuit remains constant, although the total
capacitance has increased.
Thus, volt
and V
V
Q
C
V
20
278 0
56 5
3
6
1
11
1
.
. Ans
Total energy remaining in the circuit, jouleWCV
1
1
2
05
2
.2278 0 565
056
62
..
.
11
1and JW
the energy used up must be the di erence between the energy rst stored
by C
1
and the nal energy stored in the system, hence
Energy used 0.2 0.156 4 4 m J Ans
C
2
C
3
C
1
6.8 μF
10 μF
4.7 μF
V
200 V
‘1’
‘2’
Fig. 3.23
