Рихтер Л.А. и др. Вспомогательное оборудование ТЭС (распознан)

Подождите немного. Документ загружается.

Пружинные

подвески

должны иметь достаточно длинные тя-

ги для обеспечения свободы горизон-

тальных перемещений соответствую-

щих точек трасс

Минимальная длина тяги зависит

от величины горизонтального пере-

мещения точки крепления трубопро-

вода, а максимальная определяется,

как правило, компоновочными воз-

можностями.

Для пружинных подвесок и опор

применяют цилиндрические винто-

вые пружины, работающие на кру-

чение.

Основной характеристикой пру-

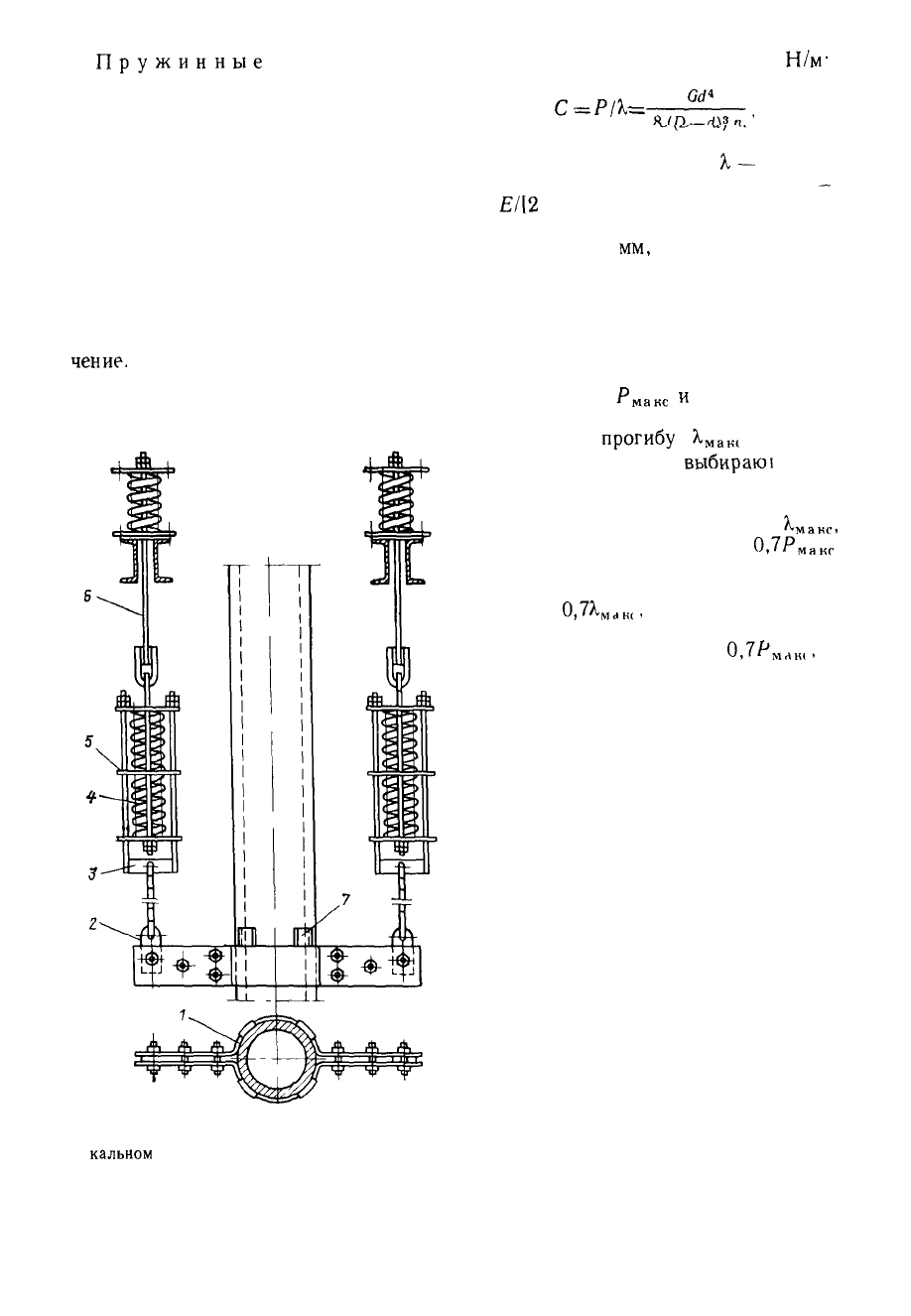
Рис 6 3 Пружинная подвеска на верти

кальном

участке трубопровода с двумя це-

пями пружин и с тремя последовательными

пружинами в каждой цепи

/ — хомут, 2 — ушко, 3 — траверса, 4 — пружина,

5 — направляющая тарелка, 6 — тяга 7 — упор

жины является ее жесткость С,

Н/м"

РА

__^1_,

(6 14)

где Р — нагрузка, Н,

К—

прогиб

вдоль оси пружины, мм; Е и G —

Е1\2

(1 + v)l — модули упругости

и сдвига пружинной стали, d — диа-

метр прутка,

мм,

D — наружный

диаметр пружины, мм; п — число ра-

бочих витков, v — коэффициент Пу-

ассона

Пружины для опор и подвесок

трубопроводов стандартизованы (ОСТ

764.04-78), различаются по допусти-

мой нагрузке

ма

кс

подразделяют-

ся на две группы (70 и 140 мм) по мак-

симальному

ПрОГибу

^маж

Обычно пружины

выбираюi

и ре

гулируют таким образом, чтобы в

рабочем состоянии трубопровода их

деформация не превышала 0,7

MaKC

а нагрузка была не более

0,7Р

макг

Если вертикальное температурное пе-

ремещение данной точки трассы пре-

вышает

0,7k

MdHI

устанавливают две

и более пружин в цепи Если нагруз-

ка на опору превышает

0,7Р

млш

ус-

танавливают две и более параллель-

ных цепей пружин Последовательное

включение пружин в цепи понижает

жесткость опоры пропорционально

количеству последовательных пружин,

при этом во столько же раз увели-

чивается допускаемое вертикальное пе-

ремещение трубопровода в точке опо-

ры Параллельное включение пру-

жинных цепей повышает жесткость

и грузоподъемность опоры пропор-

ционально числу цепей На рис 6 3

приведена пружинная подвеска с дву-

мя цепями пружин и с тремя по-

следовательными пружинами в каж-

дой цепи

При температурных перемещениях

паропроводных трасс, вызываемых са-

мокомпенсацией их температурных

удлинений, реакции опор и подвесок

изменяются пропорционально верти-

кальным температурным перемеще-

ниям Поэтому расчеты трубопроводов

на весовую нагрузку должны выпол-

няться совместно с их расчетами на

самокомпенсацию с учетом податли-

вости опор и подвесок. Такие совме-

стные расчеты сложны и могут выпол-

няться только на ЭВМ по специаль-

ным программам.

Рассмотрим методику упрощенно-

го безмашинного расчета неразветвлен-

ного пространственного трубопрово-

да на весовую нагрузку, разрабо-

танную МЭИ. В этой методике ис-

пользован известный из курсов со-

противления материалов метод сил.

Трасса, подлежащая расчету на ве-

совую нагрузку, обычно имеет на обо-

их концах А и Б жесткое закрепление

и нагружена направленной вниз рав-

номерно распределенной весовой на-

грузкой q, Н/м, включающей вес ме-

талла трубопровода и его тепловой

изоляции. Иногда дополнительно учи-

тывается вес заполняющей трубопро-

вод среды. В промежуточных точках

к трубопроводу приложены сосредо-

точенные силы — реакции опор и под-

весок, обычно направленные вверх.

В этом виде трасса представляет со-

бой для расчета шестикратно статиче-

ски неопределимую систему. Неиз-

вестными в ней являются три состав-

ляющих реакции по направлениям ко-

ординатных осей прямоугольной ор-

тогональной системы и три состав-

ляющих реактивных момента в трех

ортогональных

плоскостях

одной

из неподвижных концевых опор (на-

пример, в опоре Б). До начала рас-

чета такой пространственной трассы

на весовую нагрузку ее можно пре-

образовать и, приняв некоторые до-

пущения, привести задачу к трех-

кратно статически неопределимой си-

стеме. Это преобразование расчетной

трассы показано на рис. 6.4. Дуговые

элементы трассы (гибы) условно за-

меняются жесткими прямыми углами.

Наклонные относительно координат-

ных осей участки условно заменяют-

ся парами участков, ориентированных

вдоль координатных осей прямоуголь-

ной системы координат. Далее трас-

са проецируется на горизонтальную

плоскость, чтобы избавиться от вер-

тикальных участков. Действие верти-

кальных участков на трассу заменя-

ется действием сосредоточенных сил,

включающих как собственный вес вер-

тикальных участков, так и приложен-

ные к ним реакции соответствующих

опор и подвесок, имеющихся на вер-

тикальных участках.

Возможность такого преобразова-

ния реальной пространственной трас-

сы в расчетную плоскую оправдыва-

ется тем, что вертикальные участки не

добавляют в трассу новых изгибаю-

щих и крутящих моментов от весовой

нагрузки, а выполняют лишь функцию

передатчиков весовых моментов от

одного горизонтального участка к

другому. По оценке все эти допуще-

ния вносят в данную методику расче-

та моментов и напряжений от ве-

совой нагрузки погрешность не бо-

лее 10 °о.

Дополнительное упрощение рас-

четов неразветвленной трассы на ве-

совую нагрузку достигается приня-

тием равными нулю обеих горизон-

тальных составляющих реакций край-

них неподвижных опор. Приравни-

ваются нулю и моменты в крайних не-

подвижных опорах, действующие в го-

ризонтальной

плоскости.

В результате решение задачи сво-

дится к определению трех неизвест-

ных: вертикальной реакции

реактивных моментов

в ус-

ловно раскрепляемой неподвижной

опоре Б, действующих в вертикаль-

ных плоскостях проекций.

На рис. 6.4, а изображена про-

странственная трасса трубопровода,

подлежащая расчету на весовую на-

грузку. Через 1а,

16,

1в, 2а,

...

обозначены ее промежуточные опоры.

В данной трассе имеется только один

вертикальный участок высотой

На рис. 6.4, б изображена эквива-

лентная плоская трасса, у которой

влияние отброшенного вертикально-

го участка заменено его весом

который вычитается из направленной

вверх реакции

S36.

имевшейся на

вертикальном участке опоры. Реакции

остальных промежуточных опор обо-

значены через

1а

, S

...

На рис. 6.4, в показана оконча-

тельная расчетная плоская схема трас-

сы для весовой нагрузки. Здесь ре-

акция

5зб

—

Расчетная

схема состоит из чередующихся по

направлениям участков, ориентиро-

ванных вдоль горизонтальных осей

X и Z. Начало координат совмещено

с левым концом грассы, а нумерация

участков и их элементов начинается

с правого условно раскрепляемого

конца и ведется в сторону начала ко-

ординат в порядке алфавита и воз-

растающих номеров. Координатные

оси располагаются

гак,

чтобы все

нечетные участки были ориентирова-

ны по оси Z, а все четные — по оси

X Ось Y направлена вверх. Направ-

ления действий реакции

и реактив-

ных моментов

условно рас-

крепляемой неподвижной опоре Б,

принятые в качестве положительных,

указаны на рис 6 4, в.

За.

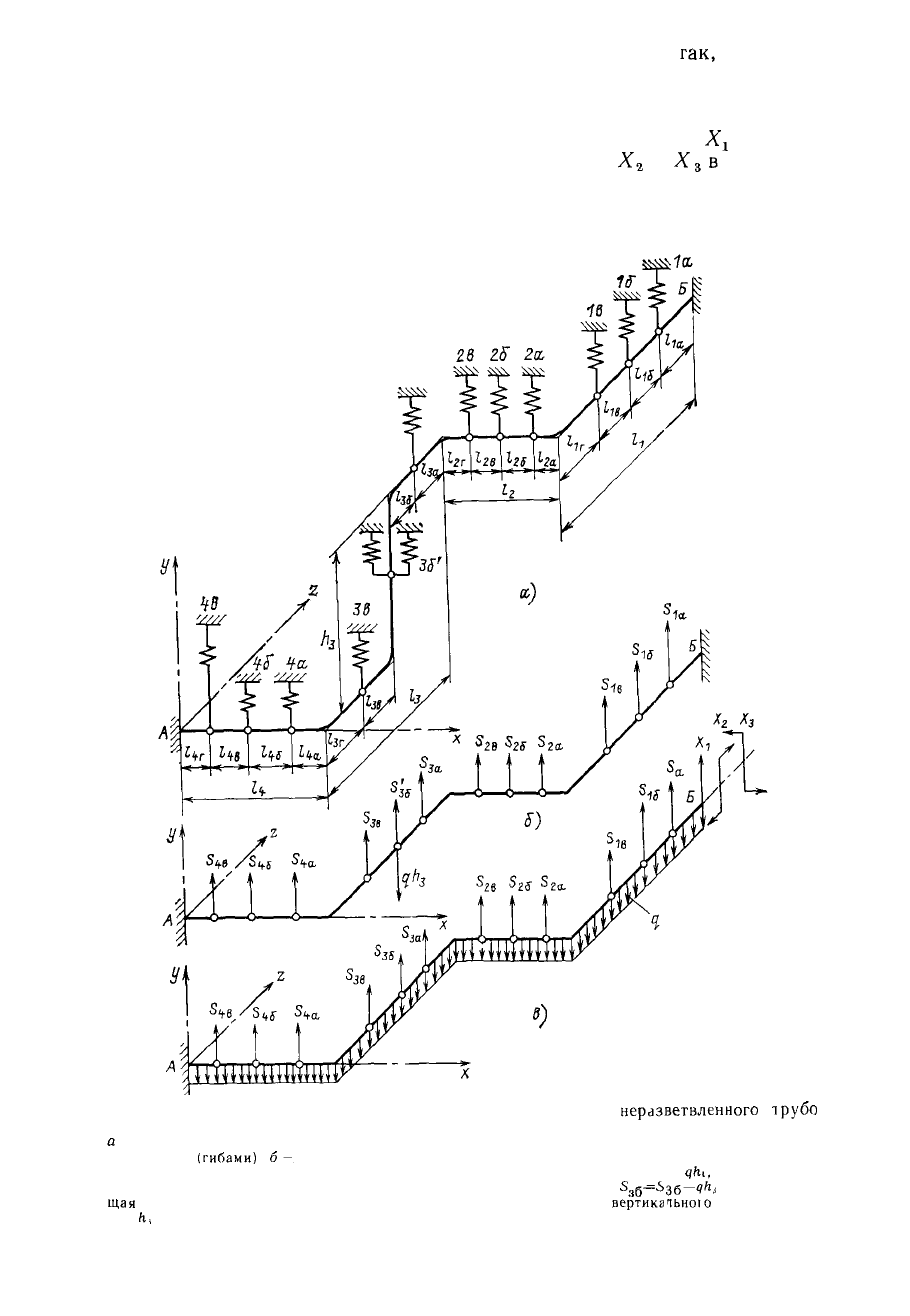
Рис 6 4 Преобразование реальной схемы пространственного

неразветвленного

трубо

провода в расчетную схему для определения моментов от весовой нагрузки

исходная пространственная трасса трубопровода с пружинными подвесками и с дуговыми

элементами

(гибами)

б—

условная плоская схема трассы со спрямленными дуговыми элементами

и с заменой вертикальных участков сосредоточенными весовыми нагрузками

qhi,

в расчетная

плоская схема трассы с окончательным обозначением всех реакций,

^5—636—qh

результирую

щая

расчетная реакция в месте расположения на исходной трассе

вертика

чьною

участка высо

той

Для расчета значений этих реак-

ций служит система канонических

уравнений метода сил:

1р

(6.15)

Физическая сущность этих урав-

нений представляет собой условие ра-

венства нулю вертикального переме-

щения и поворота в двух ортогональ-

ных плоскостях конца трубопровода

в точке расположения условно рас-

крепляемой опоры Б. Для их реше-

ния используется интеграл Мора в

двух его вариантах:

О/г

т=\

dl;

(6.16)

+ •

О/«

= п

'ди

•

)

т= I

dl.

(6.17)

Здесь / = я/64

(d«

—

= 2/ —

экваториальный и полярный моменты

инерции поперечного сечения трубы;

индексом «и» обозначены изгибающие,

а индексом «к» — крутящие моменты;

индекс q присвоен моменту от рас-

пределенной весовой нагрузки

ин-

декс s — моменту от сосредоточенных

реакций

Sty,

M (с чертой наверху)

соответствует моментам от единич-

ных сил или моментов, приложенных

в условно раскрепляемом конце Б

трассы; т — текущий номер элемента

трассы между соседними сосредото-

ченными силами; п — общее число эле-

ментов на всех участках трассы;

—

длина текущего элемента трассы.

Под участком трассы понимается

каждый ее отрезок, параллельный од-

ной из горизонтальных осей коорди-

нат и ограниченный концами участ-

ков другого горизонтального направ-

ления или концами трассы. Каждый

участок разбивается на элементы, гра-

ницами которых являются точки при-

ложения сосредоточенных сил. На-

пример, расчетная схема трассы на

рис. 6.4, в имеет четыре участка, а

каждый участок содержит четыре эле-

мента.

В результате интегрирования по

формуле (6.16) для коэффициентов

получены выражения следующего

вида:

б„=

±L«[A

+ (\ +

v)B

(6.18)

Здесь для

п = 3, для

п = 1, а для

п — 2. Перед выражением для

должен быть знак минус, а

перед остальными — плюс.

за

= 0.

В формуле (6.18)

—

некоторые безразмерные численные ко-

эффициенты, выражающиеся через от-

носительные длины участков, напри-

мер для трассы, состоящей из четырех

участков, один из них имеет вид

4-a

)"^

^-j

, (6.19)

где

l-JL\

/L;

IJL;

, /

— длины уча-

стков; L — общая длина проекции

трассы на горизонтальную плоскость.

Для учета в расчетах расположе-

ния участков относительно направле-

ний координатных осей вводится по-

нятие об их ориентации с присвое-

нием соответствующего знака. При-

нято считать за положительное на-

правление ориентации такое, когда

по пути обхода трассы в направлении

возрастания номеров участков дви-

жение в пределах рассматриваемого

участка происходит против направ-

ления соответствующей координатной

оси. Противоположное направление

считается отрицательным

Например, у трассы, изображен-

ной на рис 6 5, а, отрицательную ори-

ентацию имеет первый участок, а на

рис 6 5,

— второй участок Для

учета ориентации участков в расчет-

ных формулах типа (6 19) выделяются

плечевые члены, знак которых за-

висит от ориентации участка Пле-

чевые сомножители взяты в круглые

скобки и имеют за скобкой верхний

индекс «п» При положительной ори-

ентации участка плечевой сомножи-

тель имеет знак плюс, при отрицатель-

ной — минус Плечевых сомножите-

лей в каждом члене формулы может

быть один или два Некоторые члены

могут вообще не иметь плечевых со-

множителей В таком случае они

всегда положительны Перемножение

плечевых сомножителей в формулах

производится по правилу знаков ал-

гебры

В соответствии с формулой (6 17)

были найдены выражения для сво-

бодных членов

(р

уравнений (6 15):

Д|

±А

±Д

18>

(6.20)

где

= 1, 2, 3. В свою очередь

v)B

(6.21)

а также

4-а,

2в

), (6 22)

где для

т = 4, а для

3, для

п = 3, а для

2Ч

п = 2 Перед выражениями для

должен стоять знак ми-

нус, а перед

— знак

плюс Коэффициенты в формулах

(6 22) в свою очередь определяются

из

выражений вида

a,,

«C

IJfc

(H-v)D

i;S

(6 23)

Здесь по-прежнему

= 1, 2, 3, / —

номер участка; k = а, б, в — обо-

значения сосредоточенных сил в пре-

делах каждого участка Коэффициен-

ты

l}k

lJh

в формулах

(6 21) и (6 23) выражаются через от-

носительные длины участков

оц

и элементов

1а

<х

1б

1в

, а

1г

2а.

<*2б

по особым формулам,

структурно идентичным формуле

(6 19), которые здесь не приводятся.

После того как для заданной трас-

сы с заданными длинами участков и

элементов подсчитаны все

коэффициен

ты по приведенным выше формулам,

не представляет труда выполнить ос-

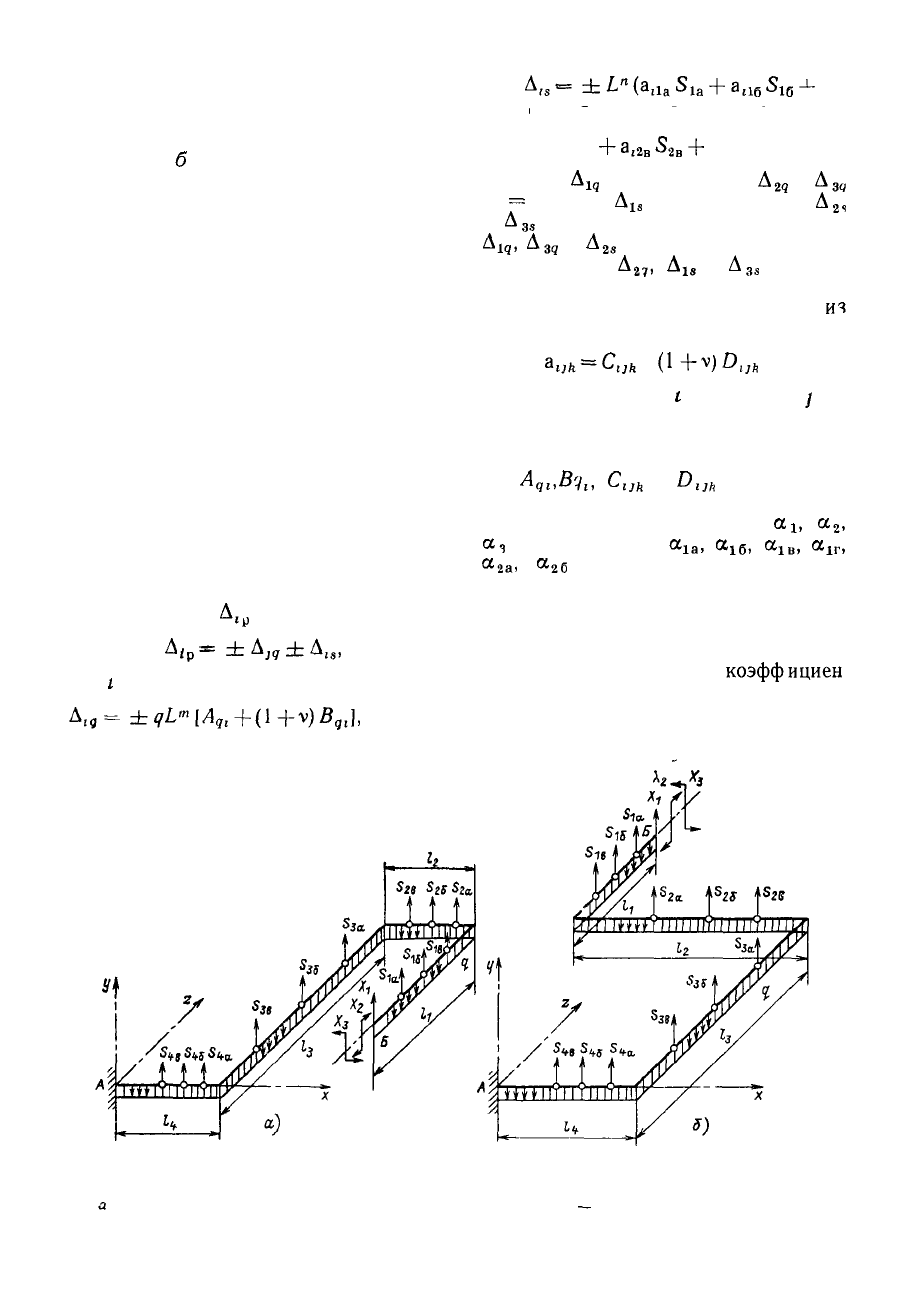
Рис 6 5 Примеры расчетных схем трубопроводных трасс для определения моментов

от весовой нагрузки с отрицательной ориентацией части участков

— трасса с отрицательно ориентированным первым участком б

—

трасса с отрицательно ориен

тированным вторым участком

тальные расчеты и с помощью урав-

нений (6.15) найти неизвестные

для

различных вариантов на-

гружения промежуточных опор. В

этом появляется необходимость при

выборе оптимальной регулировки их

пружин.

Для предварительного выбора зна-

чений реакций промежуточных опор

можно воспользоваться оценочным

способом распределения нагрузки ме-

жду опорами по весам примыкающих

участков трубопровода:

0,5(a

)<7L...

(6.24)

Получающаяся при таком распре-

делении весовой нагрузки между опо-

рами эпюра изгибающих моментов

для трассы не является оптимальной,

однако она в первом приближении

приемлема. Лучшие результаты да-

ет способ определения нагрузок на

опоры в рабочем состоянии трубопро-

вода, базирующийся на уравнениях

строительной механики, которые вы-

ражают условие равенства нулю верти-

кальных перемещений трубопровода

в точках установки опор при совмест-

ном действии весовой и рабочих на-

грузок на опоры. Этот способ назы-

вается способом нулевых перемещений

от весовой нагрузки, но он для реали-

зации требует применения ЭВМ.

Для построения эпюр изгибающих

моментов от весовой нагрузки произ-

водится расчет действующих момен-

тов

п)

элементам каждого участка,

поскольку на стыках элементов пер-

вая производная изгибающих момен-

тов претерпевает разрыв. Расчет про-

изводится раздельно для направления

каждой оси X и Z. Уравнение изги-

бающих моментов для произвольно-

го элемента и участка трассы по оси

Z (аналогично по оси X) может быть

записано следующим образом:

j=^M

—

—0,5qL

(6.25)

Здесь i — номер участка; / — буквен-

ное обозначение элемента в порядке

алфавита;

— изгибающий мо-

мент и поперечная сила в начальном

сечении элемента;

—

zlL

— теку-

щая безразмерная координата; z —

координата текущей точки элемента,

отсчитываемая от начального

сечения.

Расчет эпюр производится последо-

вательно от элемента к элементу, на-

чиная от условно раскрепляемого кон-

ца трассы.

После построения эпюр моментов

определяется опасное сечение, и для

него производится проверка прочно-

сти трубопровода по формулам (6.2)—

(6.13).

На рис. 6.6 в качестве примера

показаны эпюры изгибающих момен-

тов от весовой нагрузки в паро-

проводе, расчетная схема которо-

го состояла из трех участков: первый

и третий ориентированы по оси Z, а

второй — по оси X. Расчет выполнен

как поверочный: реакции промежуточ-

ных опор были предварительно опре-

делены с помощью ЭВМ. Поверочный

безмашинный расчет по описанной вы-

ше методике был выполнен для двух

состояний трассы: холодного (нера-

бочего) и горячего( рабочего). За счет

перемещений трассы при прогреве

значения реакций опор изменялись,

и это было учтено в расчете.

Как видно из рис. 6.6, б, в, при

прогреве трассы и ее температурном

перемещении в результате уменьшения

реакций промежуточных опор реак-

ции неподвижных опор на концах воз-

растают. Это привело к подъему сред-

ней части эпюры и к опусканию ее

краев: изгибающий момент на правом

конце в точке Г меняет при этом знак.

Эпюра моментов у левого края вбли-

зи точки А в рабочем состоянии была

искусственно занижена путем исполь-

зования специальной опоры АТЭП.

6.4. САМОКОМПЕНСАЦИЯ

ТЕМПЕРАТУРНЫХ УДЛИНЕНИЙ

И ТЕМПЕРАТУРНЫЕ ПЕРЕМЕЩЕНИЯ

ТРУБОПРОВОДОВ

Рассмотрим один из наиболее рас-

пространенных методов безмашинно-

го расчета трубопроводов на самоком-

пенсацию температурных

удлинений—

метод упругого центра. При этом

методе не учитываются весовая на-

грузка трубопровода и упругость про-

межуточных опор Метод разработан

лишь для неразветвленных трубопро-

водов. Участок между двумя непод-

вижными опорами можно рассматри-

вать как статически неопределимую

криволинейную балку с жесткими

заделками на концах. Пространствен-

ная неразветвленная трасса при этом

будет шестикратно статически неоп-

ределимой.

Сущность метода упругого центра

сводится к

использованиюдля

раскры-

тия статической неопределимости рас-

четной балки (трубопроводной трас-

сы) теоремы Кастильяно, согласно

которой первая производная потен-

циальной энергии деформации балки

по одной из обобщенных независимых

внешних сил равна обобщенному пе-

ремещению, соответствующему этой

силе в точке ее приложения При

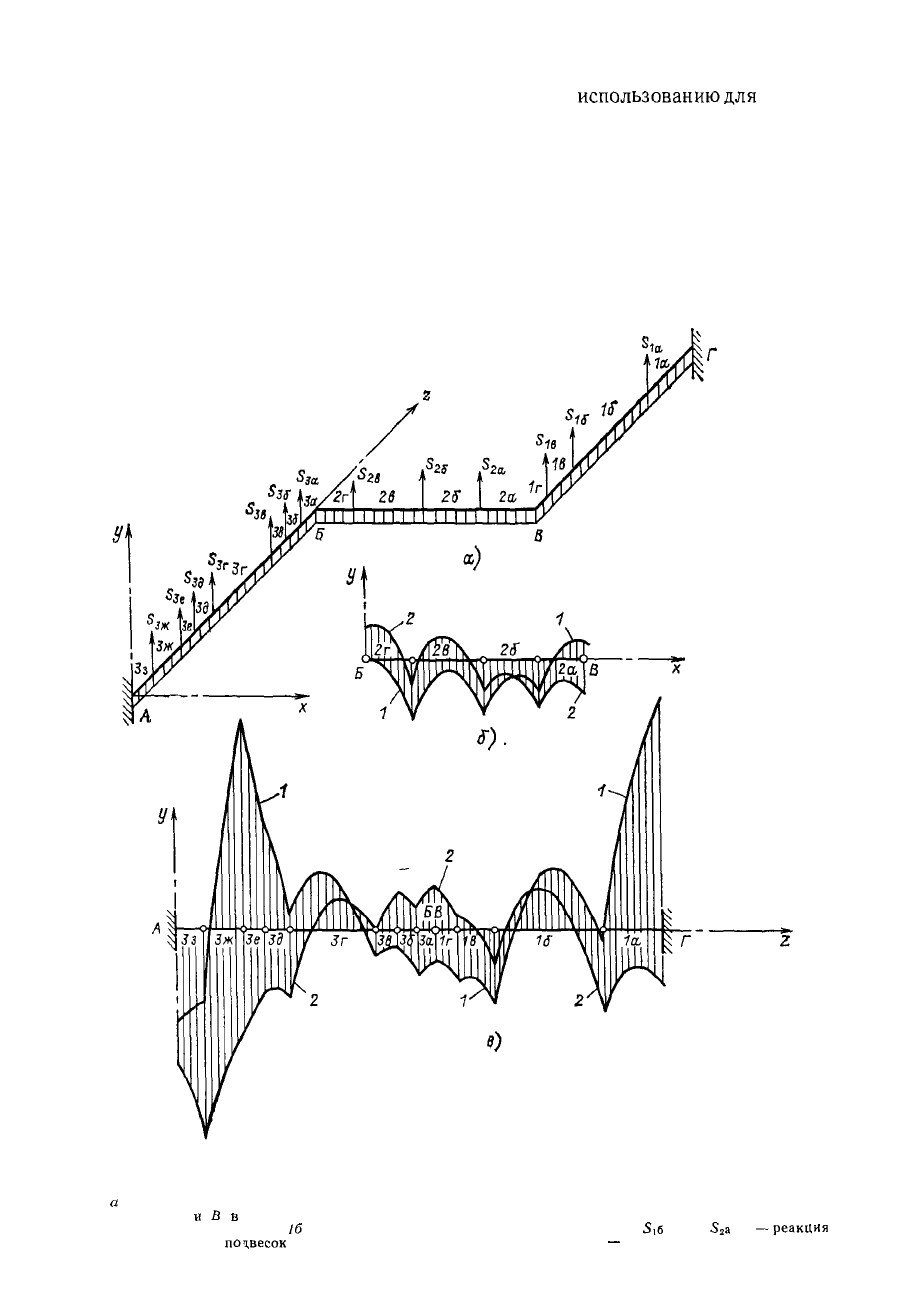
Рис 6 6 Пример эпюр изгибающих моментов от весовой нагрузки в паропроводе све-

жего пара блока Т 250/300-240

— расчетная схема трассы, б — эпюры изгибающих моментов на втором участке трассы между

точками Б

направлении оси X, в — эпюры изгибающих моментов на участках ГВ и БА в

направлении оси Z, 1а,

1в, 1г, 2а — номера элементов трассы, S,a

S,6

S,B,

—реакция

промежуточных

подвесок

и опор, / — холодное состояние трассы, 2 — горячее рабочее состояние

раскрытии статической неопредели-

мости одна из концевых неподвижных

опор условно отбрасывается и ее дей-

ствие заменяется приложенными на

этом конце трассы силами и момен-

тами. В случае пространственной трас-

сы необходимо приложить на конце

три составляющие силы по направле-

ниям координатных осей и три мо-

мента в трех ортогональных плоско-

стях.

При прогреве от монтажной (20

°С)

до рабочей температуры трубопровод

удлиняется, а неподвижные опоры на

концах препятствуют его свободному

удлинению. В результате трубопро-

вод деформируется и при пространст-

венной трассе в нем возникают изги-

бающие и крутящие компенсационные

моменты и соответствующие им напря-

жения.

Потенциальная энергия деформа-

ции трубопровода приближенно равна:

где

— соответственно из-

гибающий и крутящий моменты в

произвольной точке трассы; L —

длина геометрической оси трубопро-

вода между неподвижными опорами.

Поскольку

вторым членом

формулы (6.26) можно пренебречь.

Вывод основных формул расчета

на самокомпенсацию проще сделать

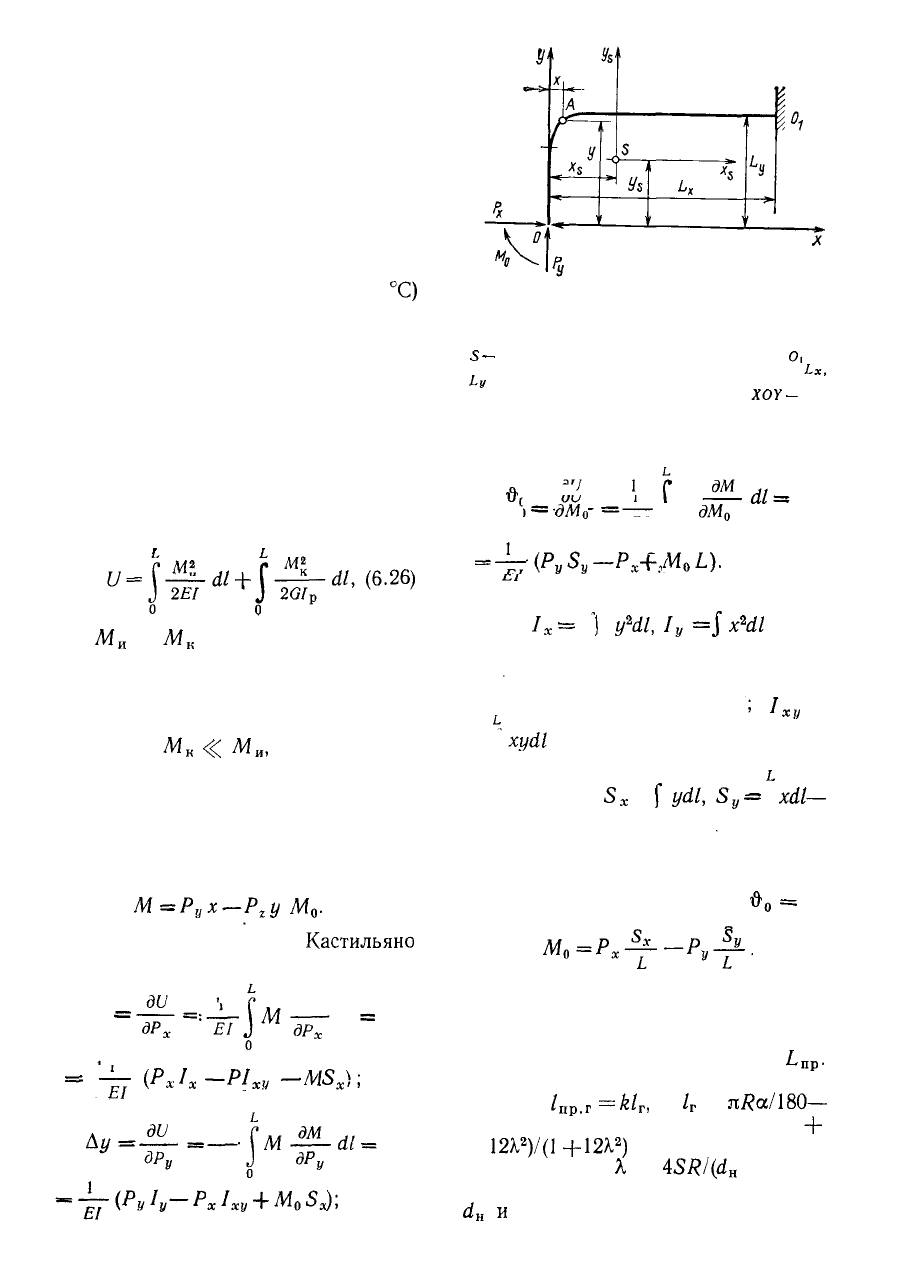
для плоской трассы (рис. 6.7). Изги-

бающий момент в любом сечении А

трубопровода

М=Р„х—Р

(6.27)

Согласно теореме

Кастильяно

обобщенные перемещения

Ах-

:_L-

дМ

-^-

(Р

-Р

„

-М

);

(6.28)

(6.29)

Рис. 6.7. Схема плоского неразветвленного

трубопровода к расчету на самокомпенса-

цию:

— упругий центр тяжести трассы; О и

О,

—

места расположения неподвижных опор;

Lx,

— расстояния между неподвижными опорами

в направлениях координатных осей;

XOY

— ис-

ходная система координат; XsSYa — система

координат, проходящих через упругий центр тя-

жести трассы

,=-^-=— м

дМ

El J

дМ

^-^—(PySy—P

L).

(6.30)

L L

Здесь

)

уЧ1,

1у—

хЧ1

— ли-

b о

нейные моменты инерции геометри-

ческой оси трубопровода относитель-

но координатных осей,

ху

= j

xydl

— центробежный момент

инерции; м

;

ydl,

xdl—

d о

статические моменты геометриче-

ской оси трубопровода относительно

координатных осей.

Для неподвижной опоры

тогда

-^--P

-jf-.

(6.31)

Здесь L — длина геометрической оси

трубопровода. С учетом пониженной

жесткости дуговых элементов трас-

сы берется приведенная длина

Приведенная длина дугового элемен-

та (гиба) /

пр

=kl

где /

nRa/180—

длина дуги с углом a; k = (10

-j-

12Л.

)/(1

12^

)

— коэффициент гиб-

кости Кармана;

4SR/(d

— S)

—

геометрическая характеристика гиба;

S — наружный диаметр и тол-

0,374

0^955

0,93

0,3

105

a,866

120

0,827

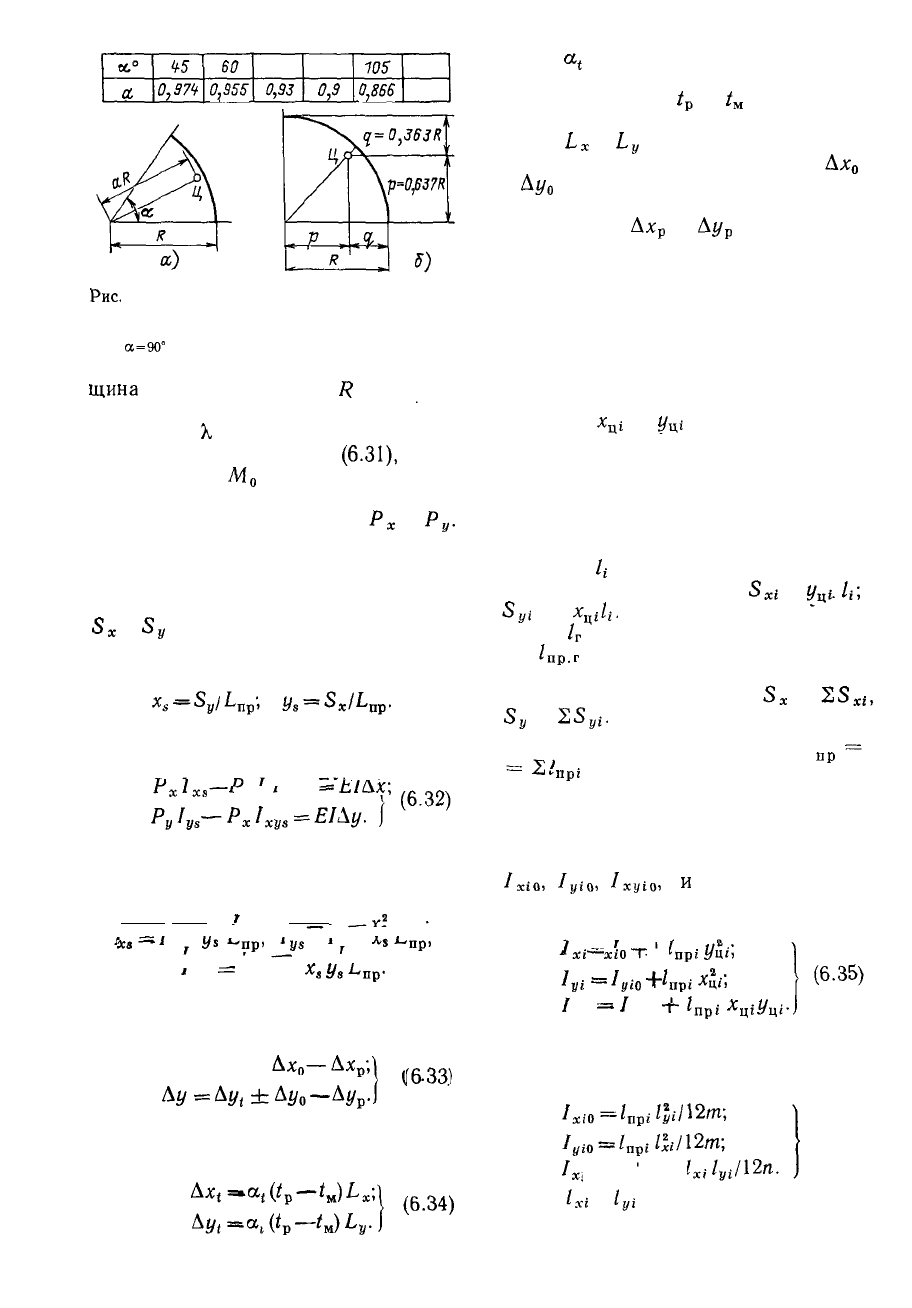
Рис.

6.8. Определение координат центра

тяжести дугового элемента:

а — при произвольной дуге гиба а; б — при дуге

гиба

сх=9О°

щина

стенки трубы, м;

— радиус

гиба, м. Формула Кармана справед-

лива при

> 0,3.

Пользуясь выражением

(6.31),

мож-

но исключить

из уравнений (6.28)

и (6.29). Получается система из двух

уравнений для определения

Для дальнейшего упрощения решения

переносят оси координат в упругий

центр тяжести (УЦТ) рассматривае-

мой трассы: ее статические моменты

относительно новых осей ко-

ординат равны нулю. Координаты

УЦТ определяют по формулам

В результате система уравнений

приобретает вид

'x'xs

xys ^El&X,

-P

xys

^EIAy.

Для переноса координатных осей

в упругий центр тяжести используют

формулы

Т Т „2

, I I

i/s

*-пр>

'у$

^пр>

xys

* ху

»Уа'"П'р-

Входящие в формулы (6.32) рас-

четные линейные перемещения конца

0 участка определяют по формулам

Ах = Ах, ± Ал:

—

Ах

Аг/=Д£/

(

±Аг/

—Аг/

Температурные удлинения уча-

стка по направлениям координатных

осей

Ax<—о,

(*„—*„)

Здесь

— температурный коэффи-

циент линейного расширения матери-

ала трубопровода;

— рабочая

и монтажная температуры трубопро-

вода;

— расстояния между

неподвижными опорами участка;

Ах

Ау

— заданные перемещения кон-

цов рассматриваемого расчетного уча-

стка трассы;

Ах

Ау

— значения

предварительной растяжки трубопро-

вода.

Наибольшую трудоемкость по этой

методике расчета представляет опре-

деление моментов инерции и стати-

ческих моментов трассы. Для этого

трассу разбивают на прямолинейные

и дуговые элементы и определяют ко-

ординаты

ЦГ

;

центров тяжести

каждого из них. Для прямолинейных

элементов они расположены посреди-

не каждого, для дуговых определяют-

ся в соответствии с рис. 6.8. Стати-

ческие моменты прямолинейных эле-

ментов определяют как произведения

их длины

на соответствующие коор-

динаты центров тяжести:

г/

;

Syi

Хц,/,.

Для дуговых элементов

вместо

принимают приведенную дли-

ну

р.г

элемента. Статические мо-

менты всей трассы определяют сум-

мированием по элементам:

1,S

Одновременно вычисляют

приведенную длину трассы: L

^ '

прг

•

Моменты инерции элементов полу-

чают как сумму собственного момента

инерции элемента относительно осей,

проходящих через его центр тяжести,

Ixio,

lyia,

lxyio<

дополнительного

члена, учитывающего перенос осей в

начало координат трассы:

'xi

xiO~T-

'npi

Учи

Iyl-IyiO

laviXb;

xyi

xyio

"•"

'прг

^ЦГ

УЦГ

Собственные моменты инерции

прямых и дуговых элементов здесь

определяются по формулам

(6.36)

Здесь

lyi

— длины проекций эле-

мента на оси X и Y соответственно.

Знаки у собственных линейных мо-

ментов инерции элементов

yi0

всегда положительны. Знак у

центробежного момента инерции

xyi0

зависит от положения прямолинейно-

го элемента и хорды дугового элемен-

та относительно положительных на-

правлений координатных осей

(рис. 6.9): если луч, проведенный че-

рез начало координат параллельно

прямому отрезку или хорде дуги,

проходит в первом и третьем квад-

рантах, то знак момента инерции по-

ложительный, если во втором и чет-

вертом — отрицательный.

Для прямолинейных элементов

т = п = 1, для дуговых

тип

при-

нимают в зависимости от угла

дуги

а :

а . . .30° 45° 60° 75° 90° 105°

т .... 1 0,98 0,96 0,93 0,88 0,83

л .... 1 0,99 0,98 0,97 0,96 0,95

Решая совместно уравнения (6.32),

можно определить реакции

Если эти реакции перенести в упругий

центр трассы S, как показано на

рис. 6.10, то изгибающий момент в

любой точке, например Б, трассы мо-

жет быть определен как произведе-

ние равнодействующей Р =

УР\

Р\

на длину перпендикуляра

MR,

опущенного на ее направление тп

из рассматриваемой точки Б. Таким

образом, отрезок

(длина опущен-

ного перпендикуляра) в определенном

масштабе представляет значение из-

гибающего момента в произвольной

точке трассы (на рис. 6.10 штрихов-

кой показана эпюра изгибающих мо-

ментов). Знак момента по длине трас-

сы изменяется. В точках пересече-

ния геометрической оси трассы с ли-

нией тп изгибающие моменты равны

нулю.

При расчетах на самокомпенсацию

пространственных трасс вводится по-

нятие статических моментов S и

моментов инерции / относительно

плоскостей проекций. По аналогии с

формулой (6.35) моменты инерции

элементов относительно координатных

плоскостей определяют суммирова-

нием собственных моментов инерции

относительно плоскостей, проходящих

квадрант

II квадрант

т'

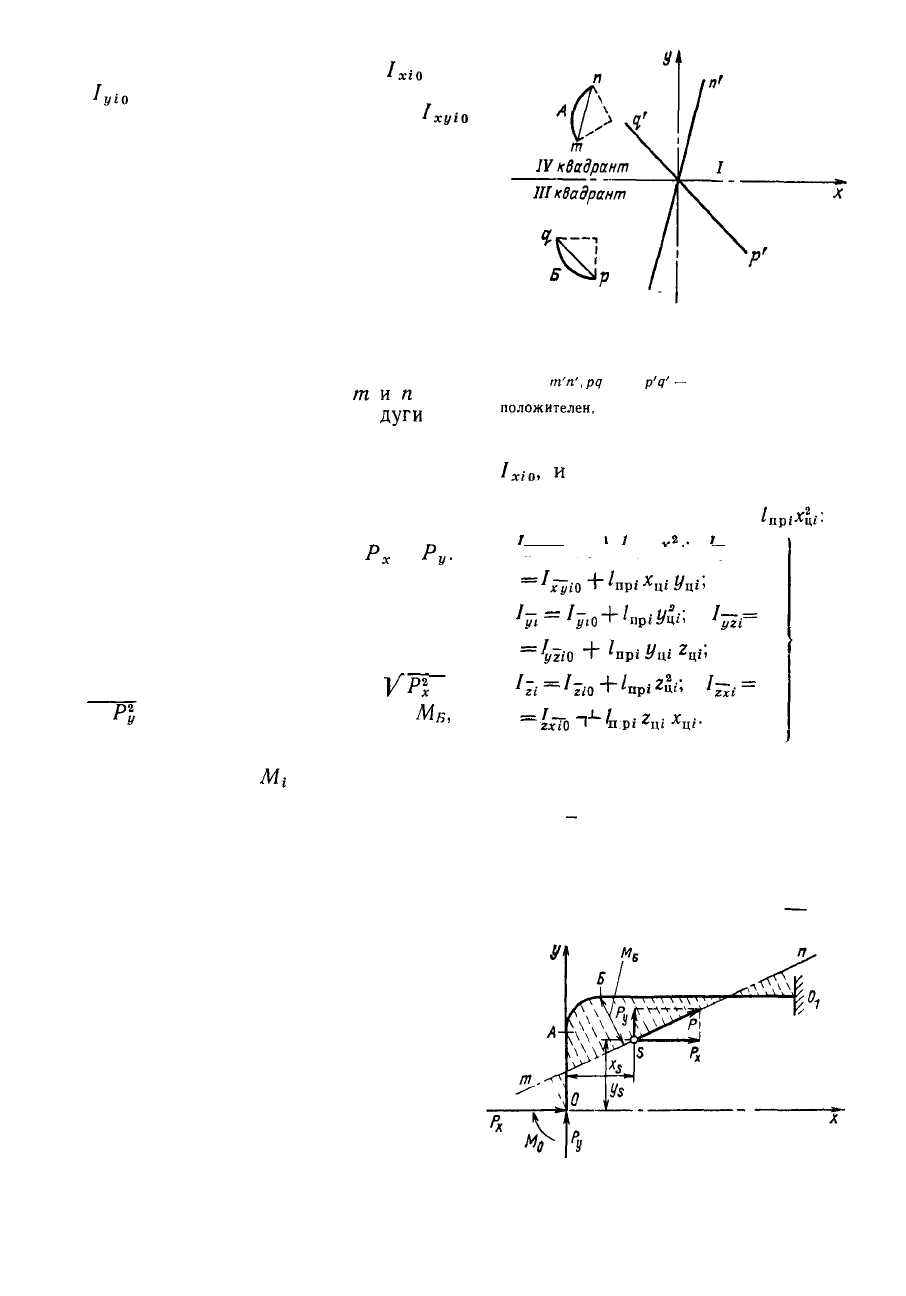
Рис. 6.9. К определению знака у центро-

бежного момента инерции дугового или

наклонного прямолинейного элемента:

тп и

т'п\

рц

р'?'—

взаимно параллельные

линии; центробежный момент инерции дуги А

положителен,

а дуги В отрицателен

через их центры тяжести, например

/же.

дополнительных членов, учи-

тывающих перенос осей в начало ко-

ординат трассы, например

v.2..

Iy,0

УцЬ

Уц1'<

Ijii

(6.37)

yziO

"Г"

'npi

УЦГ

цЬ

zxiO

"•

Здесь моменты инерции относительно

плоскостей проекций обозначены ин-

дексами с чертой наверху. Например,

через х обозначена плоскость, пер-

пендикулярная оси X. Центробежные

моменты инерции относительно двух

плоскостей обозначены двойными ин-

дексами с чертой, например ху. Соб-

Рис. 6.10. Эпюра изгибающих компенсаци-

онных моментов в паропроводной трассе,

изображенной на рис. 6.7