Richards J.A., Jia X. Remote Sensing Digital Image Analysis: An Introduction

Подождите немного. Документ загружается.

1.4 Spatial Data Sources in General 19

Table 1.2. Some GIS data manipulation operations

used (see Sect. 4.2); however as geometric detail is not preserved in a histogram

this is rarely a suitable code for an image on its own. One effective possibility that

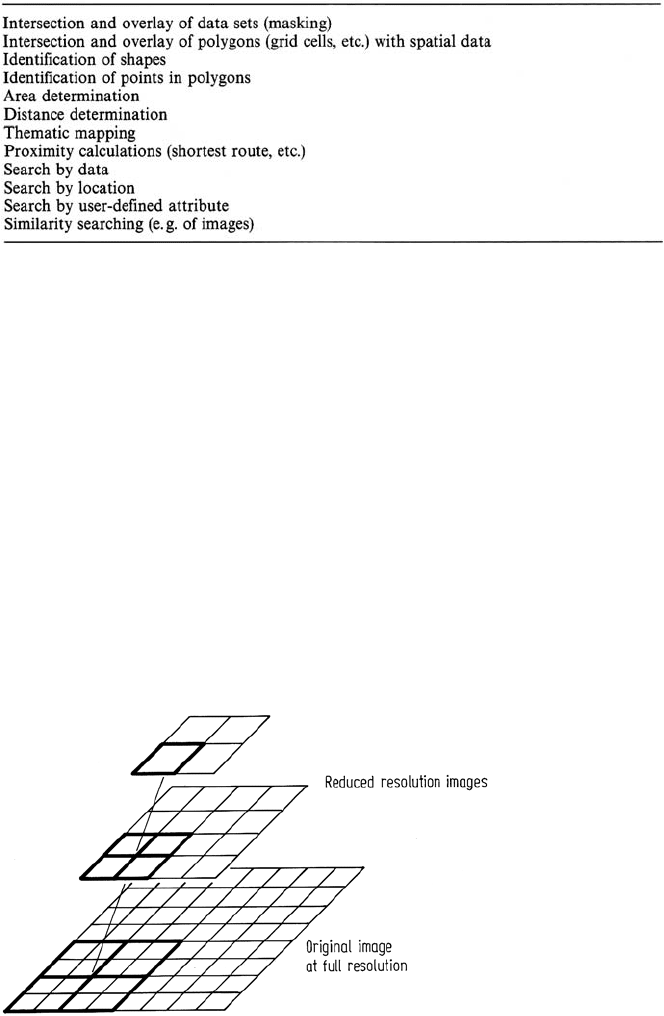
has been explored is the use of image pyramids. A pyramid is created by combining

groups of pixels in a neighbourhood to produce a new composite pixel of reduced

resolution, and thus a low resolution image with fewer pixels. This process is repeated

on the processed image to form a new image of lower resolution (and fewer pixels)

still. Ultimately the image could be reduced to one single pixel that is a global

measure of the image’s brightness. Since pixels are combined in neighbourhood

groups, spatial detail is propagated up through the pyramid, albeit at decreasing

resolution. Figure 1.14 illustrates how an image pyramid is constructed by simple

averaging of non-overlapping sets of 2 × 2 pixels. It is a relatively easy matter

(see Problem 1.6) to show that the additional memory required to store a complete

pyramid, constructed as in the ﬁgure, is only 33% more than that required to store

just the image itself.

Fig. 1.14. Construction of an image pyramid by successively averaging groups of 2 ×2 pixels

20 1 Sources and Characteristics of Remote Sensing Image Data

Having developed an image pyramid, signatures that can be used to undertake

similarity searching include the histograms computed over rows and columns in the

uppermost levels of the pyramid (see Problem 1.7). A little thought shows that this

allows an enormous number of images to be addressed, particularly if each pixel is

represented by an 8 bit brightness value.As a result very fast searching can be carried

out on these reduced representations of images.

Image pyramids are discussed by Rosenfeld (1982) and have been considered in

the light of image similarity searching by Chien (1980), and data mining by Datcu

et al. (2003).

There is sometimes an image processing advantage to be obtained when using a

pyramid representation of an image. In edge detection, for example, it is possible to

localise edges quickly, without having to search every pixel of an image, by ﬁnding

apparent edges (regions) in the upper levels of the pyramid. The succeeding lower

pixel groupings are then searched to localise the edges better.

Finally the pyramid representation of an image is felt to have some relation

to human perception of images. The upper levels contain global features and are

therefore not unlike the picture we have when ﬁrst looking at a scene – generally

we take the scene in initially “as a whole" and either miss or ignore detail. Then

we focus on regions of interest for which we pay attention to detail because of the

information it provides us with.

1.4.4

The Challenge to Image Processing and Analysis

Much of the experience gained with digital image processing and analysis in remote

sensing has been with multispectral image data. In principle however any spatial data

type in digital format can be processed using the techniques and procedures presented

in this book. Information extraction from geophysical data could be facilitated, for

example, if a degree of sharpening is applied prior to photointerpretation, while

colour density slicing could assist the interpretation of topography. However the real

challenge to the image analyst arises when data of mixed types are to be processed

together. Several issues warrant comment.

The ﬁrst relates to differences in resolution, an issue that arises also when treating

multi-source satellite data such as Landsat ETM+ and Aqua MODIS. The analyst

must decide, for example what common pixel size will be used when co-registering

the data, since either resolution or coverage will normally be sacriﬁced. Clearly this

decision will be based on the needs of a particular application and is a challenge

more to the analyst than the algorithms.

The more important consideration however is in relation to techniques for ma-

chine assisted interpretation. There is little doubt that combined multispectral and,

say, topographic or land ownership maps can yield more precise thematic (i.e. cat-

egory of land cover, etc.) information for a particular region than the multispectral

data on its own. Indeed the combination of these sources is often employed in pho-

tointerpretive studies.

1.5 A Comparison of Scales in Digital Image Data 21

The issue is complicated further when it is recalled that much of the non-spectral,

spatial data available is not in numerical point form but rather is in nominal area or

line format. With these, image analysis algorithms developed algebraically will not be

suitable. Rather same degree of logical processing of labels combined with algebraic

processing of arithmetic values (such as pixel brightnesses) is necessary.

Chapter 12 addresses this issue by considering several numerical and knowledge-

based image analysis methods, which lend themselves to handling both numerical

and non-numerical data sources.

1.5

A Comparison of Scales in Digital Image Data

Because of IFOV differences the digital images provided by various remote sensing

sensors will ﬁnd application at different scales. As a guide Table 1.3 relates scale

to spatial resolution; this has been derived somewhat simplistically by considering

an image pixel to be too coarse if it approaches 0.1 mm in size on a photographic

product at a given scale. Thus Landsat MSS data is suggested as being suitable for

scales smaller than about 1 : 500,000 whereas NOAA AVHRR data is suitable for

scales below 1 : 10,000,000. Detailed discussions of image quality in relation to scale

will be found in Welch (1982), Forster (1985), Woodcock and Strahler (1987) and

Light (1990).

Table 1.3. Suggested maximum scales of photographic products as a function of effective

ground pixel size (based on 0.1 mm printed pixel)

Scale Approx. Pixel Size (m) Sensor (nominal)

1 : 10,000 1 Ikonos panchromatic

1 : 50,000 5 aircraft MSS, Ikonos XS

1 : 100,000 10 Spot HRG

1 : 250,000 25 Spot HRVIR, Landsat TM

1 : 500,000 50 Landsat TM, LISS

1 : 5,000,000 500 OCTS, OCM

1 : 10,000,000 1000 NOAA AVHRR, MODIS

1 : 50,000,000 5000 GMS thermal IR band

22 1 Sources and Characteristics of Remote Sensing Image Data

References for Chapter 1

More details on satellite programs, along with information on sensors and data characteristics

can be found in the web sites of the responsible agencies. Some of particular use are:

For weather satellites

http://www.wmo.ch

http://www.ncdc.noaa.gov

http://www.eumetsat.de

For earth observation satellites

http://www.nasa.gov

http://www.orbimage.com

http://hdsn.eoc.nasda.go.jp

http://www.spotimage.fr

http://www.spaceimaging.com

http://earth.esa.int

http://www.isro.org

For radar missions

http://www.rsi.ca

http://southport.jpl.nasa.gov

For imaging spectrameters

http://www.techexpo.com/WWW/opto-knowledge/

The Manual of Remote Sensing (1999) provides an excellent and comprehensive coverage of

the ﬁeld of remote sensing, and spectral reﬂectance characteristics in particular.

Cloude et al. (1998) gives a contemporary account of interferometric synthetic aperture radar

and its application to topograhic mapping.

R. Bolstad, 2002: GIS Fundamentals: A First Text on Geographical Information Systems,

Eider.

M.T. Chahine, 1983: Interaction Mechanisms within the Atmosphere. In Manual of Remote

Sensing, R.N. Colwell (Ed). 2e. American Society of Photogrammetry, Falls Church, Va.

Y.T. Chien, 1980: Hierarchical Data Structures for Picture Storage, Retrieval and Classiﬁcation.

In Pictorial Informations Systems, S.K. Chang and K.S. Fu (Eds.), Springer-Verlag, Berlin.

S.R. Cloude and K.P. Papathanassiou, 1998: Polarimetric SAR Interferometry. IEEE Trans.

Geoscience and Remote Sensing, 36, 1551–1565.

M. Datcu, H. Daschiel, A. Pelizzari, M. Quartulli, A. Galoppo, A. Colapicchioni, M. Pastori,

K. Seidel, P. Marchetti and S. D’Elia, 2003: Information Mining in Remote Sensing Image

Archives. IEEE Trans. Geoscience and Remote Sensing, 41, 2923–2936.

C. Elachi (Chairman), 1983: Spaceborne Imaging Radar Symposium. Jet Propulsion Labora-

tory, January 17–20. JPL Publication 83–11.

C. Elachi, T. Bicknell, R.L. Jordan and C. Wu, 1982: Spaceborne Synthetic Aperture Imaging

Radars. Applications, Techniques and Technology. Proc. IEEE, 70, 1174–1209.

Problems 23

C. Elachi, 1988: Spaceborne Radar Remote Sensing:Applications and Techniques. N.Y., IEEE.

B.C. Forster, 1985: Mapping Potential of Future Spaceborne Remote Sensing Systems. Insti-

tution of Surveyors (Australia) Annual Congress, Alice Springs.

R.M. Hoffer, 1978: Biological and Physical Considerations in Applying Computer-Aided

Analysis Techniques to Remote Sensor Data. In P.H. Swain and S.M. Davis, Eds., Remote

Sensing: The Quantitative Approach, N.Y., McGraw-Hill.

D.L. Light, 1990: Characteristics of Remote Sensors for Mapping and Earth Science Appli-

cations. Photogrammetric Engineering and Remote Sensing, 56, 1613–1623.

Manual of Remote Sensing, Remote Sensing for the Earth Sciences, 1999. A.N. Renez and

R.A Ryerson (Eds.), 3rd ed., NY, Wiley.

A. Rosenfeld, 1982: Quadtrees and Pyramids: Hierarchical Representation of Images, Report

TR-1171, Computer Vision Laboratory, University of Maryland.

K. Tomiyasu, 1978: Tutorial Review of Synthetic-Aperture Radar (SAR) with Applications to

Imaging of the Ocean Surface. Proc. IEEE, 66, 563–583.

R. Welch, 1982: Image Quality Requirements for Mapping from Satellite Data. Proc. Int.

Soc. Photogrammetry and Remote Sensing, Commission 1. Primary Data Acquisition,

Canberra.

F.T. Ulaby, R.K. Moore and A.K. Fung, 1981, 1982, 1985: Microwave Remote Sensing, Active

and Passive. Vols. 1,2,3 Reading Mass. Addison-Wesley.

C.E. Woodcock and A.H. Strahler, 1987: The Factor of Scale in Remote Sensing. Remote

Sensing of Environment, 21, 311–332.

H.A. Zebker and R.M. Goldstein, 1986: Topogaphic Mapping from Interferometric Synthetic

Aperture Radar Observations. J. Geophysical Research, 91, 4993–4999.

Problems

1.1 Plot graphs of pixel size in equivalent ground metres as a function of angle from nadir

across a swath for

a) Landsat MSS with IFOV of 0.086 mrad, FOV = 11.56

◦

b) NOAA AVHRR with IFOV = 1.3 mrad, FOV = 2700 km, altitude = 833 km,

c) an aircraft scanner with IFOV = 2.5 mrad, FOV = 80

◦

ﬂying at 1000 m AGL (above ground

level),

producing separate graphs for the along track and across track dimensions of the pixel. Replot

the graphs to indicate pixel size relative to that at nadir.

1.2 Imagine you have available image data from a multispectral scanner that has two narrow

spectral bands. One is centred on 0.65 µm and the other on 1.0 µm wavelength. Suppose the

corresponding region on the earth’s surface consists of water, vegetation and soil.

Construct a graph with two axes, one representing the brightness of a pixel in the 0.65 µm

band and the other representing the brightness of the pixel in the 1.0 µm band. In this show

where you would expect to ﬁnd vegetation pixels, soil pixels and water pixels. Note how

straight lines could, in principle, be drawn between the three groups of pixels so that if a

computer had the equations of these lines stored in its memory it could use them to identify

every pixel in the image.

Repeat the exercise for a scanner with bands centred on 0.95 µm and 1.05 µm.

1.3 There are 460 185 km × 185 km frames of Landsat data that cover Australia. Compute

the daily data rate (in Gbit/day) for Australia provided by the ETM+ sensor on Landsat 7,

assuming all possible scenes are recorded.

24 1 Sources and Characteristics of Remote Sensing Image Data

1.4 Assume a “frame" of image data consists of a segment along the track of the satellite,

as long as the swath is wide. Compute the data volume of a single frame from each of the

following sensors and produce a graph of average data volume per wavelength band versus

pixel size.

NOAA AVHRR

Aqua MODIS

ADEOS AVNIR (multispectral)

Landsat ETM+

Spot HRG (multispectral)

1.5 Determine a relationship between swath width and orbital repeat cycle for a polar orbiting

satellite at an attitude of 800 km, assuming that adjacent swaths overlap by 10% at the equator.

1.6 An image pyramid is to be constructed in the following manner: Groups of 2 × 2 pixels

are averaged to form single pixels and thereby reduce the number of pixels in the image by

a factor of 4, while reducing its resolution as well. Groups of 2 × 2 pixels in the reduced

resolution image are then averaged to form a third version of lower resolution still. This

process can be continued until the original image is represented by a pyramid of progressively

lower resolution images with a single pixel at the top.

Determine the additional memory required to store the complete pyramid by comparison

to storing just the image itself. (Hint: Use the properties of a geometric progression.)

Repeat the exercise for the case of a pyramid built by averaging 3 ×3 groups of pixels.

1.7 A particular image data base is to be constructed to allow similarity searching to be

performed on sets of binary images i.e. on images in which pixels take on brightness values

of 0 or 1 only. Image pyramids are to be stored in the data base where each succeeding higher

level in a pyramid has pixels derived from 3 × 3 groups in the immediately lower level. The

value of the pixel in the higher level is to be that of the majority of pixels in the corresponding

lower group. The uppermost level in the pyramid is a 3 × 3 image.

(i) How much additional storage is required to store the pyramids rather than just the

original images?

(ii) The search algorithm to be implemented on the top level of the pyramid is to consist

of histogram comparison. In this histograms are taken of the pixels along each row and

down each column and a pair of images are ‘matched’ when all of these histograms

are the same for both images. In principle, how many distinct images can be addressed

using the top level only?

(iii) An alternative search algorithm to that mentioned in (ii) is to compute just the simple

histogram of all the pixels in the top level of the pyramid. How many distinct images

could be addressed in this case using the top level only?

(iv) Would you recommend storing the complete pyramid for each image or just the original

image plus histogram information for the upper levels of a pyramid?

(v) An alternative means by which the upper levels of the pyramid could be coded is simply

by counting and storing the fraction of 1’s which occurs in each of the ﬁrst few upper-

most levels. Suppose this is done for the top three levels. Show how a feature or pattern

space could be constructed for the complete image data base, using the 1’s fractions for

the upper levels in each image, which can then be analysed and searched using pattern

classiﬁcation procedures.

1.8 A particular satellite carries a high resolution optical sensor with 1 m spatial resolution

and is at 800 km altitude in a near polar orbit. Orbital period is related to orbital radius by:

Problems 25

T = 2π



where µ = 3.986 × 10

−2

, and orbital radius is given by

r = a + h

in which a = 6.378 Mm and h is altitude.

If the orbit is arranged such that complete earth coverage is possible, how long will that

take if there are 2048 pixels per swath? Consequently, what sorts of applications would such

a satellite be used for?

1.9 Suppose a particular sensor recorded reﬂectance data in just two wavebands. Further,

suppose its radiometric resolution were only 2 bits – i.e. are just four levels of grey available

in each of the two bands. What is the theoretical maximum number of different cover types

that could be discriminated with the sensor – i.e. how many different unique brightness value-

waveband pairs are available? Those pairs are in fact the individually resolvable sites in the

coordinate space discussed in problem 1.2.

Show that if a sensor has c channels and a radiometric resolution of b bits that the total

number of sites in the space is 2

. How many different sites are there for the following

sensors?

Spot HRV

Landsat Thematic Mapper

OrbView2 SeaWiFS

Aqua MODIS

EO-1 Hyperion.

For an image of 512 ×512 pixels how many sites, on the average, will be occupied for each

of the sensors above?

Error Correction

and Registration of Image Data

When image data is recorded by sensors on satellites and aircraft it can contain

errors in geometry and in the measured brightness values of the pixels. The latter

are referred to as radiometric errors and can result from the instrumentation used

to record the data, from the wavelength dependence of solar radiation and from the

effect of the atmosphere. Image geometry errors can arise in many ways. The relative

motions of the platform, its scanners and the earth, for example, can lead to errors

of a skewing nature in an image product. Non-idealities in the sensors themselves,

the curvature of the earth and uncontrolled variations in the position and attitude of

the remote sensing platform can all lead to geometric errors of varying degrees of

severity.

When an image is to be utilized it is frequently necessary to make corrections

in brightness and geometry if the accuracy of interpretation, either manually or by

machine, is not to be prejudiced. For many applications only the major sources of

error will require compensation whereas in others more precise correction will be

necessary.

It is the purpose of this chapter to discuss the nature of the radiometric and

geometric errors commonly encountered in remote sensing images and to develop

computational procedures that are used for their compensation. While this is the

principal intention, the procedures to be presented ﬁnd more general application

as well, such as in registering together sets of images of the same region but at

different times, and in performing operations such as scale changing and zooming

(magniﬁcation).

Radiometric correction procedures for hyperspectral imagery are treated sepa-

rately in Chap. 13.

2.1

Sources of Radiometric Distortion

Mechanisms that affect the measured brightness values of the pixels in an image can

lead to two broad types of radiometric distortion. First, the relative distribution of

28 2 Error Correction and Registration of Image Data

brightness over an image in a given band can be different to that in the ground scene.

Secondly, the relative brightness of a single pixel from band to band can be distorted

compared with the spectral reﬂectance character of the corresponding region on the

ground. Both types can result from the presence of the atmosphere as a transmission

medium through which radiation must travel from its source to the sensors, and can

be a result also of instrumentation effects.

2.1.1

The Effect of the Atmosphere on Radiation

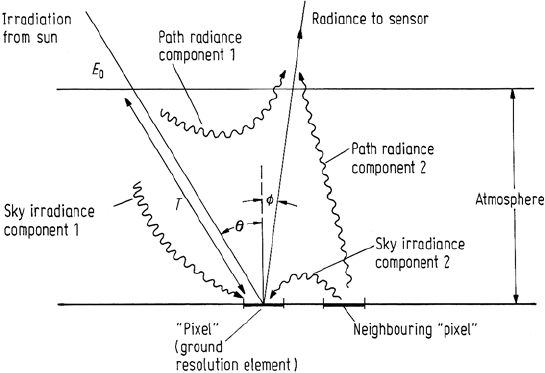
Figure 2.1 depicts the effect the atmosphere has on the measured brightness value

of a single pixel for a passive remote sensing system in which the sun is the source

of energy, as in the visible and reﬂective infrared regions. In the absence of an

atmosphere the signal measured by the sensor will be a function simply of the level

of energy from the sun, actually incident on the pixel, and the reﬂectance properties

of the pixel itself. However the presence of the atmosphere can modify the situation

signiﬁcantly as depicted in the diagram. Before discussing this in detail it is of value

to introduce some deﬁnitions of radiometric quantities as these will serve to simplify

explanations and will allow correction equations to be properly formulated.

Imagine the sun as a source of energy emitting at a given rate of Joules per second,

or Watts. This energy radiates through space isotropically in an inverse square law

fashion so that at a given distance the sun’s emission can be measured as Watts per

square metre (given as the power emitted divided by the surface area of a sphere at

that distance). This power density is called irradiance, a property that can be used

to describe the strength of any emitter of electromagnetic energy.

Fig. 2.1. The effect of the atmosphere in determining various paths for energy to illuminate a

(equivalent ground) pixel and to reach the sensor

2.1 Sources of Radiometric Distortion 29

We can measure a level of solar irradiance at the earth’s surface. If the surface is

perfectly diffuse then this amount is scattered uniformly into the upper hemisphere.

The amount of power density scattered in a particular direction is deﬁned by its

density per solid angle, since equal amounts are scattered into equal cones of solid

angle. This quantity is called radiance and has units of Watts per square metre per

steradian (Wm

−2

−1

The emission of energy by bodies such as the sun is wavelength dependent, as

seen in Fig. 1.4, so that often the term spectral irradiance is used to describe how

much power density is available incrementally across the wavelength range. Spectral

irradiance is typically measured in Wm

−2

µm

−1

As an illustration of how these quantities might be used suppose, in the absence

of atmosphere, the solar spectral irradiance at the earth is E

. If the solar zenith angle

(measured from the normal to the surface) is θ as shown in Fig. 2.1 then the spectral

irradiance (spectral power density) on the earth’s surface is E

cos θ. This gives an

available irradiance between wavelengths λ

and λ



cos θdλ. Wm

−2

In remote sensing the wavebands used (λ = λ

−λ

) are frequently narrow enough

to assume

= E

λ

cos θλ Wm

−2

(2.1)

where E

λ

is the average spectral irradiance in the band λ.

Suppose the surface has a reﬂectance R. This describes what proportion of the

incident energy is reﬂected. If the surface is diffuse then the radiance scattered into

the upper hemisphere and available for measurement is

L = E

λ

cos θλR/π Wm

−2

−1

(2.2)

where the divisor π accounts for the upper hemisphere of solid angle. Knowing L it

is possible to determine the power detected by a sensor, and the digital count value

(or grey level) given in the digital data product from a particular sensor which is

directly related to the radiance of the scene. If we call the digital value (between 0

and 255 for example) C, then the measured radiance of a particular pixel is

L = Ck + L

min

−2

−1

(2.3)

where k = (L

max

− L

min

)/C

max

in which L

max

and L

min

are the maximum and

minimum measurable radiances of the sensor. These are usually available from the

sensor manufacturer or operator.

Equation (2.2) relates to the ideal case of no atmosphere. When an atmosphere is

present there are several mechanism that must be taken into account that modify (2.2).

These are a result of scattering and absorption by the particles in the atmosphere.

Absorption by atmospheric molecules is a selective process that converts incom-

ing energy into heat. In particular, molecules of oxygen, carbon dioxide, ozone and

water attenuate the radiation very strongly in certain wavebands. Sensors commonly

used in solid earth and ocean remote sensing are usually designed to operate away