Реферат - Теорема Піфагора
Подождите немного. Документ загружается.

Тема: теорема Піфагора
«Геометрія володіє двома скарбами: один з них – теорема
Піфагора, а другий – поділ відрізка в середньому і крайньому
відношенні… Перший можна порівняти з мірою золота, а
другий більш нагадує коштовний камінь»
Й. Кеплер
І. Теорема Піфагора.
Теорема Піфагора — основа евклідової геометрії. Завдяки їй
можна довести більшість теорем геометрії. Тому її треба добре
засвоїти. Сьогодні у нас урок однієї теореми, на
якому ви будете знаходити різні способи доведення теореми
Піфагора, використовуючи для цього знання різних розділів
планіметрії; розв'язувати задачі на застосування теореми. У світі
відомо понад 100 різних доведень теореми. Можливо, і ви знайдете
свій оригінальний спосіб доведення, то ж хай вам щастить!
ІІ. Екскурс в історію
Філософські вчення Піфагора мають зараз історичний інтерес,
а наукові відкриття залишаються підвалинами математики, адже
йому належить створення вчення про числа, основи теорії
подібності і доведення того, що сума внутрішніх кутів трикутника
дорівнює двом прямим, доведення теореми, що носить його ім’я.
Відкриття теореми Піфагором оточене ореолом красивих
легенд. Прокл, коментуючи останнє продовження першої книги
“Начал” Евкліда, пише: “Якщо послухати тих, хто повторює давні
легенди, то доводиться сказати, що ця теорема походить від
Піфагора; розповідають, що він у честь цього відкриття приніс у
жертву бик”. Дехто розповідає, що він приніс у жертву не одного
бика, а цілу сотню. На цю тему німецький поет Альберт Шаліссо
написав вірш, який в перекладі Наталіїї Терехової звучить
Во мгле веков пред нашим взором
Блеснула истина. Она,
Как теорема Пифагора,
До наших дней еще верна.
Найдя разгадку, мудрый старец
Был благодарен небесам;
Он сто быков велел зажарить
И в жертву принести богам.
С тех пор быки тревожно дышат,-
Они, кляня дары богов,
О новой истине услышав
Ужасный поднимают рев.
Их старца имя потрясает,
Их истины лучи слепят:
И, новой жертвы ожидая,
Быки, зажмурившись, дрожат.
І хоча ще Цицерон помітив, що будь-яке кровопролиття було
проти закону піфагорійського ордену, легенда ця зрослася з
теоремою Піфагора і через більш ніж 2000 років продовжувала
викликати гарячі відгуки.
Про важливість даної теореми свідчить какий факт: замість
екзамена з математики в середні віки студент повинен був скласти
присягу, що він читав певне число глав з книг «Начала» Евкліда,
написаних в 4 столітті до н.е. В основі всіх сучасних підручників
геометрії лежать положення цих книг. Остання теорема першої
книги називалась «магістр математики». І це була теорема
Піфагора. За знаходження нового доведення цієї теореми в той час
давали вчену ступінь магістра.
На сьогодні існує 370 різних доведень теореми . Їх зібрав і
проаналізував англійський математик Е. Луміс у своїй книзі
«Теореми Піфагора». Але яке з них належить самому вченому не
відомо.
Вперше ми зустрічаємо доведення теореми в «Началах»
Евкліда, але не відомо чи це доведення Піфагора, чи самого автора
книги. Теорема звучала так «В прямокутних трикутниках
квадрат на стороні, що стягує прямий кут, дорівнює разом
узятим квадратам на сторонах, що утворюють прямий кут»
Покажемо це доведення:
ІІІ. Доведення теореми
Піфагора
Доведення №1 (за
Евклідом)
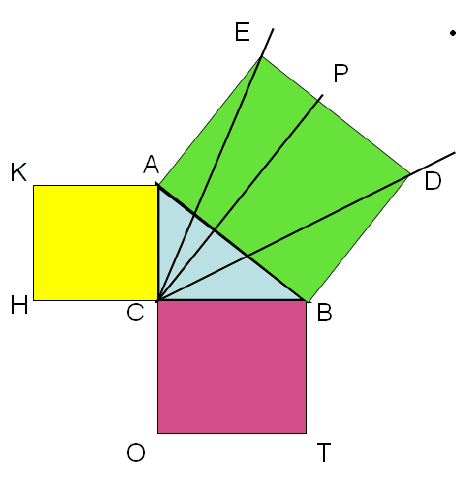
На сторонах прямокутного
трикутника АВС побудовані
квадрати AEDB, ACHK,
CBTO. Проведемо відрізок СР
параллельно до сторін
більшого
квадрата АЕ і BD, а також
прямі CE, CD, KB, AT . ∆AEC
= ∆ABK за двома сторонами
і кутом між ними (AK=AC,
AB=AE, KAB=CAE як такі, що складаються з прамих кутів і
спільного для них кута CAB).
Площа ∆АЕС дорівнює половині площі прямокутника АЕРМ,
оскільки в них спільна основа АЕ і рівні висоти. Площа
трикутника АВК дорівнює половині площі квадрата АСНК( у них
також спільна основа і рівні висоти). Таким чином ми одержали, що
квадрат АСНК рівновеликий прямокутнику АЕРМ.
Аналогічно доводимо рівність трикутників CDB і АВТ і
відповідно рівновеликість квадрата СВТО і прямокутника MPDB.
На завершення отримуємо, що сума площ квадратів АСНК і СВТО
рівна площі квадрата AEDB. Якщо позначити катети прямокутного
трикутника a і b, а гіпотенузу с, то отримаємо відоме
співвідношення між сторонами a
2
+ b
2
= с
2
Теорема Піфагора чудова тим, що сама по собі вона не
очевидна. Наприклад, властивості рівнобедреного кутника можна
бачити безпосередньо на малюнку. А скільки не дивися на
прямокутний трикутник, ніяк не збагнеш, що між його сторонами є
таке просте співвідношення a
2
+ b
2
= с
2
Це співвідношення стає
очевидним, якщо вдало побудувати малюнок. В цьому і є суть
геометрії: за допомогою побудови зробити неочевидне очевидним.
В математичних трактатах Древньої Індії, доводячи теорему, часто
наводили тільки рисунок. Супроводжували його лише одним
словом: «Дивись!»
Давайтевайте і ми подивимось і доведемо теорему Піфагора.

Доведення №2 («Дивись»)
Очевидно факт, викладений в
теоремі Піфагора був спочатку
встановлений для рівнобедреного
прямокутного трикутника. Достатньо
поглянути на мозаїку, щоб
переконатися в справедливості
теореми для трикутника АВС.
Для доведення загального випадку
в Древній Індії використовували
декілька способів:
В квадраті зі стороною a+b зображали чотири прямокутних
трикутники з катетами a і b і писали «Дивись». І дійсно,
поглянувши на ці малюнки, бачимо, що зліва вільна від
трикутників фігура, складається з двох квадратів зі сторонами a і b і
відповідно її площа
a
2
+ b
2,
а справа квадрат зі стороною с. Його площа с
2
. Маємо
рівність a
2
+ b
2
= с
2
Покладемо індійське доведення на математичну основу
Доведення №3 (індійське доведення)
Площа великого квадрата S
в. квадрата =
с
2
S
в. квадрата =
4S
трикутника
+S
м. квадрата
S
в. квадрата =
4 ½ ab + (a-b)
2
2ab + a
2 –
2ab+ b
2
= с
2
a
2
+ b
2
= с
2
Доведення №4 (за допомогою тригонометричних функцій)
COSA =b
c
/b = b/c
COSB =a
c
/a = a/c
b
2
=c b
c
; a
2
=aa
c
;
a
2
+ b
2
= с(a
c +
b
c
) = c
2
Доведення №5 (методом координат).
Введемо систему координат: катети трикутника лежать на осях,
початок координат у вершині прямого кута. Тоді А(0;а), В(в; 0),
С(0; 0).
Знайдемо відстані АВ, АС, ВС:
АВ
2
= (в - 0)
2
+ (0-а)
2
= в
2
+ а
2
,
АС
2
= (0 - 0)
2
+ (0-а)
2
= а
2
,
ВС
2
= (в – 0)
2
+ (0 – 0)
2
= в
2
, звідси
АВ
2
= АС
2
+ ВС
2
.
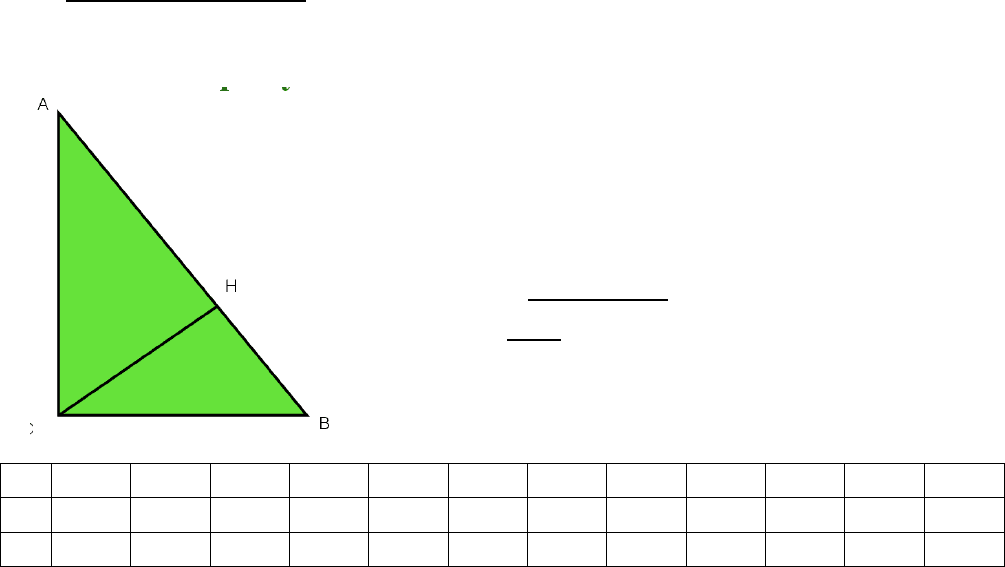
Доведення №6 (через подібність трикутників)
∆ ABC ∆ ACH, тому АС/АВ = АН/
АС, АС
2
=АВАН
∆ ABC ∆ СВH, тому ВС/АВ = ВН/
ВС, ВС
2
=АВВН
Звідси АС
2 +
ВС
2
= АВ (АН +ВН) =
АВАВ = АВ
2
А 3 5 8 7 20 12 9 28 11 16 33 48
В 4 12 15 24 21 35 40 45 60 63 56 55
С 5 13 17 25 29 37 41 53 61 65 65 73
Сьогодні теорема Піфагора виявлена у різних часткових
задачах та кресленнях: і в єгипетському трикутнику в папірусі часів
фараона Аменемхета першого (біля 2000р. до н. е.), і у
вавилонських клинописних табличках епохи царя Хаммурапі
(XVIII ст. до н. е.), і в давньоіндійському трактаті VII-V ст. до н. е.
“Сульва сутра”. У найдавнішому китайському трактаті “Чжоу-бі
суань цзинь” час створення якого точно не відомо, стверджується,
що в XII ст. до н. е. Китайці знали властивості єгипетьського
трикутника, а до VI ст. до н. е.- й загальний вигляд теореми. Цікаво,
що саме такі пропорції археологи знаходять у розмірах тесаних
плит піраміди Хефрена. Про цілочислові прямокутні трикутники
знали ще в стародавньому Вавілоні 3 тисячі років до н.е. Було
складено табличку, за якою шукали сторони таких трикутників.

Не дивлячись на це, ім’я Піфагора щільно злилося з теоремою
Піфагора. Сьогодні прийнято вважати, що Піфагор першим довів
теорему, яка носить його ім’я. На жаль, його доказ не дійшов до
нашого часу.
IV. Закріплення вивченого матеріалу. Використання
теореми Піфагора на практиці
Готуючись до сьогоднішнього семінару ви опрацювали багато
літератури і легко зможете відповісти на такі запитання
Запитання
1. Про яке число єгиптяни говорили, що воно має
божественну властивість і чому?
Число 5, бо його квадрат дорівнює сумі квадратів двох
попередніх чисел
2. У піфагорійців самою страшною клятвою вважалась
клятва числом … Чому?
36: дорівнює сумі перших чотирьох парних і перших чотирьох
непарних чисел; сумі кубів трьох перших натуральних чисел
3. Яке відкриття в школі Піфагора призвело до першої
кризи в математиці?
Несумісність сторони квадрата і його діагоналі ( не кожен
відрізок має довжину, що вимірюється цілим числом)
4. Чи можна побудувати прямокутний трикутник, у
якого всі сторони є непарними числами?
Ні, сума квадратів двох непарних чисел є число парне
5. Які числа називають піфагоровими?
трійки натуральних чисел, що мають властивість a
2
+ b
2
= с
2
6. Чи можна з 36 сірників, не ламаючи їх скласти
прямокутний трикутник?
Можна, 3n +4n +5n =36
7. Як за допомогою теореми Піфагора можна
геометрично знаходити квадратні корені з цілих чисел?
8. Є мотузка, поділена вузликами на 12 рівних частин
Для чого використовувалася така мотузка в Древньому Єгипті
( для побудови прямих кутів)
9. Що, в перекладі з грецької означають терміни:
гіпотенуза, катет?
Гіпотенуза – та, що стягує
Катет – перпендикуляр, відвіс
10. Що піфагорійці називали «віслюковим мостом»?
Теорему Піфагора. Вважали, що той, хто її не розуміє, «не
пройде через неї» – справжній віслюк.
11. Якось Піфагора запитали: «Скільки учнів навчається
у тебе в школі?». Він відповів: «Половина вивчає математику,
четверта частина – музику, сьома – мовчить і ще є три жінки»
( 28 учнів)
V. Підсумок семінару
На сьогоднішньому уроці ми з вами мали змогу переконатися у
тому, що теорема Піфагора є одним із найважливіших
геометричних тверджень і відіграє основну воль у геометричних
обчисленнях.
Важливість теореми Піфагора підтверджує і такий факт.
Наприкінці 19 століття було відкрито на Марсі канали, які тривалий
час вважалися штучними. Для налагодження зв’язків з марсіанами
запропонували на величезному просторі Західно-Сибірської низини
побудувати велетенську фігуру, яка б світилася – рисунок теореми
Піфагора, бо вважали, що ця теорема справедлива скрізь.
Іншопланетяни, повинні зрозуміти такий сигнал, зробити висновок,
що на Землі живуть розумні істоти і відповісти мовою математики,
адже її вважають універсальною мовою Всесвіту.
Ось чому люди пам 'ятають Піфагора дві з половиною тисячі
років. Ось чому серед знаменитих олімпійських чемпіонів він довго
залишиться найвідомішим, тому що йому випало щастя перемогти
не тільки супротивників, але й перемогти час.
