Реферат - Метод анализа иерархий
Подождите немного. Документ загружается.

Собственные векторы и значения матриц
Ранжирование элементов, анализируемых с использованием матрицы
парных сравнений [E], осуществляется на основании главных собственных
векторов, получаемых в результате обработки матриц.
Вычисление главного собственного вектора W положительной
квадратной матрицы [E] проводится на основании равенства:
EW=λ
max
W, (1)
где λ
max
— максимальное собственное значение матрицы [Е].
Для положительной квадратной матрицы [Е] правый собственный
вектор W, соответствующий максимальному собственному значению λ
max
, с
точностью до постоянного сомножителя С можно вычислить по формуле:
,lim CW
eEe
eE
k
T
k
k
(2)
где е={1,1,1, ....l}
Т
– единичный вектор;
k = 1, 2, 3, ... — показатель степени;
С— константа;
Т — знак транспонирования.
Вычисления собственного вектора W по выражению (2) производятся
до достижения заданной точности:
,
)1(
k
llT
WWe
(3)
где l — номер итерации, такой, что l = 1 соответствует k = 1; l = 2,
k = 2;
l = 3, k = 4 и т. д.;
— допустимая погрешность.
С достаточной для практики точностью можно принять
= 0,01
независимо от порядка матрицы.
Максимальное собственное значение вычисляется по формуле:
λ
max
=e
T
[E]W
21

На практике для расчета собственного вектора W также применяется
приближенный метод среднегеометрического, вычисляемое по следующему
соотношению:
W
i
=
n
inii
aaa
21
(4)
где a
ij
— агрегированная оценка элемента, принадлежащего i-й строке и
j-му столбцу матрицы парных сравнений;
n— число элементов.
Оценка однородности суждений
В практических задачах количественная (кардинальная) и транзитивная
(порядковая) однородность (согласованность) нарушается, поскольку
человеческие ощущения нельзя выразить точной формулой. Для улучшения
однородности в числовых суждениях, какая бы величина aij ни была взята
для сравнения i-го элемента с j-м, a
ij
приписывается значение обратной
величины, т. е. а
ij
= 1/a
ij
. Отсюда следует, что если один элемент в а раз
предпочтительнее другого, то последний только в 1/а раз предпочтительнее
первого.
При нарушении однородности ранг матрицы отличен от единицы и она
будет иметь несколько собственных значений. Однако при небольших
отклонениях суждений от однородности одно из собственных значений будет
существенно больше остальных и приблизительно равно порядку матрицы.
Таким образом, для оценки однородности суждений эксперта необходимо
использовать отклонение величины максимального собственного значения
λ
max
от порядка матрицы п.
Однородность суждений оценивается индексом однородности (ИО) или
отношением однородности (OO) в соответствии со следующими
выражениями:
)(/
;1
max
ИОМИОOO
nnИО
22
где: М(ИО) — среднее значение (математическое ожидание) индекса
однородности случайным образом составленной матрицы парных сравнений
[E], которое основано на экспериментальных данных, полученных в работе
Сакман Г. «Решение задач в системе человек».
В качестве допустимого используется значение OO ≤ 0,10. Если для
матрицы парных сравнений отношение однородности OO > 0,10, то это
свидетельствует о существенном нарушении логичности суждений,
допущенном экспертом при заполнении матрицы, поэтому эксперту
предлагается пересмотреть данные, использованные для построения
матрицы, чтобы улучшить однородность.
ПРИМЕР: Оценка однородности - это метод позволяющий выявить
математическими методами те места, где человек сравнивающий
альтернативы (критерии) противоречит себе. Например выставлена такая
матрица сравнения альтернатив
1 3 5
1/3 1 1/9
1/5 9 1
Здесь можно человеческим глазом увидеть, что сравнивая эти
альтернативы эксперт говорит "первой строкой" - что вторая должна быть
более предпочтительнее третья, но "второй строкой" - указывая 1/9
утверждает что вторая хуже третьей в 9 раз.
Метод однородного суждения применим для любого объема матриц,
кроме того возможно реализовать и на ЭВМ.
Пример решения задачи многокритериального выбора на
иерархиях с различным числом и составом альтернатив под
критериями.
В практике принятия решений нередко встречается задача, когда
ранжируемые по множеству критериев альтернативы оцениваются экспертом
не по всем критериям. Эта задача характерна для ситуаций, в которых
множество критериев, выделенных для всех рассматриваемых альтернатив,
является избыточным относительно одной или нескольких альтернатив.
23
Таким образом, в рассматриваемом случае эксперт имеет разное количество
альтернатив под каждым критерием или под их частью.
Рассмотрим методику определения вектора приоритета альтернатив
для случая, когда иерархия имеет один уровень критериев, объединенных
фокусом с учетом значимости критериев, и разное количество альтернатив у
каждого критерия. Методика предполагает выполнение ряда этапов по
структурированию информации и проведению вычислительных операций.
Постановка задачи.
Перед ЛПР стоит задача - израсходовать определенную сумму. Для
наглядности считается, что ЛПР расходует средства разово без возможности
ее поделить и использовать сразу в нескольких проектах. Основной целью
(фокусом) расходования средств является получения экономической и
политической выгоды для ЛПР.
Выделим следующие критерии:
1) Получение максимальной выгоды в будущем от вложения финансов
для ЛПР;
2) Получение политических «очков» в конкретном городе.
Перед ним стоят следующие альтернативы:
1) Инвестирование в автомобильный завод (основной работодатель
города)
2) Открытие сети аптек;
3) Положить деньги на депозит в западные банки;
4) Финансирование детского дома;
5) Оплата PR-акции.
Для наглядности альтернатива 3 нельзя оценить с точки зрения
политической выгоды, аналогично альтернативы 4 и 5 не оцениваются
экспертом с точки зрения экономической выгоды для ЛПР.
24
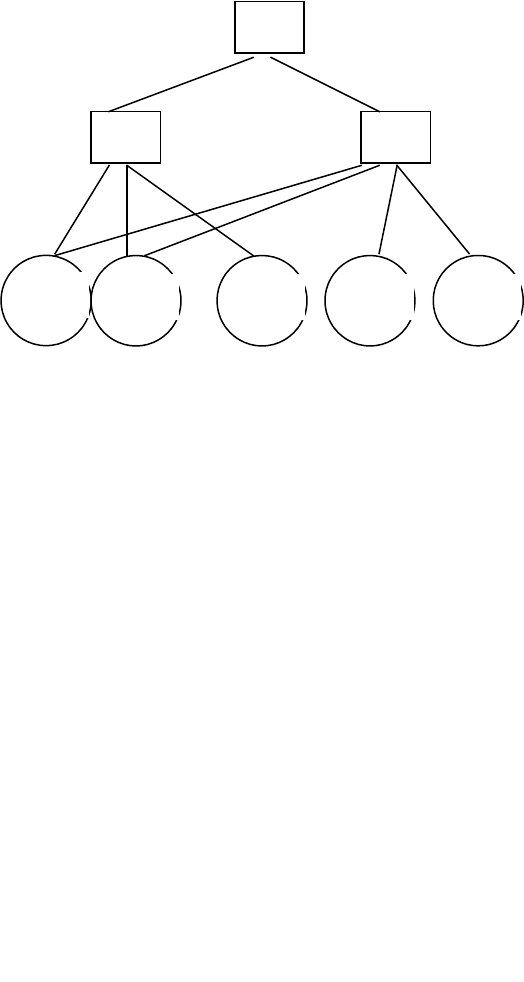
Этап №1. Построение иерархии.
Исходная проблема структурируется в виде иерархии,
устанавливающей взаимосвязь между множеством сравниваемых
альтернатив {А
i
}и множеством критериев {E
k
i
}.
Рис. 2. Иерархия поставленной задачи.
Альтернативы А
4
и А
5
не оцениваются по критерию E
2
1
, а альтернатива
А
3
- по критерию E
2
2
согласно условию задачи.
Этап №2.
На основе иерархической структуры определяется бинарная матрица
[В], устанавливающая соответствие между альтернативами и критериями.
Матрица [В] содержит элементы bij = {0,1}. При этом если альтернатива Аi
оценивается по критерию Ej, то bij = 1, в противном случае bij = 0.
10
10
01
11
11
2
2
2
1
5
4
3
2
1
EE
A
A
A
A
A
B
Этап №3. Попарное сравнение критериев
Осуществляется экспертная оценка критериев по соответствующим
критериям. Для этой цели используются метод попарного сравнения, метод
сравнения относительно стандартов или метод копирования.
Попарное сравнение критериев относительно друг друга см. табл. 1.:
25
1
1
E
2
2
E
2
1
E
1
A
2
A
3
A
4
A
5
A
Таблица 2.Попарное сравнение критериев
m E
2
1
E
2
2
W-главный
собственный
вектор
Вес критерия
нормированный (
X
)
E
2
1
1 5 2,24 0,83
E
2
2
1/5 1 0,45 0,17
W-главный собственный вектор вычисляется по формуле:
n
n
j
ji
A
1
,
2
i
W
, где n – размерность таблицы
,2425*1W
2
2
1
0,451*5/1W
2
2
2
Необходимо произвести нормирование собственного вектора по
формуле:
ji
n
i
ji
W
W
критерияВесныйНормирован
,
1
,
__
Следовательно, нормированный вес критерия:
0,832,24/2,69X
1
0,170,45/2,69X
2
Этап №4. Попарное сравнение альтернатив
Аналогичным образом рассчитывались матрицы попарного сравнения
альтернатив в соответствии с каждым критерием на 2 уровне иерархии.
Таблица 2. Попарное сравнение альтернатив для критериев 1.
m А
1
А
2
А
3
W-главный
собственный вектор
Вес нормированный
(W
н
)
А
1
1 3
5
2,47 0,72
А
2
1/3 1
2
0,87 0,25
А
3
1/5 1/2
1
0,1 0,03
Таблица 2. Попарное сравнение альтернатив для критериев 2.
m А
1
А
2
W-главный
собственный
Вес нормированный
(W
н
)
26

А
4
А
5
вектор
А
1
1 3 1/3 1/4 0,25 0,00325
А
2
1/3 1 1/5 1/6 0,01 0,00013
А
4
3 5 1 1/3 5 0,06
А
5
4 6 3 1 72 0,936
На основе экспертных оценок с учетом матрицы [В] строится матрица
[А] следующего вида:
936,00
06,00
003,0
00013,025,0
00325,072,0
2
2
2
1
5
4
3
2
1
EE
A
A
A
A
A
A
Этап №5. Формируются структурные критерии S и L,
отображаемые соответствующими диагональными матрицами [S] и [L].
Рассмотрим состав упомянутых матриц.
Матрица [S] имеет следующий вид:
10
01
0
0
2
2
2
1
1
1
2
1
1
1
2
2
2
1
EE
a
a
EE
S
r
i
j
r
i
j
где aij — значения векторов приоритетов из матрицы [А].
С помощью матрицы [S] обеспечивается нормирование векторов
приоритетов альтернатив, образующих матрицу [А], если последняя
заполнена методом сравнения относительно стандартов или копирования без
предварительного нормирования. Но т.к. вектора уже были нормированы на
4 этапе нормированы, то [S]- единичная.
Матрица [L] имеет следующий вид:
27

5
4
0
0
5
3
0
0
2
2
2
1
1
1
2
2
2
1
EE
N
R
N
R
EE
L
где Rj — число альтернатив Аi, находящихся под критерием Еj,
N — суммарное число альтернатив, находящихся под всеми
критериями.
Здесь следует отметить, что число N в матрице [L] может приниматься
равным числу рассматриваемых альтернатив r, т.е. N= r. При этом на
конечный результат способ определения N не оказывает влияния.
Использование структурного критерия L позволяет эксперту или ЛПР
изменять при необходимости вес альтернатив, связанных с
соответствующими критериями пропорционально отношению Rj / N. Этим
обеспечивается повышение приоритета альтернатив, образующих большие
группы, и снижение приоритета альтернатив в группах с их относительно
небольшим числом. Здесь имеется в виду, что группу определяют
альтернативы, являющиеся "потомками" по отношению к критерию Ej.
Необходимость в приведенной вычислительной процедуре обусловлена тем,
что у критериев-"родителей" с высоким приоритетом в иерархии может
находиться большое число альтернатив-"потомков", а у критериев-
родителей" с низким приоритетом — значительно меньшее число
альтернатив-"потомков", чем в первом случае. Поэтому в этой ситуации
желательно повышение приоритетов альтернатив в большой группе,
поскольку, если альтернатив много, каждая из них получит меньший
составной приоритет, чем каждая альтернатива, входящая в меньшую группу
с низким приоритетом критерия.
28

Этап №6.
Определяется вектор приоритетов альтернатив W относительно
критериев. Данная процедура реализуется последовательным
перемножением слева направо следующих матриц и векторов:
а) для случая, когда экспертные оценки в матрице [А] ненормированы:
XLSAW
;
б) для случая, когда экспертные оценки в матрице [А] нормированы:
XLAW
Т.к. у нас матрица [А] нормирована воспользуемся второй формулой.
0,12733
0,00816
0,01494
0,124517
0,359002
17,0
83,0
0,7490
0,0480
00,018
0,00010,15
0,00260,432
17,0
83,0
5
4
0
0
5
3
936,00
06,00
003,0
00013,025,0
00325,072,0
W
Для окончательного нормирования используется диагональная
матрица [В]. Эта матрица имеет следующий вид:
29
1,5770000
01,577000
001,57700
0001,5770
00001,577
0000
0000
0000
0000
0000
1
5
1
1
5
1
1
5
1
1
5
1
1
5
1
i
i
i
i
i
i
i
i
i
i
x
x
x
x
x
B
где х
i
— значение ненормированного вектора приоритетов альтернатив,
полученное после последовательного перемножения слева направо матриц
XLSAW
;
В итоге получаем, следующий нормированный вектор приоритетов
альтернатив W.
0,1999081
0,01286832
0,02356038
90,19636330
40,56614615
W
Согласно полученному результату для наилучшего удовлетворения
основного критерия необходимо выбрать альтернативу А
1
(«Инвестирование
в автомобильный завод»), т.к. она имеет наивысший рейтинг 0,566146145.
Этап №7. Оценка согласованности.
Весьма полезным побочным продуктом теории является так
называемый индекс согласованности (ИС), который дает информацию о
степени нарушения численной и транзитивной (порядковой)
согласованности. Для улучшения согласованности можно рекомендовать
30
